конспект лекций Ф1 (1). Лекция 1 Кинематика План
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Лекция 1 Кинематика —План 1. Кинематическое описание движения материальной точки. 2. Скорость. 3. Ускорение. 4. Угловая скорость. 5. Угловое ускорение. Обычно для описания движения тел используют декартовую систему координат. В декартовой системе координат положение материальной точки М задается координатами x, y, z или радиус-вектором Радиус-вектор– это вектор, проведенный из начала координат в данное положение материальной точки. При движении материальной точки ее координаты x, y, z и радиус-вектор 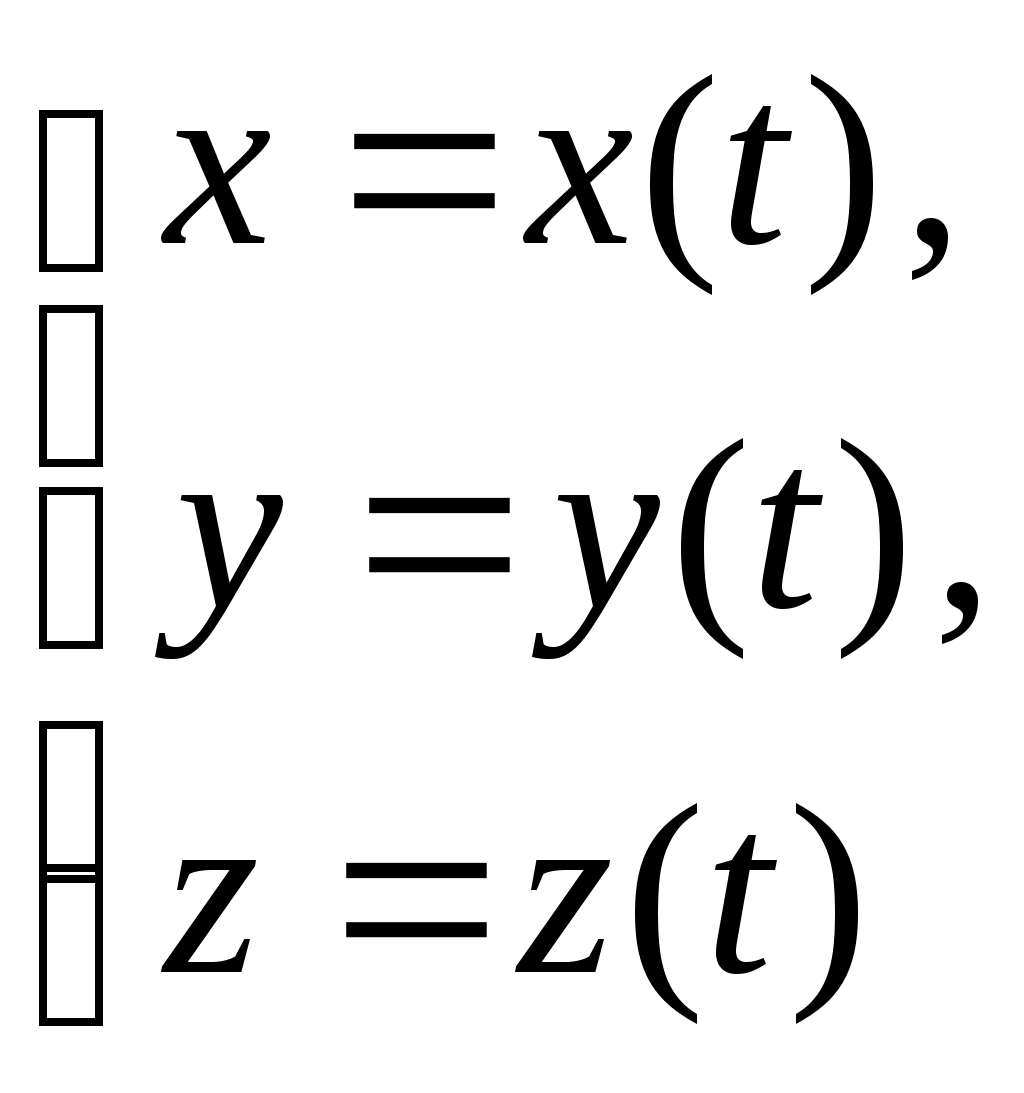 или одним векторным уравнением Эти уравнения называются кинематическими уравнениями движения материальной точки. Скорость – это производная радиус-вектора по времени: Скоростьчисленно равна производной пути во времени и направлена по касательной к траектории в той точке, где находится частица в данный момент времени, в сторону движения. Средним ускорением в промежутке времени Dt = t2– t1 называется вектор, равный отношению приращения скорости к промежутку времени Dt: Вектор среднего ускорения совпадает по направлению с вектором приращения скорости. Ускорение – это первая производная скорости по времени или вторая производная радиус-вектора по времени: Тангенциальное ускорение характеризует быстроту изменения скорости по модулю, направлено по касательной к траектории и равно аt = u¢. Нормальное ускорение характеризует быстроту изменения скорости по направлению, направлено по нормали к траектории к центру ее кривизныи равно Векторы 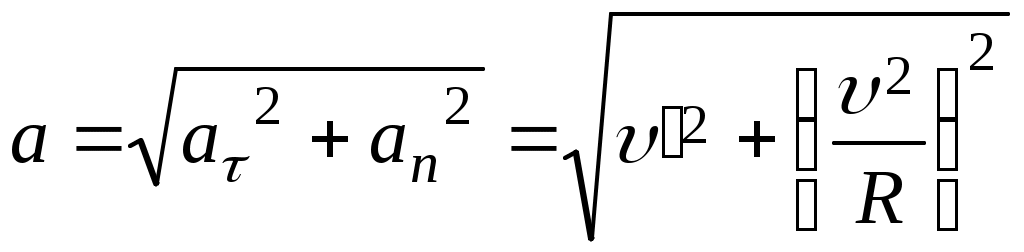 . .Вращательным движением абсолютно твердого тела называется движение, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Модуль угловой скорости определяется выражением где Dj – угол, на который поворачивается тело за время Dt. Угловая скорость численно равна первой производной угла поворота по времени. Угловая скорость – векторная величина. Она направлена вдоль оси вращения в сторону, определяемую правилом правого винта (буравчика). Угловое ускорение Угловое ускорение – это первая производная угловой скорости по времени. Вектор Контрольные задания для СРС (Лекция 1) [1,2,3,4] 1. Предмет физики. Методы физического исследования: опыт, гипотеза, эксперимент, теория. Основные единицы СИ. 2. Понятие материальной точки, абсолютно твердого тела. 3. Система отсчета. Траектория, путь, перемещение. 4. Равномерное движение. Равнопеременное движение. 5. Связь между линейными и угловыми величинами. Лекция 2 Динамика —План Преобразования Галилея. Механический принцип относительности. Неинерциальные системы отсчета. Момент силы. Момент импульса. Момент инерции. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Преобразования Галилея 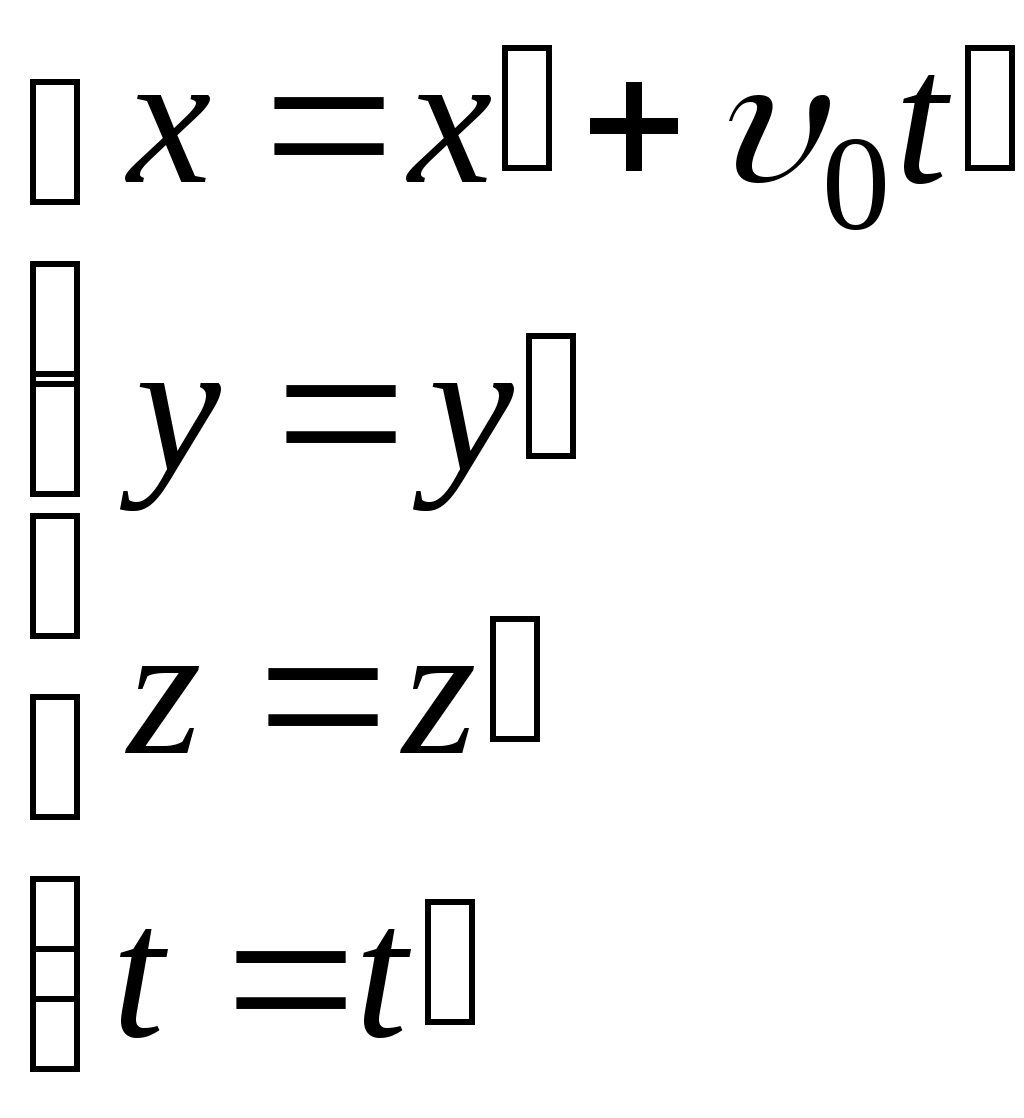 и и 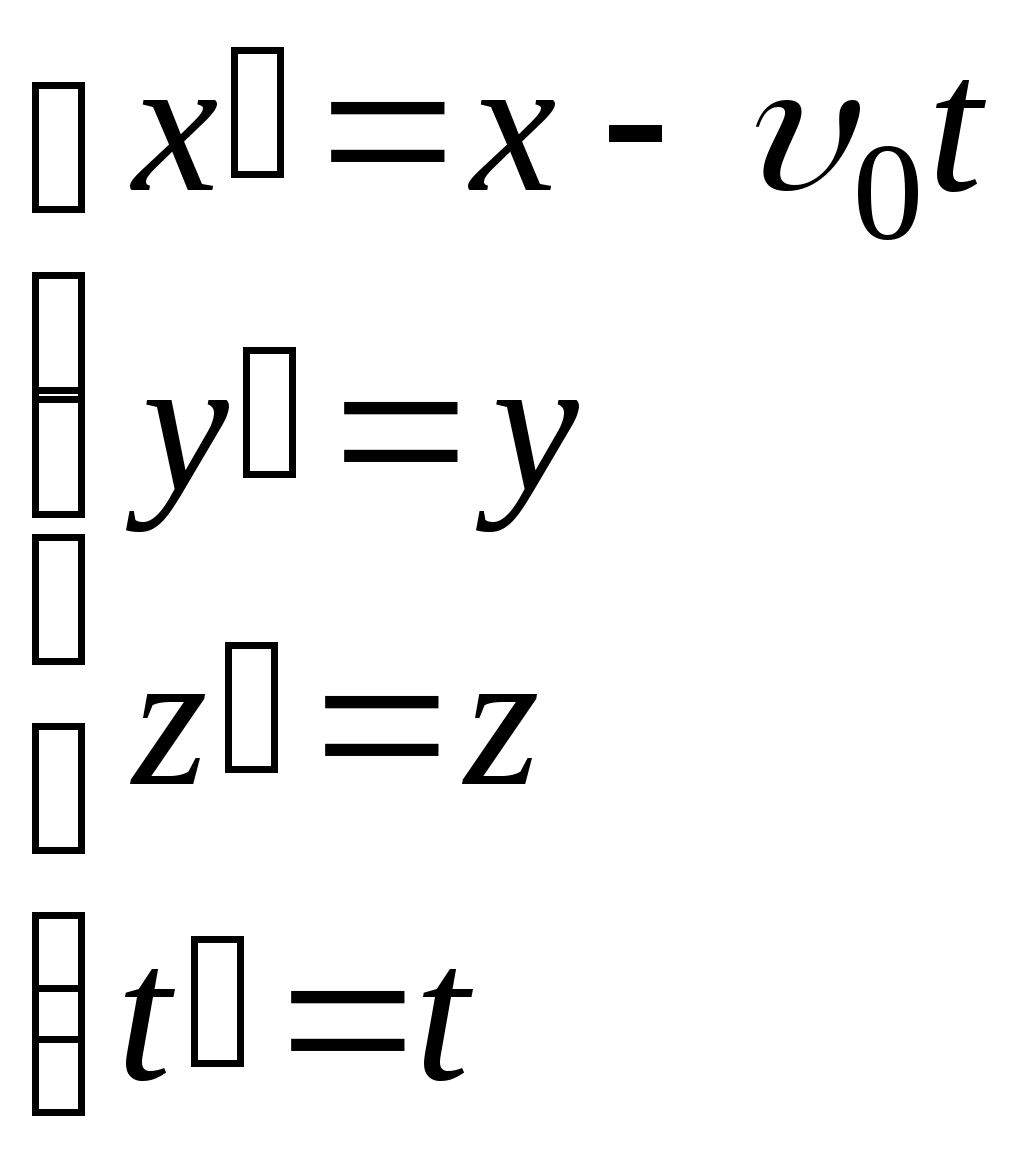 позволяют перейти от координат и времени одной инерциальной системы отсчета к координатам и времени другой инерциальной системы. Механический принцип относительности: законы механики имеют одинаковый вид во всех инерциальных системах отсчета. Величины, имеющие одинаковое числовое значение во всех инерциальных системах отсчета, называются инвариантными (от латинского слова "неизменяющийся"). Если при переходе от одной инерциальной системы отсчета к другой вид уравнений не меняется, то такие уравнения называются инвариантными, т.е. не изменяющимися по отношению к преобразованиям координат и времени. Уравнения механики инвариантны по отношению к преобразованиям Галилея. Система отсчета, которая движется относительно инерциальной системы отсчета с ускорением, является неинерциальной. Сила инерции где Сила инерции возникает в неинерциальных сисЛекциях отсчета за счет ускоренного движения системы. Введение сил инерции позволяет описывать движение тел и в инерциальных и в неинерциальных сисЛекциях отсчета одинаковыми уравнениями. Моментом силы где M = Frsin = Fl, где – угол между векторами Проекция вектора Моментом импульса частицы относительно точки О называется вектор где Проекция вектора Момент инерции является мерой инертности тела во вращательном движении и характеризует способность тела сохранять свою угловую скорость. Момент инерции зависит от формы, размеров тела, распределения массы относительно оси вращения и выбора оси вращения. Момент инерции материальной точки I =mR2, гдеR – расстояние от точки до оси вращения. Момент инерции произвольного тела Уравнение динамики вращательного движения твердого тела относительно неподвижной оси I = Mz . Контрольные задания для СРС (Лекция 2) [1,2,3,4] 1. Первый закон Ньютона. Инерциальные системы отсчета. 2. Масса. Сила. 3. Виды сил в механике. 4. Второй закон Ньютона. Третий закон Ньютона. 5. Моменты инерции тел простейшей геометрической формы. Теорема Штейнера. Лекция 3 Законы сохранения — План Кинетическая энергия. Потенциальная энергия. Консервативные силы. Поле центральных сил. Закон сохранения механической энергии. Закон сохранения момента импульса. Энергияявляется универсальной количественной мерой различных форм движения и взаимодействия. Величина называется кинетической энергией частицы. Кинетическая энергия определяется массами и скоростями рассматриваемых тел и зависит от выбора системы отсчета. Работа результирующей всех сил, действующих на частицу, идет на приращение ее кинетической энергии A = Ek2 – Ek1. Потенциальная энергия определяется взаимным расположением тел или частей тела и их взаимодействием друг с другом. Потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Потенциальную энергию в каком-то определенном положении считают равной нулю, т.е. выбирают нулевой уровень отсчета, а энергию в других положениях отсчитывают относительно этого нулевого уровня. Потенциальная энергия тела в поле сил тяжести Ep = mgh, где h – высота тела над нулевым уровнем, для которого Ep0 = 0. Обычно за нулевой уровень отсчета выбирают поверхность Земли. Силы, работа которых при перемещении тела из одного положения в другое не зависит от формы траектории, а зависит только от начального и конечного положений тела, называется консервативными. В механике к консервативным силам относятся гравитационные силы (силы тяжести) и силы упругости. Работа консервативных сил совершается за счет убыли потенциальной энергии и равна приращению потенциальной энергии со знаком "–": А = Ep1 – Ep2 = –DEp . Консервативная сила равна градиенту потенциальной энергии тела, взятому с обратным знаком К неконсервативным силам относятся силы трения и силы сопротивления среды. Поле, в каждой точке которого направление силы, действующей на тело, проходит через неподвижный центр, а величина этой силы зависит только от расстояния r до этого центра F = F(r), называется центральным. Направлена сила к центру или от центра. Поле гравитационных сил является центральным. Для характеристики гравитационного поля вводятся напряженность и потенциал. Напряженность гравитационного поля – это силовая характеристика поля Потенциал гравитационного поля – это энергетическая характеристика поля Связь между напряженностью и потенциалом Закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной Е = const . Этот закон связан с однородностью времени, т.е. равнозначностью всех моментов времени. При наличии неконсервативных сил приращение полной механической энергии равно работе неконсервативных сил Е2 – Е1 =Анеконс. Закон сохранения момента импульса: момент импульса замкнутой системы тел остается постоянным. Этот закон связан с изотропностью пространства, т.е. одинаковостью свойств пространства по всем направлениям. Контрольные задания для СРС (Лекция 3) [1,2,3,4] 1. Закон сохранения импульса. 2. Центр масс механической системы и закон его движения. 3. Работа. Мощность. Лекция 4 Элементы специальной теории относительности — План 1. Постулаты Эйнштейна. 2. Преобразования Лоренца. Следствия из преобразований Лоренца. 3. Интервал между событиями. 4. Релятивистский закон сложения скоростей. 5. Релятивистская динамика. В основе специальной теории относительности лежат два постулата Эйнштейна: 1) принцип относительности Эйнштейна – все законы природы имеют одинаковый вид во всех инерциальных сисЛекциях отсчета; 2) принцип постоянства скорости света – скорость света в вакууме не зависит от движения источника света и одинакова во всех инерциальных сисЛекциях отсчета. Скорость света в вакууме является предельной. Существование предельной скорости приводит к тому, что время в разных инерциальных сисЛекциях отсчета течет неодинаково. Релятивистскими называются эффекты, которые наблюдаются при движении тел со скоростями близкими к скорости света. Рассмотрим две инерциальные системы отсчета K (x, y, z) и K (x¢, y¢, z¢). Система отсчета Kнеподвижна. Система отсчета K¢ движется относительно K с постоянной скоростью Преобразования Лоренца 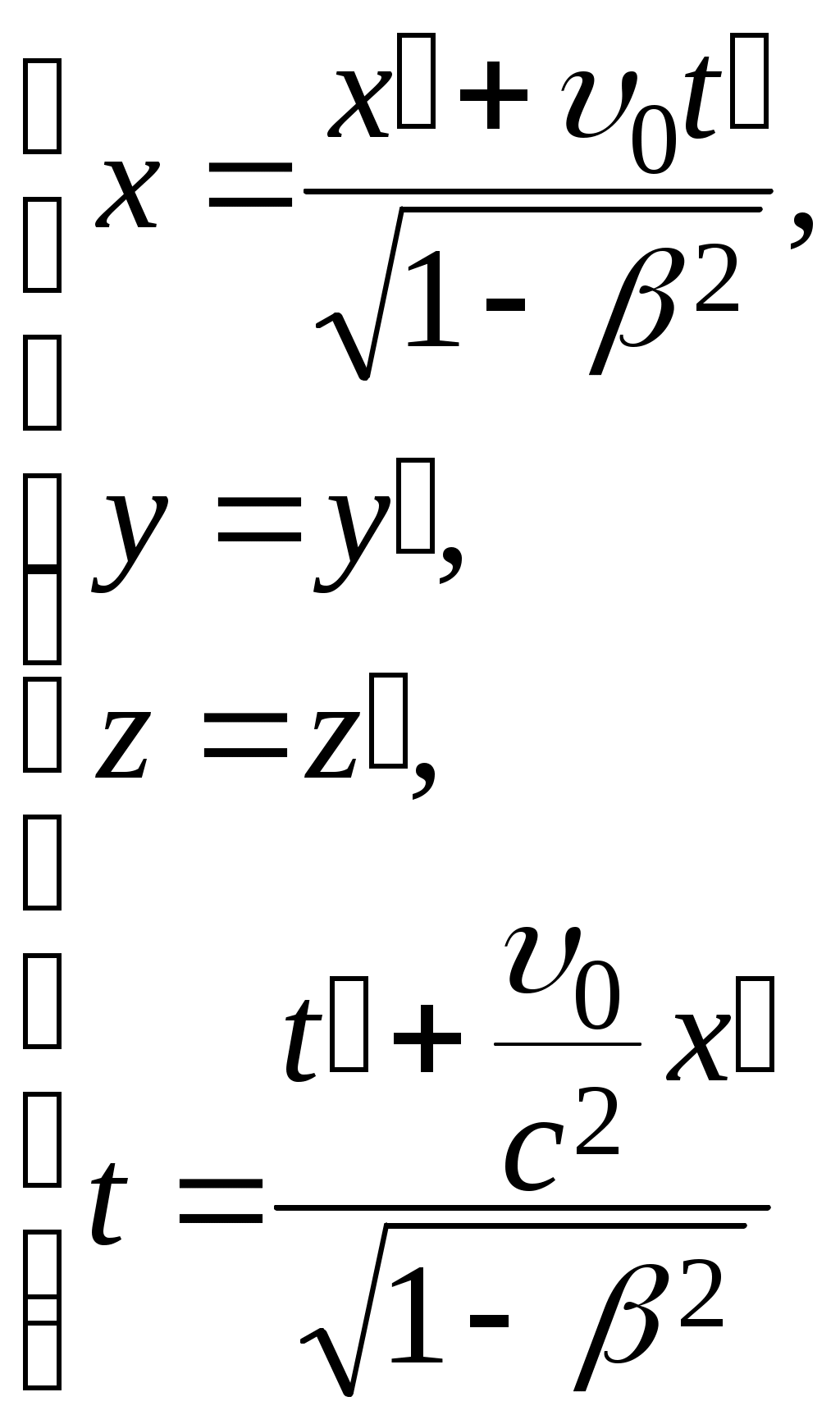 и и 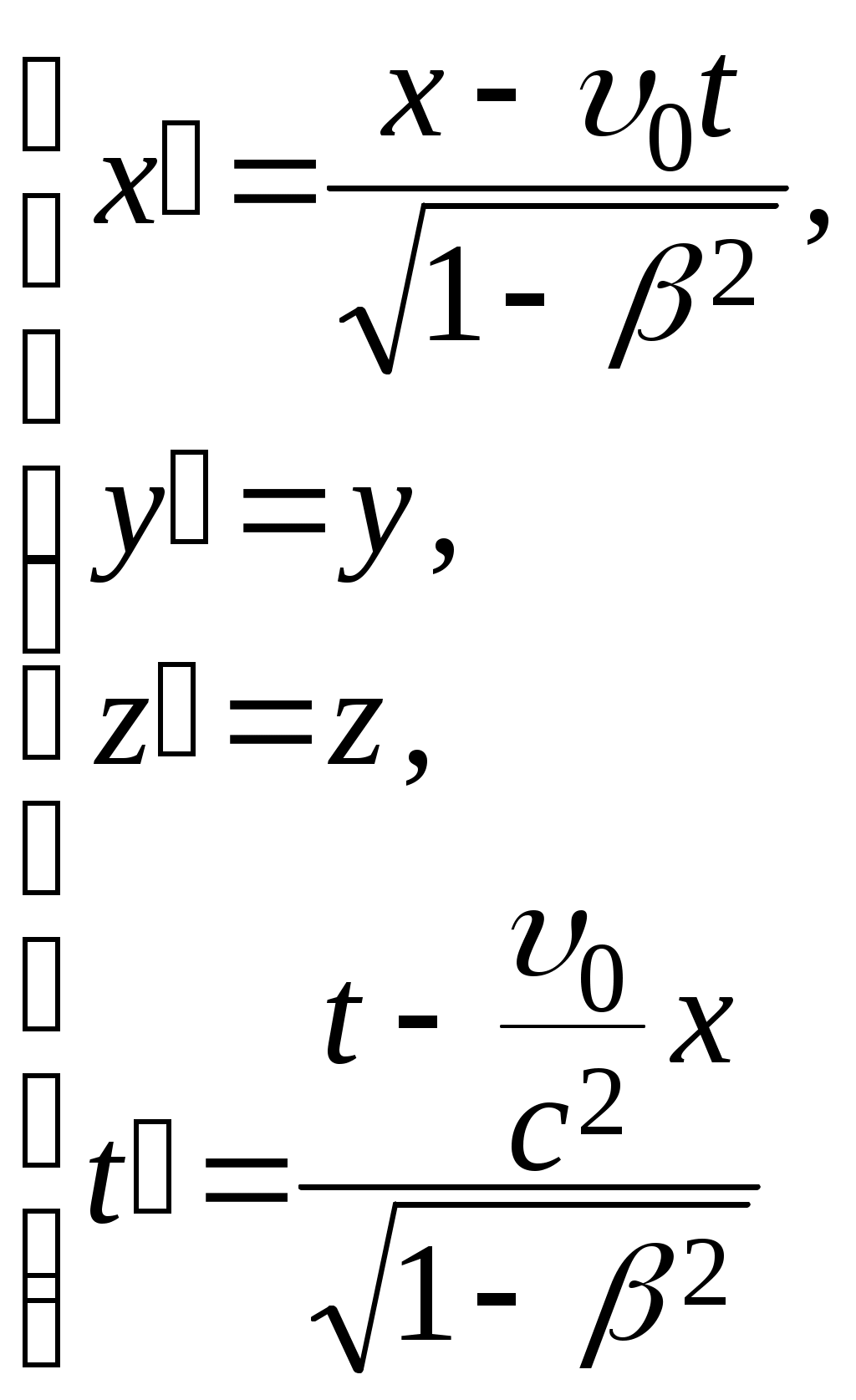 позволяют перейти от координат и времени одной инерциальной системы отсчета к координатам и времени другой инерциальной системы. При 0 << с ( Следствия из преобразований Лоренца: 1) относительность одновременности. События, одновременные в одной системе отсчета, неодновременны в другой. 2) длина тел в разных системах отсчета. Длина стержня l, измеренная в системе отсчета, относительно которой он движется, меньше длины l0, измеренной в системе отсчета, относительно которой он покоится. Линейные размеры тела сокращаются в направлении движения тем больше, чем больше скорость движения тела. 3) промежуток времени между событиями. Часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов. Из преобразований Лоренца следует, что в теории Эйнштейна пространство и время взаимосвязаны и образуют единое четырёхмерное пространство. По трем осям откладывают пространственные координаты (x, y, z), а по четвертой оси откладывают временную координату ct. Любое событие характеризуется местом, где оно произошло (координаты x, y, z) и временем t, когда оно произошло. Этому событию в четырехмерном пространстве отвечает точка с координатами (x, y, z,ct). Расстояние между двумя событиями в четырехмерном пространстве называется интервалом и определяется по формуле Интервал между событиями одинаков во всех инерциальных системах отсчета, т.е. является инвариантом. Инвариантность интервала означает, что пространство и время взаимосвязаны и образуют единую форму существования материи: пространство–время. Релятивистский закон сложения скоростей 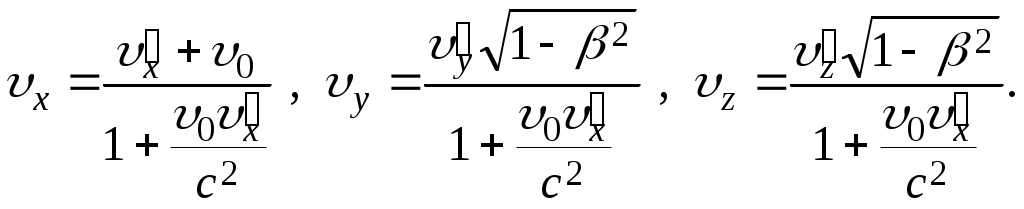 Основной закон релятивистской динамики материальной точки 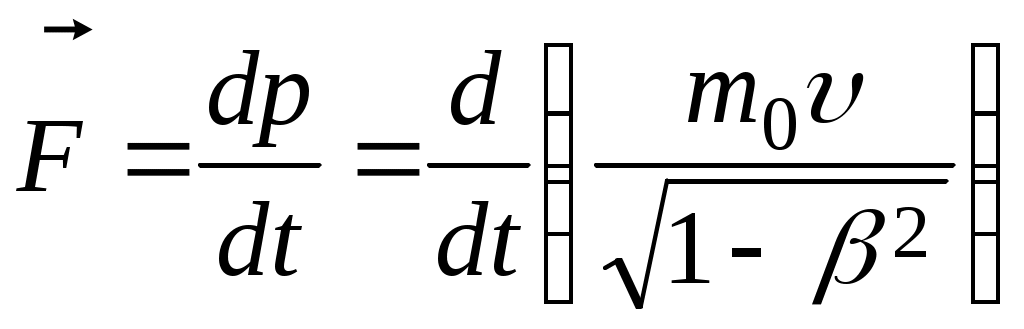 . .Полная энергия свободной частицы Энергия покоя E = m0c2 . Релятивистское выражение для кинетической энергии частицы Ek =E – E0. Контрольные задания для СРС (Лекция 4) [1,2,3,4,5,6] 1. Понятие сплошной среды. Уравнение неразрывности. 2. Уравнение Бернулли. 3. Ламинарное и турбулентное течение жидкостей. 4. Упругие напряжения. Энергия упруго деформированного тела. 5. Задачи № 4.10, 4.12, 8.26 [5] Рекомендуемая литература 1. Савельев И.В. Курс общей физики. В 5 кн. Кн.1. Механика. – М. 2001 г. 2. Савельев И.В. Курс физики. В 3 т. Т.1: Механика. Молекулярная физика – М. 1989 г. 3. Трофимова Т.И. Курс физики. – М. 2004 г. 4. Детлаф А.А., Яворский Б.М. Курс физики. – М. 1999 г. 5. Волькенштейн В.С. Сб. задач по общему курсу физики. – М. 1985 г. 6. Чертов А., Воробьев А. Задачник по физике. – М. 1988 г. Лекция 5 Статистическая физика и термодинамика — План Статистический и термодинамический методы исследования. Идеальный газ. Основное уравнение молекулярно-кинетической теории. Молекулярно-кинетический смысл температуры. Средняя кинетическая энергия молекул идеального газа. Термодинамические параметры. Равновесные состояния и процессы, их изображение на термодинамических диаграммах. Статистический метод — это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними (усреднёнными) значениями физических величин, характеризующих всю систему. Статистический метод лежит в основе молекулярной физики — раздела физики, изучающего строение и свойства вещества исходя из молекулярно-кинетических представлений. Термодинамический метод — это метод исследования систем из большого числа частиц, оперирующий величинами, характеризующими систему в целом (например, давление, объем, температура) при различных превращениях энергии, происходящих в системе, не учитывая при этом внутреннего строения изучаемых тел и характера движения отдельных частиц. Термодинамический метод лежит в основе термодинамики — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. В молекулярно-кинетической теории используют модель идеального газа. В идеальном газе: 1) пренебрегают размерами молекул; 2) молекулы не взаимодействуют между собой; 3) столкновения молекул между собой и со стенками сосуда происходят по закону абсолютно упругого удара шаров. Средняя квадратичная скорость 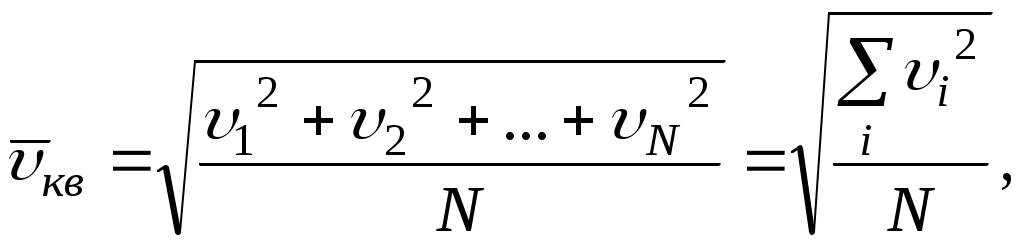 где i – скорость i–той молекулы, N – число молекул. Среднее значение кинетической энергии поступательного движения молекулы 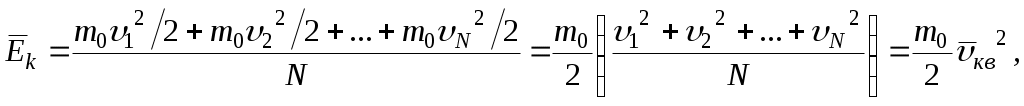 где m0 – масса одной молекулы. Основное уравнение молекулярно-кинетической теории где n – концентрация молекул. Уравнение состояния идеального газа p = nkT, где k – постоянная Больцмана. Из этих уравнений следует Термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа. Контрольные задания для СРС (Лекция 5) [1,2,3,4]Молекулярно-кинетические представления. Термодинамические параметры. Равновесные состояния и процессы, их изображение на термодинамических диаграммах. Моль, постоянная Авогадро, молярная масса, число молей. Уравнение состояния идеального газа. Газовые законы. Лекция 6 Статистические распределения — План Распределение Максвелла. Скорости теплового движения частиц. Распределение Больцмана для частиц во внешнем потенциальном поле. Число степеней свободы. Распределение энергии по степеням свободы. Внутренняя энергия идеального газа. В состоянии термодинамического равновесия в газе устанавливается некоторое стационарное равновесное состояние, когда число молекул в заданном интервале скоростей сохраняется постоянным. Функция распределения молекул по скоростям где dN – число молекул, скорости которых заключены в интервале d (от до +d), N – общее число молекул. Закон Максвелла для распределения молекул идеального газа по скоростям 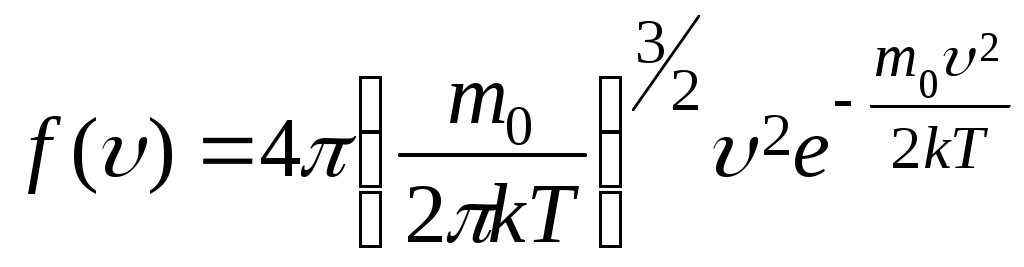 . .Конкретный вид функции распределения зависит от рода газа и температуры. Состояние газа характеризуют три скорости: наиболее вероятная, средняя квадратичная и средняя арифметическая скорость. Распределение Больцмана для частиц во внешнем потенциальном поле где n– концентрация частиц в точках поля, где потенциальная энергия частицы равна Ep, n0– концентрация частиц в точках поля, гдеEp=0. Число степеней свободы тела – это число независимых координат, которые однозначно определяют положение тела в пространстве. Материальная точка имеет три поступательные степени свободы. Абсолютно твердое тело имеет шесть степеней свободы. Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы приходится в среднем одинаковая кинетическая энергия равная Внутренняя энергия идеального газа представляет собой кинетическую энергию всех его молекул Внутренняя энергия является функцией состояния системы. Приращение внутренней энергии не зависит от вида процесса, по которому совершался переход системы из одного состояния в другое, а зависит только от начального и конечного состояний. Контрольные задания для СРС (Лекция 6) [1,2,3,4]Молекулярно-кинетические представления. Термодинамические параметры. Равновесные состояния и процессы, их изображение на термодинамических диаграммах. Моль, постоянная Авогадро, молярная масса, число молей. Уравнение состояния идеального газа. Газовые законы. Лекция 7 Основы термодинамики — План Первое начало термодинамики. Молекулярно-кинетическая теория теплоемкости идеальных газов и ее ограниченность. Энтропия. Связь энтропии с вероятностью состояния. Цикл Карно и его КПД. Второе начало термодинамики и его физический смысл. Первое начало термодинамики: количество теплоты, сообщенное системе, идет на приращение внутренней энергии системы и на работу, совершаемую системой над внешними телами. Q = U + A. Молярная теплоемкость – это количество теплоты, которое нужно для нагревания 1 моля вещества на 1°К 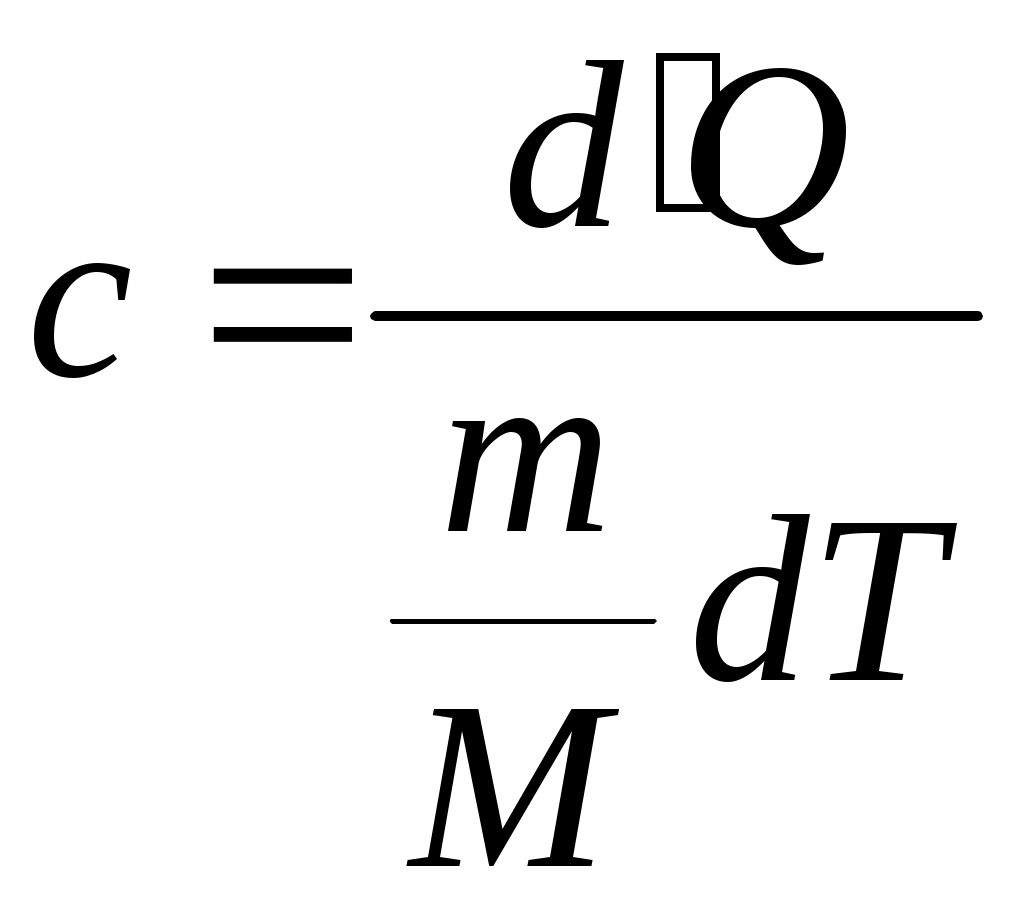 . .Теплоемкость зависит от вида процесса, при котором происходит теплопередача. Если нагревание газа происходит при постоянном объеме, то Из этой формулы следует, что теплоемкость определяется только числом степеней свободы и не зависит от температуры. Однако экспериментальные температурные зависимости теплоемкости показывают, что теплоемкость растет с ростом температуры. При низких температурах с уменьшением температуры теплоемкость уменьшается до нуля. Полное согласие с экспериментом было получено в квантовой теории теплоемкости, согласно которой энергия вращательного и колебательного движения молекул квантуется. Энтропия – функция состояния системы, элементарное изменение которой при равновесном переходе системы из одного состояния в другое, равно Статистический вес (термодинамическая вероятность) W– число микросостояний, которыми осуществляется данное макросостояние. Согласно формуле Больцмана энтропия пропорциональна логарифму статистического веса Энтропия является мерой степени беспорядка системы. Тепловая машина – периодически действующий двигатель, совершающий работу за счет получаемого извне количества теплоты. Тепловая машина состоит из нагревателя, рабочего тела и холодильника. Цикл Карно состоит из двух изотерм и двух адиабат, в качестве рабочего тела используется идеальный газ. Изменение энтропии за цикл равно нулю. К.п.д. цикла Карно К.п.д. идеальной тепловой машины, работающей по циклу Карно, не зависит от природы рабочего тела и определяется только температурами нагревателя Т1 и холодильника Т2. Второе начало термодинамики указывает направление протекания процессов в природе. Формулировка Клаузиуса: теплота не может самопроизвольно переходить от холодного тела к горячему. Формулировка Больцмана: энтропия замкнутой системы не может убывать S 0. В необратимых процессах, происходящих в замкнутой системе, энтропия возрастает, в обратимых – остается постоянной. Контрольные задания для СРС (Лекция 2) [1,2,3,4] Работа, совершаемая газом при различных процессах. Физический смысл газовой постоянной. Первое начало термодинамики для изопроцессов. Обратимые и необратимые тепловые процессы. Круговой процесс. Термодинамические потенциалы. Лекция 8 Явления переноса. Реальные газы — План Среднее число столкновений и средняя длина свободного пробега. Явления переноса в неравновесных термодинамических сисЛекциях. Коэффициенты переноса. Силы межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса. Фазовые переходы первого и второго рода. Фазовая диаграмма. Расстояние d, на которое сближаются при столкновении центры молекул, называется эффективным диаметром молекулы. Средняя длина свободного пробега молекулы – средний путь, проходимый молекулой между двумя последовательными соударениями. Среднее число столкновений в единицу времени где Средняя длина свободного пробега молекулы К явлениям переноса относятся диффузия, теплопроводность и внутреннее трение (вязкость). Неоднородности концентрации, температуры, скорости направленного перемещения отдельных слоев газа выравниваются тепловым движением. При этом отдельными молекулами переносятся: при диффузии –масса, при теплопроводности – энергия, при внутреннем трении – импульс. Диффузия – процесс выравнивания концентраций в смеси веществ, обусловленный тепловым движением. Поток массы j – это масса вещества, переносимая за единицу времени через единичную площадку, расположенную перпендикулярно направлению переноса вещества. Закон Фика: поток массы пропорционален градиенту плотности. гдеD – коэффициент диффузии. Теплопроводность – процесс выравнивания температур различных областей газа, обусловленный тепловым движением молекул. Закон Фурье: поток тепла пропорционален градиенту температуры. где – коэффициент теплопроводности. Внутреннее трение (вязкость) – это процесс выравнивания скоростей различных слоев газа (жидкости), обусловленный хаотическим движением молекул. Сила вязкости пропорциональна градиенту скорости и направлена по касательной к слоям газа: где – коэффициент вязкости. Для реальных газов нужно учитывать размеры молекул и их взаимодействие друг с другом. Между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. Уравнение состояния реального газа (уравнение Ван-дер-Ваальса) для 1 моля 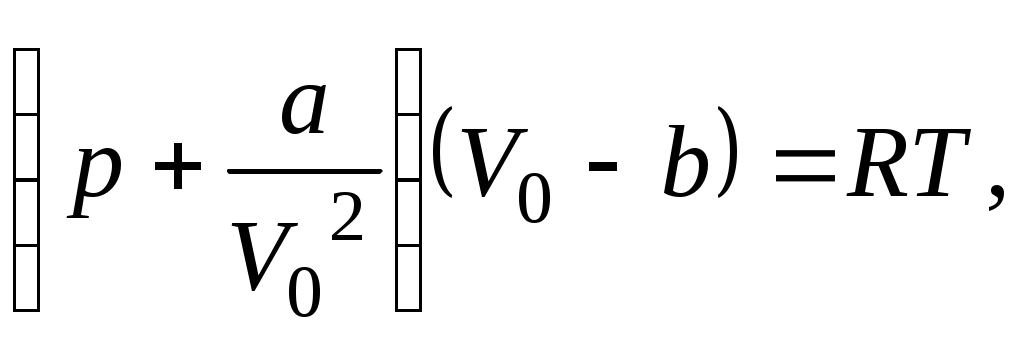 где поправки а и b– постоянные для каждого газа величины, определяемые экспериментально. Изотерма Ван-дер-Ваальса 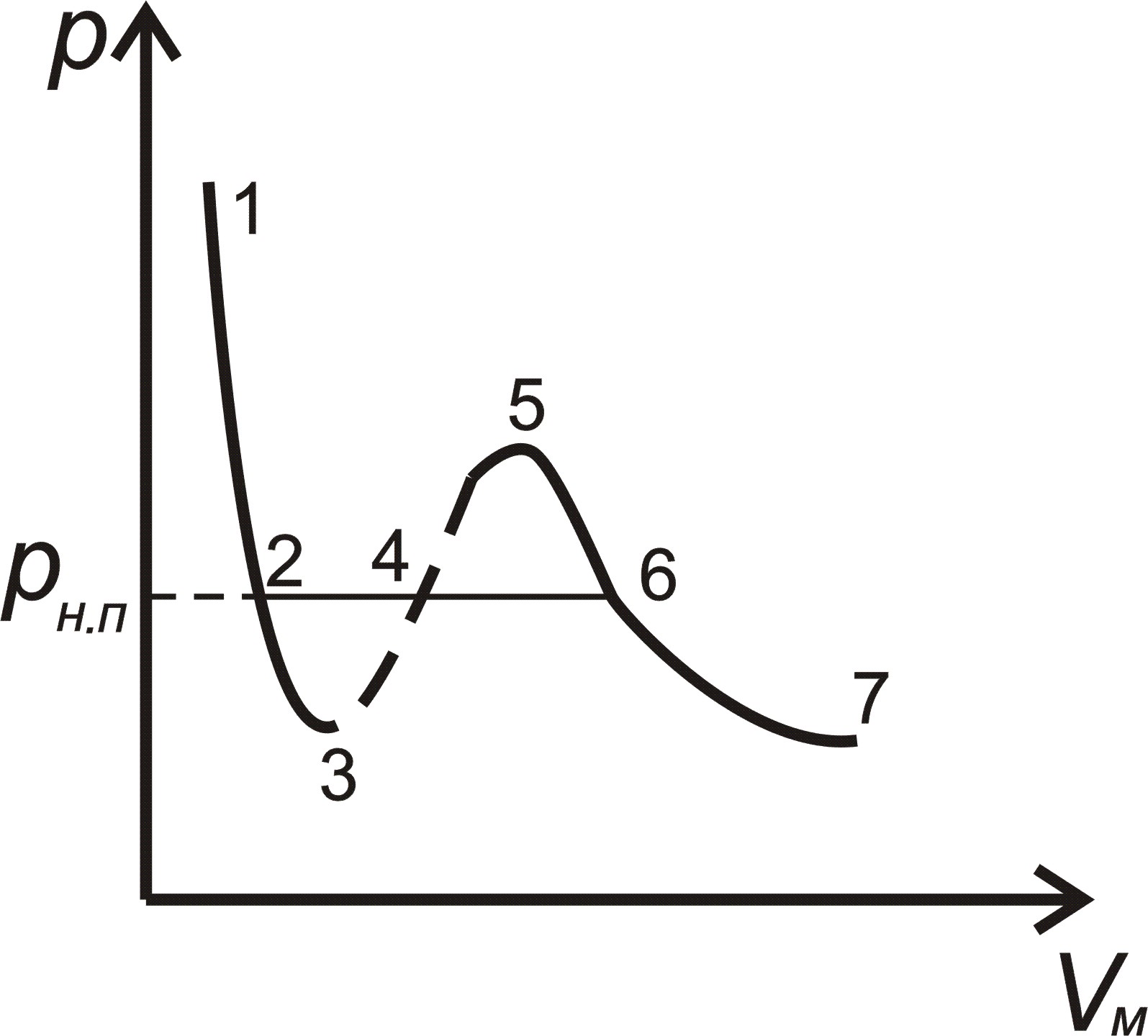 При фазовых переходах первого рода (испарение, конденсация, плавление и т.д.) поглощается или выделяется некоторое количество теплоты. При этом Т = const, энтропия, объем, характер упаковки частиц изменяются. При фазовых переходах второго рода (сверхтекучесть гелия, сверхпроводимость) происходит скачок теплоемкости. Контрольные задания для СРС (Лекция 3) [1,2,3,4] Время релаксации. Фазовые равновесия и фазовые превращения. Уравнение Клапейрона-Клаузиуса. Рекомендуемая литература 1. Савельев И.В. Курс общей физики. В 5 кн. Кн.3. Молекулярная физика и термодинамика. – М. 2001 г. 2. Савельев И.В. Курс физики. В 3 т. Т.1: Механика. Молекулярная физика – М. 1989 г. 3. Трофимова Т.И. Курс физики. – М. 2004 г. 4. Детлаф А.А., Яворский Б.М. Курс физики. – М. 1999 г. Лекция 9 Электростатика — План Заряд и его свойства. Закон Кулона. Напряженность электрического поля. Поток вектора напряженности. Теорема Гаусса. Теорема о циркуляции вектора напряженности. Потенциал и его связь с напряженностью поля. Электростатика – раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов и свойства постоянного электрического поля. Заряд – количественная мера способности тел к электрическим воздействиям. Заряд является дискретным, существует минимальное значение – элементарный заряд е = 1,610-19 Кл; подчиняется закону сохранения. Закон Кулона: два неподвижных точечных заряда отталкиваются или притягивают друг друга с силой, пропорциональной произведению модулей зарядов q1 и q2 и обратно пропорциональной квадрату расстояния r между ними. Для вакуума: Действие одних неподвижных зарядов на другие осуществляется посредством электрического поля. Силовой характеристикой электрического поля является напряженность. Напряженность электрического поля равна силе, действующей на единичный положительный пробный заряд, помещенный в данную точку поля: Сила, действующая на заряд в электрическом поле напряженностью Е: Принцип суперпозиции электрических полей: напряженность поля, создаваемого системой зарядов, равна векторной сумме напряженностей полей, создаваемых каждым из зарядов в отдельности: Поток вектора напряженности через элементарную площадку dS: а поток через площадь S: Теорема Гаусса: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри нее, деленной на 0 : 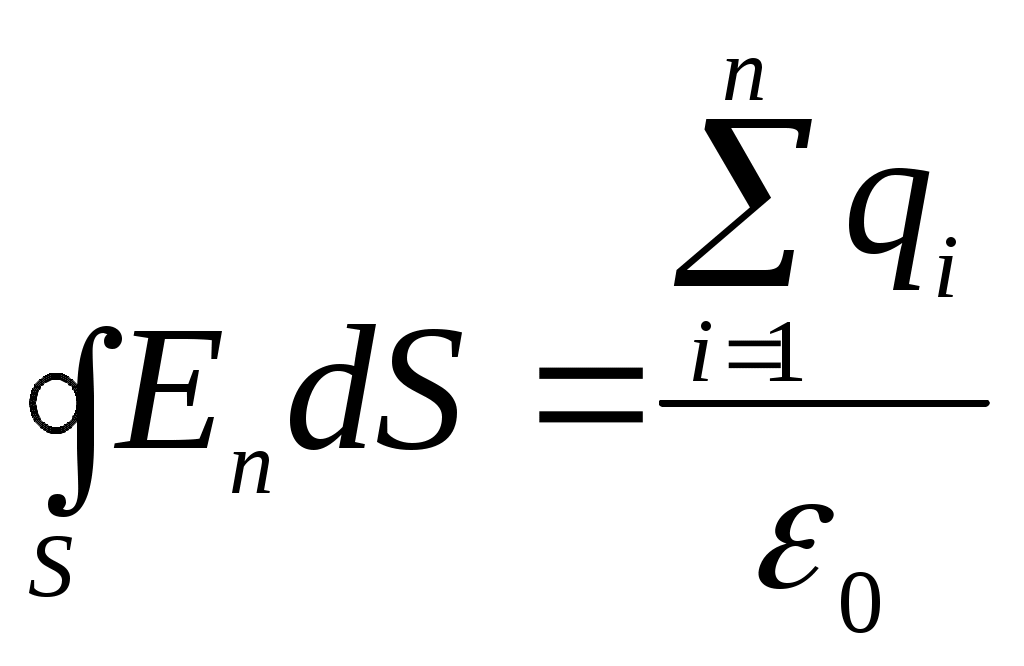 . .Если заряды распределены в пространстве с объемной плотностью : Теорема о циркуляции вектора напряженности электростатического поля: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает таким свойством, называется потенциальным. В таком поле работа консервативных сил равна убыли потенциальной энергии. Потенциал электрического поля - величина, равная работе поля по перемещению единичного положительного пробного заряда из данной точки поля в бесконечность (или, что то же самое, потенциальной энергии единичного положительного заряда, помещенного в данную точку поля): Для потенциала также справедлив принцип суперпозиции. Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля в другую, имеющие потенциалы соответственно 1и2: Связь между напряженностью и потенциалом выражается формулой: Напряженность направлена в сторону убывания потенциала. Графически распределение потенциала изображается с помощью эквипотенциальных поверхностей, перпендикулярных силовым линиям. Контрольные задания для СРС (Лекция 1) [1,2,3,4] Нарисуйте силовые линии поля точечного заряда; системы двух одноименных и разноименных точечных зарядов; равномерно заряженной бесконечной плоскости; равномерно заряженной бесконечной нити. Используя теорему Гаусса, получите формулы для напряженности поля бесконечной равномерно заряженной плоскости, бесконечной равномерно заряженной нити. 3.Чему равна напряженность поля двух плоскостей? Нарисуйте эквипотенциальные поверхности поля точечного заряда; системы двух одноименных и разноименных точечных зарядов; равномерно заряженной бесконечной плоскости; равномерно заряженной бесконечной нити. Докажите, что в любой точке поля силовые линии и эквипотенциальные поверхности взаимно ортогональны. Лекция 10 Проводники в электростатическом поле — План Электрическое поле в проводнике и вблизи от поверхности проводника. Граничные условия на границе «проводник-вакуум». Электроемкость. Конденсаторы. Емкость конденсаторов Энергия электрического поля. Во внешнем электрическом поле на концы диполя действует пара сил, которая стремится повернуть диполь таким образом, чтобы электрический момент развернулся вдоль направления поля. Во внешнем однородном поле на диполь действует вращающий момент Диэлектрики – вещества, которые при обычных условиях практически не проводят электрический ток. Диэлектрики состоят из атомов и молекул, которые можно рассматривать как электрические диполи. Существует 3 основных вида диэлектриков: неполярные: симметричные молекулы в отсутствие внешнего электрического поля имеют нулевой дипольный момент; полярные: молекулы вследствие асимметрии имеют ненулевой дипольный момент в отсутствие внешнего поля; ионные: пространственная решетка с правильным чередованием ионов разных знаков. Поляризация – изменение состояния вещества, при котором любой элемент его объема во внешнем электрическом поле приобретает дипольный момент. Мерой поляризации диэлектрика является вектор поляризации или поляризованность, которая определяется как дипольный момент единицы объема диэлектрика: При поляризации происходит ориентация диполей или появление под действием электрического поля ориентированных по полю диполей. Соответственно 3 видам диэлектриков различают 3 вида поляризации: Электронная; Дипольная; Ионная. Кристаллы, в которых возникает самопроизвольная ориентация дипольных моментов составляющих его частиц, называются сегнетоэлектриками. В случае изотропного диэлектрика поляризованность линейно зависит от напряженности электрического поля: Если поместить однородный диэлектрик во внешнее электрическое поле E0, вследствие поляризации на поверхности диэлектрика появляются связанные заряды с поверхностной плотностью ’, а поле Е’, созданное связанными зарядами, направлено против внешнего поля. Напряженность электрического поля Е зависит от свойств среды и на границе раздела 2-х диэлектриков изменяется скачкообразно. Для описания непрерывного электрического поля вводится вектор электрического смещения (электрической индукции): Теорема Гаусса для электрического поля в диэлектрике: или в случае равномерно распределенного заряда: Если в электрическое поле поместить проводник, то свободные электрические заряды начнут перемещаться до тех пор, пока поле внутри него не исчезнет, а поверхность проводника будет эквипотенциальной поверхностью. Электроемкость конденсатора: Энергия электрического поля: Объемная плотность энергии электрического поля: Контрольные задания для СРС (Лекция 11) [1,2,3,4] Чем различаются действия однородного и неоднородного электрического поля на электрический диполь? В чем заключается явление поляризации среды и как это сказывается на характеристиках электростатического поля в веществе? Чем различаются механизмы поляризации диэлектриков с полярными и неполярными молекулами? Какова разница между свободными и связанными зарядами? В чем отличие явления электростатической индукции в проводнике и диэлектрике? Условия для векторов напряженности и электрической индукции на границе раздела двух диэлектриков. Электроемкость цилиндрического и сферического конденсаторов. Последовательное и параллельное соединения конденсаторов. Лекция 11 Диэлектрики в электрическом поле — План Диполь. Виды диэлектриков. Поляризация диэлектриков. Поляризованность. Диэлектрическая проницаемость среды. Электрическое смещение. Энергия электрического поля. Диполь – система двух равных по модулю разноименных точечных зарядов, расстояние между которыми гораздо меньше расстояний до рассматриваемых точек. Электрический момент диполя Во внешнем электрическом поле на концы диполя действует пара сил, которая стремится повернуть диполь таким образом, чтобы электрический момент развернулся вдоль направления поля. Во внешнем однородном поле на диполь действует вращающий момент Диэлектрики – вещества, которые при обычных условиях практически не проводят электрический ток. Диэлектрики состоят из атомов и молекул, которые можно рассматривать как электрические диполи. Существует 3 основных вида диэлектриков: неполярные: симметричные молекулы в отсутствие внешнего электрического поля имеют нулевой дипольный момент; полярные: молекулы вследствие асимметрии имеют ненулевой дипольный момент в отсутствие внешнего поля; ионные: пространственная решетка с правильным чередованием ионов разных знаков. Поляризация – изменение состояния вещества, при котором любой элемент его объема во внешнем электрическом поле приобретает дипольный момент. Мерой поляризации диэлектрика является вектор поляризации или поляризованность, которая определяется как дипольный момент единицы объема диэлектрика: При поляризации происходит ориентация диполей или появление под действием электрического поля ориентированных по полю диполей. Соответственно 3 видам диэлектриков различают 3 вида поляризации: Электронная; Дипольная; Ионная. Кристаллы, в которых возникает самопроизвольная ориентация дипольных моментов составляющих его частиц, называются сегнетоэлектриками. В случае изотропного диэлектрика поляризованность линейно зависит от напряженности электрического поля: Если поместить однородный диэлектрик во внешнее электрическое поле E0, вследствие поляризации на поверхности диэлектрика появляются связанные заряды с поверхностной плотностью ’, а поле Е’, созданное связанными зарядами, направлено против внешнего поля. Напряженность электрического поля Е зависит от свойств среды и на границе раздела 2-х диэлектриков изменяется скачкообразно. Для описания непрерывного электрического поля вводится вектор электрического смещения (электрической индукции): Теорема Гаусса для электрического поля в диэлектрике: или в случае равномерно распределенного заряда: Контрольные задания для СРС (Лекция 11) [1,2,3,4] Чем различаются действия однородного и неоднородного электрического поля на электрический диполь? В чем заключается явление поляризации среды и как это сказывается на характеристиках электростатического поля в веществе? Чем различаются механизмы поляризации диэлектриков с полярными и неполярными молекулами? Какова разница между свободными и связанными зарядами? В чем отличие явления электростатической индукции в проводнике и диэлектрике? Условия для векторов напряженности и электрической индукции на границе раздела двух диэлектриков. Электроемкость цилиндрического и сферического конденсаторов. Последовательное и параллельное соединения конденсаторов. Лекция 12 |
