кер. Лекция №1. Лекция 1 Множества Определение множества, способы задания, операции над множествами
 Скачать 116.14 Kb. Скачать 116.14 Kb.
|
|
Лекция №1: Множества Определение множества, способы задания, операции над множествамиТеория множеств опирается на три первичных понятия: множество; элемент; принадлежность. Строгого определения этим понятиям не дается, описывается только их применение. На рисунке 1.1 буквой  обозначено множество, элементами которого являются точки заштрихованной части плоскости, при этом точка обозначено множество, элементами которого являются точки заштрихованной части плоскости, при этом точка 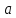 принадлежит множеству принадлежит множеству  , точка , точка 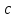 не принадлежит множеству не принадлежит множеству  . . Рис. 1.1. Способы задания множества Множество можно задать, перечислив все его элементы: 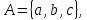  . Порядок записи элементов множества произволен. Часто задают множество, указав его характеристическое свойство, которое для каждого элемента позволяет выяснить, принадлежит он множеству или нет. . Порядок записи элементов множества произволен. Часто задают множество, указав его характеристическое свойство, которое для каждого элемента позволяет выяснить, принадлежит он множеству или нет.Например,  , , . .В дальнейшем для известных числовых множеств будут использоваться обозначения:  – множество натуральных чисел; – множество натуральных чисел;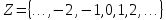 – множество целых чисел; – множество целых чисел;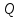 – множество рациональных чисел; – множество рациональных чисел; – множество действительных чисел. – множество действительных чисел.Основные определения Пустым множеством называется множество  , не содержащие ни одного элемента, т.е. для любого элемента x выполняется , не содержащие ни одного элемента, т.е. для любого элемента x выполняется  . .Универсальным множеством называется множество  всех элементов, рассматриваемых в данной задаче. всех элементов, рассматриваемых в данной задаче.Пример 1.1. Пусть  и требуется найти все решения уравнения и требуется найти все решения уравнения  . Множеством . Множеством  решений этой задачи есть пустое множество: решений этой задачи есть пустое множество:  . .Пусть теперь  . Тогда множество . Тогда множество  решений уравнения решений уравнения  не пусто: не пусто: 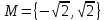 . .Будем говорить, что множество  включается во множество включается во множество  , если каждый элемент множества , если каждый элемент множества  является элементом множества является элементом множества  (говорят также, что (говорят также, что  является подмножеством множества является подмножеством множества  ). Из определения включения следуют свойства: ). Из определения включения следуют свойства: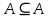 для любого множества для любого множества  ; ;Если  и и  , то , то  ; ;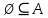 для любого множества для любого множества  ; ; для любого множества для любого множества  . .Определим понятие равенства множеств:  тогда и только тогда, когда одновременно выполняются два включения тогда и только тогда, когда одновременно выполняются два включения  и и 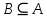 , т.е. каждый элемент множества , т.е. каждый элемент множества  является элементом множества является элементом множества  и каждый элемент множества и каждый элемент множества  является элементом множества является элементом множества  . .Диаграммы Эйлера – Венна Эти диаграммы применяются для наглядного изображения множеств и их взаимного расположения. Универсальное множество  изображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.2). изображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.2). Рис. 1.2. Диаграмма Эйлера-Венна Операции над множествами Объединением множеств  и и  называется множество называется множество  , состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств , состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств  или или  (рис. 1.3, а). (рис. 1.3, а).Пример 1.2. Если  , ,  , то , то  . .Пересечением множеств  и и  называется называется  , состоящее из тех и только тех элементов, которые принадлежат одновременно и множеству , состоящее из тех и только тех элементов, которые принадлежат одновременно и множеству  , и множеству , и множеству  (рис. 1.3, б). (рис. 1.3, б).Пример 1.3. Если  , ,  , то , то  . . Рис. 1.3. Операции над множествами: объединение множеств  и и  ; ;пересечение множеств  и и  . .Разностью множеств  и и  называется множество называется множество  тех и только тех элементов, которые принадлежат множеству тех и только тех элементов, которые принадлежат множеству  и не принадлежат множеству и не принадлежат множеству  (рис. 1.4, а). (рис. 1.4, а).Пример 1.4.  ; ;  . .Дополнением множества  до универсального до универсального  назыается множесто назыается множесто 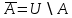 (рис. 1.4, б). (рис. 1.4, б).Пример 1.5. Если  , ,  , то , то  . .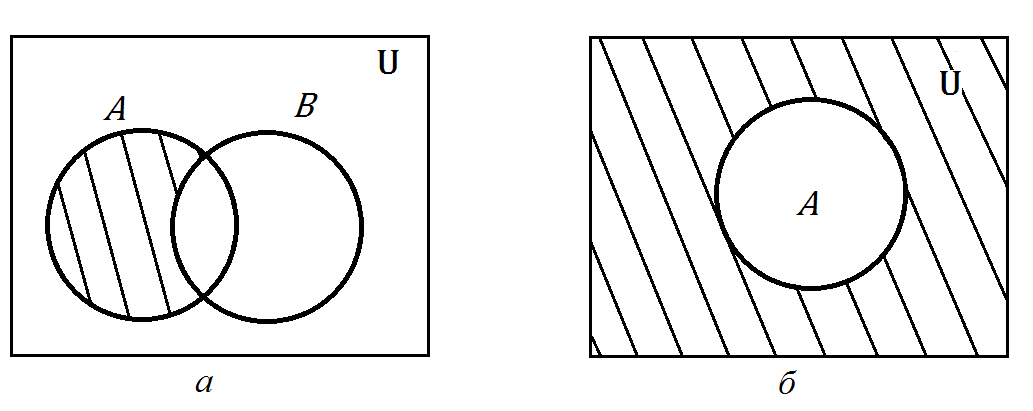 Рис. 1.4. Операции над множествами: разность множеств  и и  ; ;дополнение множества  . .Системы множеств Элементы множества сами могут быть множествами: 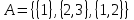 ; в таком случае удобно говорить о системе множеств. Рассмотрим такие системы множеств, как булеан и разбиение множеств. ; в таком случае удобно говорить о системе множеств. Рассмотрим такие системы множеств, как булеан и разбиение множеств.Булеаном  множества множества  называется множество всех подмножеств множества называется множество всех подмножеств множества  . Например, для множества . Например, для множества  булеаном является множество булеаном является множество  . .Разбиением  множества множества  называется система его непустых непересекающихся подмножеств, в объединении дающая множество называется система его непустых непересекающихся подмножеств, в объединении дающая множество  (рис. 1.5). (рис. 1.5).Например, для множества  можно построить разбиение можно построить разбиение  , состоящие из двух элементов (они называются блоками разбиения), или разбиение , состоящие из двух элементов (они называются блоками разбиения), или разбиение  – из четырех блоков, возможны и другие разбиения этого множества – из четырех блоков, возможны и другие разбиения этого множества  . .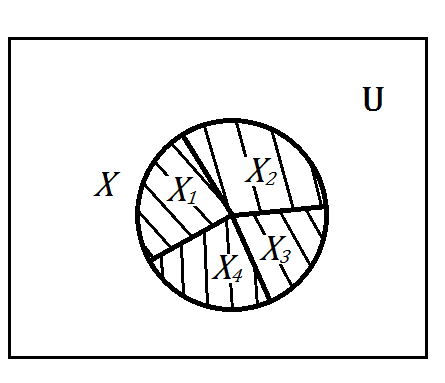 Рис. 1.5. Разбиение множества 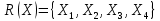 Законы алгебры множеств Так же, как операции обычной алгебры, операции над множествами выполняются по законам (табл. 1.1), которые доказываются на основе введенных выше определений. Особенностью алгебры множеств является закон идемпотентности, благодаря которому в алгебре множеств нет числовых коэффициентов и степеней. Таблица 1.1: Законы алгебры множеств
Бинарное отношениеДекартовым произведением  двух множеств двух множеств  и и  называется множество всех упорядоченных пар называется множество всех упорядоченных пар  таких, что таких, что  , а , а  . .Пример 1.6. Пусть  , ,  . Тогда . Тогда , , Очевидно, что  , т.е. для операции декартова произведения множеств закон коммутативности не выполняется. , т.е. для операции декартова произведения множеств закон коммутативности не выполняется.Наглядно декартово произведение множеств можно представить в виде графика. На рис. 1.6 звездочками отмечены элементы множества  . .Декартовым произведением множеств  будем называть множество будем называть множество  всех упорядоченных наборов всех упорядоченных наборов  таких, что таких, что  . . Рис. 1.6. График декартова произведения  Определение бинарного отношения Пусть среди трех людей (назовем их Андрей, Василий и Сергей) двое знакомы друг с другом (Андрей и Василий) и знают третьего (Сергея), но тот их не знает. Как описать отношение между этими людьми? Имеем множество  , из элементов которого составлены упорядоченные пары: , из элементов которого составлены упорядоченные пары:  , , 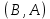 , ,  , ,  , т.е. выделено некоторое подмножество декартова произведения , т.е. выделено некоторое подмножество декартова произведения 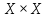 . Это подмножество и описывает связи между элементами множества . Это подмножество и описывает связи между элементами множества  . .Определение. Говорят, что на множестве  задано бинарное отношение задано бинарное отношение  , если задано подмножество декартова произведения , если задано подмножество декартова произведения 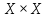 (т.е. (т.е. 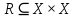 ). ).Пример 1.7. Пусть  . Зададим на . Зададим на  следующие отношения: следующие отношения: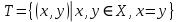 – отношение равенства; – отношение равенства;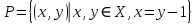 – отношение предшествования; – отношение предшествования; – отношение делимости. – отношение делимости.Все эти отношения заданы с помощью характеристического свойства. Ниже перечислены элементы этих отношений:  ; ; ; ; . .Тот факт, что пара  принадлежит данному отношению принадлежит данному отношению  , будем записывать: , будем записывать: 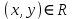 или или 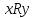 . Например, для отношения . Например, для отношения 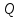 запись запись  означает, что 4 на 2 нацело, т.е. означает, что 4 на 2 нацело, т.е. 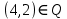 . .Областью определения  бинарного отношения бинарного отношения  называется множество называется множество 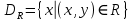 . .Областью значений  называется множество называется множество  . .Так, для отношения  из примера 1.7 областью определения является множество из примера 1.7 областью определения является множество 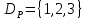 , а областью значений – , а областью значений –  . .Способы задания бинарного отношения Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Существуют и более наглядные способы задания бинарного отношения: график отношения, схема отношения, граф отношения, матрица отношения. График отношения изображается в декартовой системе координат; на горизонтальной оси отмечается область определения, на вертикальной – область значений отношения; элементу отношения  соответствует точка плоскости с этими координатами. На рис. 1.7, а приведен график отношения соответствует точка плоскости с этими координатами. На рис. 1.7, а приведен график отношения 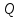 примера 1.7. примера 1.7.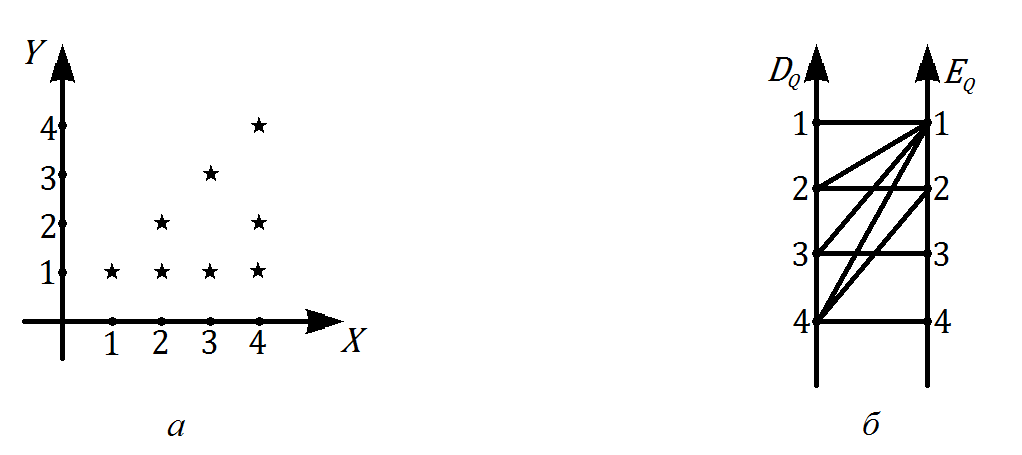 Рис. 1.7. График отношения 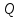 (а) и схема отношения (а) и схема отношения 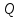 (б) (б)Схема отношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент  принадлежит отношению принадлежит отношению  , то соответствующие точки из , то соответствующие точки из  и и  соединяются прямой. На рис. 1.7, б приведена схема отношения соединяются прямой. На рис. 1.7, б приведена схема отношения 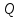 из примера 1.7. из примера 1.7.Граф отношения 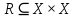 строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множества строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множества  . Пара точек . Пара точек  и и 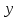 соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара  принадлежит отношению принадлежит отношению  . На рис. 1.8, а приведен граф отношения . На рис. 1.8, а приведен граф отношения 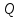 примера 1.7. примера 1.7.Матрица отношения 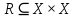 – это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества – это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества  . На пересечении строки . На пересечении строки  и столбца и столбца 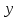 ставится 1, если пара ставится 1, если пара 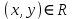 ; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй – номеру столбца. Пусть ; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй – номеру столбца. Пусть  . Тогда матрица отношения . Тогда матрица отношения 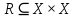 имеет имеет 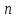 строк и строк и 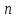 столбцов, а ее элемент столбцов, а ее элемент  определяется по правилу: определяется по правилу: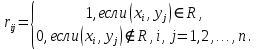 На рис. 1.8, б приведена матрица отношения 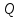 примера 1.7. примера 1.7. Рис. 1.8. Граф отношения 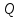 (а) и матрица отношения (а) и матрица отношения 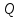 (б) (б)Свойства бинарных отношений Бинарные отношения делятся на типы в зависимости от свойств, которыми они обладают. Рассмотрим следующие отношения на множестве  : : ; ; ; ; ; ;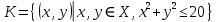 . .Отношение  на множестве на множестве  называется рефлексивным, если для всех называется рефлексивным, если для всех  выполняется условие выполняется условие  . Среди приведенных выше отношений рефлексивными являются отношение . Среди приведенных выше отношений рефлексивными являются отношение  (т.к. неравенство (т.к. неравенство  справедливо при всех справедливо при всех  ) и отношение ) и отношение  (т.к. разность (т.к. разность  делится на 3, значит, пара делится на 3, значит, пара 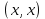 принадлежит отношению принадлежит отношению  при всех при всех  ). ).Отношение  на множестве на множестве  называется антирефлексивным, если условие называется антирефлексивным, если условие  не выполняется ни при одном не выполняется ни при одном  . Примером антирефлексивного отношения является отношение . Примером антирефлексивного отношения является отношение  (неравенство (неравенство  не выполняется ни при каких значениях не выполняется ни при каких значениях  , следовательно, ни одна пара , следовательно, ни одна пара 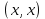 не принадлежит отношению не принадлежит отношению  ). Отметим, что отношение ). Отметим, что отношение  не является рефлексивным не является рефлексивным  и не является антирефлексивным и не является антирефлексивным 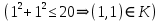 . .Отношение  на множестве на множестве  называется симметричным, если из условия называется симметричным, если из условия 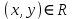 следует следует  . Симметричными являются отношения . Симметричными являются отношения  (если (если  делится на 3, то и делится на 3, то и  делится на 3) и делится на 3) и  (если (если  , то и , то и  ). ).Отношение  на множестве на множестве  называется несимметричным, если для любых называется несимметричным, если для любых  из условия из условия 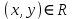 следует следует  . Несимметричным является отношение . Несимметричным является отношение  , т.к. условия , т.к. условия  и и  не могут выполняться одновременно (только одна из пар не могут выполняться одновременно (только одна из пар  или или  принадлежит отношению принадлежит отношению  ). ).Отношение  на множестве на множестве  называется антисимметричным, если для любых называется антисимметричным, если для любых  из условия из условия 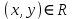 и и  следует следует  . Антисимметричным является отношение . Антисимметричным является отношение  , т.к. из одновременного выполнения , т.к. из одновременного выполнения  и и  следует следует  . .Отношение  на множестве на множестве  называется транзитивным, если для любых называется транзитивным, если для любых 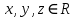 из одновременного выполнения условий из одновременного выполнения условий 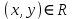 и и  следует следует  . Отношения . Отношения  , ,  , ,  являются транзитивными, а отношение являются транзитивными, а отношение  нетранзитивно: если нетранзитивно: если  , то , то  и и  , но , но  , то есть выполняются условия , то есть выполняются условия  и и  , но , но  . .Отношения эквивалентности Рассмотрим три отношения:  , ,  , ,  . Отношение . Отношение  . Отношение . Отношение  введем на множестве введем на множестве  всех треугольников следующим образом: этому отношению принадлежат пары треугольников такие, что площадь треугольника всех треугольников следующим образом: этому отношению принадлежат пары треугольников такие, что площадь треугольника  равна площади треугольника равна площади треугольника 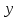 . .Отношение  действует на множестве жителей г. Томска и содержит пары действует на множестве жителей г. Томска и содержит пары  такие, что такие, что  и и 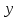 носят шляпы одинакового размера. носят шляпы одинакового размера.Свойства этих трех отношений приведены в таблице 1.2, где Р означает рефлексивность, АР – антирефлексивность, С – симметричность, АС – антисимметричность, НС – несимметричность, Т – транзитивность отношения. В качестве упражнения проверьте правильность заполнения таблицы, пользуясь определениями свойств бинарных операций. Таблица 1.2: Свойства отношений
Мы видим, что отношения обладают одинаковыми свойствами, поэтому их относят к одному типу. Определение. Отношение  на множестве на множестве  называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности, транзитивности. называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности, транзитивности.Таким образом, отношения  , ,  , ,  являются отношениями эквивалентности на соответствующих множествах являются отношениями эквивалентности на соответствующих множествах  . Важной особенностью отношений эквивалентности является то, что они разбивают все множество . Важной особенностью отношений эквивалентности является то, что они разбивают все множество  на непересекающиеся подмножества – классы эквивалентности. на непересекающиеся подмножества – классы эквивалентности.Определение. Классом эквивалентности, порожденным элементом  , называется подмножество , называется подмножество  множества множества  , для элементов которого выполняется условие , для элементов которого выполняется условие  . Таким образом, класс эквивалентности . Таким образом, класс эквивалентности 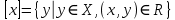 . .Так, отношение  разбивает множество разбивает множество  на три класса эквивалентности: на три класса эквивалентности: 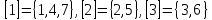 . Класс, порожденный элементом 4, совпадает с классом . Класс, порожденный элементом 4, совпадает с классом 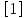 ; ;  . .Классы эквивалентности образуют систему непустых непересекающихся подмножеств множества  , в объединении дающую все множество , в объединении дающую все множество  – т.е. образует разбиение множества – т.е. образует разбиение множества  . .Отношение эквивалентности обозначают  ,поэтому определение класса эквивалентности можно записать так: ,поэтому определение класса эквивалентности можно записать так:  . .Отношение порядка Рассмотрим отношение  , ,  : :  ; ;  , отношение , отношение  и отношение включения и отношение включения 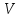 на множестве всех подмножеств целых чисел ( на множестве всех подмножеств целых чисел ( – булеан множества – булеан множества  ): ): 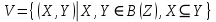 . .Таблица 1.3: Свойства отношений
Мы видим, что по свойствам эти отношения разделились на два типа. Определение. Отношение  на множестве на множестве  , обладающее свойствами рефлексивности, антисимметричности, транзитивности, называется отношением порядка на множестве , обладающее свойствами рефлексивности, антисимметричности, транзитивности, называется отношением порядка на множестве  (обозначается (обозначается  ). ).Определение. Отношение  на множестве на множестве  , обладающее свойствами антирефлексивности, несимметричности, транзитивности, называется отношением строгого порядка (обозначается , обладающее свойствами антирефлексивности, несимметричности, транзитивности, называется отношением строгого порядка (обозначается  ). ).Таким образом, отношения  , , 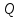 , , 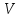 являются отношениями порядка на соответствующих множествах, а отношение являются отношениями порядка на соответствующих множествах, а отношение  – отношением строгого порядка. – отношением строгого порядка. |

 ;
; 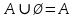 ;
; 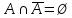
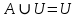 ;
;  ;
; 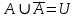
 ;
; 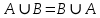
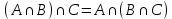 ;
;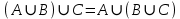
 ;
;

 ;
; 
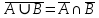 ;
; 
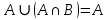 ;
; 