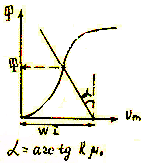Главная страница
Навигация по странице:

  • 7-ШІ БӨЛІМ . ТӨРТҰШТЫҚТАР 18 ЛЕКЦИЯ . 18.1 Төртұштықтың анықтамалары.

  • 18.3. А – формасындағы теңдеудіңшешімі.

  • П-схема сы

  • Т- схема сы П-схема

    		•

    РЕФ ЛЕК КОНС. Лекция. 1 Негізгі анытамалар


    Скачать 4.03 Mb.
    НазваниеЛекция. 1 Негізгі анытамалар
    АнкорРЕФ ЛЕК КОНС
    Дата25.01.2022
    Размер4.03 Mb.
    Формат файлаdoc
    Имя файлаlektsiya konspekti.doc
    ТипЛекция
    #341648
    страница3 из 3
    1   2   3

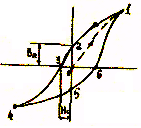
    Синусоидалы емес кернеудегі тізбек алгоритм анализі

    Тізбектің R,L,C мәндері белгілі және синусоидалы кернеу болғанда , сур.39 тізбек үшін синусоидалы емес U кернеу, I ток пен тізбектің Р активті қуаттын анықтау керек.

    Ток үшін бірінші және үшінші гармоника тізбегінің толық кедергісі анықталады.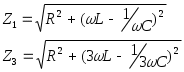



    Гармоникалық токтың амплитудалық мәндері Ом заңы бойынша табылады:



    Жұмыс істейтін токтың мәндерін амплитудалық мәндер арқылы табылады:



    Жұмыс істейтін синусоидалы емес токтың мәні анықталады:



    Жұмыс істейтін синусоидалы емес кернеудің мәні анықталады: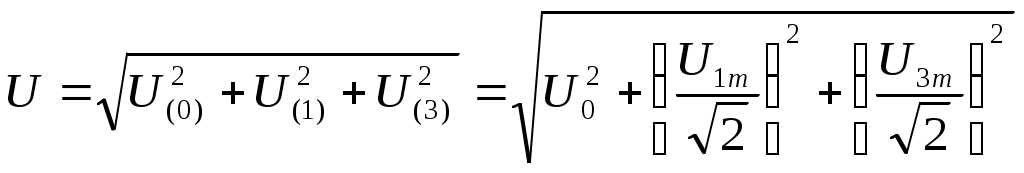



    1. Жұмыс істейтін токтың мәнін біле, активті қуатты есептеуге болады:


    6-ШЫ БӨЛІМ. МАГНИТТІ ТІЗБЕКТЕР

    16 ЛЕКЦИЯ.

    16.1. Тұрақты магниттелу күші бар магнитті тізбектер.

    Магнитті өрісті сипаттайтын негізгі шамаларе:

    1. Магниттік индукция - магниттік өрістің әр нуктесіндегі интенсивтілігін анықтайды, В әріпімен белгіленеді. Индукция өлшем бірлігі Вб/м2. Бұл бірлікті Тесла (Т) деп атайды. Магниттік индукция дегеніміз - бір қалыпты магнит өрістіндегі оның күш сызықтарына перпендикуляр орналасқан өткізгіштің 1м ұзындығынан 1А ток өткендегі күшке тең шама. Магниттік индукция векторлық шама болып табылады.Бағыты өрістің бағытымен бірдей болады.

    2. Магниттелу J – магниттік момент зат көлемінің бірлігі. ӨЖ өлшем бірлігі – А/м.

    3. Магнитті өріс кернеулігі Н - кернеу магнитті өрістің сандық мінездемесі болып табылады және ортаның магнитті қасиеттеріне байланысты емес. ӨЖ өлшем бірлігі – А/м.

    4. Магниттік ағын Ф - бірқалыпты өрістің магнитті индукция В мен индукция векторына перпендикуляр S ауданы шамасына көбейтіндісін, магнит ағыны дейміз. ӨЖ өлшем бірлігі – Ф (Вебер).

    5. μ –заттың магниттік өтімділігіне қатысты немесе магнитті өрістің ұдаю коэффициенті.

    6. μ0 – тұрақтылық, вакуумның магниттік қасиетін сипаттайтын. ӨЖ-де μ0 = 4π 10-7 Гн/м.

    Ферромагнитті орта үшін индукция жмен магниттік өрістің кернеулігі келесі байланыспен байланысты:

    В= μ μ0 Н

    Вакуумдағы индукция жмен магниттік өрістің кернеулігі келесі байланыспен байланысты:

    В0= μ0 Н

    Толық тоқ заңы: ℓ

    Ферромагнитті материалдардың сипаттамасы.




    ВR- магниттікая индукцияның қалдығы

    HR-коэрцитивті күш

    Сур. 41. Біріншілік магниттелу қисық сызығы
    Сур.42. Ферромагнитті материалдың магниттелу қисықсызығы

    Магнитті тізбектің классификациясы
    Қарапайым (тұйықталмаған) =>

    Біртекті, біртексіз

    Магнитті тізбек =>









    Күрделі (тұйықталған) =>
    Біртекті, біртексіз

    Магнитті тізбектердің заңдары.

    1. Ом заңы


    2. Кирхгофтың бірінші заңы


    3. Кирхгофтың екінші заңы



    Магнитті тізбектредің әдісіне талдау жасау

    1. Тура тапсырма : Ф → WI

    2. Кері тапсырма: WI → Ф

    Біртекті магнитті тізбектерді талдау

    Тура тапсырма
    Алгоритм

    Берілгені: Ф, өлшемі,

    Магниттелу қисығыя B=f(H)

    Анықтау керек: WI

    1. Ф → В (Ф=В S)

    2. В → H

    3. H → Hℓ

    Кері тапсырма
    Алгоритм

    Берілгені: WI, өлшемдері,

    Магниттелу қисығыя B=f(H)

    Анықтау керек: Ф

    1. Hℓ=WI → H

    2. H → B

    3. В → Ф




    Біртексыз магнитті тізбектерді талдау

    Тура тапсырма
    Алгоритм

    Берілгені: Ф, өлшемі,

    Магниттелу қисығыя B=f(H)

    Анықтау керек: WI

    1. Ф → В (Ф=В S)

    2. В → H

    3. В=В0 → H0

    4. WI=Hℓ+H0ℓ0

    Кері тапсырма
    Алгоритм

    Берілгені: WI, өлшемдері,

    Магниттелу қисығыя B=f(H), B=f(H0)

    Анықтау керек: Ф



    17 ЛЕКЦИЯ

    17.1 Айнымалы магниттелу күші бар магнитті тізбек .


    Синусоидалы кернеу көзіне қосылған магнитті сымы бар орама, айнымалы ток орамада өзіндік инкуцияланған ЭҚК қоздырады


    Сур .43.Магнитті сымы бар орама



    Егер , онда уақытпен өзгерген магнит ағынының заңы:

    мұнда =



    Сур.44. Векторлы диаграмма

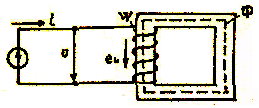
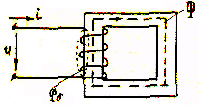
    Тұйықталған магнитті сымдағы процестер.

    Магнитты сымсыз индуктивті орама







    Сур.45. Вебер-амперлі сипаттама

    Идеалдандырылған орама





    Сур.46. Вебер-амперлі сипаттама

    Идиалдандырылған орамада индуктивтілік шашу және активті кедергі болмайды. Идиалдандырылған ораманың қасиеті тек магнитті сымның параметрінен және оның магниттелу режиміне байланысты.

    Реалды орама магнитті сымымен








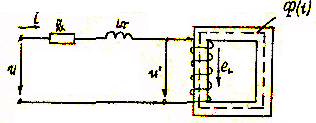
    Эквивалентті синусоидалы ток

    Синусоидалы кернеу кезіндемагнитті сымы бар орамадағы ток – синусоидалы емес. Магнитті тізбекке талдау кезінде синусоидалы емес ток эквивалентті синусоидалы токпен алмастырылады, оның әрекет ету мәні келесі түрде анықталады: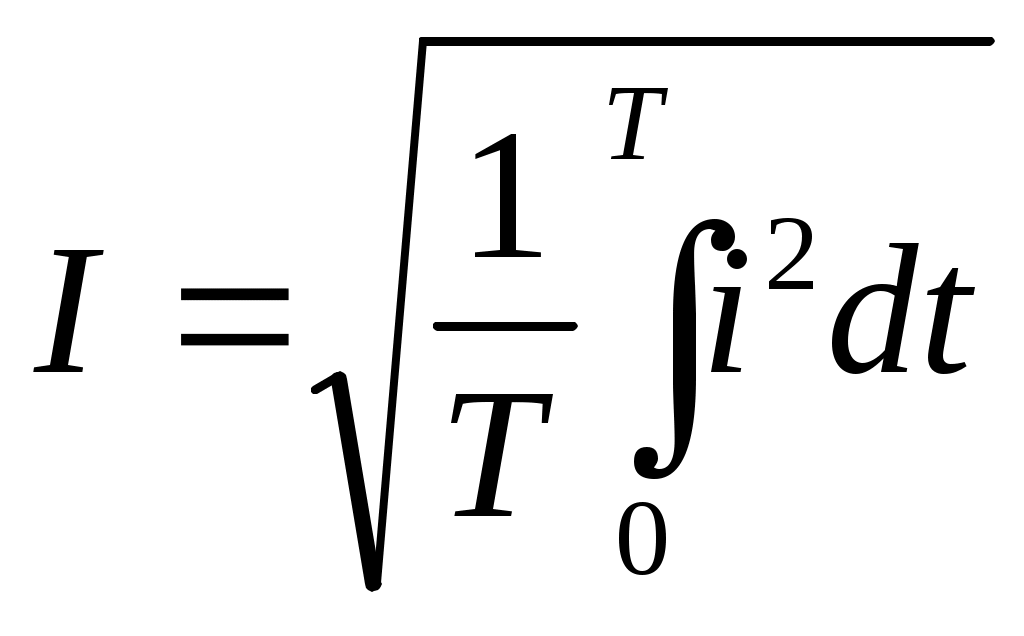



    Эквивалентті синусоидалы токты анықтау алгоритмі

    Берілгені:


    1. магнитті сымның өлшемі және материалы;

    2.U – тораптағы кернеу;

    3.f – тораптағы жиілік ;

    4.W – ораманың орам саны;

    5.магнитті шығынның үдеулік қисығы
    Анықтау керек:

    1.U → Фm →Bm

    2. Bm → (p0 , q0)- активті және реактивті магниттік шығынды;

    3. p0 → P= p0 G (G – вес)

    q0 → Q= q0 G

    4.S=

    5.S → I=S/U

    Идиалдандырылған ораманың алмасу схемасы және векторлы диаграммасы.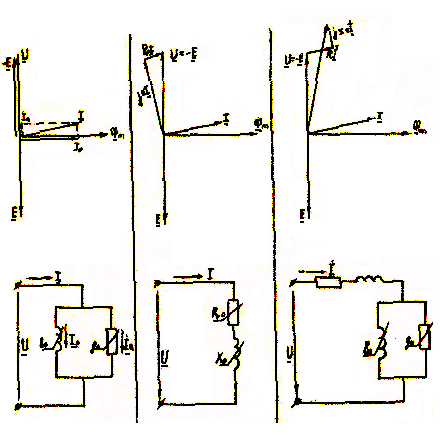

    Сур. 47

    7-ШІ БӨЛІМ . ТӨРТҰШТЫҚТАР

    18 ЛЕКЦИЯ .

    18.1 Төртұштықтың анықтамалары.

    Төртұштық – бұл электрлік тізбектің қысқыштарына қатысты қарастырылатын жалпылама түсінік.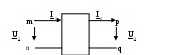



    Сур. 48. Төртұштықтың кескінделуі.

    mn және pq – қысқыштардың жұмыс жұптары; mn – қысқыштардың кіріс жұбы; pq - қысқыштардың шығыс жұбы

    18.2. Төртұштықтардың жазылу теңдеу формасы.

    Формалар
    Теңдеуі

    A – формасы
    U 1 = AU 2 + BI 2 ; I 1 = CU 2 + DI 2

    Y – формасы
    I 1 = Y 11U 1 + Y 12 U 2 ; I 2 = Y 21 U 1+ Y 22 U2

    Z – формасы
    U 1 = Z 11 I 1 + Z 12 I 2; U 2= Z 21 I 1 + Z 22 I 2

    H - формасы
    U 1 = H11 I 11 + H12 U 2 ; I 2= H21 I 1 + H22 U 2

    G - формас
    I 1 = G11U 1 + G 12 I 2 ; U 2 = G21 U 1+ G22 I 2

    B - формасы
    U 2 = B11U 1 + B12 I 1 ; I 2 = B21 U 1+ B22 I1

    18.3. А – формасындағы теңдеудіңшешімі.

    Өзара шартты қанағаттандыратын A, B, C, D, коэффициенттері үшін А – формасы келесі байланысқа қатысты.

    AD – BC = 1

    Mn қысқыштарына (сур.48) ЭҚК қорегі қосылған : E=Umn = U 1 pq – жүктемесіне қосылған Z 2 . Жүктемедегі кернеу: U 2= I 2 = Z 2 = U pq

    I 2 тоғына бағытталған Z 2 жүктемесіне ЭҚК корегін қосыамыз Е2 = U 2, I 1 және I 2 тоқтарына теңдеулер жазамыз,оны Е1 и Е2 арқылы көрсетемыз :

    I 1 = Y 11 Е1 + Y 12 Е2 (1)

    I 2 = Y 21 Е1 + Y 22 Е2 (2)

    (2 )теңдеуінен аламыз:

    Е1 = Е2 + I2 (3)

    (3)теңдеуіне (1) қойып , аламыз:

    I 1 = Е2 I 2 (4)

    Белгілейміз:

    А= В= С= D=

    (3) және (4) теңдеулерінен Е1 ді U1 ге және Е2 ді U 2 ге алмастырып, белгілеп алып, А- формасының теңдеуін аламыз.

    U 1 = AU 2 + BI 2

    I 1 = CU 2 + DI 2
    Симметриялы төртұштықтың шарты: А=D

    18.4. Пассивты төртұштықтың алмасу схемасы

    Т- схемасы

    Z 1 = Z 2 = Z 3 =

    П-схемасы

    Z4 =B Z 5 = Z 6 =

    Т- схемасы


    П-схема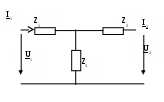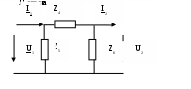

    1   2   3

    написать администратору сайта