Дискретка. Лекция 10. Лекция 10. Разбиения множеств
 Скачать 68.98 Kb. Скачать 68.98 Kb.
|
|
Лекция 10. Разбиения множеств. Цель: ознакомить студентов с видами разбиения множеств и формулами подсчета количества способов разбиения Структура лекции: 1. Формулы различных разбиений множеств. 2. Числа Стирлинга. 3.Формула включений и исключений. Под разбиением n-элементного множества на k подмножеств (блоков) понимают произвольное семейство множеств { X1, X2, …, Xk } такое, что 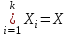 , , 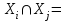 , ij Хi, i= , ij Хi, i=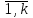 Множество всех разбиений множества Х на k блоков обозначим Пк(х). Число разбиений n-элементного множества на k блоков обозначим S(n,k)= | Пк(х)|. Очевидно, S(n, k)=0 для kn; полагается S(0, 0)=1. Утверждение 1. S(n, k)= S(n-1, k-1)+kS(n-1, k) при 0kn; S(n, n)=1 при n0 ; S(n, 0)=0 при n0. Числа S(n, k) называются числами Стирлинга II рода. Действительно, вторая и третья формулы очевидны. Для доказательства первой формулы рассмотрим множество всех разбиений множества {1, 2, …, n} на k блоков. Это множество распадается на два различных класса: тех разбиений, которые содержат одноэлементный блок {n} и тех разбиений, для которых n является элементом блока мощности больше 1. В первом классе содержатся S(n-1, k-1) блоков, а во втором - k S(n-1, k), так как каждому разбиению множества {1, 2, …, n-1} на k блоков соответствует в этом классе в точности k разбиений, образованных добавлением элемента n поочередно к каждому блоку. Например, S(4, 2) = S(3, 1) + 2S(3, 2) = 1 + 2(S(2, 1) + 2S(2, 2)) = 1 + 2(1+2) = 7. Если Х = {1, 2, 3, 4}, то семь разбиений этого множества на два блока будут иметь вид: {{1, 2, 3}, {4}} {{2, 3, 4}, {1}} {{1, 2, 4}, {3}} {{1, 2}, {3, 4}} {{1, 3, 4}, {2}} {{1, 4}, {2, 3}} {{1, 3}, {2, 4}} Числа Стирлинга II рода можно расположить в виде треугольной таблицы
Каждое число таблицы, кроме крайних, равных 1, получается как сумма числа, расположенного над вычисляемым, и умноженного на k, и числа, расположенного над вычисляемым слева от него. Подсчитаем теперь число разбиений конечного множества Х, где Х=n на k подмножеств Х1, Х2, …, Хk (k1) таких, что каждое Xi содержит ni элементов, т.е. 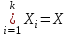 , , 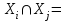 , ij Хi=ni, i= , ij Хi=ni, i=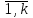 Очевидно, при этом  . Отметим, что для некоторых номеров i возможно Хi=. Число указанных разбиений при фиксированных ni обозначим . Отметим, что для некоторых номеров i возможно Хi=. Число указанных разбиений при фиксированных ni обозначим  . (Заметим, что в данном случае набор подмножеств в разбиении является упорядоченным, то есть (Х1, Х2, …, Хk)- упорядоченная последовательность множеств). . (Заметим, что в данном случае набор подмножеств в разбиении является упорядоченным, то есть (Х1, Х2, …, Хk)- упорядоченная последовательность множеств).Утверждение 2.  = = 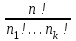 . .Действительно, каждое подмножество Хi можно рассматривать как сочетание без повторений, тогда  = = 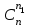 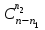  … … 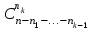 = = 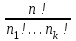 Пример. В группе из 25 человек выбирали старосту. "За" проголосовали 12 человек, "против" – 10, "воздержались" – 3. Сколькими способами могло быть проведено такое голосование? 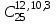 = = 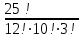 = 1487285800. = 1487285800.Теперь посчитаем, сколькими способами можно разбить множество Х, |X|=n на подмножества такие, что для каждого i=1, 2, …, n имеется mi подмножеств с i элементами ( 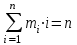 ). В отличие от предыдущего случая набор подмножеств в таком разбиений не упорядочен. Например, для множества Х = {1, 2, 3, 4, 5} следующие три разбиения считаются одинаковыми ). В отличие от предыдущего случая набор подмножеств в таком разбиений не упорядочен. Например, для множества Х = {1, 2, 3, 4, 5} следующие три разбиения считаются одинаковыми {1, 3}, {4}, {2, 5} {4}, {2, 5}, {1, 3} {2, 5}, {4}, {1, 3} В этом разбиении m1=1, m2=2, m3=m4=m5=0. Обозначим число указанных разбиений через N(m1, m2, …, mn). Утверждение 3. N(m1, m2, …, mn) =  Действительно, каждое из рассматриваемых неупорядоченных разбиений можно привести m1!m2!…mn! способами к упорядоченным разбиениям вида 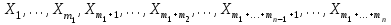 где 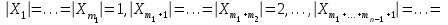 = 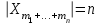 . .Число этих упорядоченных разбиений равно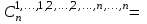 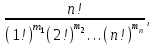 а число неупорядоченных разбиений в m1!…mn! раз меньше, что и отражается в доказываемой формуле. Пример. Сколькими способами из группы 25 человек можно сформировать 5 коалиций по 5 человек? |X| = 25, m1=…=m4=0, m5=5, m6=…=m25=0 N(0, 0, 0, 0, 5, 0, …, 0) =  = 5194672859376. = 5194672859376.Формула включений и исключений Пусть Х1, Х2 – два конечных множества. Тогда, если Х1Х2 = , то |Х1Х2| = |Х1|+|Х2|. Если Х1Х2 , тогда в |Х1|+|Х2| каждый элемент из Х1Х2 будет учтен два раза, следовательно |Х1Х2| = |Х1|+|Х2| - | Х1Х2|. Получим соответствующую формулу для произвольного числа множеств, которая называется формулой включений и исключений. Утверждение 4. Пусть Хi – конечные множества i = 1, …, n, n2. Тогда |X1X2…Xn| = (|X1| + … + |Xn|) – (|X1X2| + |X1X3| + … + |Xn-1Xn|) + (|X1X2X3| + … + |Xn-2Xn-1Xn|) - … + (-1)n+1|X1X2…Xn|. Следствие. Пусть Х – конечное множество, Х1, …, Хn – подмножества множества Х. Тогда количество элементов хХ, не принадлежащих ни одному из этих подмножеств можно вычислить по формуле: |X \ ( X1X2…Xn)| = |X| - (|X1| + … + |Xn|) + (|X1X2| + … |Xn-1 Xn|) - … - (-1)n|X1…Xn|. Наиболее распространенная форма записи формулы включений и исключений следующая. Пусть Х – конечное множество, состоящее из N элементов, а 1, …, n – некоторые свойства, которыми могут обладать или не обладать элементы из Х. Обозначим через Xi множество элементов из Х, обладающих свойством i, т.е. Хi = {xX | i(x)}, i=1, …, n. Обозначим через N( 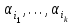 ) количество элементов из Х, одновременно обладающих свойствами ) количество элементов из Х, одновременно обладающих свойствами 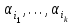 . Тогда . Тогда N( 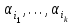 ) = | ) = |  |. |.Количество элементов, не обладающих ни одним из свойств 1, …, n N0 = | X \ (X1…Xn) |. Тогда N0 = N – S1 + S2 - … + (-1)nSn = N + 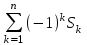 , где , где Sk =  , k=1, …, n. , k=1, …, n.Например, если n=3, то N0 = N – N(1) – N(2) – N(3) + N(1, 2) + N(1, 3) + N(2, 3) – N(1, 2, 3). Пример. Пусть Х = {1, 2, …, 10}, 1(x) : "х – четное", 2(х) : "x>6", 3(x) : "2 Рассмотрим еще одну задачу, использующую формулу включений и исключений. Задача "о беспорядках". Имеется n различных предметов а1, а2, …, an и n различных ячеек b1, b2, …, bn. Сколькими способами можно разместить предметы по ячейкам так, чтобы никакой предмет ai не попал в ячейку bi? Другая формулировка: сколько существует перестановок a1, a2, …, an чисел 1, 2, …, n
таких, что aii при любом i = 1, 2, …, n, т.е. сколько существует таких подстановок, в которых прообраз любого элемента не равен образу? В качестве исходного множества Х возьмем совокупность всевозможных расположений предметов по ячейкам. Тогда N=| X |=n! Введем свойства i: "ai находится в ячейке bi", i = 1, …, n. Число N( 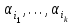 ) расположений, при которых предмет ij находится в ячейке bij j = 1, …, k равно (n-k)!. ) расположений, при которых предмет ij находится в ячейке bij j = 1, …, k равно (n-k)!.Но тогда число расположений, когда k предметов попадает в свои ячейки Sk = 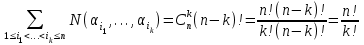  Используя теперь формулу включений и исключений получаем, что число N0 расположений, при которых ни одно свойство не выполняется (т.е. ни один предмет ai не попал в ячейку bi) равно Используя теперь формулу включений и исключений получаем, что число N0 расположений, при которых ни одно свойство не выполняется (т.е. ни один предмет ai не попал в ячейку bi) равноN0=N+ 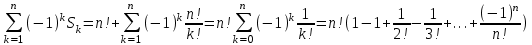 . .Заметим, что выражение в скобках – первые члены бесконечно ряда разложения е-1, следовательно 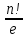 - весьма хорошее приближение для числа беспорядков из n символов. - весьма хорошее приближение для числа беспорядков из n символов.Если нас интересует не только число беспорядков, но также число перестановок а1, …, an из 1, 2, …, n для которых аi=i точно в k местах, то возникает задача "о встречах". Ее решение получается так: k чисел из n можно выбрать 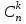 способами, а выбрав, нужно умножить на число беспорядков из оставшихся n-k символов. способами, а выбрав, нужно умножить на число беспорядков из оставшихся n-k символов.Тогда Nk = 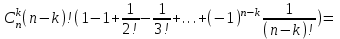   . . |
