Лекция_Методы анализа ЭМС РЭС. Лекция 11. Методы анализа эмс рэс методы анализа эмс рэс

• Название: Лекция 11. Методы анализа эмс рэс методы анализа эмс рэс
• Дата: 21.03.2019
• Размер: 279 Kb.
• Имя файла: Лекция_Методы анализа ЭМС РЭС.doc
• Тип: Лекция; #71139
• страница: 2 из 2

Расчет внеполосных характеристик антенн.

Внеполосные характеристики антенн в настоящее время не нор­мируются, не контролируются при их производстве или сертификации и не приводятся в эксплуатационной и иной технической документации. В тоже время, расчет мощности радиопомехи на входе рецептора предполагает знание коэффициента усиления антенны радиоприемника — рецептора помех в направлении антенны радиопередатчика — источника помехи на частоте помехи. Частота поме­хи может весьма существенно отличаться от рабочей частоты антенны рецептора, а при этом пространственные и энергетические характеристики антенны могут не только количественно, но и качественно отличаться от паспортных.

Для базовых станций сотовой связи обычно используют антенны, представляющие собой многоэтажные линей­ные антенные решетки панельных излучателей, с секторными диа­граммами направленности. В ряде случаев, в качестве антенн базовых станций сотовых сетей используют всенаправленные антенны (например, вибраторные излучатели) и направленные антенны (например, панельные излучатели).

По мере роста частоты диаграмма направленности (ДН) деформируется, а начиная с какого-то момента — «разваливается» (главный лепесток ДН расщепляется на несколько узких лепестков, между которыми имеются глубокие прова­лы). Эффективным вариантом расчета параметров является расчет внеполосных характеристик ан­тенны на основе имеющихся данных о ее конструкции, геометрических (электрических) размерах элементов излучающей части антенны и входящих в ее состав устройств фидерно­го тракта.

В качестве характеристики внеполосного усиления должен использоваться коэф­фициент усиления антенны как функции угловых координат на частотах, соответствующих существенным уровням возможного внеполосного приема (контролируемые частоты). В число контролируемых частот должны быть включены:

• 
  частоты, соответствующие максимумам интенсивности приема в паразитных полосах приема антенны;
  
• 
  рабочие частоты антенн, расположенных вблизи мощных источников радиопомех.
  

Излучаемая ан­тенной мощность Р_Е определится выражением: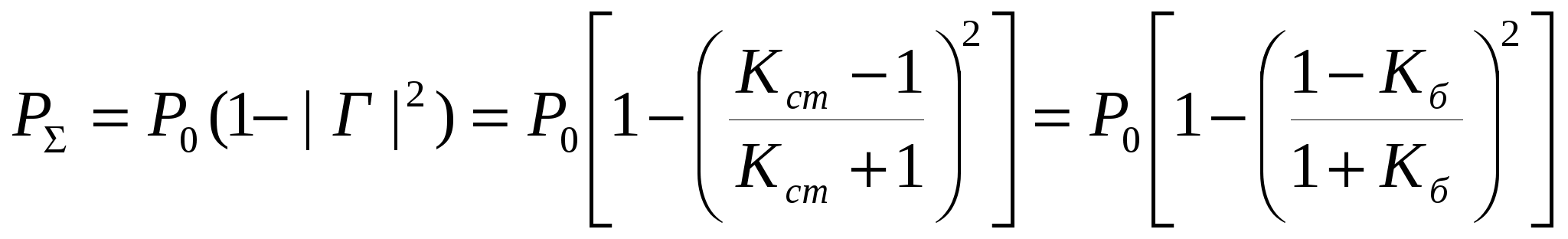

(11)

где Р₀ — мощность на входе антенны; Г, К_ст, К_б — соответственно коэффициент отражения, коэффициент стоячей волны напряжения (КСВН) и коэффициент бегущей волны (КБВ) на входе антенны. Частоты, соответствующие максимумам излучаемой антенной мощности определяются минимумами ко­эффициента отражения (минимумами КСВН, максимумами КБВ).

Общий алгоритм анализа включает следующие основные этапы :

• 
  предварительный расчет частотной характеристики входного импеданса антенны в широкой полосе частот;
  
• 
  определение контролируемых частот;
  
• 
  расчет характеристик направленности и коэффициента усиления антенны для контро­лируемых частот.
  

На рис. 1 приведены результаты расчета КБВ на входе вибратора (пунктирная кривая) и излучателя в целом (сплошная кри­вая). КБВ на входе вибратора определялся относительно сопротивления, равного резонанс­ному сопротивлению вибратора на рабочей частоте, а на входе излучателя — относительно волнового сопротивления тракта (в данном случае 50 Ом).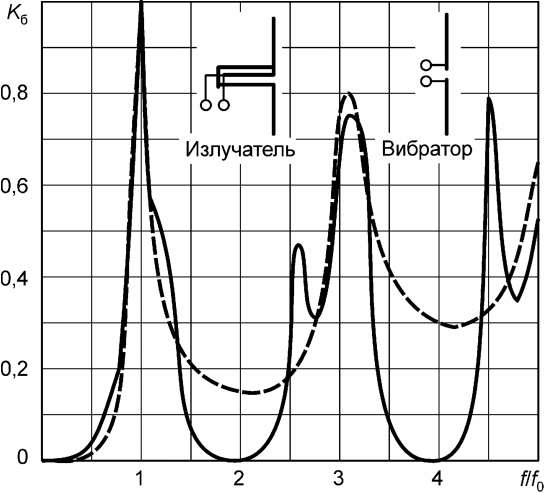



Рис. 1 Частотные характеристики входного КБВ симметричного вибратора и излучателя на его основе.

В качестве примера можно рассмотреть расчетные характеристики внеполосного коэффициента усиления четырехэтажной линейной решетки, построенной из вышеописан­ных вибраторных излучателей (общий вид решетки — на рис.2 , (а) с использованием рас­пределителя мощности 1:4 на основе четвертьволнового трансформатора, на частотах 3,2f₀ и 4,5f₀, соответствующих максимумам КБВ ( рис. 2)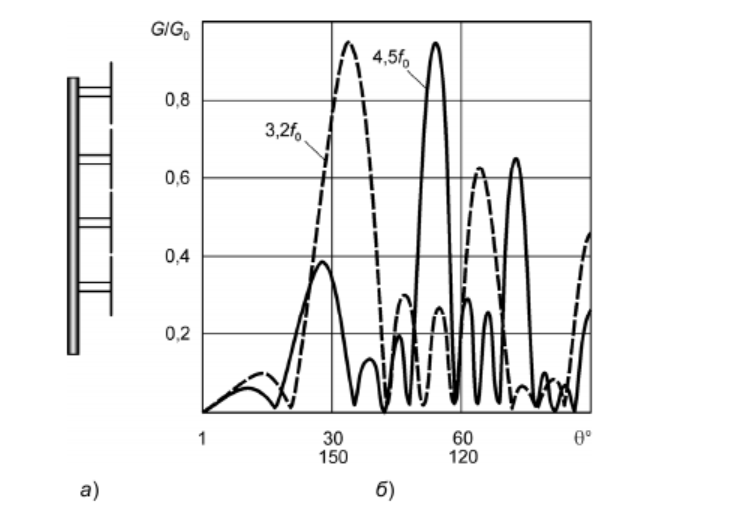



Рис. 2 Четырехэтажная линейная решетка вибраторных излучателей (а) и ее характеристика внеполосного коэффициента усиления на частотах 3,2 fo и 4,5 fo (б).

Существуют так же расчеты для пятисекционной коллинеарной антенны на четвертьволновых, четырехсекционной коллинеарной антенны Франклина – Маркони и других видов антенн.

Расчет развязки между близко расположенными антеннами.

Под близко расположенными антеннами понимаются антенны, разнесенные на относительно малое расстояние, где еще не сформированы их ДН. В таких случаях расчет развязки должен вы­полняться на основе решения соответствующей электродинамической задачи, в рамках которой определяются токи, текущие в проводниках антенн. Ниже будет рассмотрен один из исторически первых методов — метод наведенных электродвижущих сил (ЭДС), позволяющий обойтись не­большими объемами вычислений, которые вполне могут быть выполнены вручную.

Рассмотрим вопросы расчета развязки на основе электродинамического ана­лиза. Здесь можно выделить два принципиально различных подхода. В рамках пер­вого развязка определяется по напряжению, наведенному в нагрузке одной из антенн, кото­рая является пассивной, при возбуждении другой антенны. При этом требуется высокая точность решения электродинамической задачи. Второй подход предполагает определение искомых характеристик по распределению поля в дальней зоне. Последнее обладает так на­зываемыми стационарными свойствами, т.е. слабо зависит от точности определения тока, что значительно упрощает электродинамический анализ и в принципе дает возможность ис­пользовать метод наведенных ЭДС.

Рассмотрим упрощенный второй подход, позволяющий анализировать антенны с одинаковым типом поляри­зации. Это наихудший случай, так как согласованные по поляри­зации антенны сильнее взаимодействуют. Соответствующее ограничение примем и в мето­дике электродинамического анализа — ограничимся рассмотрением систем параллельных проводников.

Пусть требуется рассчитать развязку в системе двух одноэлементных антенн с од­ним типом поляризации. Будем рассматривать данную систему как четырехполюсник, вхо­дами которого являются входы антенн. Антеннам и входам присвоим номера 1 и 2. В рам­ках рассматриваемого подхода электродинамический анализ выполняется при возбуждении входов источниками тока (токи J₁ и J₂, где нижний индекс есть номер входа). Если вход ос­тается пассивным, то он может быть либо замкнут накоротко, либо разомкнут.

Электродинамический анализ выполняется для пяти режимов возбуждения:

• 
  режим 1 — возбуждение входа 1 единичным током (J₁ = 1 А) при разомкнутом входе 2;
  
• 
  режим 2 — то же при замкнутом входе 2;
  
• 
  режим 3 — возбуждение входа 2 единичным током (J₂ = 1 А) при разомкнутом входе 1;
  
• 
  режим 4 — то же при замкнутом входе 1;
  
• 
  режим 5 — противофазное возбуждение системы единичными токами
  

(J₁ = 1 А, J₂ = -1 А).

Для каждого k-го режима возбуждения решением электродинамической задачи опреде­ляется ДН f_k () как комплекснозначная функция обеих угловых сферических координат — полярного угла и азимута . Все ДН нормируются единообразно, т.е. к одному и тому же уровню, а не каждая к своему максимуму, как это принято.

Кроме того, для каждого из режимов 1, 3, 5 определяется значение напряженности элек­трического поля E_k в некоторой точке в направлении () на достаточно большом рас­стоянии R₀ (в дальней зоне). В данном направлении все ДН должны иметь ненулевые значе­ния; кроме того, для упрощения расчета поля это направление должно быть перпендикуляр­но осям проводников.

Идея метода - построение эквивалентной схемы четырехполюсника, образо­ванного системой двух антенн, и определении его коэффициента передачи, который полно­стью характеризует взаимодействие антенн, т.е. уровень их развязки. В качестве эквива­лентной схемы используется Т-образная цепь. Расчет развязки близко расположенных антенн выполняется в следую­щей последовательности:

1. 
   решение пяти электродинамических задач для пяти режимов возбуждения, указанных выше; расчет ДН f_k () и значений поля E_k;
   
2. 
   расчет мощностей излучения P₁ P₃, P₅ для режимов 1, 3, 5;
   

3. 
   расчет активных составляющих r, r_b r₂ импедансов эквивалентной схемы;
   
4. 
   расчет параметров a₁ и a₂;
   
5. 
   расчет реактивных составляющих х, х₁ х₂ импедансов эквивалентной схемы;
   
6. 
   расчет Z-параметров эквивалентной схемы;
   
7. 
   расчет рабочего ослабления.
   

В большинстве случаев ДН как функцию двух переменных (углов ) с достаточной точностью можно представить в виде произведения двух ДН — в вертикальной и в горизон­тальной плоскостях, каждая из которых является функцией только одной переменной.

Все элементы антенной системы должны представлять собой прямолинейные цилиндрические проводники, электрически тонкие, т.е. имеющие радиус, значительно меньший длины волны. Каждый элемент характеризу­ется своим током, который требуется найти (за исключением активных вибраторов с за­данными токами). В нашем случае, все проводники должны быть па­раллельны.

Активный вибратор представляет собой прямолинейный проводник с узким зазором в средней точке, к которому подводится питающее напряжение. В данном случае вибратор может быть:1. возбужден (в зазоре — источник тока)- ток задан, т. е. известен и не входит в число искомых величин, 2. замкнут накоротко (зазор отсутствует), 3. разомкнут (зазор присутствует, но в нем нет никаких источников). Если вибратор

- замкнут, то он рассматривается просто как прямолинейный проводник.

- ра­зомкнут, то он рассматривается как пара прямолинейных проводников, разделенных зазо­ром.

В анализируемой системе может быть либо один возбужденный вибратор (режимы возбуждения 1-4), либо два (режим 5). Построение электродинамической модели иллюстрируется на рис. 3, где в качестве примера показана система, содержащая следующие элементы: разомкнутый вибратор (рас­сматриваемый как два проводника), пассивный элемент, активный возбужденный вибратор. Проводники условимся нумеровать всегда таким образом, чтобы возбужденные вибраторы (один или два) имели наибольшие номера. Число неизвестных токов обозначим N, при этом номера проводников, не являющихся возбужденными вибраторами, будут 1, 2, ..., N, номе­ра возбужденных вибраторов — N + 1, N + 2 (при одном возбужденном вибраторе — только N + 1). Для определения пространственной формы анализируемой структуры вводится базовая декартова система координат и для каж­дого n-го проводника задаются следующие параметры: r_n — радиус-вектор средней точки; l_n — длина; a_n — радиус. Кроме того, для указания направления проводников задается орт (единичный вектор) l₀. Так как проводники параллельны, их направления совпадают, и дос­таточно задать только один такой орт.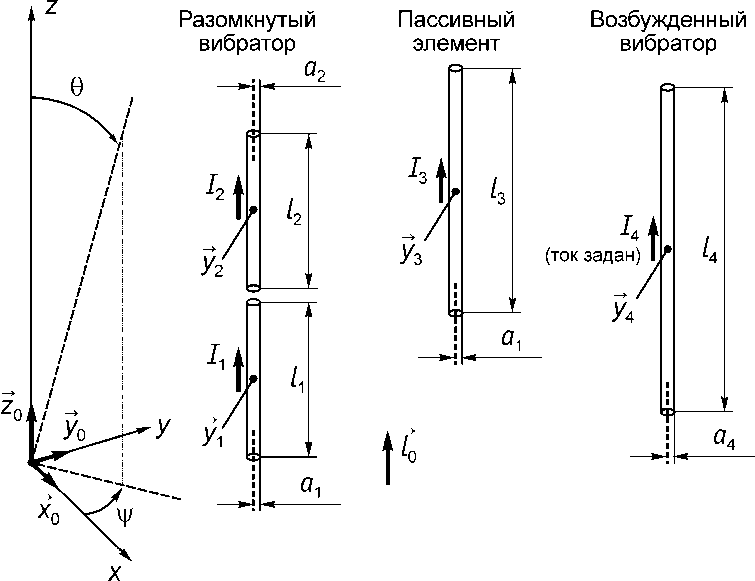





Рис. 3 Построение электродинамической модели
Токи проводников обозначим I_n (в нашем примере n = 1, 2, 3, 4). Направления токов со­ответствуют направлению орта l₀. В качестве тока возбужденного вибратора I₄ берется ток источника, равный ± 1 А в зависимости от режима возбуждения, как это указывалось выше. Как уже отмечалось, все ДН (т.е. для всех пяти режимов возбуждения) нормируются единообразно. Рекомендуется выполнять нормировку к максимальному значению той не­нормированной ДН, у которой это значение является наибольшим важно только, чтобы нормировка выполнялась единообразно для всех ДН. Значение поля в дальней зоне E_k, на расстоянии R₀, соответ­ствующее k-му режиму возбуждения.

После расчета значений E_k электродинамический анализ завершается, и далее выполня­ется расчет развязки. Вышерассмотренная задача решалась с помощью упрощенного варианта методики расчета развязки, позволяющего анализировать только антенны с одним типом по­ляризации, так, что анализируемая система содержит только параллельные проводники.

Для обеспечения высокой точности расчетов необходимо использовать мощные современные методы, основанные на решении интегральных уравнений.