НСАУ+Лекция+11 (1) (1). Лекция 11 устойчивость нелинейных систем. Методы ляпунова
 Скачать 32.05 Kb. Скачать 32.05 Kb.
|
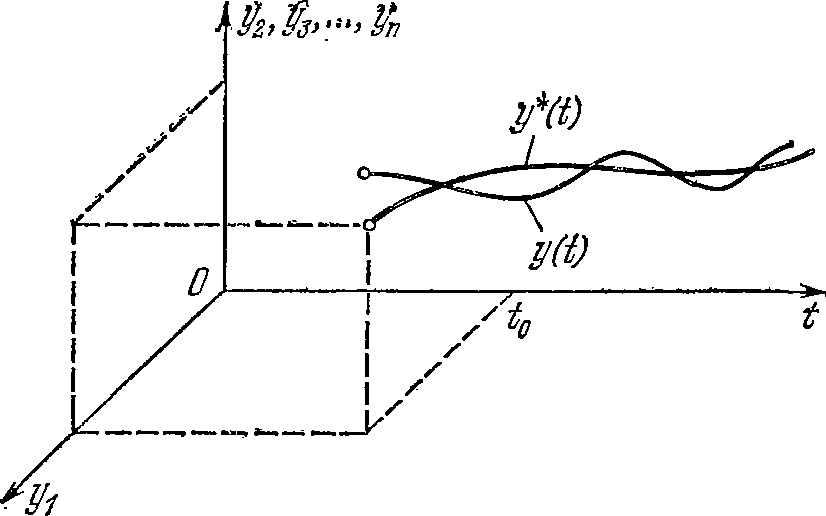
x= 0 (на рисунке 6.2 x=0 )НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ. ЛЕКЦИЯ 11 УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ. МЕТОДЫ ЛЯПУНОВА Устойчивость относится к основным свойствам динамической системы, определяющим ее общую работоспособность. Мы уже рассматривали, что такое устойчивость. Напомним, что под устойчивостью понимают свойство системы самостоятельно возвращаться к равновесному состоянию после снятия возмущения, нарушившего ее равновесие. Устойчивость линейных систем является внутренним свойством этих систем и не зависит от внешних воздействий. Поэтому для линейных систем данного определения достаточно. Как мы уже говорили, устойчивость нелинейных систем, помимо свойств системы, зависит также от состояния системы и от характера ее внешних воздействий. Все это требует более подробного изучения концепций устойчивости нелинейных систем. Это следующие понятия: устойчивость по Ляпунову, асимптотическая устойчивость, абсолютная устойчивость и некоторые другие. Для исследования устойчивости нелинейных систем применяются первый и второй методы Ляпунова, а также ряд других подходов, построенных на основе методов Ляпунова. Это мы сейчас кратко рассмотрим. Материал непростой, поэтому для хорошего усвоения от студента здесь потребуются самостоятельные занятия. Основные понятия. Первый метод Ляпунова Рассмотрим сначала определение устойчивости по Ляпунову. Рассмотрим поведение динамической системы при отсутствии или постоянстве (что то же самое) внешних воздействий x˙ f(x) , (6.1) где x – вектор переменных состояния в фазовом пространстве; f – некоторая вектор-функция. Обозначим через x*(t) некоторый установившийся процесс системы (6.1). Этот процесс называется невозмущенным движением. Таким образом, установившийся процесс движения системы при отсутствии внешних воздействий называется невозмущенным движением. Теперь предположим, что внешние воздействия изменили начальное состояние системы x(0). Это соответствует воздействию внешних факторов до нулевого времени и снятию этих воздействий в нулевой момент. То есть систему "сдвинули" в нулевой момент и затем предоставили самой себе. Движение системы после изменения ее начального состояния называется возмущенным движением. Таким образом, свободное движение системы после изменения ее начального состояния называется возмущенным движением. Обозначим возмущенное движение, как и в (6.1), через x(t). Ясно, что возмущенное движение будет отличаться от невозмущенного. Обозначим это отклонение через x, то есть x x(t) x* (t) . (6.2) Тогда можно записать уравнение возмущенного движения для отклонения x˙ F(x) , (6.3) где F – некоторая вектор-функция. Невозмущенным движением для системы (6.3) будет x= 0. Геометрически рассмотренные движения можно представить в n–мерном пространстве состояний с добавлением оси времени в виде некоторых интегральных кривых. Для изобразится прямой, совпадающей с осью времени. Другие построения на рисунке будут пояснены позже. 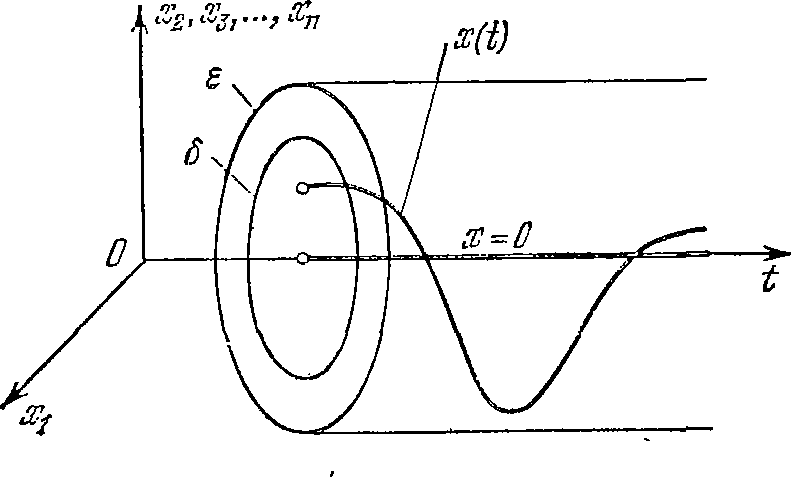 Рисунок 6.2 – Невозмущенное x= 0 и возмущенное x(t)движение системы в отклонениях от невозмущенного режима Теперь рассмотрим определение устойчивости по Ляпунову. Невозмущенное движение системы |