12 КРИВЫЕ ВТОРОГО ПОРЯДКА.ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА. (1). Лекция 12 кривые второго порядка. Поверхности второго порядка. План лекции Введение
 Скачать 391.29 Kb. Скачать 391.29 Kb.
|
|
Лекция №12 КРИВЫЕ ВТОРОГО ПОРЯДКА. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА. План лекции Введение. Канонические формы уравнений кривых второго порядка. Канонические формы уравнений поверхностей второго порядка. Кривые второго порядка (эллипсис, гипербола, парабола) как конические сечения были известны математикам д. Греции. С помощью этих кривых решались некоторые задачи на построение (удвоение куба и др.), оказавшиеся недоступными при использовании циркуля и линейки. Дальнейшие успехи в теории кривых второго порядка связаны с созданием в 17 в. нового геометрического метода - метода координат. Кривые второго порядка часто встречаются в различных явлениях природы и в человеческой деятельности. В науке они приобрели особое значение после того, как немецкий астроном И.Кеплер открыл из наблюдений, а английский ученый И.Ньютон теоретически обосновал закон движения планет, один из которых утверждает, что планеты и кометы Солнечной системы движутся по коническим сечениям, в одном из фокусов которых находится Солнце. Следующие примеры относятся к отдельным типам конических сечений: параболу описывает камень, брошенный наклонно к горизонту; в некоторых механизмах пользуются зубчатыми колесами эллиптической формы; гипербола служит графиком обратной пропорциональности. Такие многообразные применения имеют и поверхности второго порядка. Кривые второго порядка. Канонические формы уравнения кривых второго порядка. Определение 1. Кривой второго порядка называется множество точек 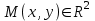 , удовлетворяющих уравнению , удовлетворяющих уравнению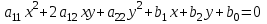 (1) (1)Канонические уравнения кривых второго порядка. Эллипсис (рис.1а)  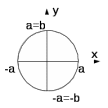 А) Б) Рис.1  -центрально-симметричная ограниченная кривая, пересекающая оси координат в точках -центрально-симметричная ограниченная кривая, пересекающая оси координат в точках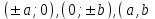 - полуоси - полуоси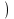 . При . При  получаем уравнение окружности (рис.1б): получаем уравнение окружности (рис.1б):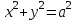 . .Если положить 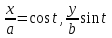 получим параметрическое уравнение эллипса: 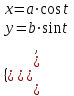  Характеристическое свойство эллипса: эллипсом называется геометрическое место точек 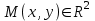 , сумму расстояний которых от двух данных точек , сумму расстояний которых от двух данных точек 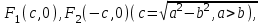 называемых фокусами, есть постоянное число, равное называемых фокусами, есть постоянное число, равное 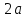 : :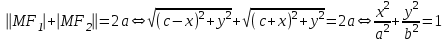 2) Гипербола 2) Гипербола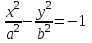 - центрально-симметричная неограниченная кривая, пересекающая ось Оx в точках - центрально-симметричная неограниченная кривая, пересекающая ось Оx в точках 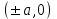 , ветви которой приближаются при , ветви которой приближаются при  к двум прямым к двум прямым 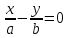 и и 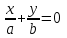 , называемыми асимптотами гиперболы (рис.2). , называемыми асимптотами гиперболы (рис.2).  Рис.2 Рис.3 Характеристическое свойство гиперболы: гиперболой называется геометрическое место точек 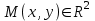 , модуль разности каждой из которых до двух фиксированных точек , модуль разности каждой из которых до двух фиксированных точек 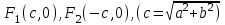 , называемых фокусами, постоянен и равен , называемых фокусами, постоянен и равен 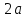 . .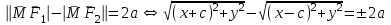 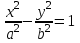 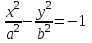 -сопряженная гипербола (рис.3). -сопряженная гипербола (рис.3).3) Парабола 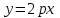 - симметричная относительно оси - симметричная относительно оси  , неограниченная кривая с вершиной в точке (0,0) (рис.4) , неограниченная кривая с вершиной в точке (0,0) (рис.4)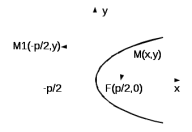 Характеристическое свойство параболы: параболой называется геометрическое место точек 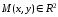 , равноудаленных от фиксированной точки , равноудаленных от фиксированной точки 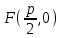 , называемой фокусом, и фиксированной прямой , называемой фокусом, и фиксированной прямой 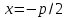 , называемой директрисой: , называемой директрисой: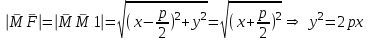 4 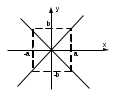 ) Пара пересекающихся прямых ) Пара пересекающихся прямых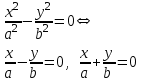 5) Пара параллельных прямых  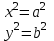 6) Пара совпадающих прямых  - ось - ось 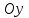 , , 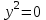 - ось - ось  7) Точка 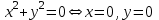 8) Пустое множество 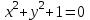 3. Поверхности второго порядка. Канонические уравнения поверхностей второго порядка. Определение 2. Поверхности второго порядка называется множество всех точек 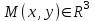 , удовлетворяющих уравнению , удовлетворяющих уравнению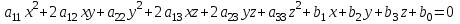 Канонические уравнения поверхностей второго порядка. 1) Эллипсоид  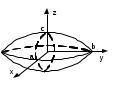 –центрально-симметричная, ограниченная поверхность, пересекающая оси координат в точках –центрально-симметричная, ограниченная поверхность, пересекающая оси координат в точках 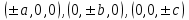 , лежащая в прямоугольном параллелепипеде , лежащая в прямоугольном параллелепипеде Все плоские сечения эллипсоида - эллипсы. При 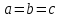 получается уравнение сферы получается уравнение сферы 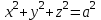 2) Гиперболоиды  а)  – однополостный гиперболоид, неограниченная, центрально-симметричная поверхность. Плоскости – однополостный гиперболоид, неограниченная, центрально-симметричная поверхность. Плоскости  пересекают его по эллипсам, плоскости пересекают его по эллипсам, плоскости 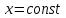 и и 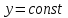 – по гиперболам. Поверхность гиперболоида можно составить из прямых. Это свойство было использовано инженером Шуховым при строительстве Московской телебашни. – по гиперболам. Поверхность гиперболоида можно составить из прямых. Это свойство было использовано инженером Шуховым при строительстве Московской телебашни.б 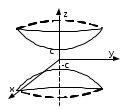 ) )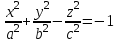 – двуполостный гиперболоид, неограниченная, центрально-симметричная поверхность. Плоскости – двуполостный гиперболоид, неограниченная, центрально-симметричная поверхность. Плоскости  пересекают его по эллипсам, плоскости пересекают его по эллипсам, плоскости 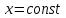 , ,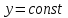 - гиперболам. - гиперболам.3) Параболоиды а) 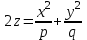 - эллиптический параболоид - эллиптический параболоид  , неограниченная пов , неограниченная пов ерхность с осью симметрии ерхность с осью симметрии  , расположенная в полупространстве , расположенная в полупространстве  . Сечения эллиптического параболоида плоскостями . Сечения эллиптического параболоида плоскостями 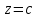 - эллипсы, а - эллипсы, а 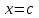 и и 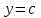 – параболы. – параболы.б)  - гиперболический параболоид, неограниченная поверхность с осью симметрии - гиперболический параболоид, неограниченная поверхность с осью симметрии 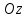 . Сечения гиперболического параболоида плоскостями . Сечения гиперболического параболоида плоскостями 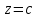 – гиперболы, а – гиперболы, а 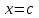 и и 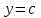 – параболы. – параболы.4) Конус  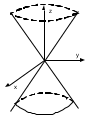 - неограниченная центрально-симметричная поверхность с центром в начале координат. Сечения конуса плоскостями - неограниченная центрально-симметричная поверхность с центром в начале координат. Сечения конуса плоскостями 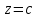 - эллипсы, - эллипсы,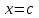 , ,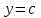 - гиперболы. - гиперболы.5) Пара пересекающихся плоскостей 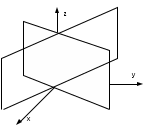 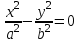  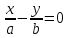 Или 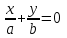 6  ) Пара параллельных плоскостей ) Пара параллельных плоскостей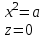 7) Пара совпадающих плоскостей  8) Цилиндры Поверхность называется цилиндрической, если она получена движением прямой (образующей) параллельно фиксированной прямой по плоской кривой (направляющей).  - уравнение цилиндрической поверхности с образующей, параллельной оси - уравнение цилиндрической поверхности с образующей, параллельной оси 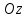 и направляющей, лежащей в плоскости и направляющей, лежащей в плоскости 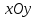 и задаваемой уравнением и задаваемой уравнением  а  ) ) - эллиптический цилиндр - эллиптический цилиндрб) 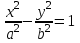 - гиперболический цилиндр - гиперболический цилиндр в)  - параболический цилиндр - параболический цилиндр 9) Прямая 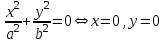 -ось -ось  10) Точка 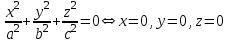 - начало координат - начало координат11)Пустое множество 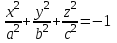 или или 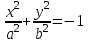 Кривыми и поверхностями, рассмотренными в этой лекции, исчерпываются все кривые и поверхности второго порядка. |
