ЛЕКЦИЯ 13. Лекция 13 верификация, тестирование и оценивание корректности программных компонентов
 Скачать 200.7 Kb. Скачать 200.7 Kb.
|
0,01. Поэтому оценивание стратегий тестирования и достигаемой при этом корректности целесообразно проводить в диапазоне qi}= 0,1—0,01, соответствующем практически наихудшим и наилучшим значениям вероятностей ошибок в дуге до тестирования.13.5. Примеры оценок сложности тестирования программ Приведенные выше выражения можно использовать для априорной оценки числа маршрутов и сложности тестирования (необходимого числа тестов для охвата всех выделенных маршрутов) программных модулей. Для планирования тестирования необходимо выявить зависимости этих характеристик от числа операторов в программе, ее структуры и критериев выделения маршрутов. Эту задачу можно решать экспериментально, путем подсчета соответствующих характеристик в реальных программных модулях, используемых в различных классах ПС. Для выявления общих зависимостей сложности тестирования программ целесообразно выделить типовые программные структуры, а также такие, которые позволяют получить предельные (сверху и снизу) значения этих характеристик. На рис. 13.7 представлен пример исходного графа модуля программы, содержащего 14 вершин, 20 дуг и 3 цикла. Такая программа сравнительно невысокой сложности содержит около 30—50 операторов на языке высокого уровня и может рассматриваться как достаточно типичная. Для полной проверки модуля по первому критерию достаточно четырех маршрутов. По этому критерию гарантируется проверка всех передач управления между операторами программы и каждого оператора не менее одного раза. Самый длинный по числу вершин маршрут не охватывает только 3 вершины из 14 и только 6 дуг из 20. После проверки еще двух маршрутов вне контроля остаются одна вершина и две дуги. Однако при этом критерии не учитывается комбина- 401 Лекция 13. Верификация, тестирование и оценивание корректности компонентов Рис. 13.7 402 торика сочетания условий на разных участках маршрутов, например, при сочетаниях направлений ветвлений в вершинах 3 и 12. Сложность программы при выделении маршрутов по этому критерию характеризуется числом маршрутов равным четырем и сложностью тестирования равной 20. Эта величина характеризует суммарное число условий, которое необходимо задать в тестах для полной проверки всех маршрутов, выделенных по первому критерию. Условия в вершинах каждого маршрута могут использоваться для автоматизированного формирования предикатов в соответствующих тестах. 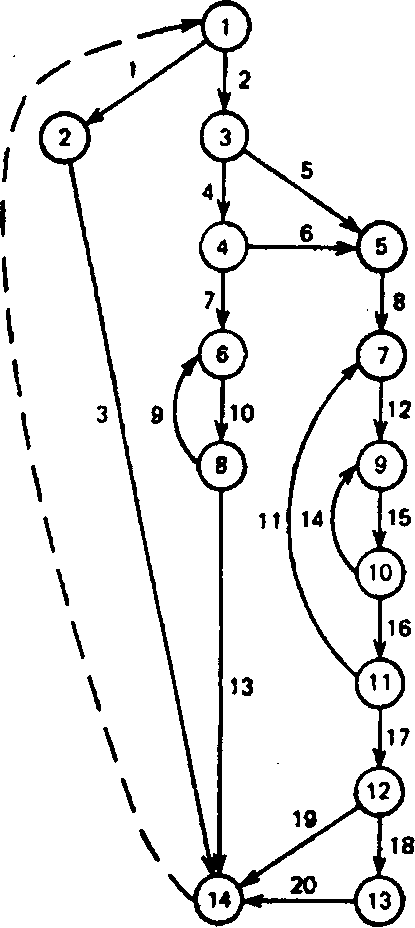 13.5. Примеры оценок сложности тестирования программ Второй критерий выбора маршрутов при оценке сложности тестирования обеспечивает в исходном графе программы однократную проверку каждого линейно независимого ациклического маршрута и каждого линейно независимого цикла, в совокупности образующих базовые маршруты. Каждый линейно независимый маршрут или цикл отличается от всех остальных хотя бы одной вершиной или дугой. Этот критерий наиболее полно исследован при анализе корреляции сложности и трудоемкости создания программ. Множество проверяемых по этому критерию структур образуется из трех линейно независимых циклов и пяти линейно независимых ациклических структур. При этом суммарная сложность тестов, учитывающих все условия прохождения маршрутов один раз, становится равной 25. Наиболее глубокий третий критерий проверки и определения сложности тестирования структуры программы включает требования однократной проверки не только линейно независимых, но и всех линейно зависимых циклов и ациклических маршрутов. Он заключается в анализе хотя бы один раз каждого из реальных ациклических маршрутов исходного графа программы и каждого цикла, достижимого из всех этих маршрутов. Для примера графа программы, представленного на рис. 13.7, по данному критерию необходимо исполнить 6 ациклических и 5 маршрутов, из которых достижимы элементарные циклы. Для реализации выделенных маршрутов в 11 тестах необходимо в совокупности задать 66 условий. При этом особенностью четырех последних маршрутов с циклами, так же как соответствующих им ациклических маршрутов, является полный перебор сочетаний ветвлений в 3 и 12 вершинах. В реальных программах некоторые маршруты могут оказаться нереализуемыми из-за несовместимости условий, которые последовательно анализируется в разных вершинах (например, вершины 3 и 12 на рис. 13.7). С другой стороны, для каждого реализуемого маршрута может быть необходимой проверка при нескольких прохождениях циклов и нескольких значениях каждой обрабатываемой переменной. Особенно важно проверять циклы с условным выходом на одном-двух промежуточных, а также при максимальном и минимальном числе витков исполнения циклов. В результате показатель сложности, число необходимых тестов и длительности проверки соответственно возрастают. 403 Лекция 13. Верификация, тестирование и оценивание корректности компонентов Для выявления основных закономерностей и оценки предельных характеристик структурной сложности тестирования ПМ проведен анализ характеристик качества тестирования абстрактных ациклических программных модулей и представительной выборки реальных модулей сложных ПС. Исследование реальных ПМ показало, что более половины из них не содержат циклов, что позволило сосредоточить на них внимание. Предполагалось, что после тестирования по любому маршруту каждой дуги графа программы вероятность наличия ошибки в этой дуге равна нулю. Ветвления в программах объектных ЭВМ происходят через 5—10 операторов текста программ, поэтому число маршрутов исполнения ациклических ПМ пропорционально их объему, выраженному числом строк текста программ. Анализ проведен для двух типов ациклических графов при выделении маршрутов по критерию охвата каждой дуги графа программы хотя бы один раз Xt и по критерию выделения всех маршрутов, различающихся хотя бы одной дугой Х2. В числе выбранных содержатся структуры, охватывающие наиболее типовые варианты компонентов графов программ. Структуры различались шириной графов, вследствие чего отличались число маршрутов и сложность полного тестирования таких структур. Сложность тестирования ПМ оценивалась по числу маршрутов исполнения программы, отражающих число тестов, необходимых для полной проверки корректности структуры модуля. Кроме того, в качестве показателя структурной сложности тестирования анализировалось суммарное число условий, которое необходимо задать в тестах (сложность тестирования) для проверки модуля. Граф Tj представлял собой симметричное упорядоченное бинарное дерево с максимальным использованием различных ветвлений и максимальной шириной. В графе Г2, наоборот, ширина минимальная и всего два полностью различающихся маршрута. При выделении маршрутов по первому критерию в графе Г2 только два маршрута и не зависят от числа вершин ветвления. В графе Г{при выделении маршрутов по первому критерию их число линейно возрастает при увеличении числа вершин. При выделении маршрутов по второму критерию их число пропорционально полному числу вершин для этих типов графов. Структурная сложность тестирования графов ПМ изменяется в более широком диапазоне, чем число маршрутов, что определило выбор 404 13.5. Примеры оценок сложности тестирования программ логарифмического масштаба по оси ординат на рис. 13.8. Наименьшей структурной сложностью характеризуется граф Г2 при выделении маршрутов по первому критерию. Для таких графов структурная сложность возрастает практически линейно в зависимости от числа вершин. При выделении маршрутов по второму критерию тот же граф характеризуется наибольшей структурной сложностью. При 30 и более вершинах структурная сложность этого графа почти на порядок выше, чем графа Г{при том же числе вершин. Относительная разница сложности тестирования этих графов при критерии Х2 приблизительно сохраняется при изменении числа вершин от 16 до 100. Такое распределение значений структурной сложности от типов графов обусловлено различием их ширины. Так как число маршрутов при критерии Х2 в зависимости от числа вершин во всех графах изменяется практически одинаково, то определяющим различия структурной сложности является число условий, анализируемых в каждом маршруте. Во всех маршрутах графа Г2 участвуют все его вершины, что определило его наибольшую структурную сложность. 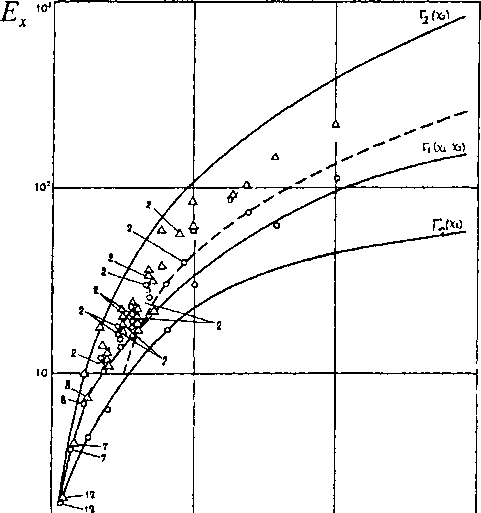 О 10 20 30 ^В Рис. 13.8 На рис. 13.8 точками (с указанием числа совпадающих значений) отмечены значения структурной сложности тестирования около 70 реаль- 405 Лекция 13. Верификация, тестирование и оценивание корректности компонентов ных ациклических ПМ в двух системах. Характеристики абстрактных графов Tj и Г2 действительно охватывают диапазон изменения показателей сложности тестов для реальных программ, которые по каждому критерию группируются приблизительно посередине. Максимальная сложность тестов по второму критерию для произвольных ациклических программ близка к числу вершин в квадрате. По тому же критерию минимальная сложность тестов для широких структурированных графов типа «дерево» на порядок меньше максимальной сложности. Для усредненных оценок сложности полных тестов произвольных ациклических программ хорошее приближение для инженерных оценок при пъ> 10 дает выражение пъ2/3(штриховая линия на рис. 13.8). Характерно, что увеличение числа вершин в 4 раза (от 32 до 128) для рассмотренных графов приводит к возрастанию структурной сложности более чем в 10 раз. Если же программу, имеющую 128 вершин, разделить на 4 модуля, то их суммарная сложность практически равна только учетверенной сложности модулей, содержащих по 32 вершины. Исследованные реальные ПМ 80% случаев содержат не более 10 вершин и имеют структурную сложность тестирования < 50. Показано, что при разработке ПМ целесообразно учитывать рациональное ограничение размеров модулей на уровне трехсот строк текста, что соответствует приблизительно тридцати альтернативам в ациклических программах. При этом для полного покрытия таких ПМ тестами необходимо задавать до 1000 условий, что обычно достаточно трудно или невозможно реализовать практически. В среднем полное тестирование программ с 30-ю вершинами ветвления производится тестами с суммарной сложностью около 300—500. Суммарная сложность тестов, необходимых для полного тестирования программ, имеющих различные структуры, может отличаться в несколько раз. Поэтому при разработке ПМ рекомендован рациональный размер программ модулей в пределах 100—200 строк текста, для полного тестирования которых достаточно использовать 10—20 тестов с суммарным числом условий ветвления до 100. При превышении рекомендуемых размеров ПМ их трудно протестировать полностью и целесообразно делить на более мелкие компоненты, доступные для практически полного покрытия тестами. Для получения практических оценок достигаемой корректности программы при покрытии тестами ее структуры необходимо оценить диапа- 406 13.5. Примеры оценок сложности тестирования программ зон реальной вероятности ошибки, допускаемой квалифицированным программистом первично в каждой дуге графа программы. Экспериментально установлено, что для слабо структурированных программ число ошибок, выявляемых в процессе тестирования программных модулей, составляет около одного процента числа строк текста этих модулей. Для программ обработки информации и управления число условных переходов составляет около 10% числа строк в программе, т.е. ветвление в программе происходит в среднем после исполнения 10 строк текста линейных участков. Следовдтельно, порядка 10% линейных участков (или дуг в графе) программных модулей могут содержать первоначально ошибки перед тестированием, что соответствует вероятности qi} |
