|
|
Лекция 14. Непрерывность функции. Лекция 14. Непрерывность функции. 14 Определения непрерывности функции. Определение 14. 1
Лекция 14. Непрерывность функции.
14.1. Определения непрерывности функции.
Определение 14.1. Функция 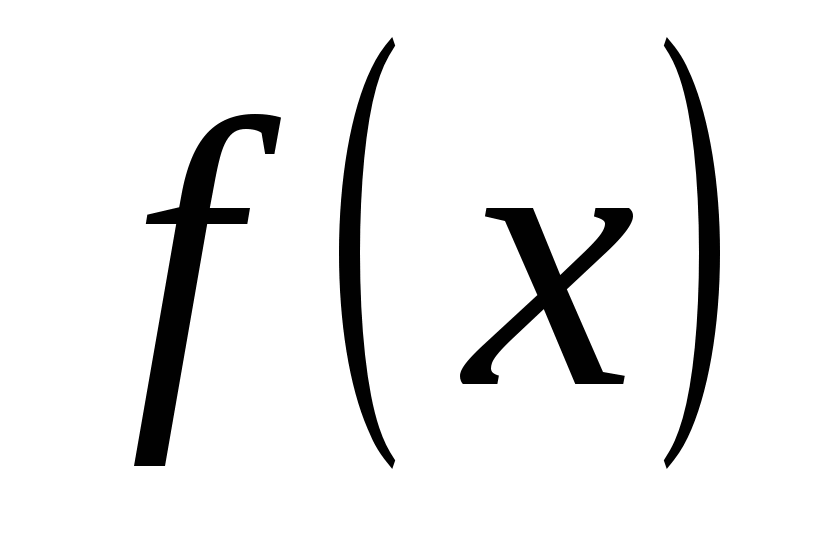 называется непрерывной в точкеa, если она удовлетворяет следующим трём условиям: называется непрерывной в точкеa, если она удовлетворяет следующим трём условиям:
1) 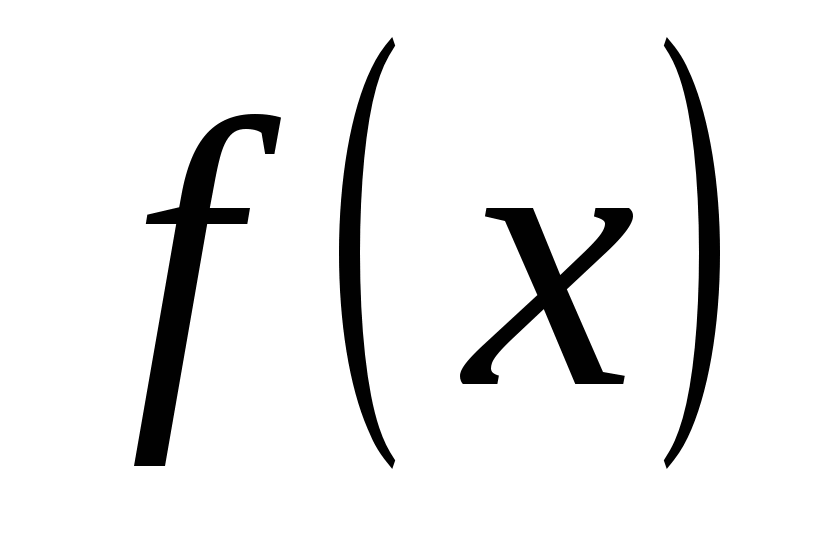 определена в точке а (то есть существует определена в точке а (то есть существует 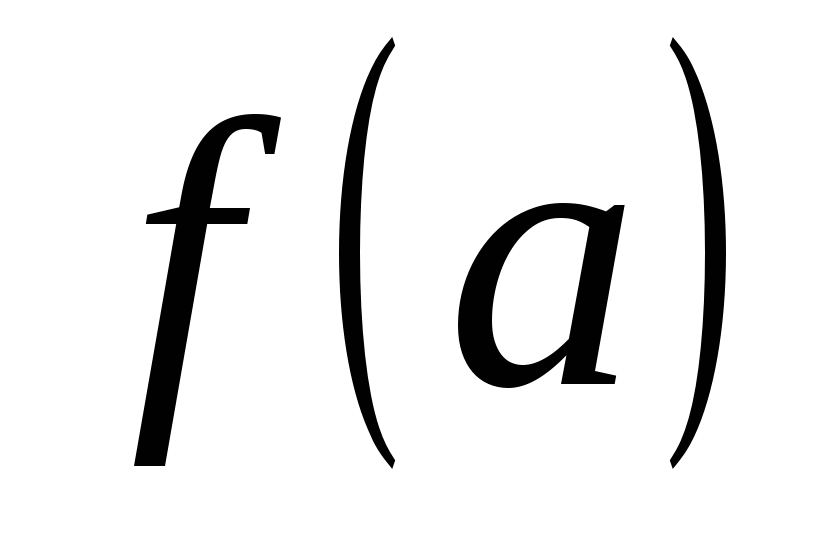 ); );
2) 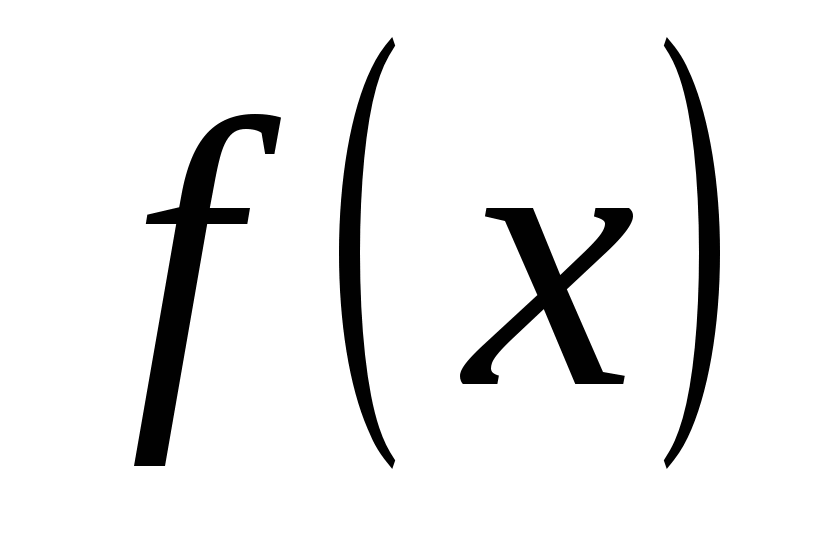 имеет конечный предел функции при имеет конечный предел функции при  ; ;
3) этот предел равен частному значению функции в точке а, то есть 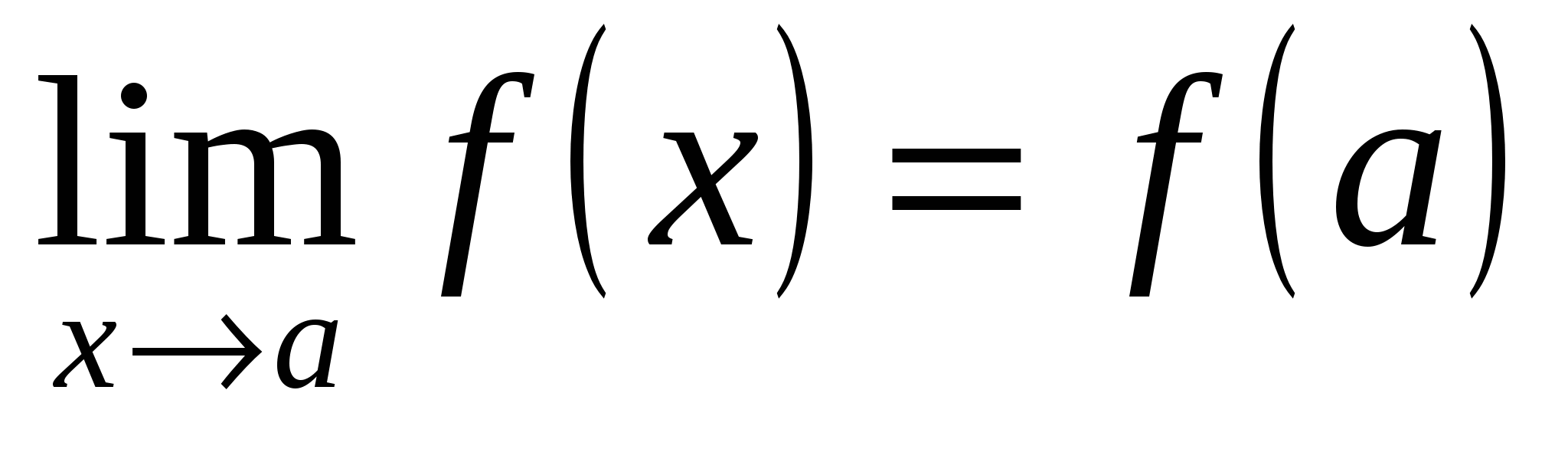 . .
Определение 14.2. Функция 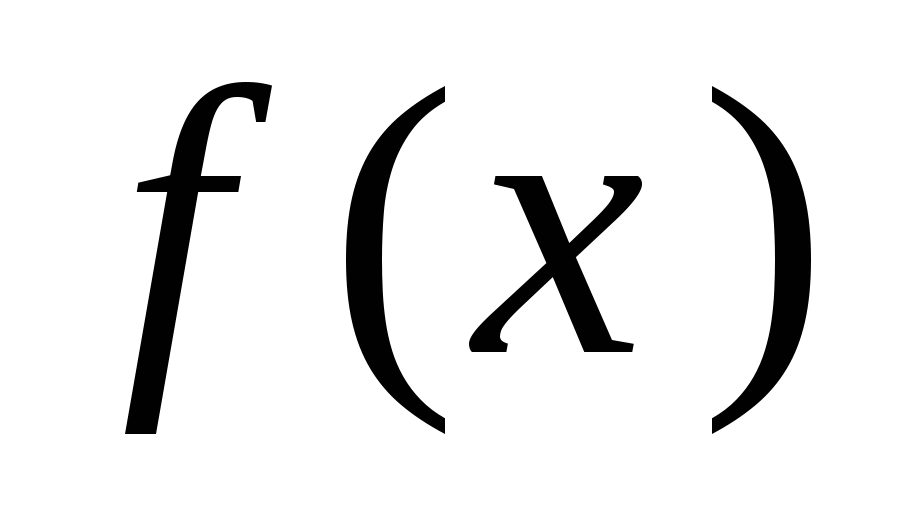 называется непрерывной справа (слева) в точкеa, если правое (левое) предельное значение этой функции в точке a существует и равно частному значению называется непрерывной справа (слева) в точкеa, если правое (левое) предельное значение этой функции в точке a существует и равно частному значению 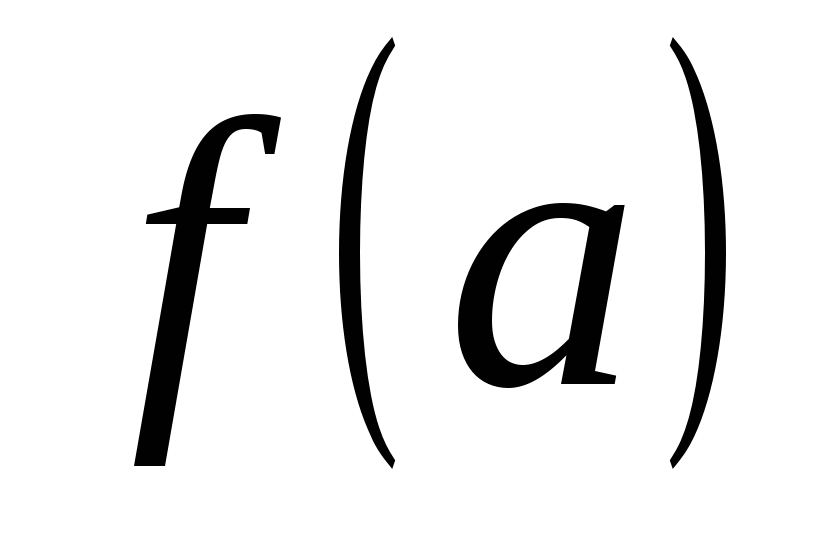 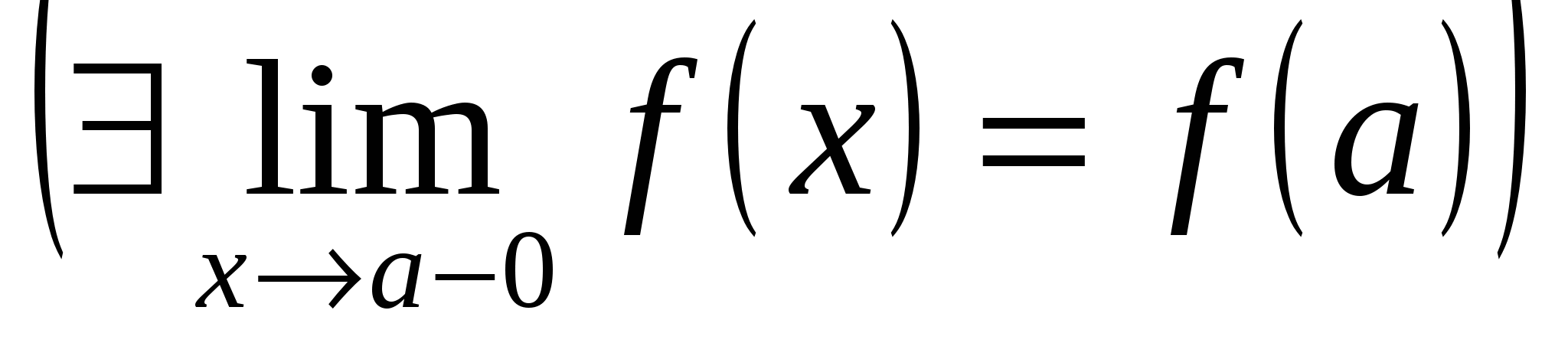 . .
Пример 14.1.
Приведём примеры непрерывных функций:
1) 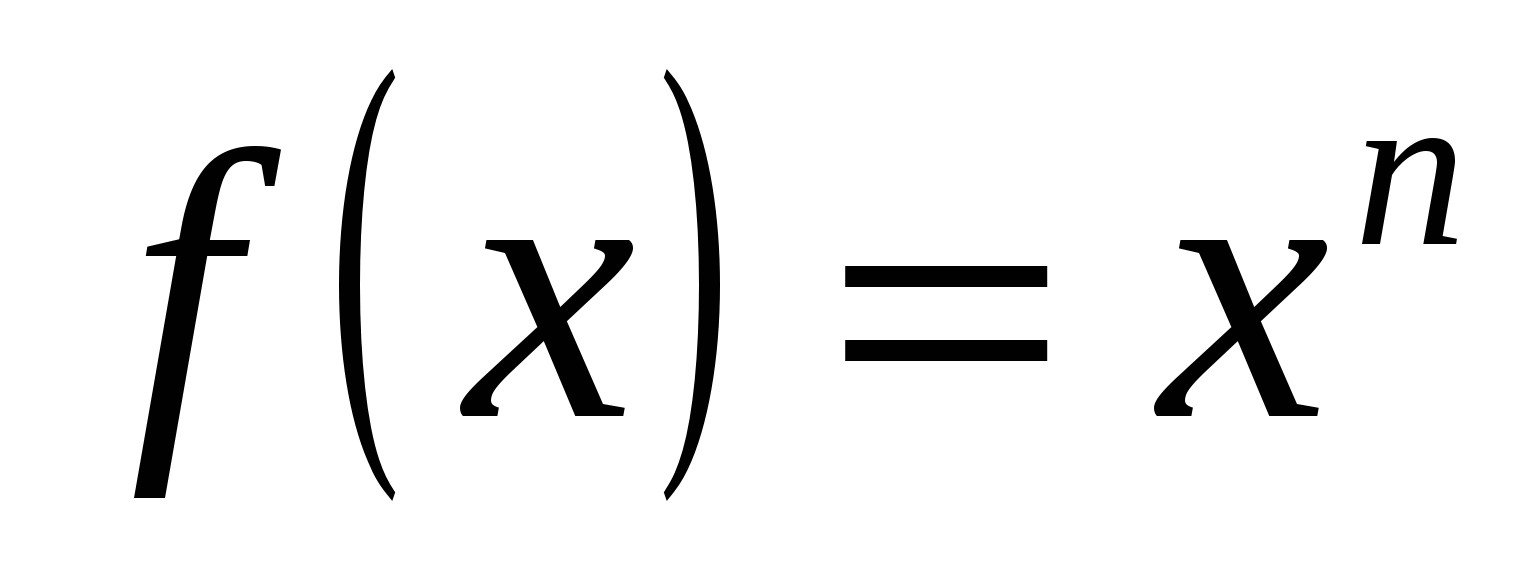 , так как , так как 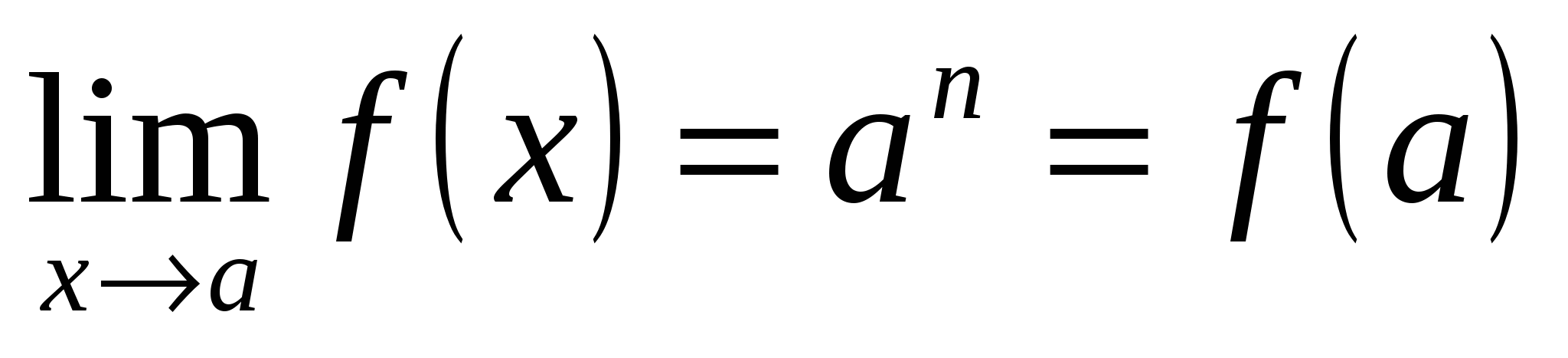 . .
2) 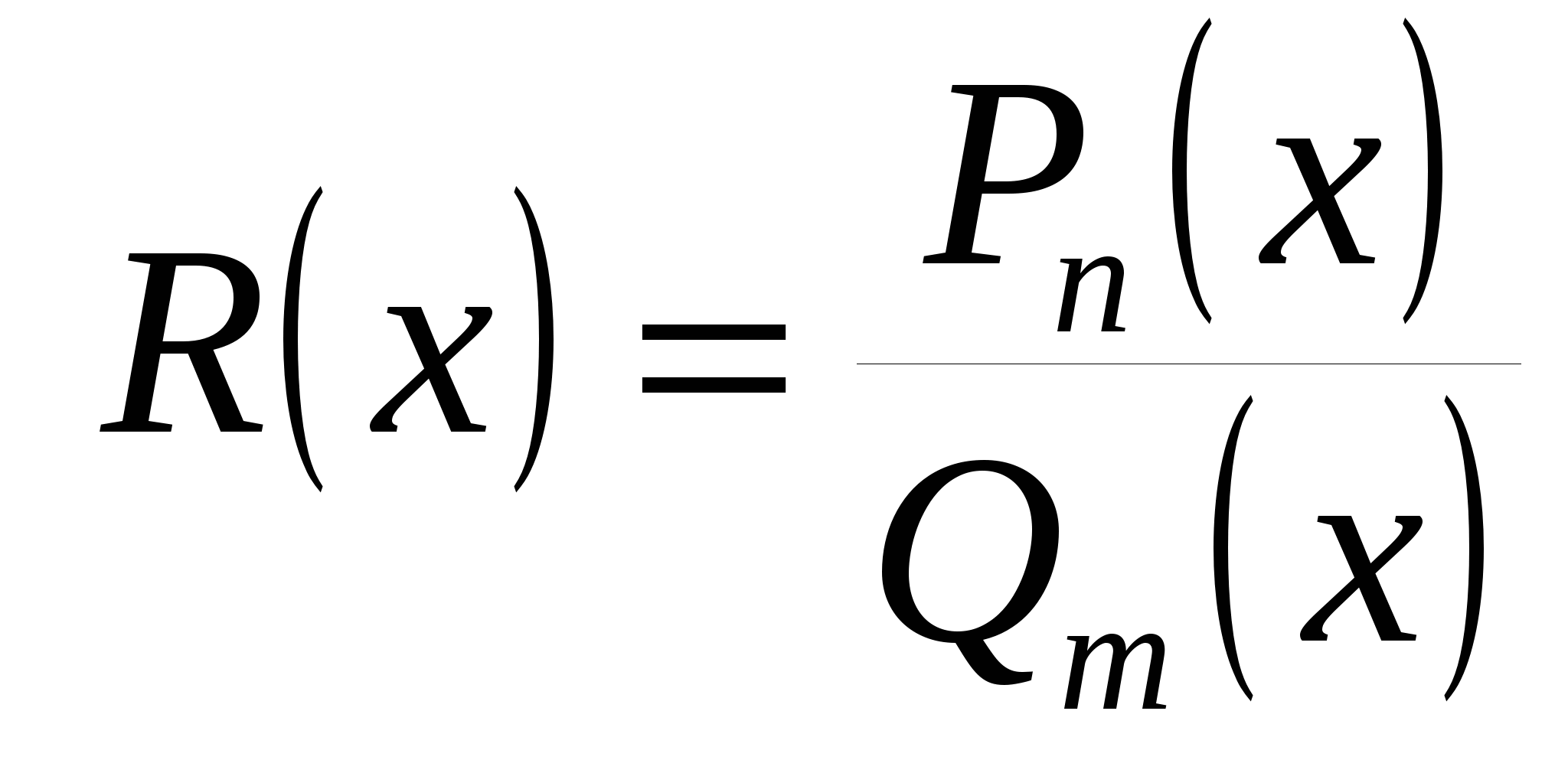 при при 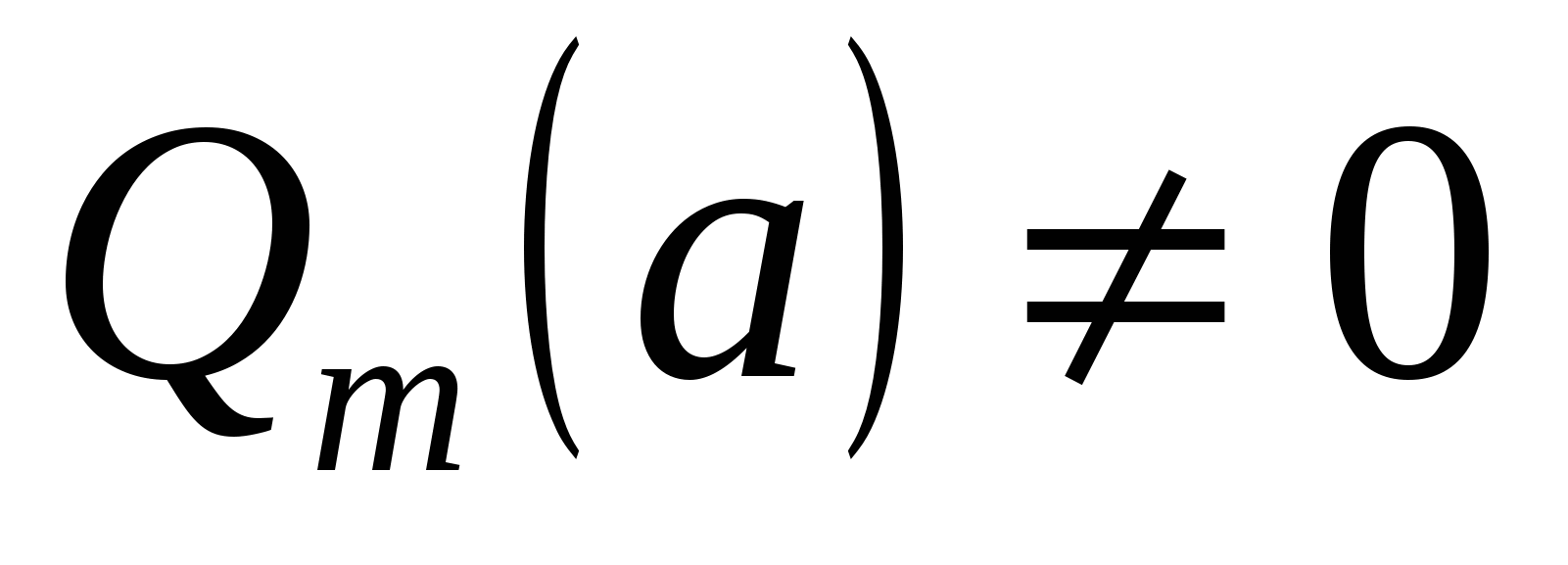 . .
3) Функция 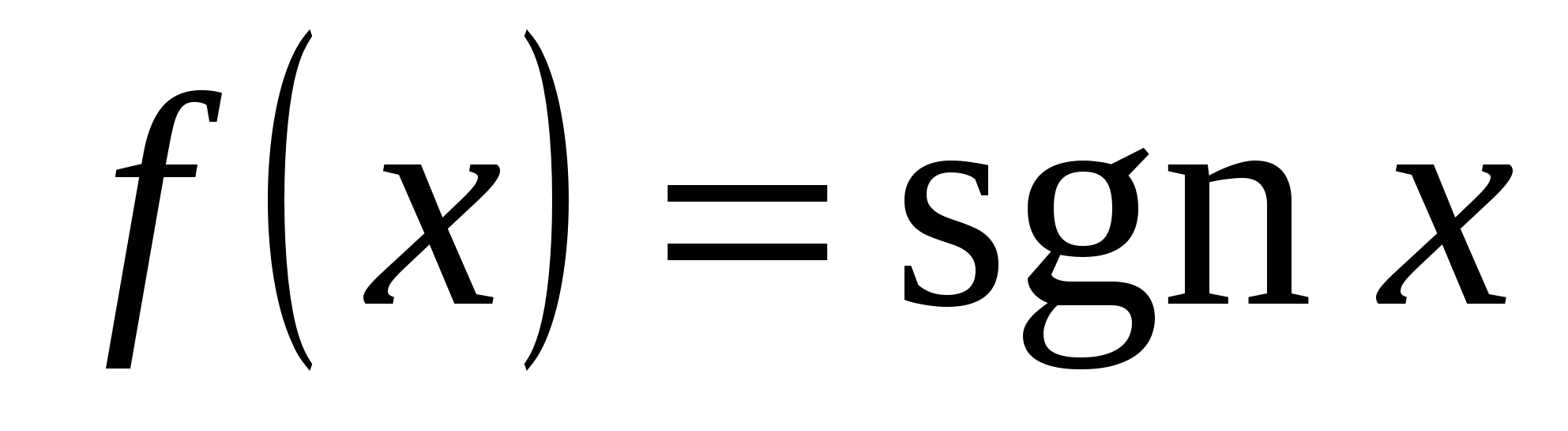 свойством непрерывности в точке свойством непрерывности в точке 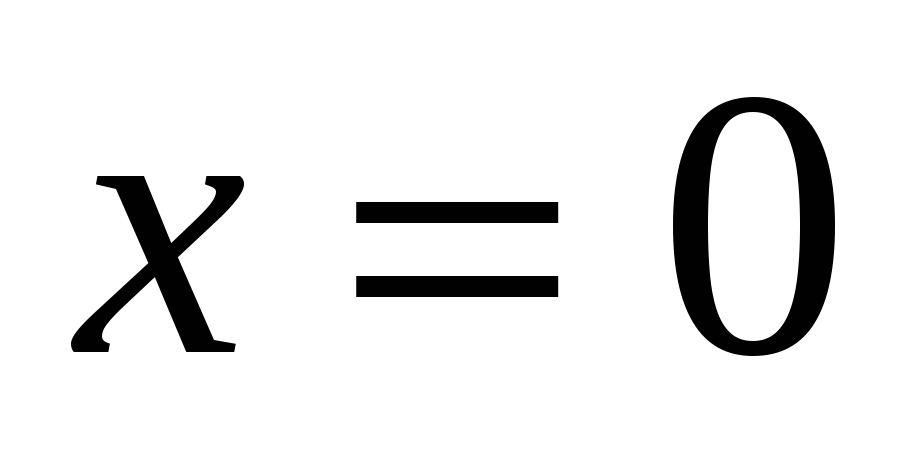 не обладает. не обладает.
Определение непрерывности в точке а может быть записано и так:
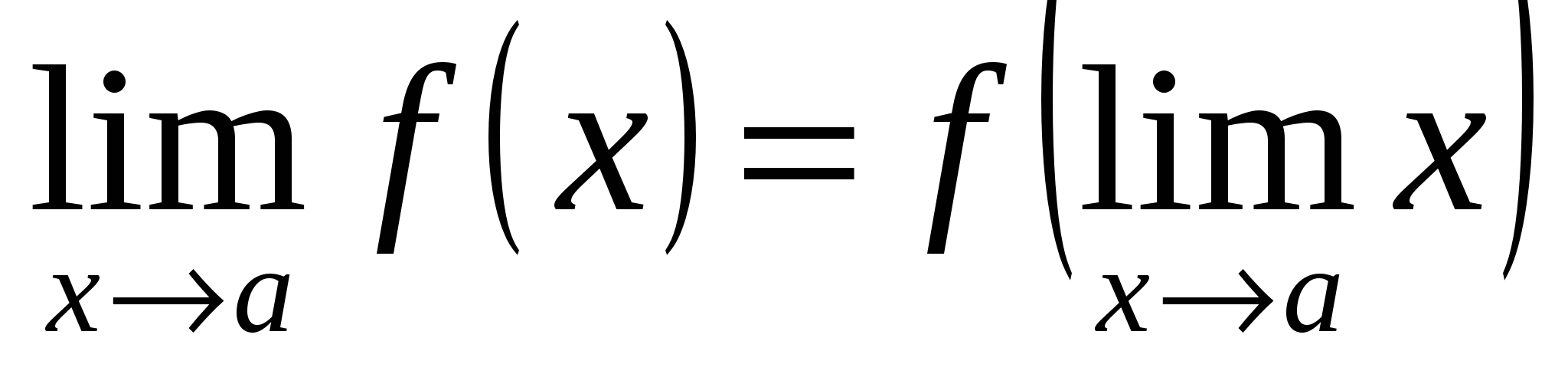 , ,
то есть для непрерывной функции возможна перестановка символов предела и функции. Очевидно, что непрерывность функции в данной точке выражается непрерывностью её графика при прохождении данной точки (без отрыва карандаша от листа бумаги).
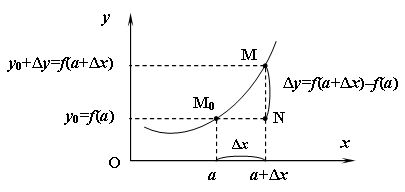
Дадим аргументу а приращение 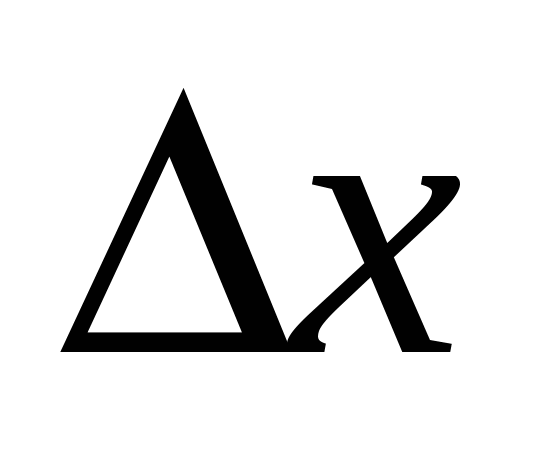 . Тогда функция . Тогда функция 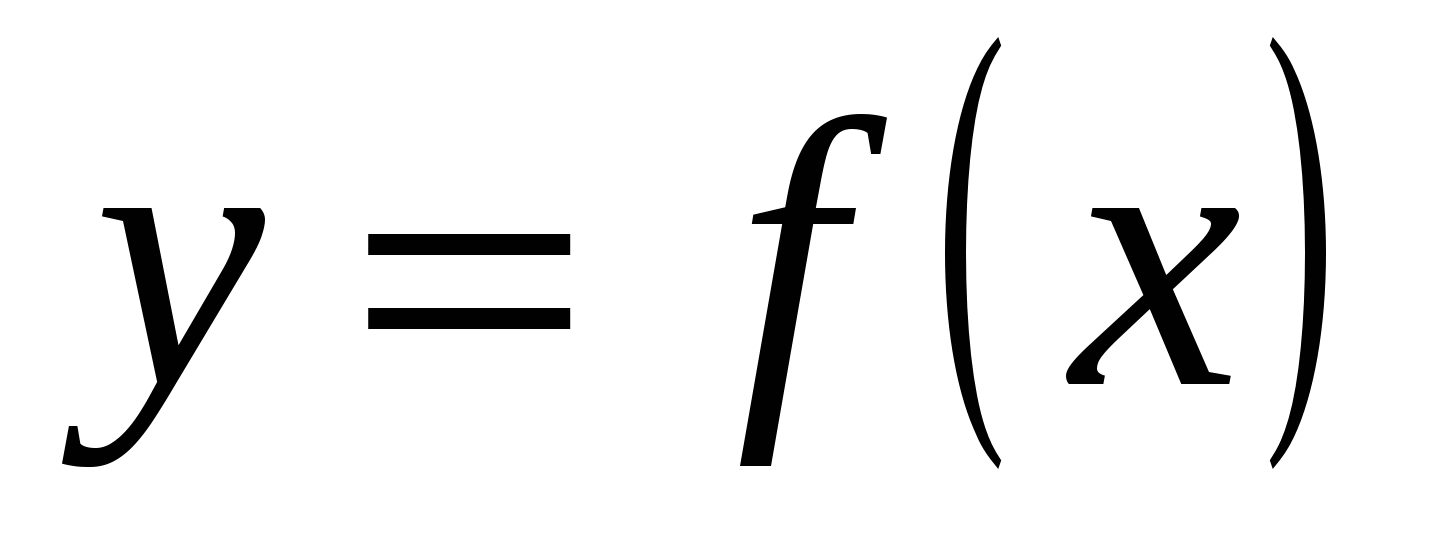 получит приращение получит приращение  , определяемое как разность наращенного и исходного значений функции (см. рис. 14.1): , определяемое как разность наращенного и исходного значений функции (см. рис. 14.1):
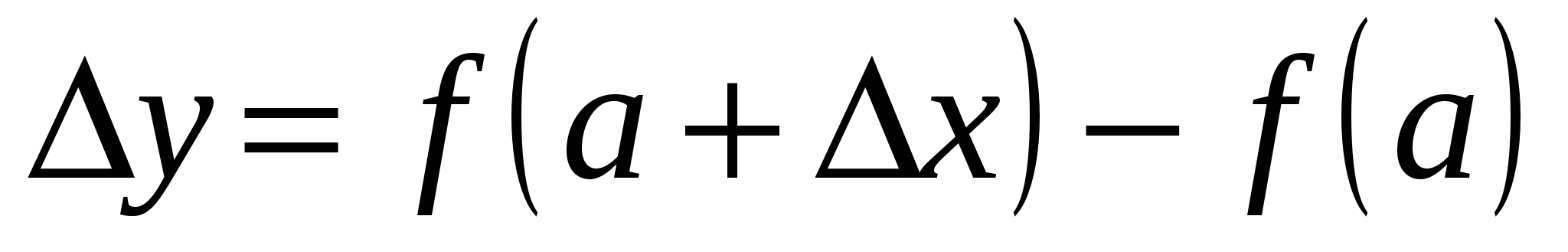 . .
Рис. 14.1.
|
|
Определение 14.3. Функция 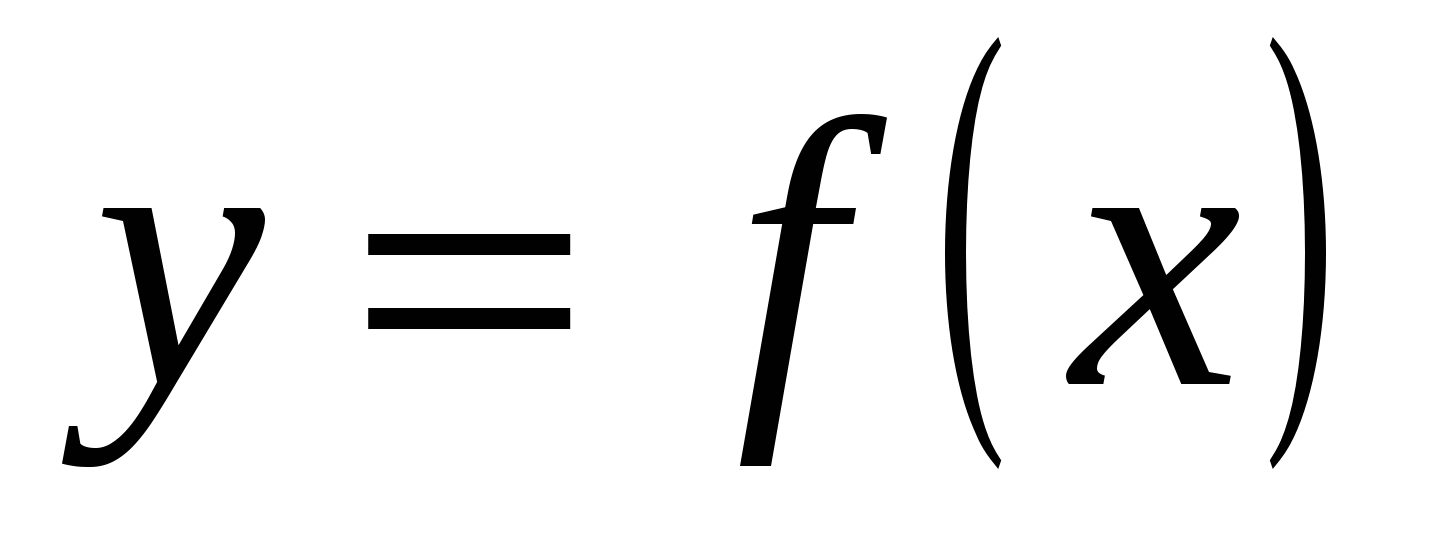 называется непрерывной в точке а, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: называется непрерывной в точке а, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 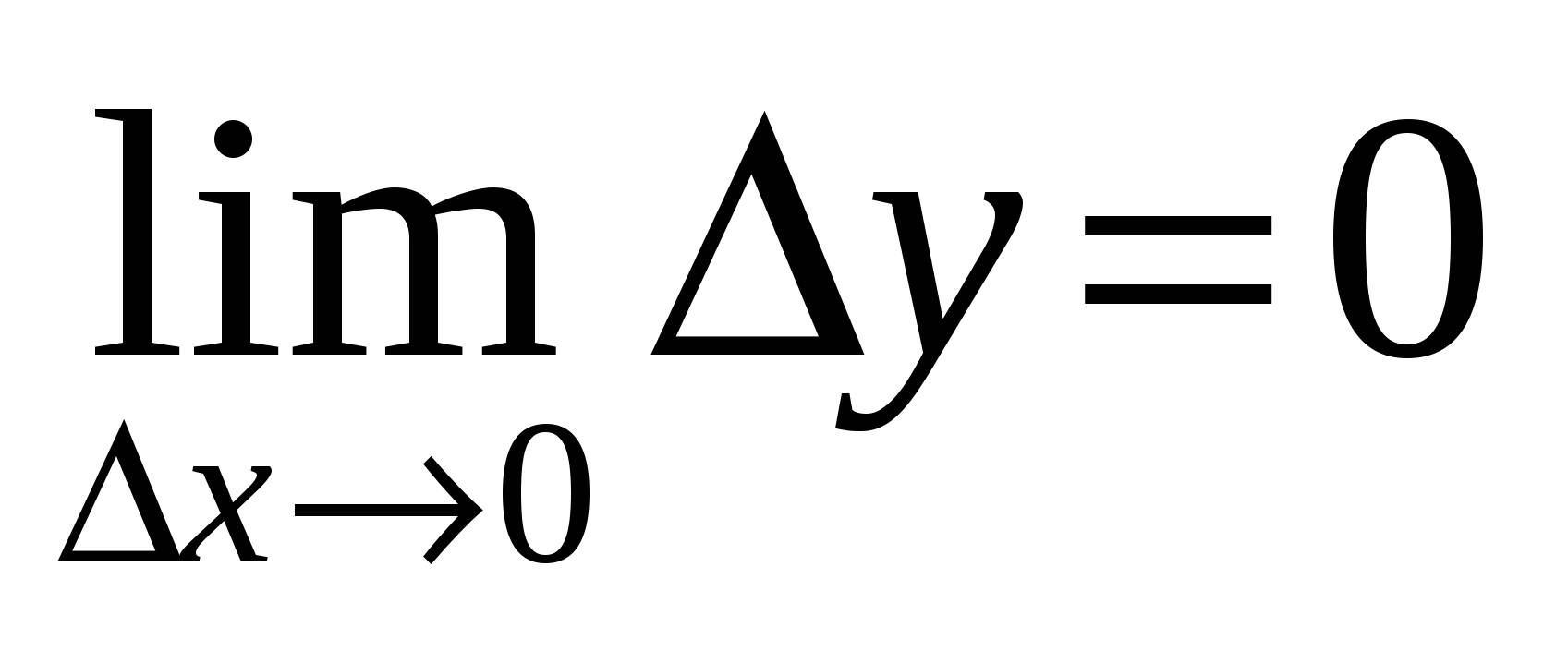 . .
Определение 14.4. Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва функции.
Например, функция Дирихле разрывна в каждой точке 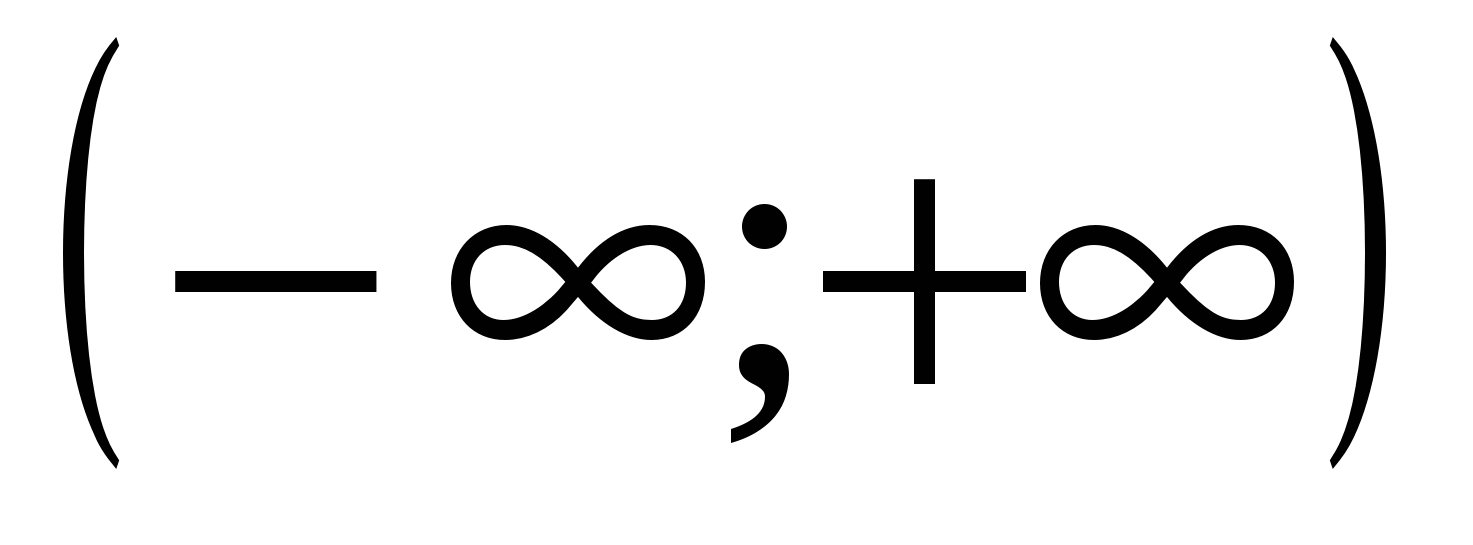 . .
Точки разрыва имеют различный характер и классифицируются следующим образом.
1) Если 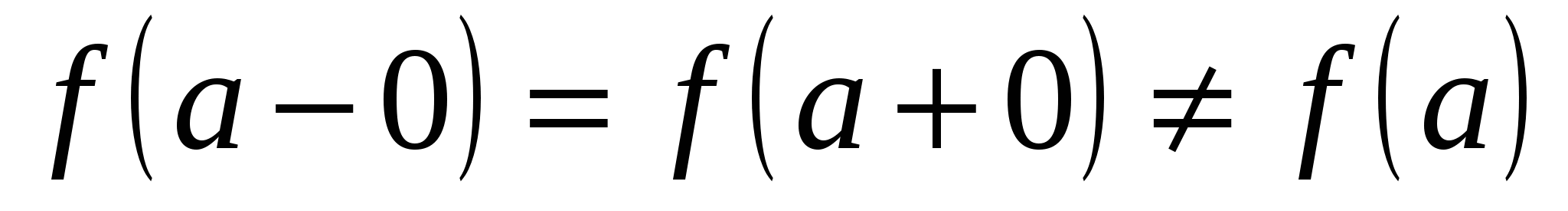 , то а называется точкой устранимого разрыва функции , то а называется точкой устранимого разрыва функции 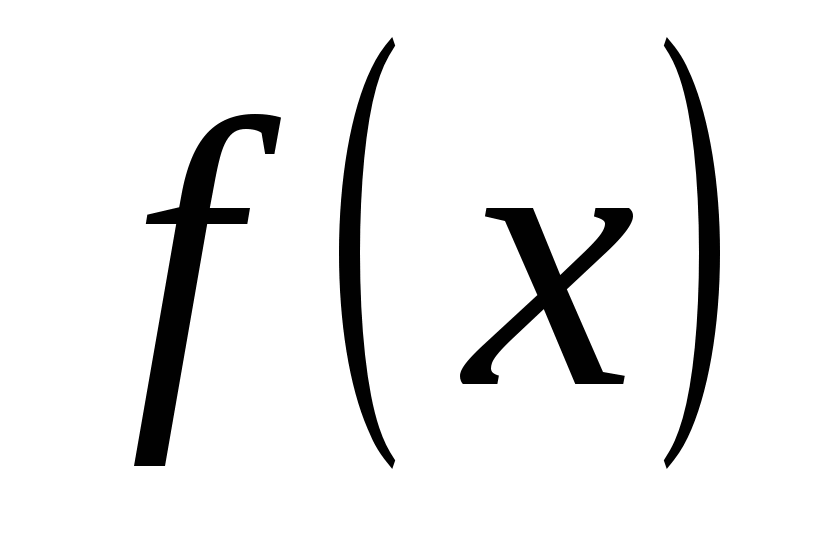 . При этом значение . При этом значение 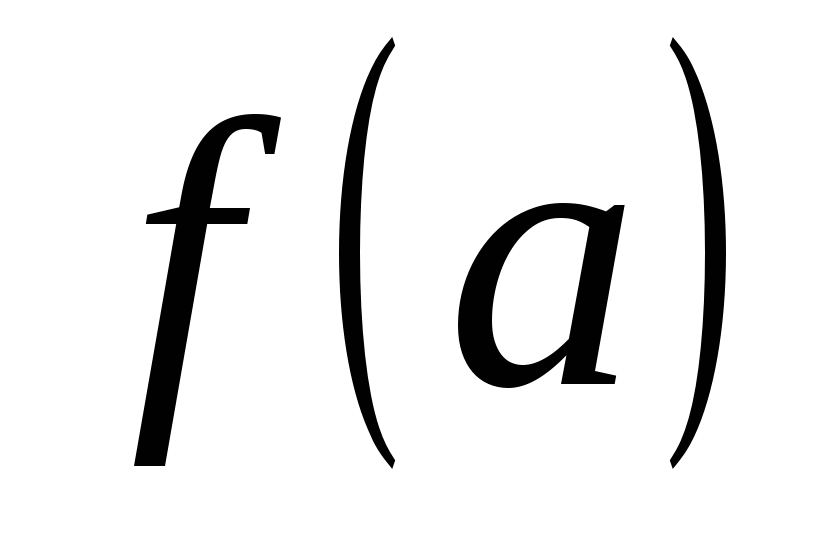 может быть и не определено. может быть и не определено.
2) Если 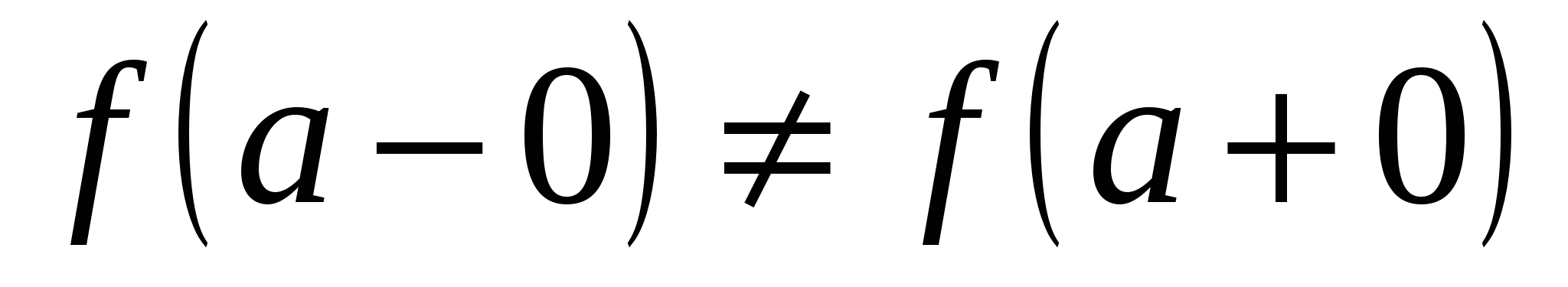 , то а называется точкой разрыва с конечным скачком функции , то а называется точкой разрыва с конечным скачком функции 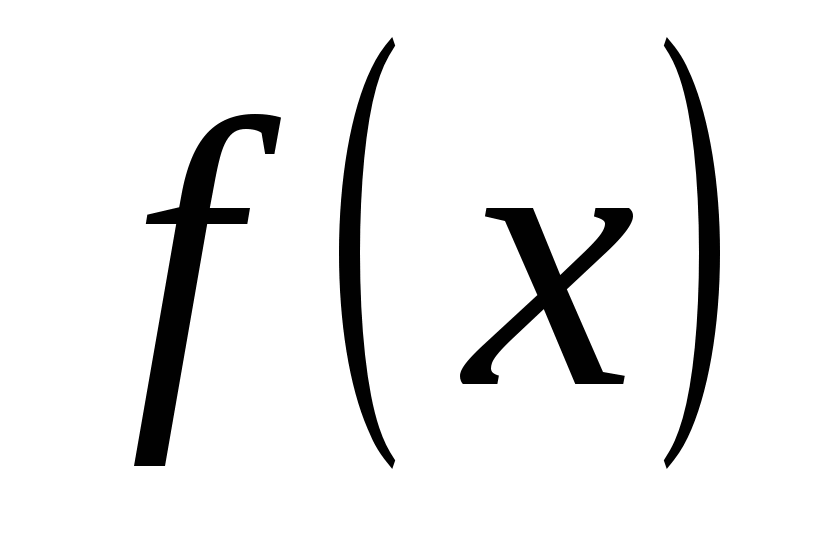 . Значение . Значение 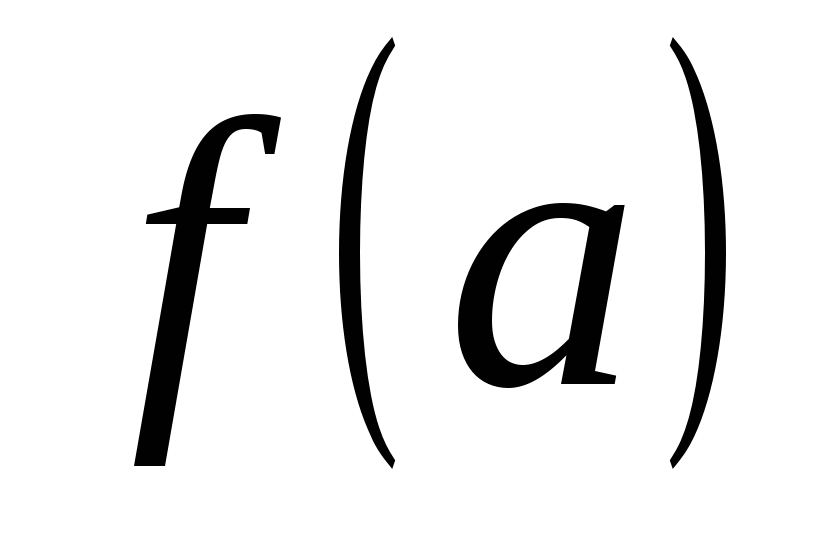 может быть любым, а может быть и не определено. может быть любым, а может быть и не определено.
3) Конечный скачок и устранимый разрыв функции 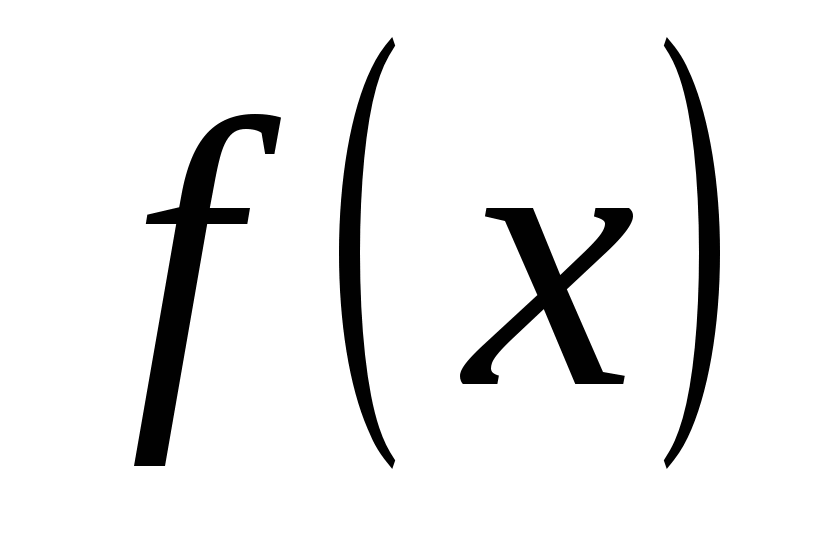 называются разрывами I рода. Их отличительным признаком является существование конечных односторонних пределов называются разрывами I рода. Их отличительным признаком является существование конечных односторонних пределов 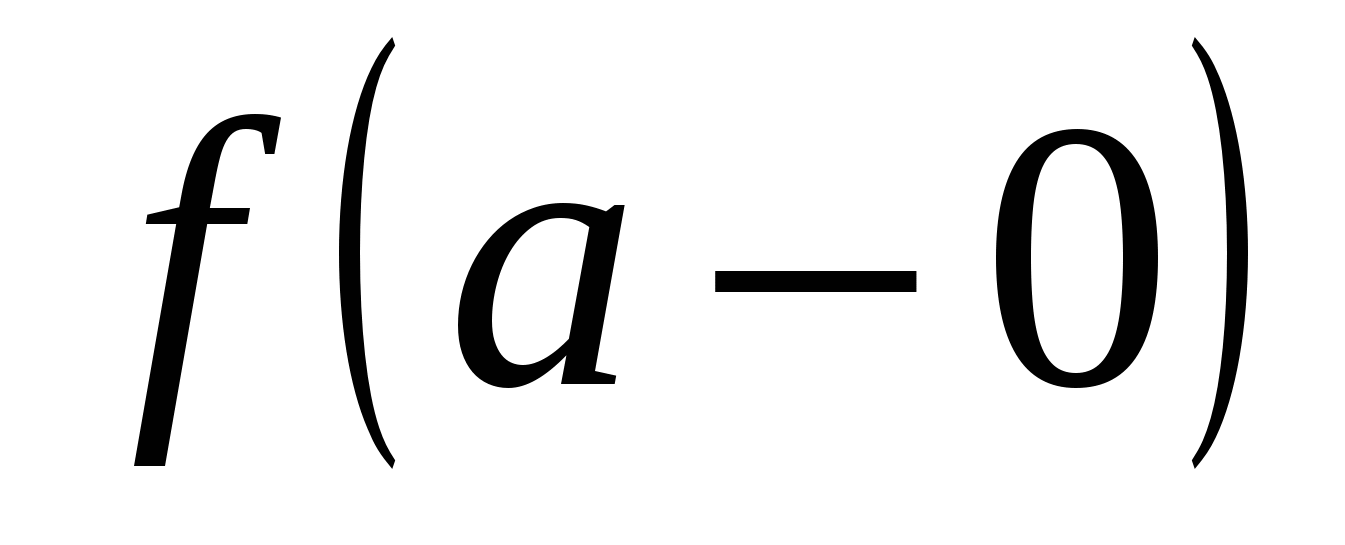 и и 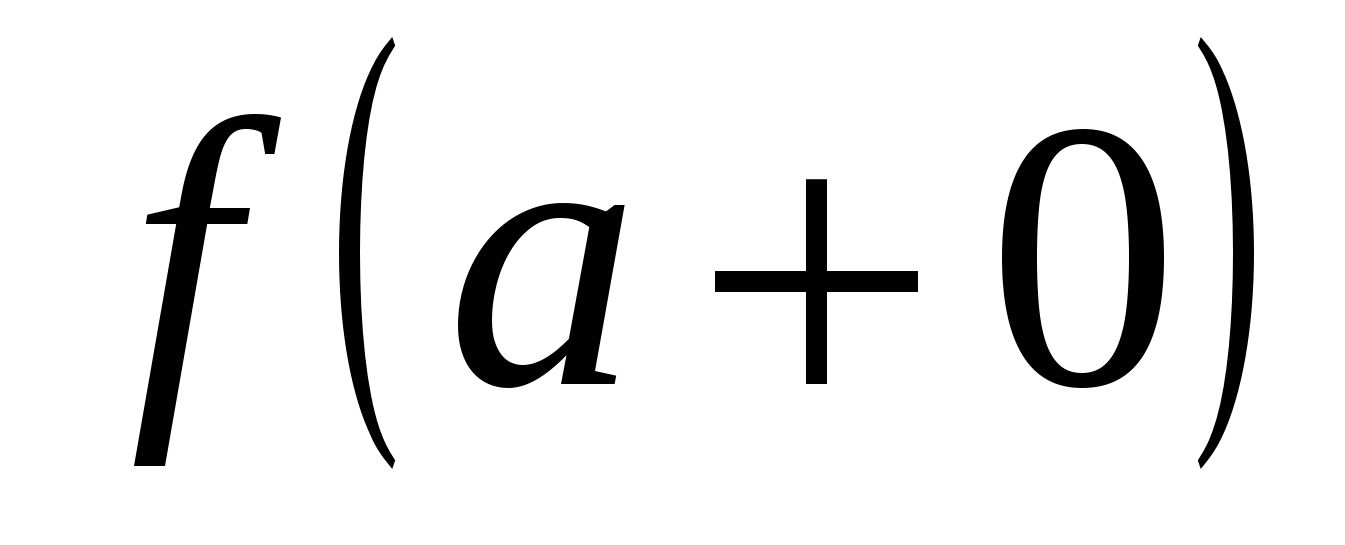 . .
Все другие разрывы называются разрывами II рода. В точке разрыва II рода хотя бы один из односторонних пределов равен бесконечности или не существует.
Пример 14.2. 1) Пусть 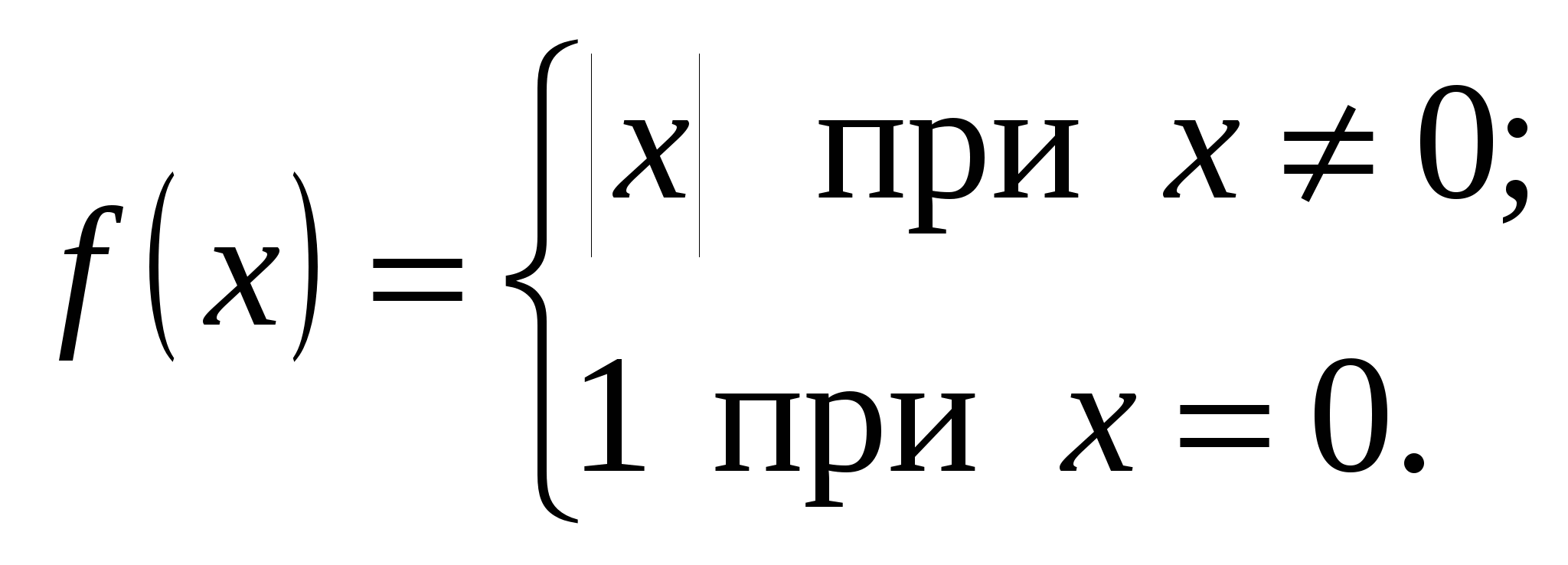 Очевидно, Очевидно, 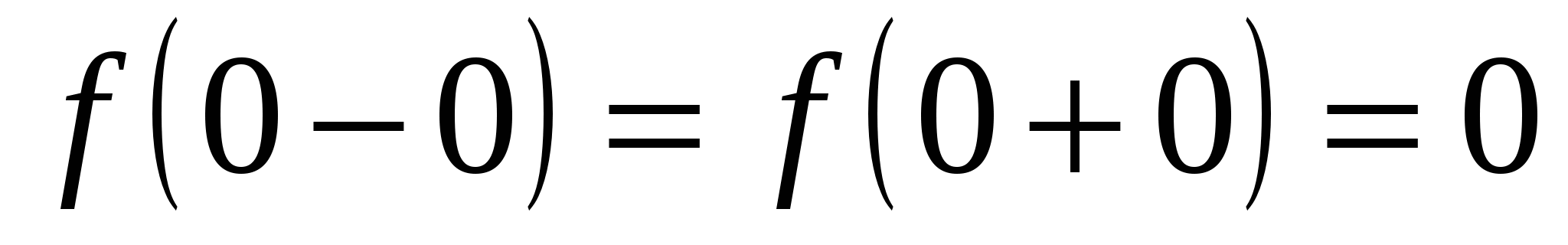 , но , но 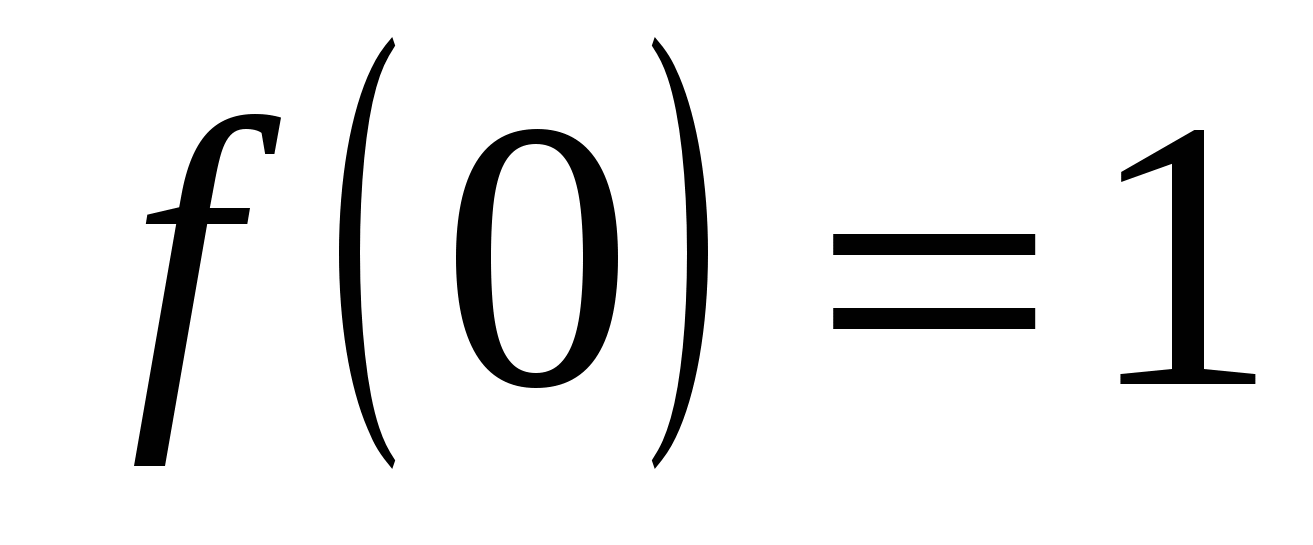 (рис. 14.2). Следовательно, (рис. 14.2). Следовательно, 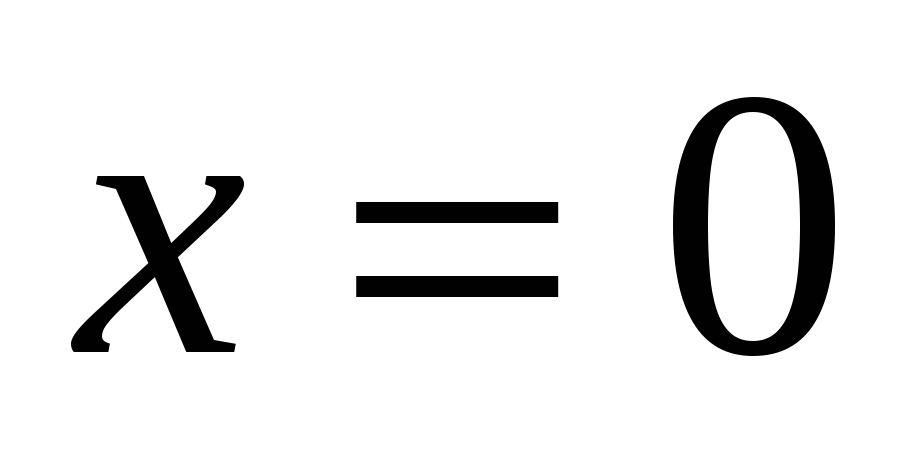 – точка устранимого разрыва функции – точка устранимого разрыва функции 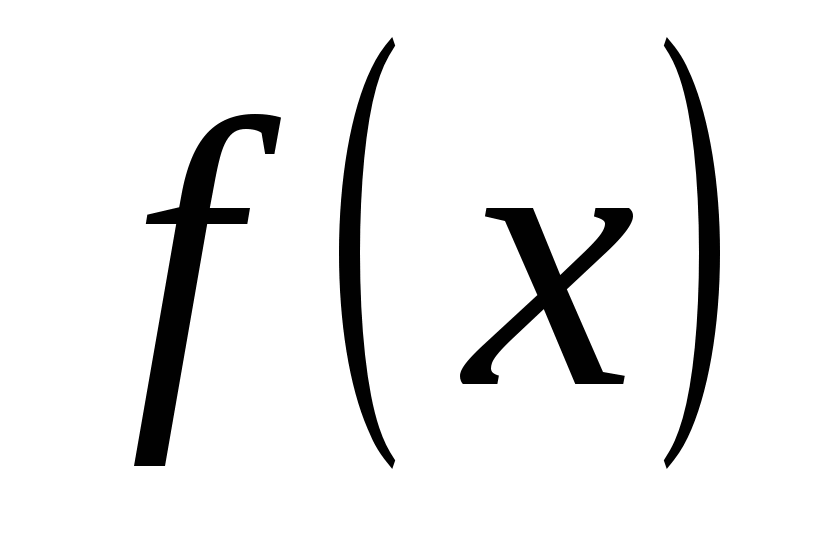 . Если положить . Если положить 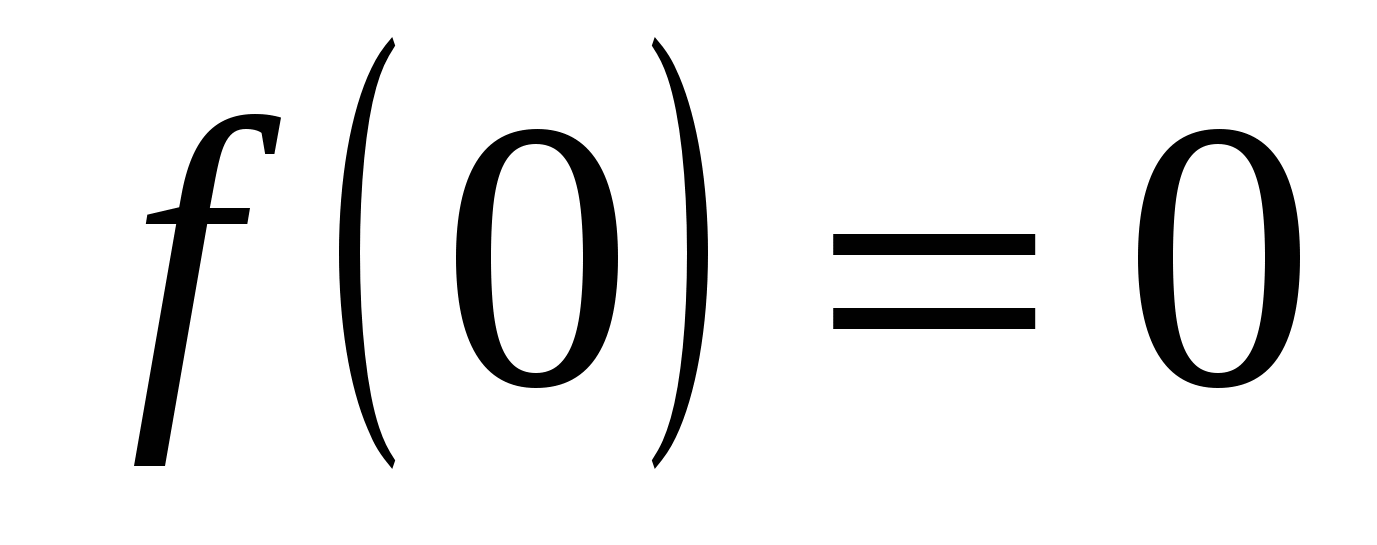 , то разрыв устраняется. , то разрыв устраняется.
|
Рис. 14.2.
|
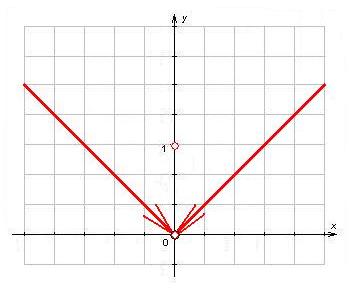
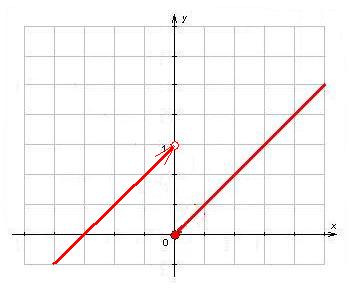
2) Пусть 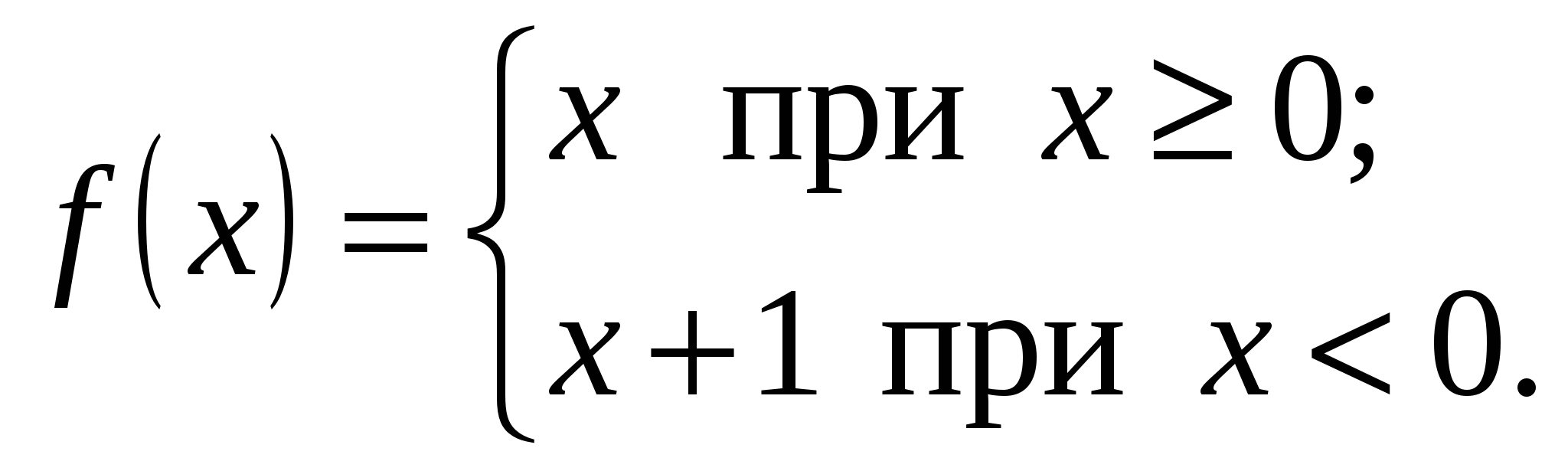 Здесь Здесь 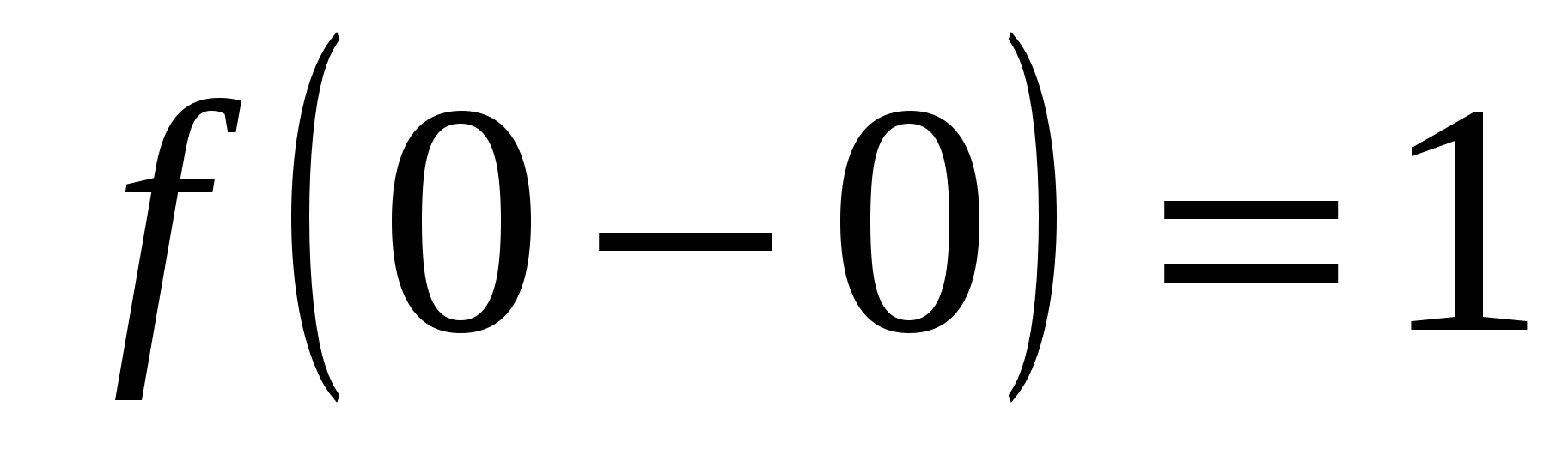 , , 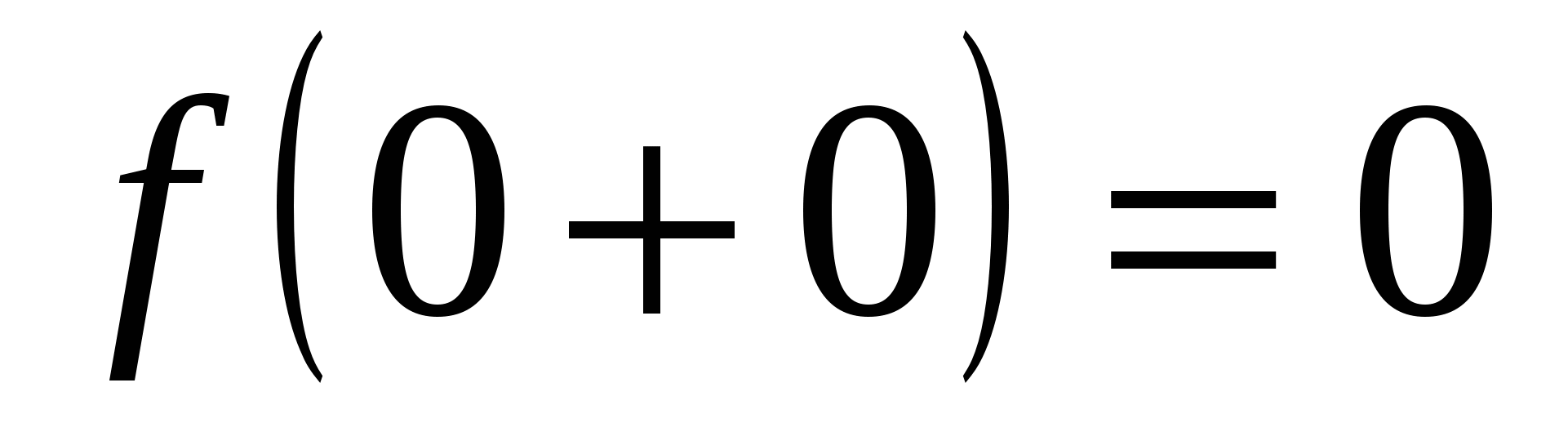 (рис. 14.3). Следовательно, (рис. 14.3). Следовательно, 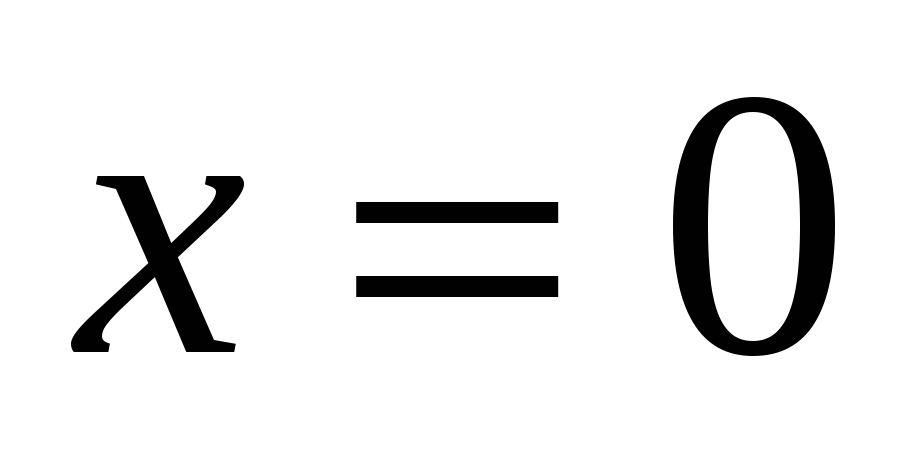 – точка разрыва с конечным скачком функции – точка разрыва с конечным скачком функции 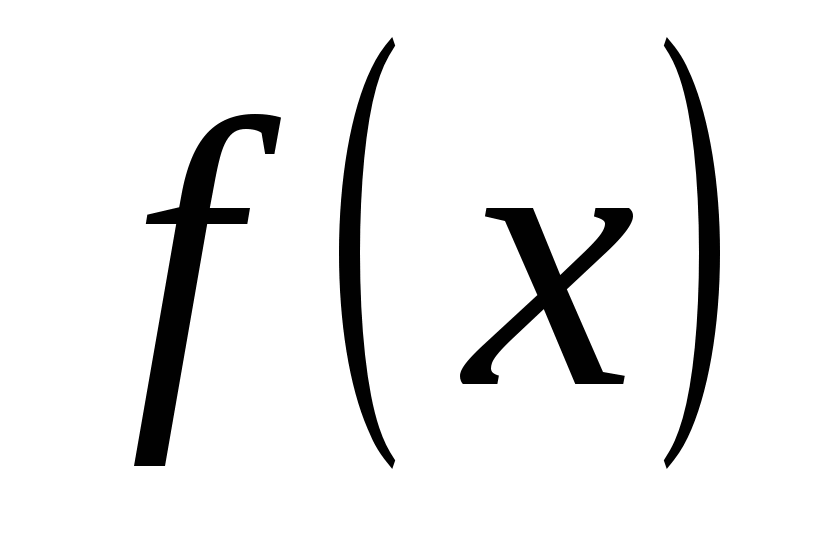 . При переходе через точку . При переходе через точку 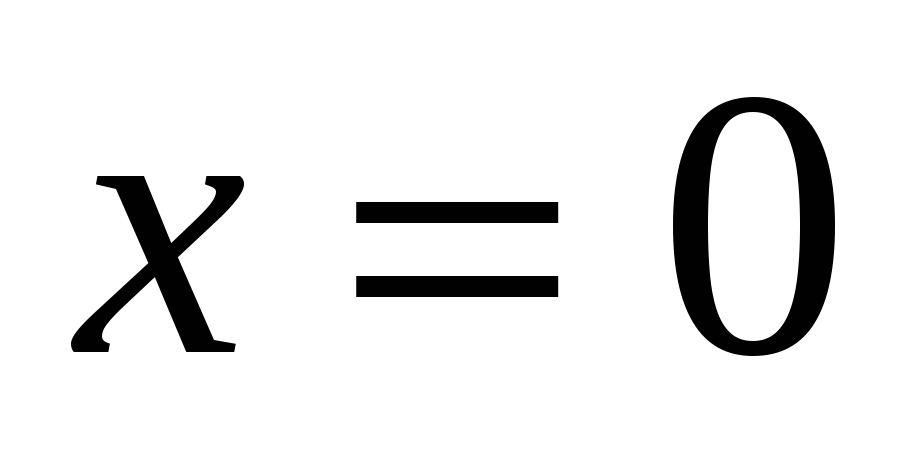 значения функции значения функции 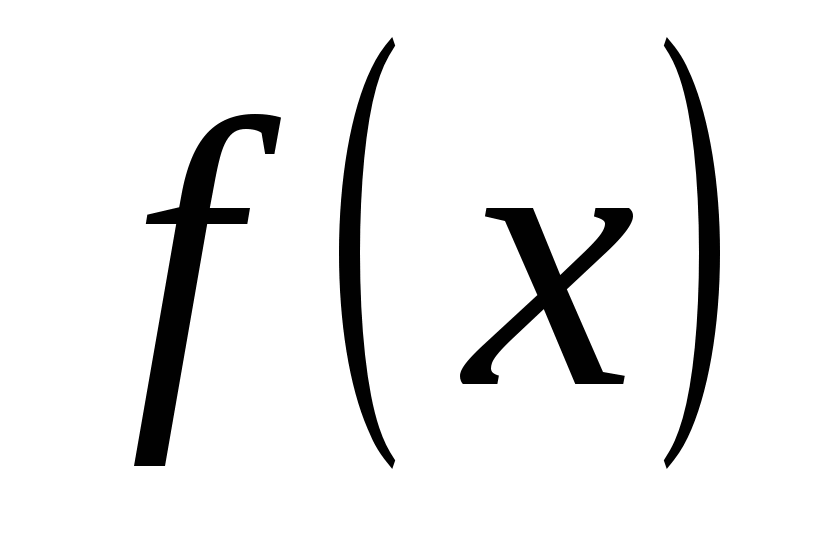 меняются скачком от значений, сколь угодно близких к 1 при меняются скачком от значений, сколь угодно близких к 1 при 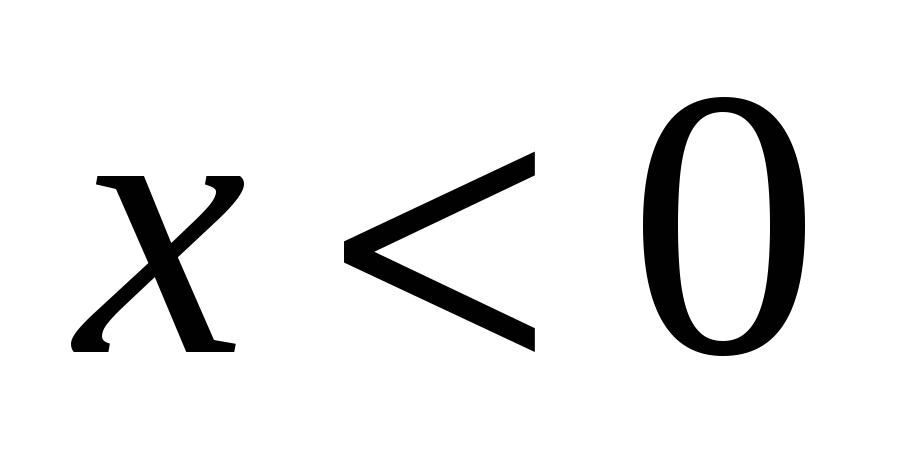 к значению, равному 0 в точке к значению, равному 0 в точке 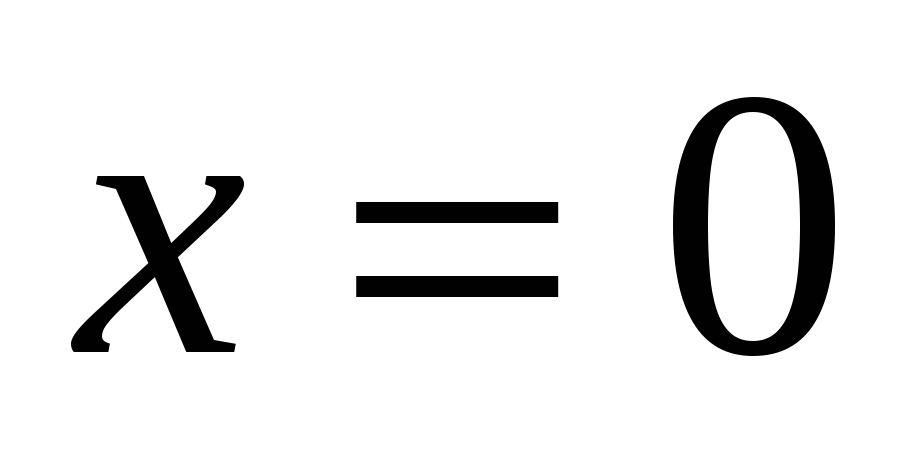 , и значениям, сколь угодно близким к 0 при , и значениям, сколь угодно близким к 0 при 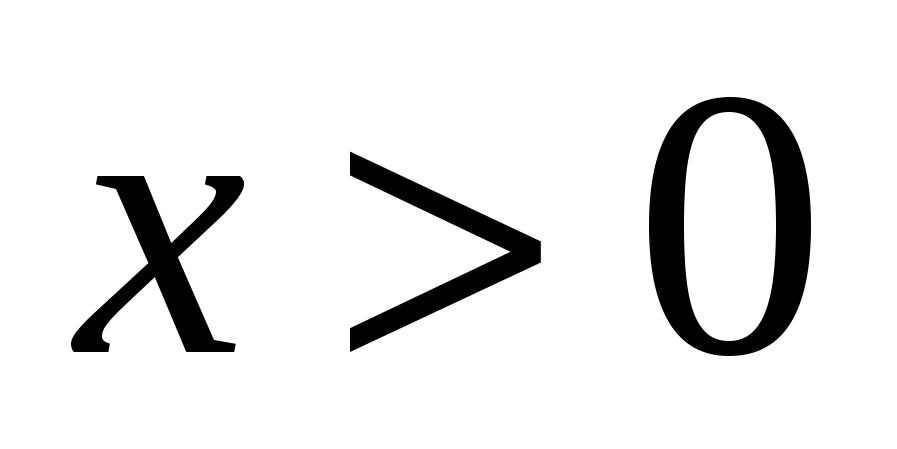 . .
|
Рис. 14.3.
|
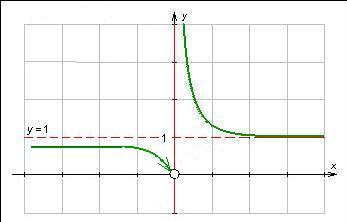
3) Пусть 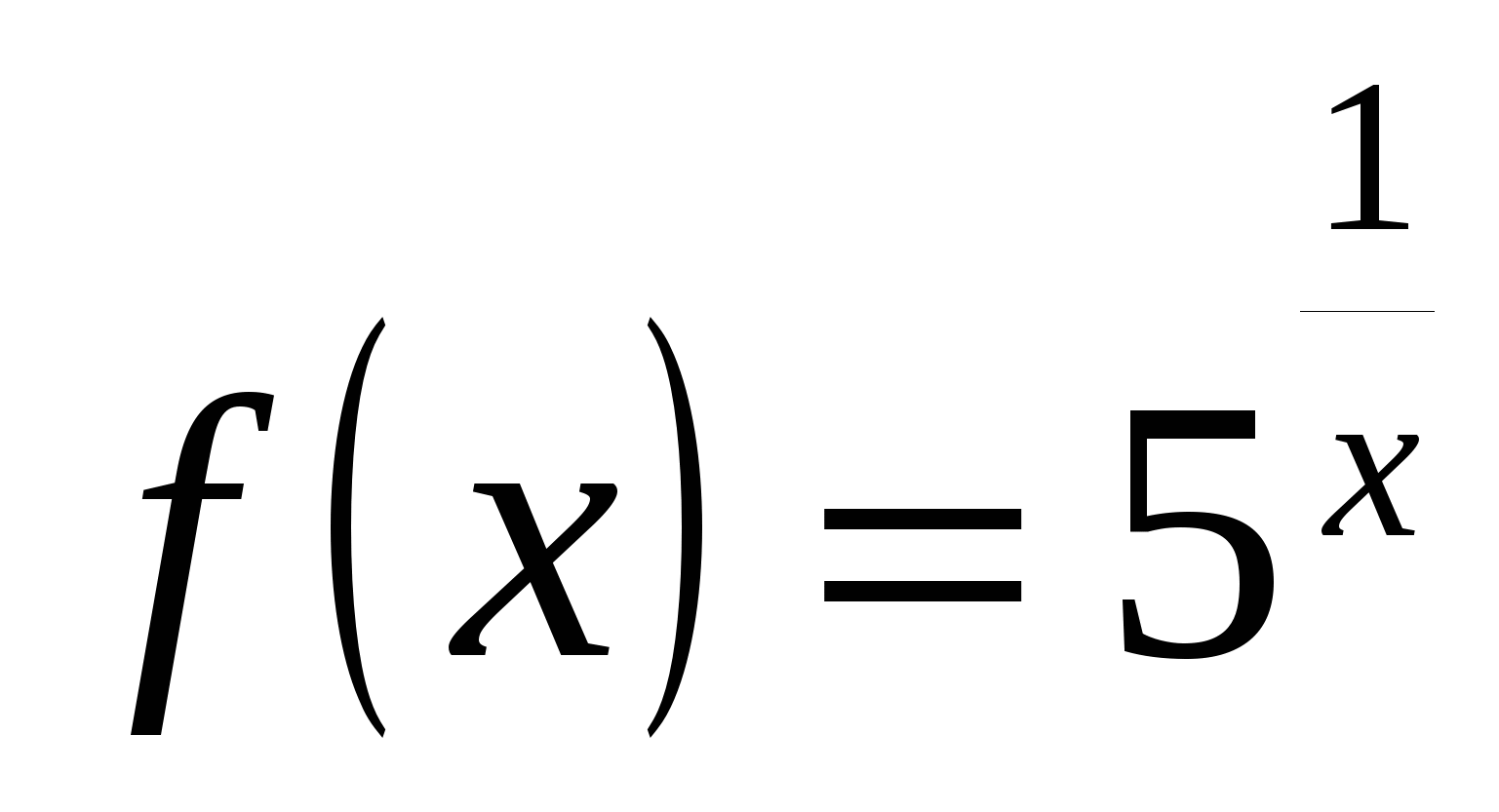 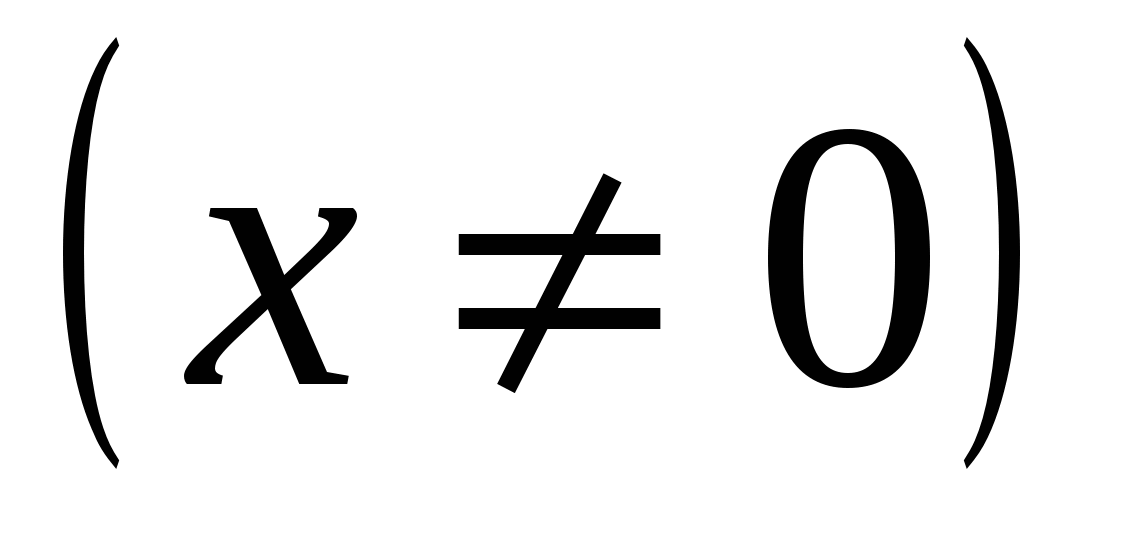 . Определим односторонние пределы: . Определим односторонние пределы: 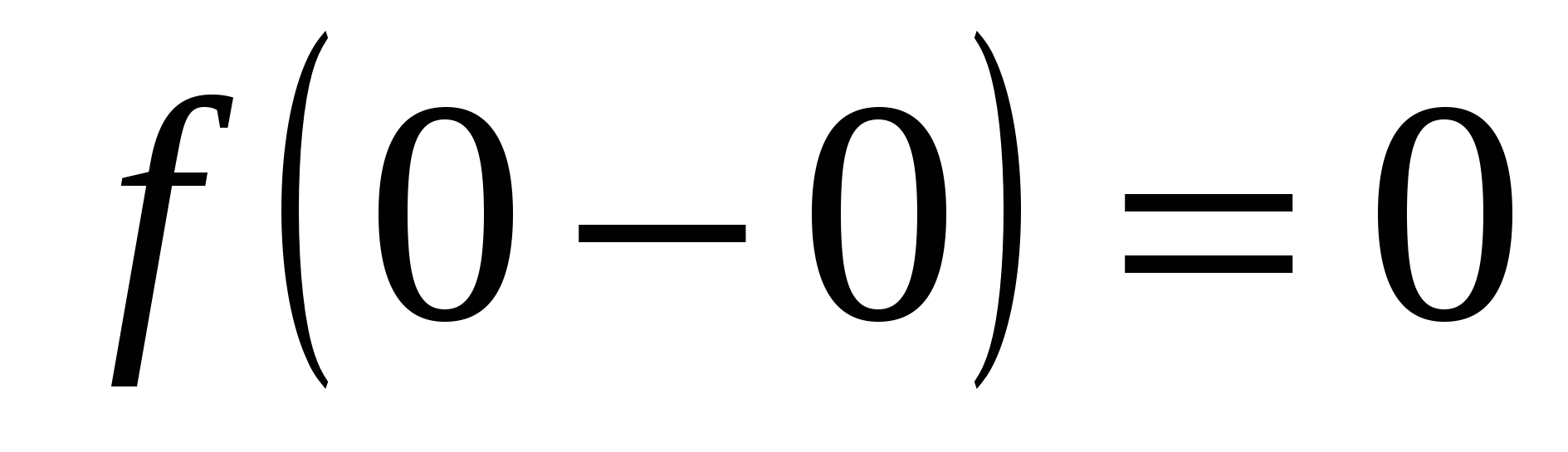 , , 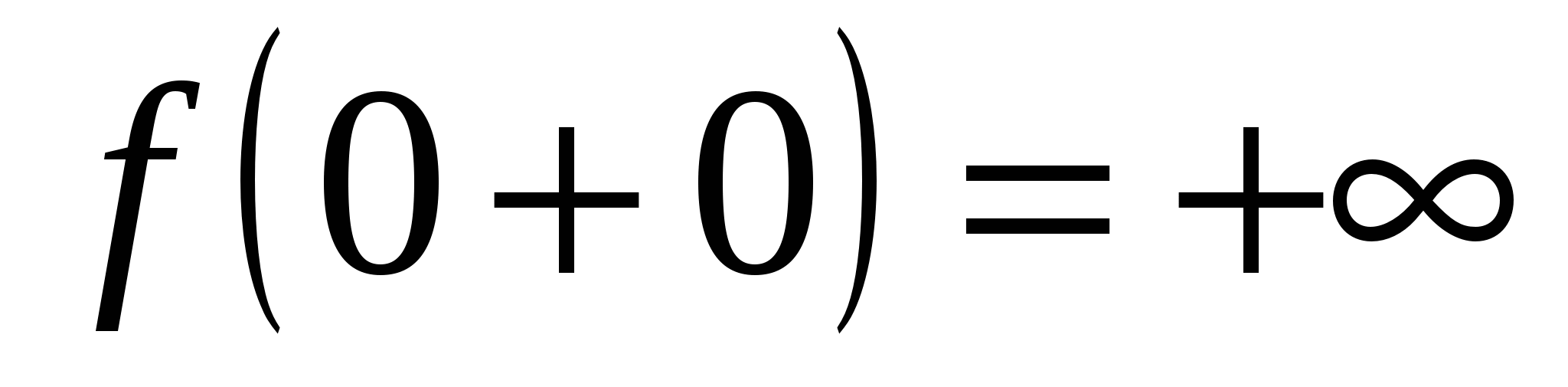 . Точка . Точка 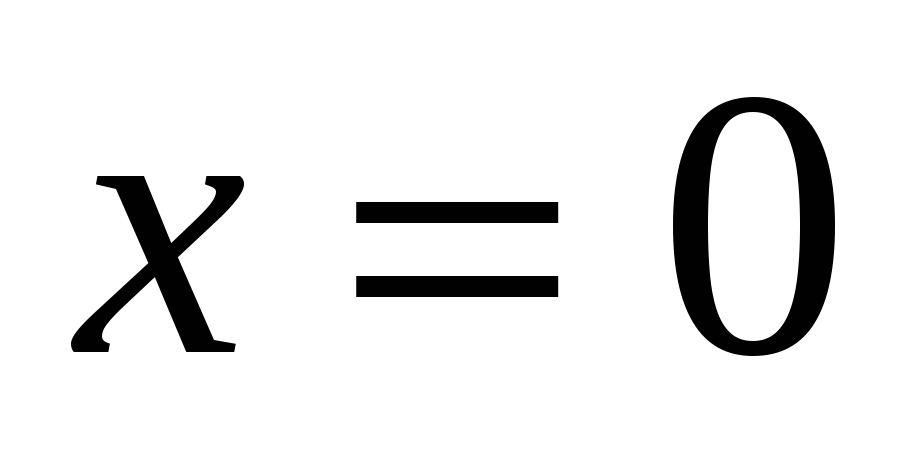 – точка разрыва функции – точка разрыва функции 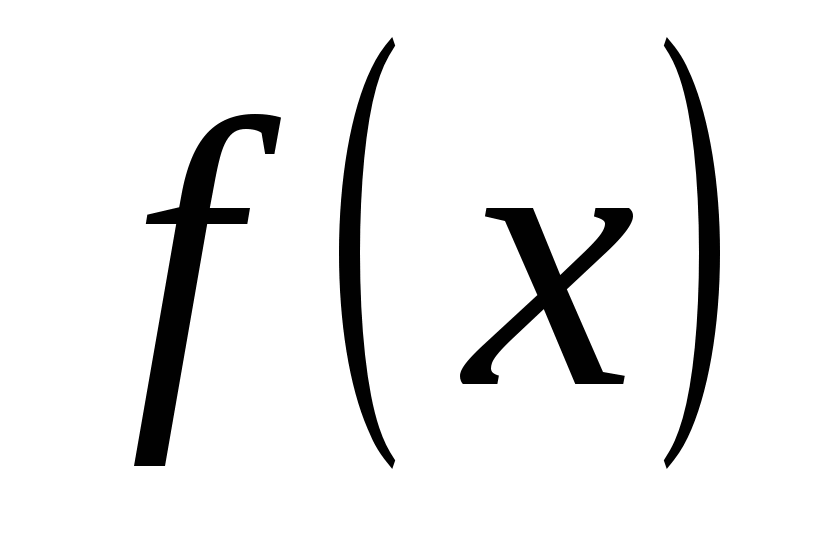 II рода (рис. 14.4). II рода (рис. 14.4).
|
Рис. 14.4.
|
Определение 14.5. Функция непрерывна на множестве 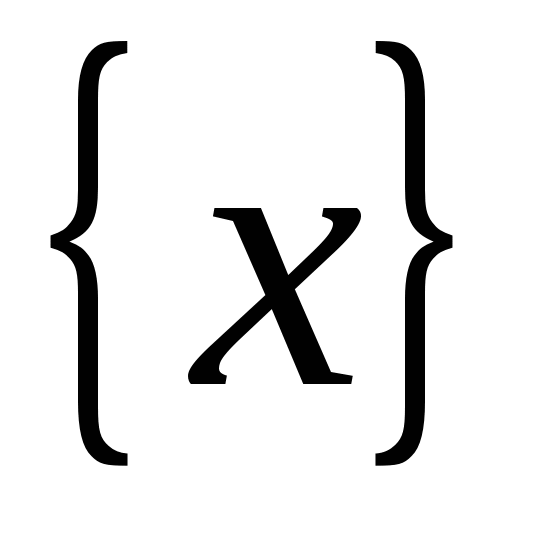 , если она непрерывна в любой точке , если она непрерывна в любой точке 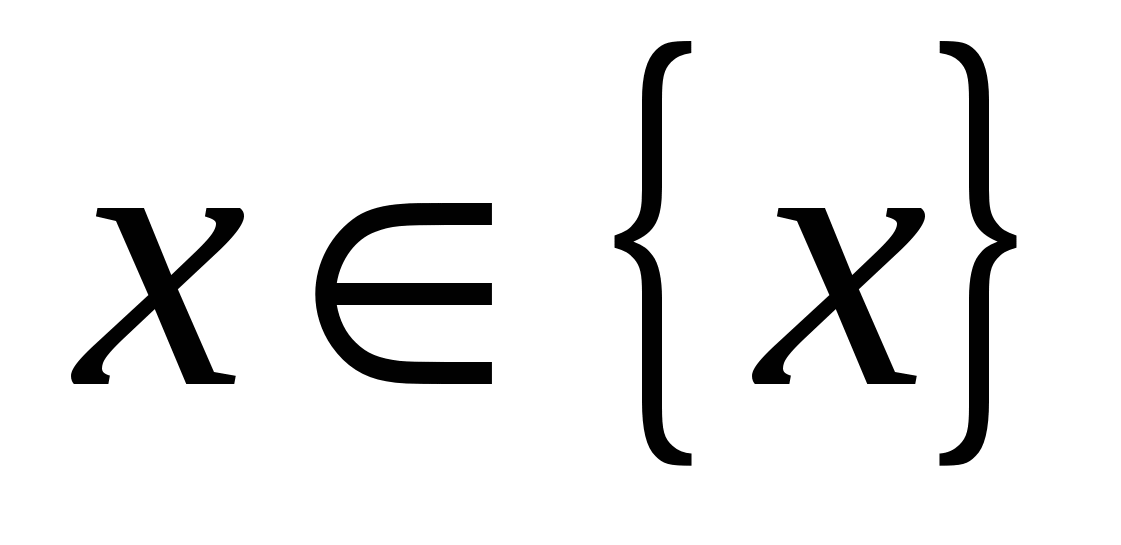 . Функция непрерывна на интервале . Функция непрерывна на интервале 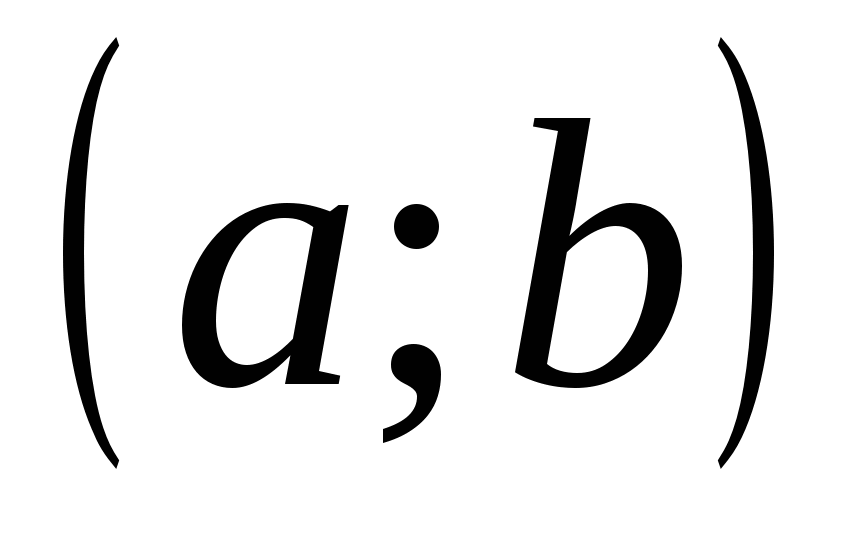 или на сегменте или на сегменте 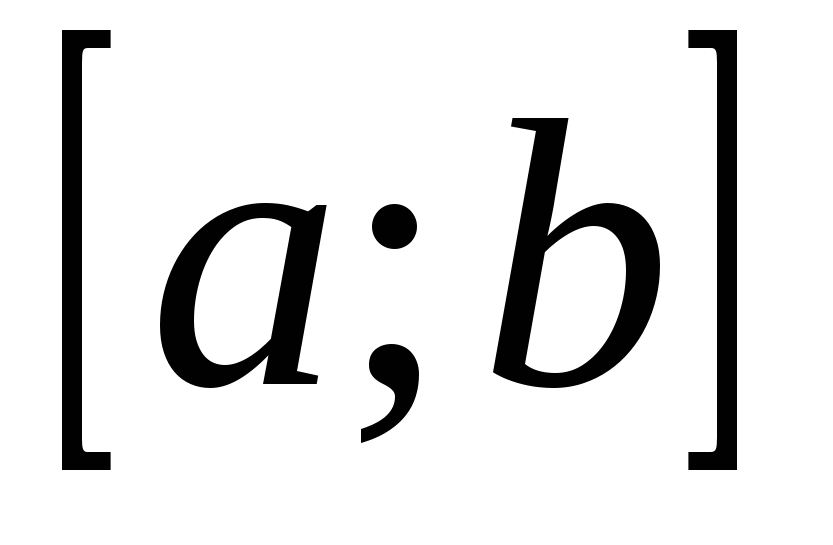 , если , если
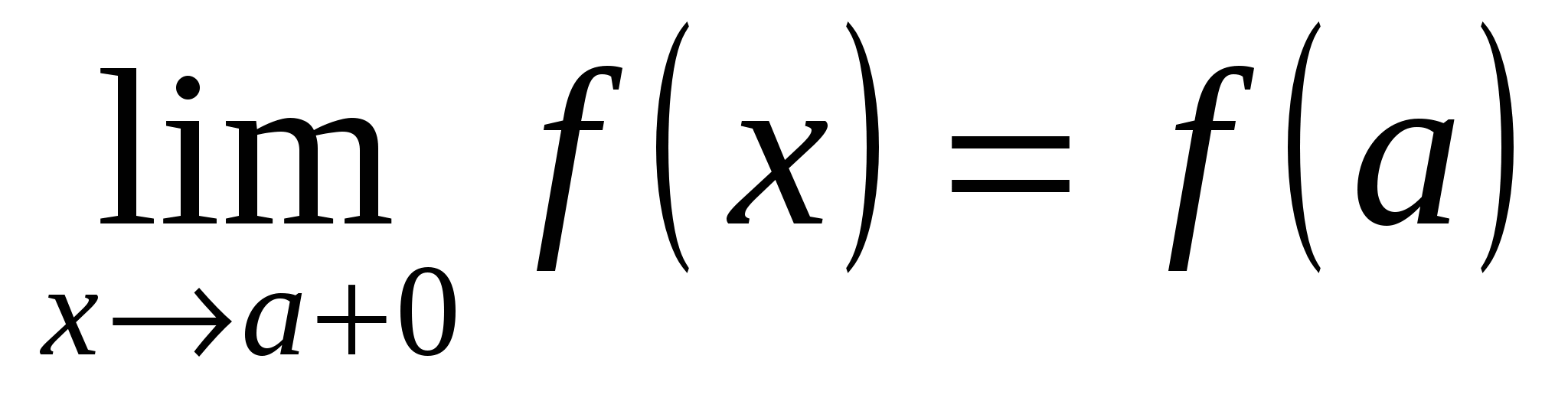 ; ; 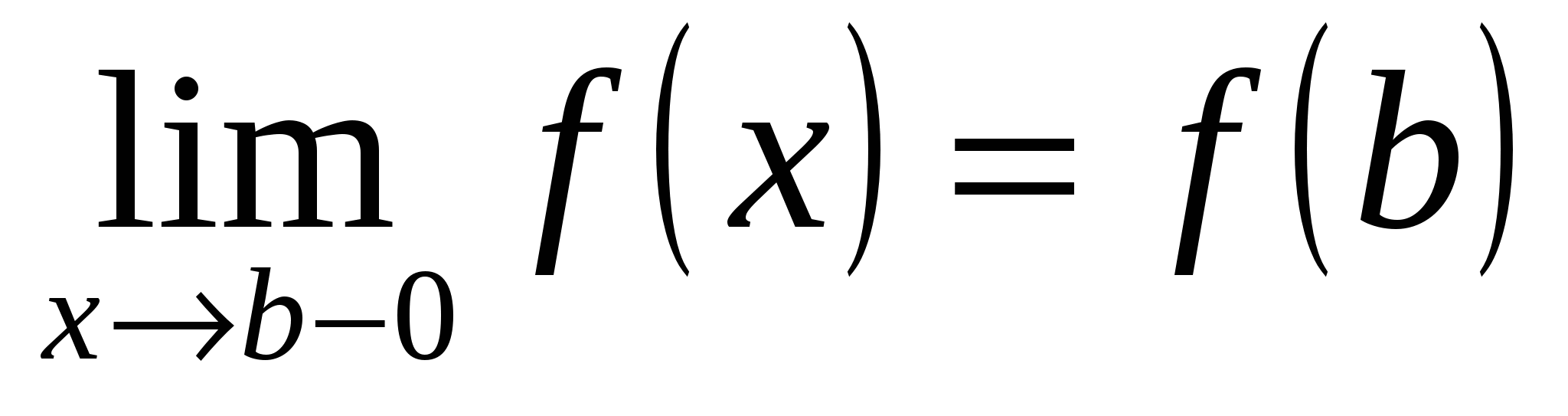 . .
14.2. Свойства функций, непрерывных в точке.
♦ Теорема 14.1. 1) Если функции 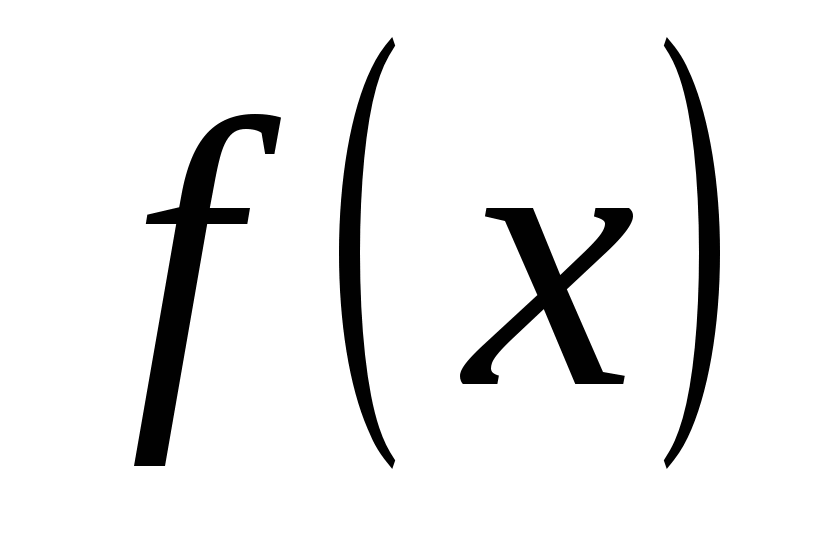 и и 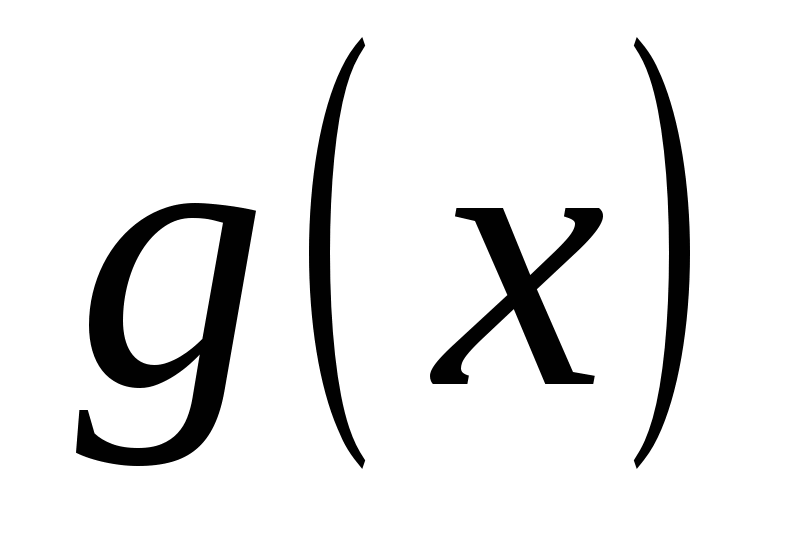 определены на определены на 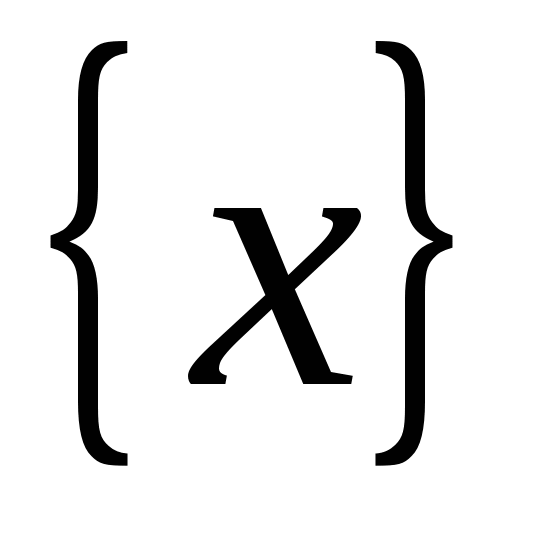 и непрерывны в точке a, то их алгебраическая сумма (разность) и непрерывны в точке a, то их алгебраическая сумма (разность) 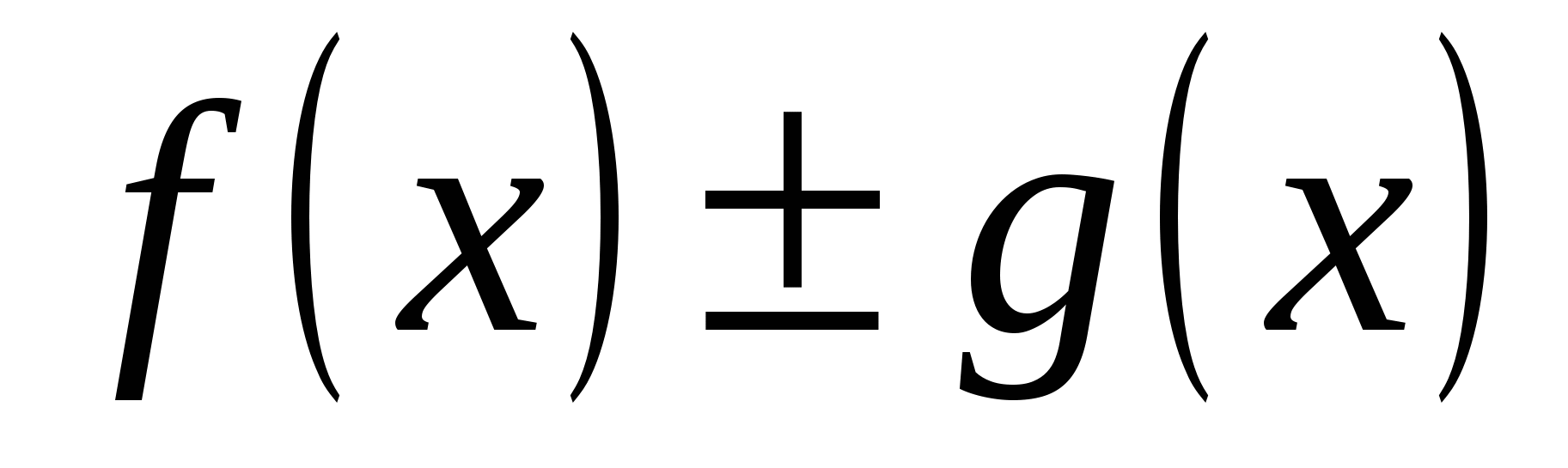 , произведение , произведение 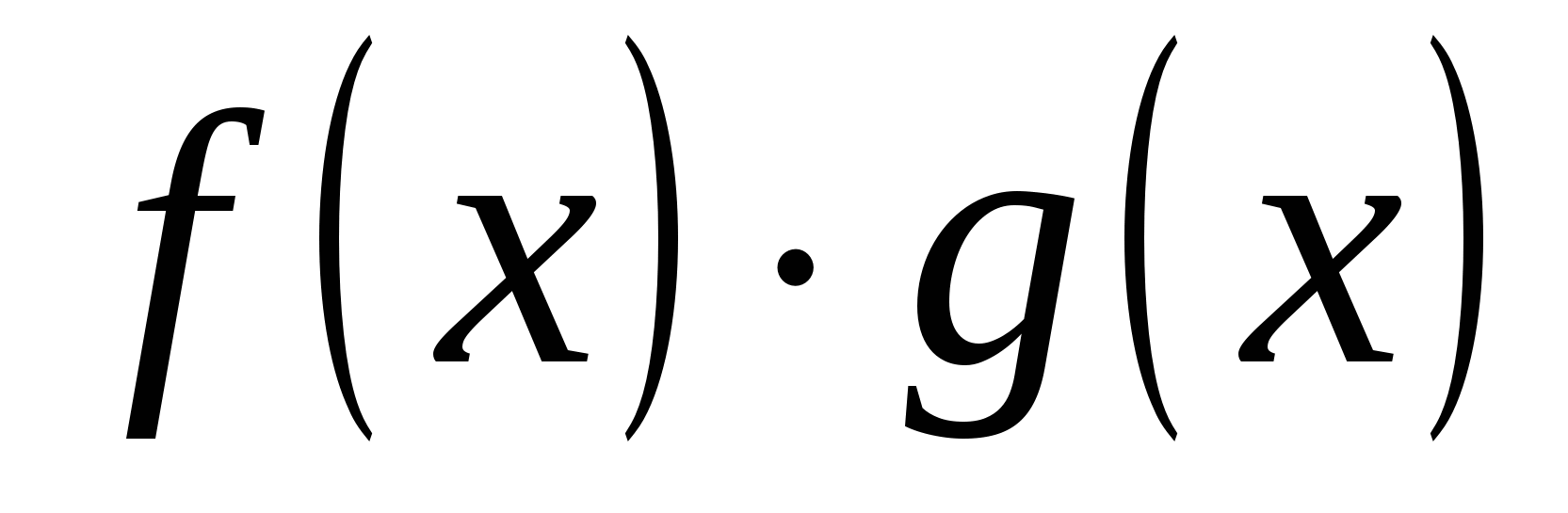 и частное и частное 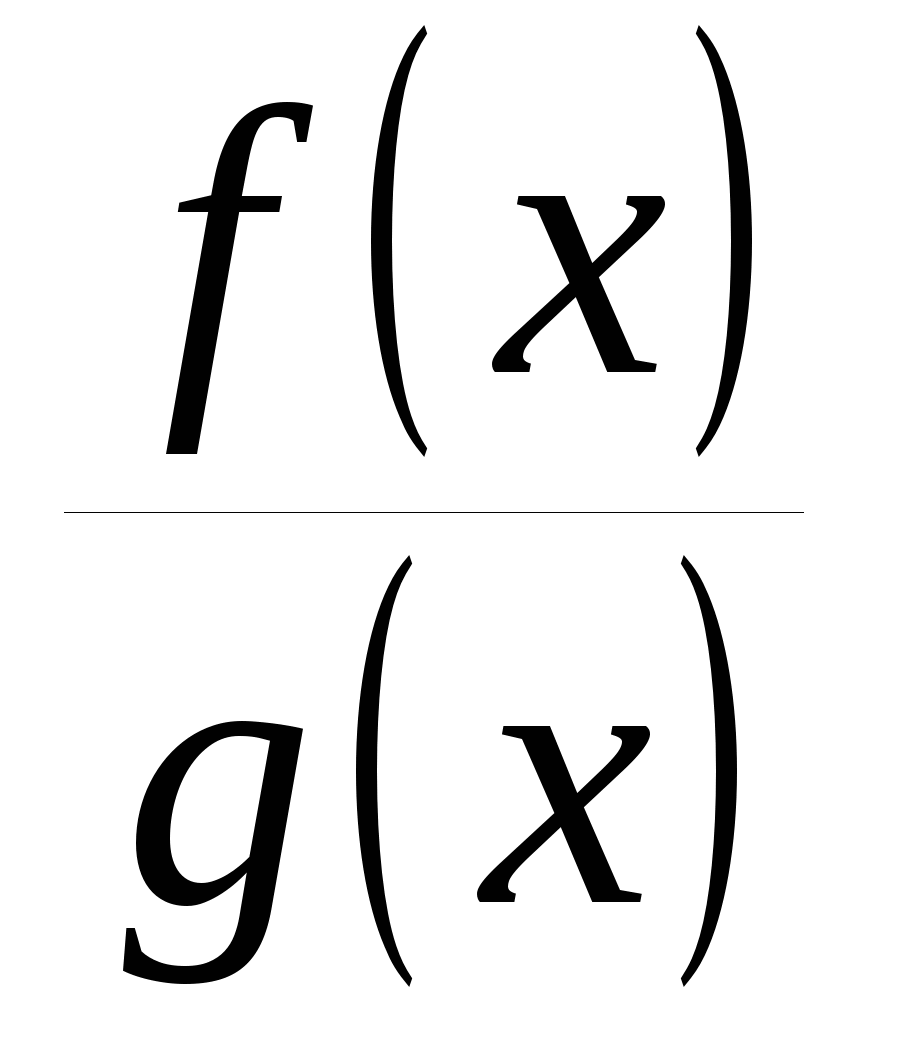 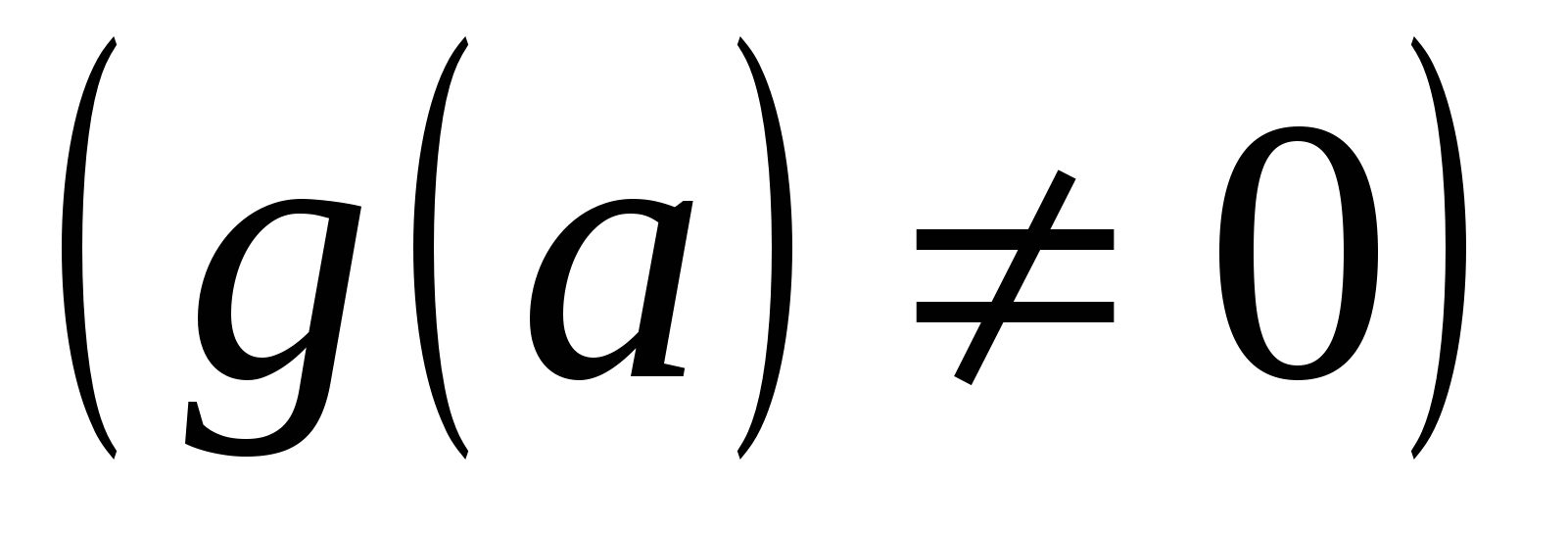 являются функциями, непрерывными в точке a. являются функциями, непрерывными в точке a.
Доказательство следует из определения непрерывности функции и аналогичных свойств пределов функций. ■
♦ 2) Если функция 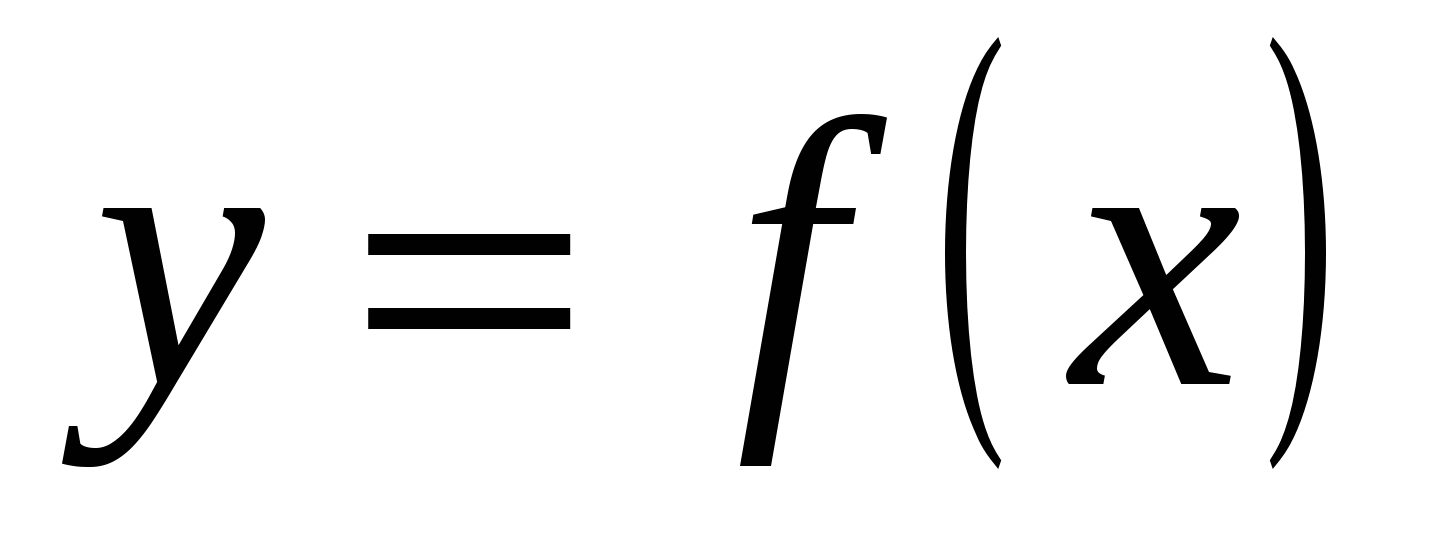 непрерывна в точке а и непрерывна в точке а и 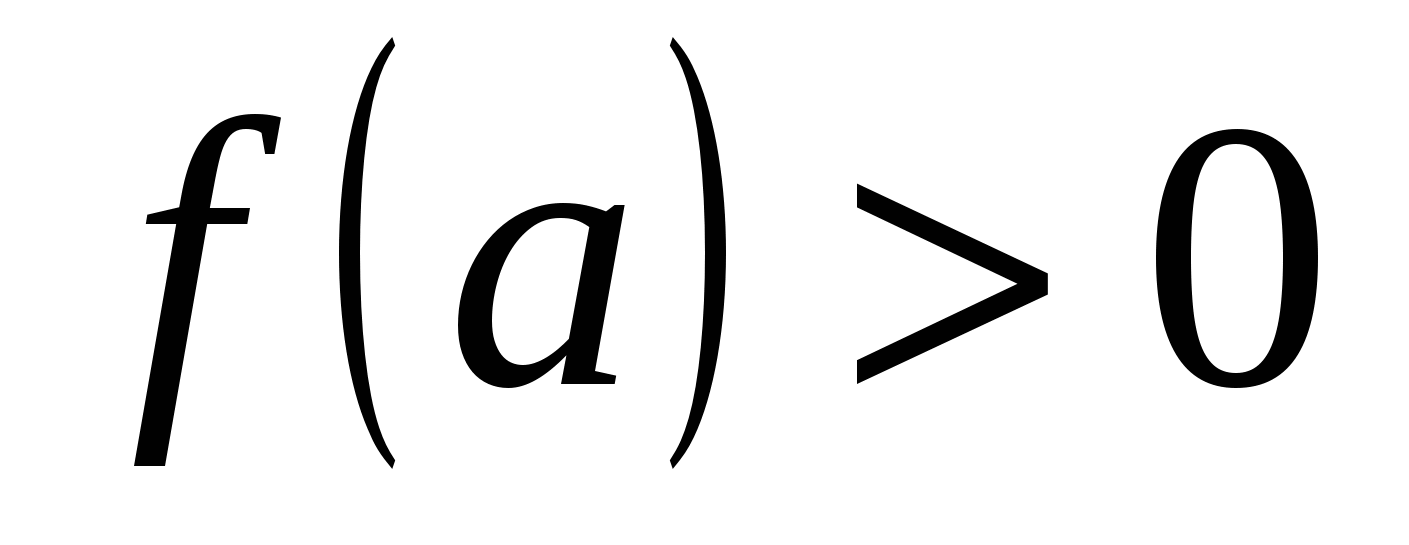 , то существует такая окрестность точки а, в которой , то существует такая окрестность точки а, в которой 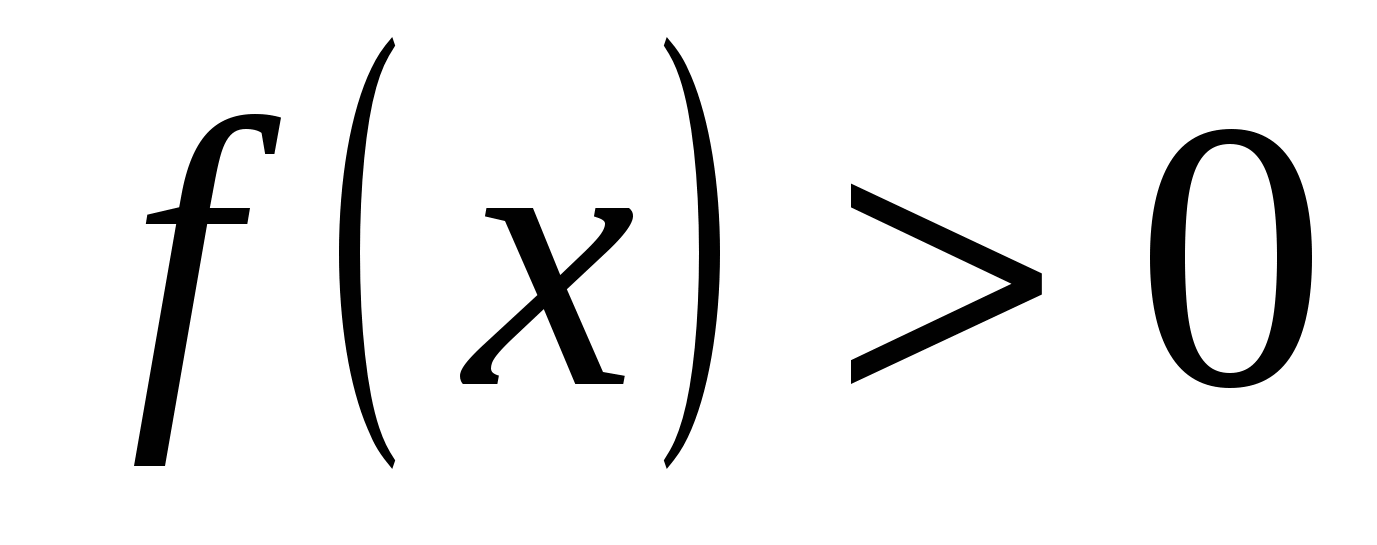 . .
Доказательство этого свойства основывается на том, что при малых приращениях аргумента 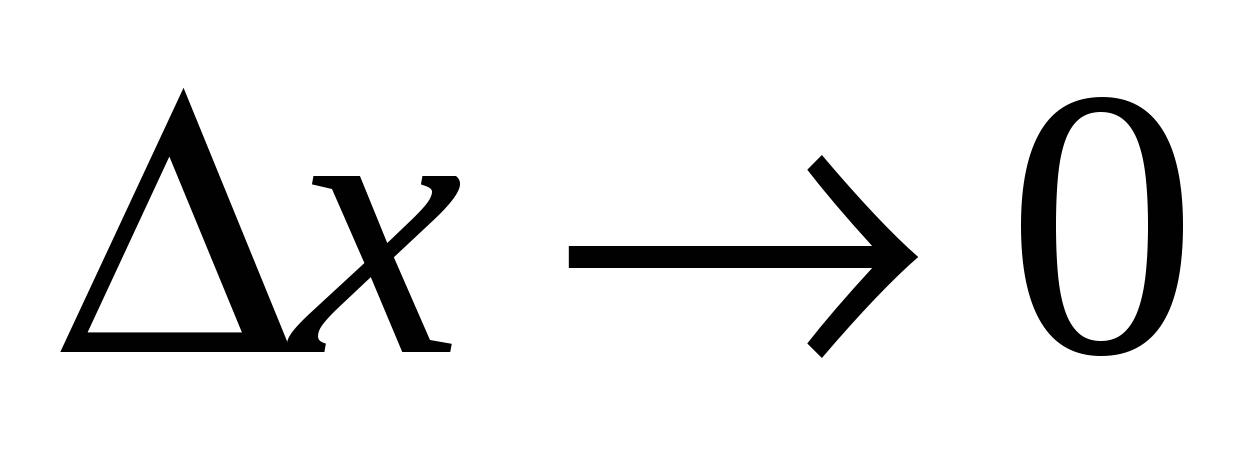 в соответствии с определением 14.3 можно получить как угодно малое приращение функции в соответствии с определением 14.3 можно получить как угодно малое приращение функции  , так что знак функции , так что знак функции 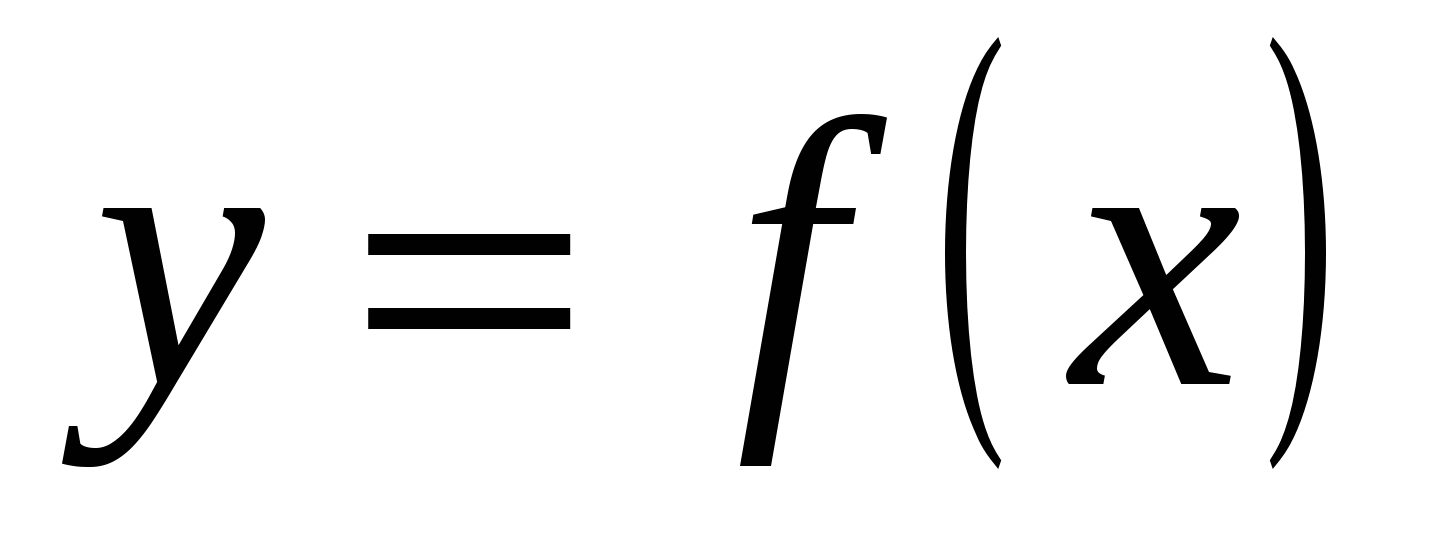 в окрестности точки а не изменится. ■ в окрестности точки а не изменится. ■
♦ 3) Если функция 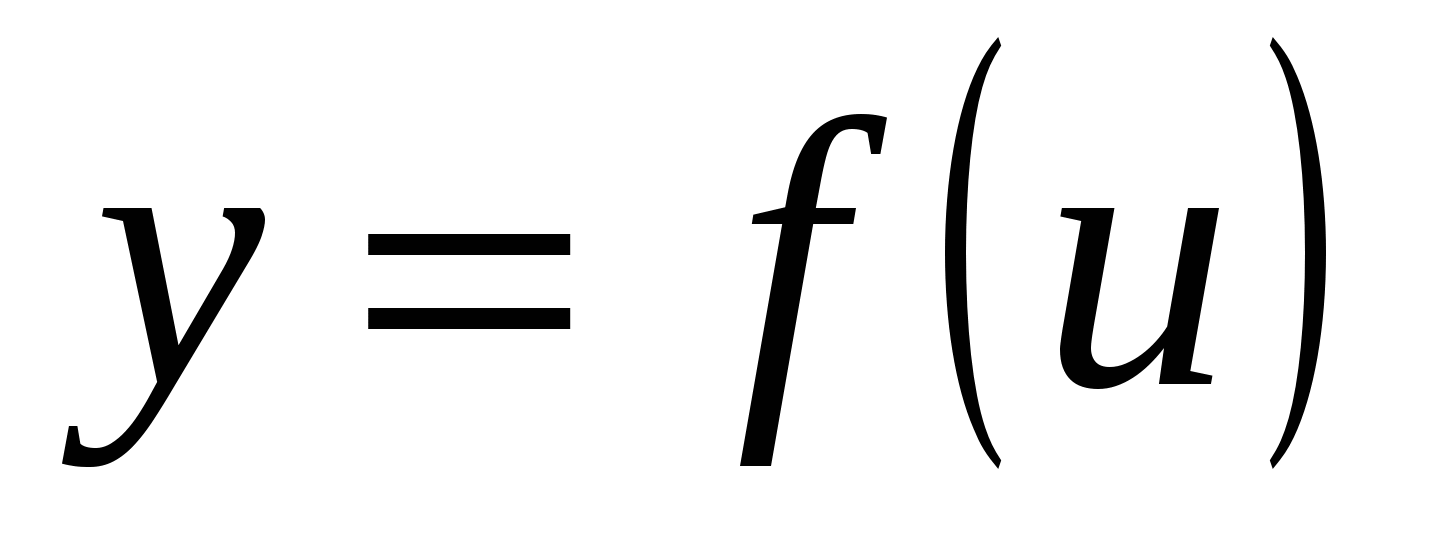 непрерывна в точке непрерывна в точке 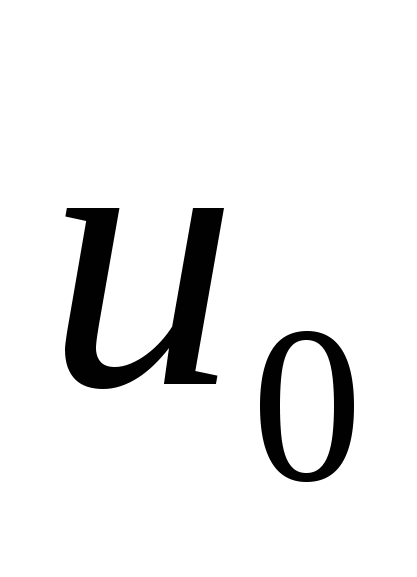 , а функция , а функция 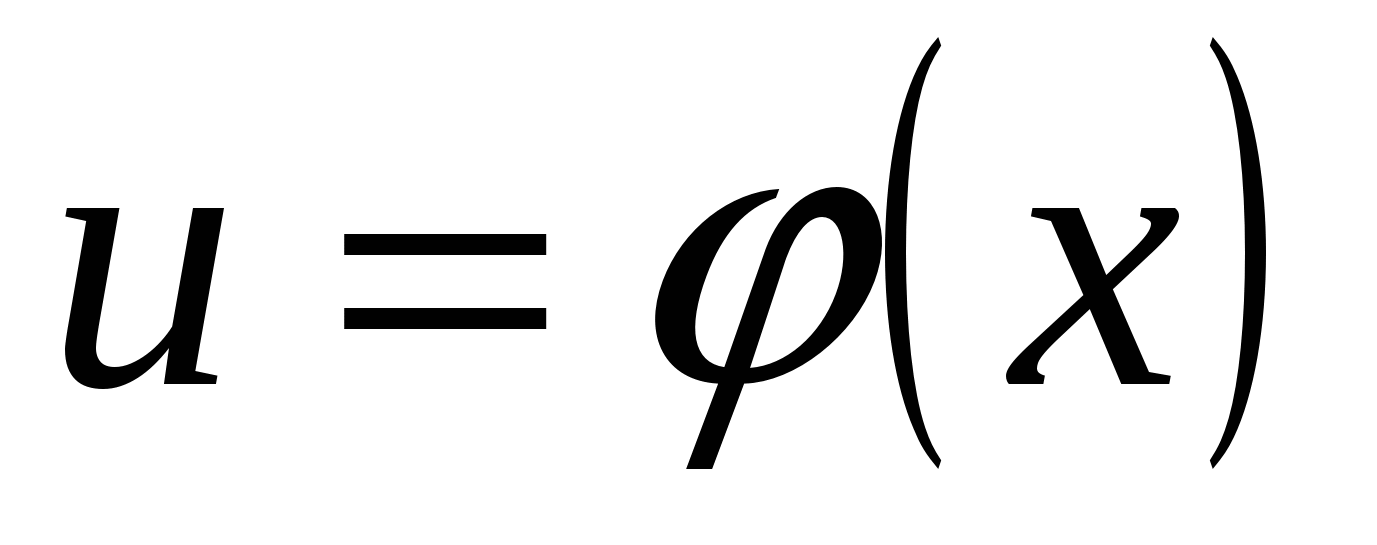 непрерывна в точке непрерывна в точке 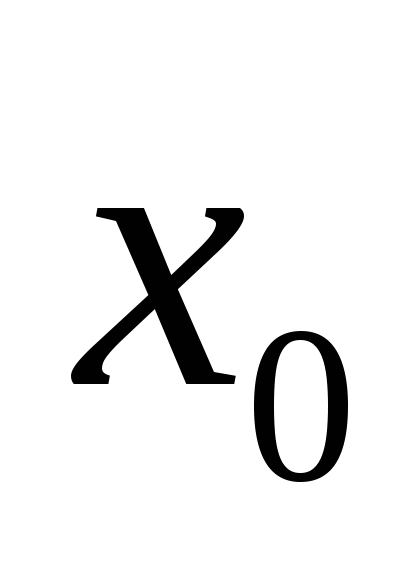 , и , и 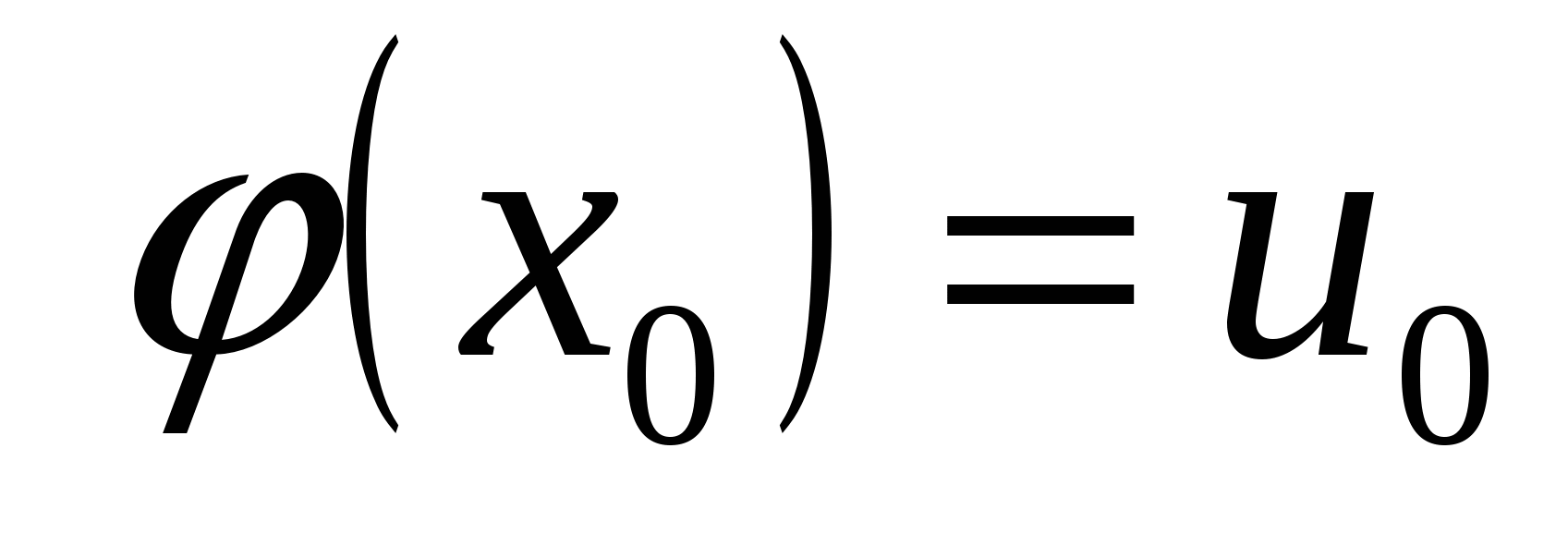 , то сложная функция , то сложная функция 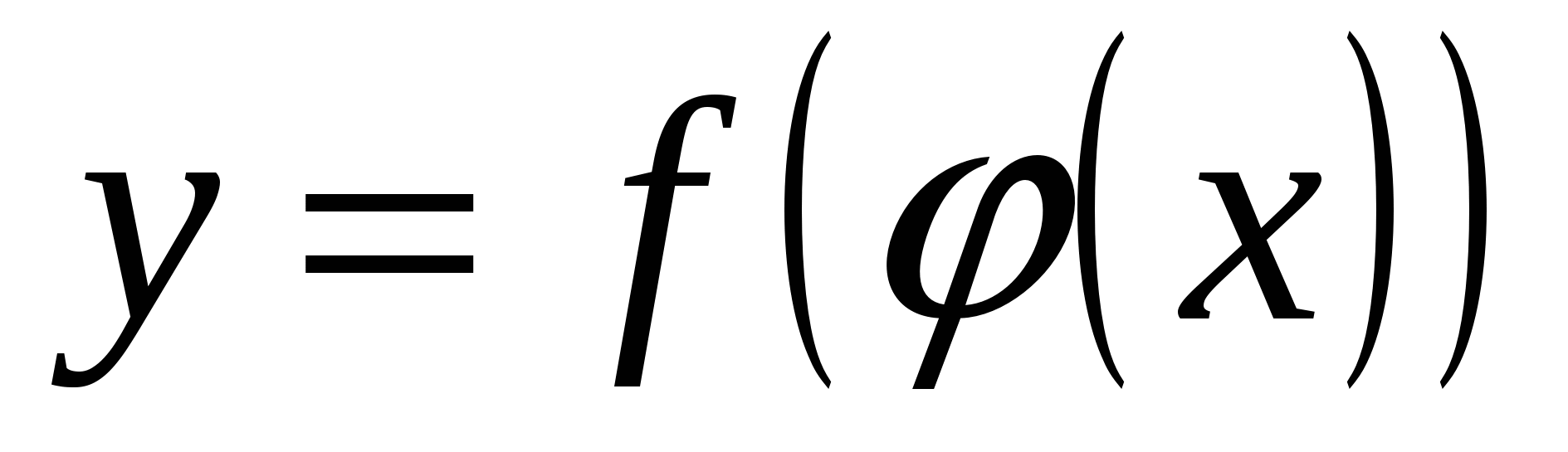 непрерывна в точке непрерывна в точке 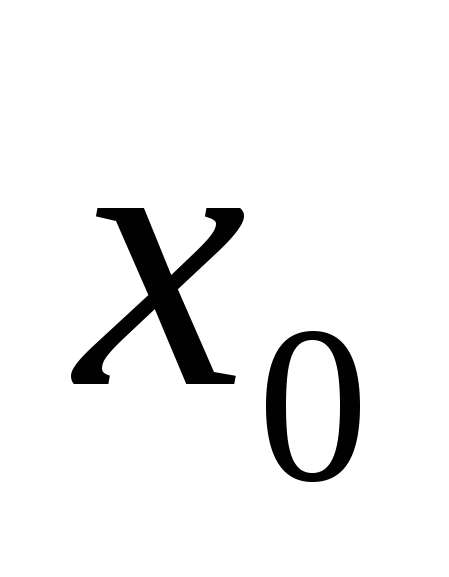 . .
Доказательство. Малому приращению аргумента 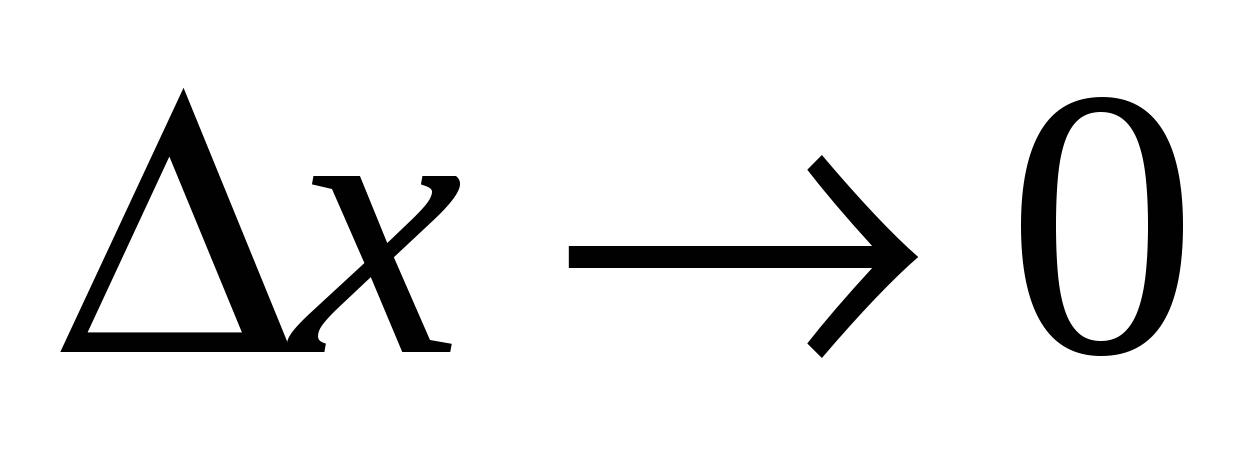 в силу определения 14.3 соответствует как угодно малое приращение в силу определения 14.3 соответствует как угодно малое приращение 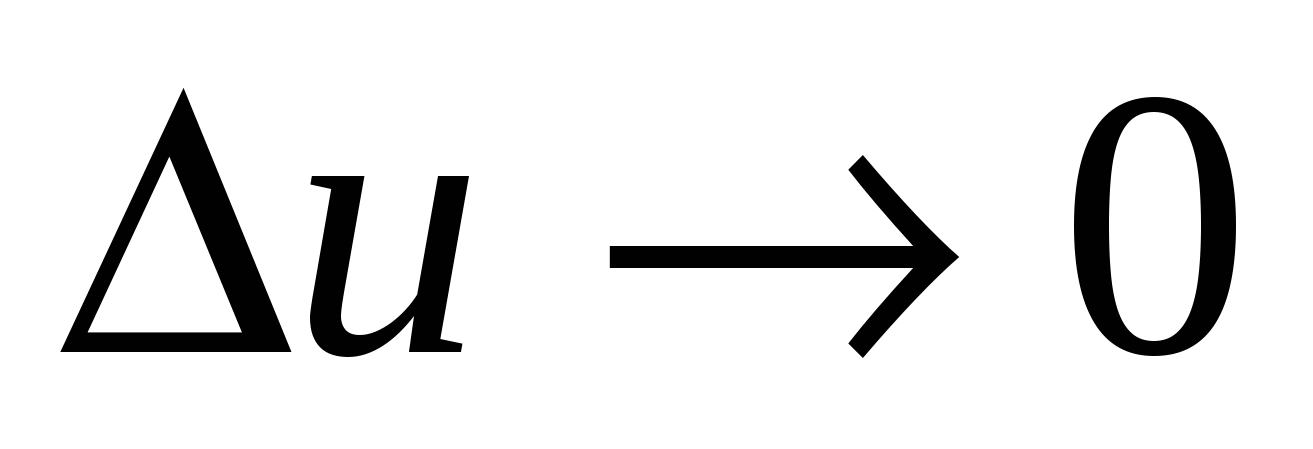 , приводящее, в свою очередь, в силу того же определения непрерывности функции , приводящее, в свою очередь, в силу того же определения непрерывности функции 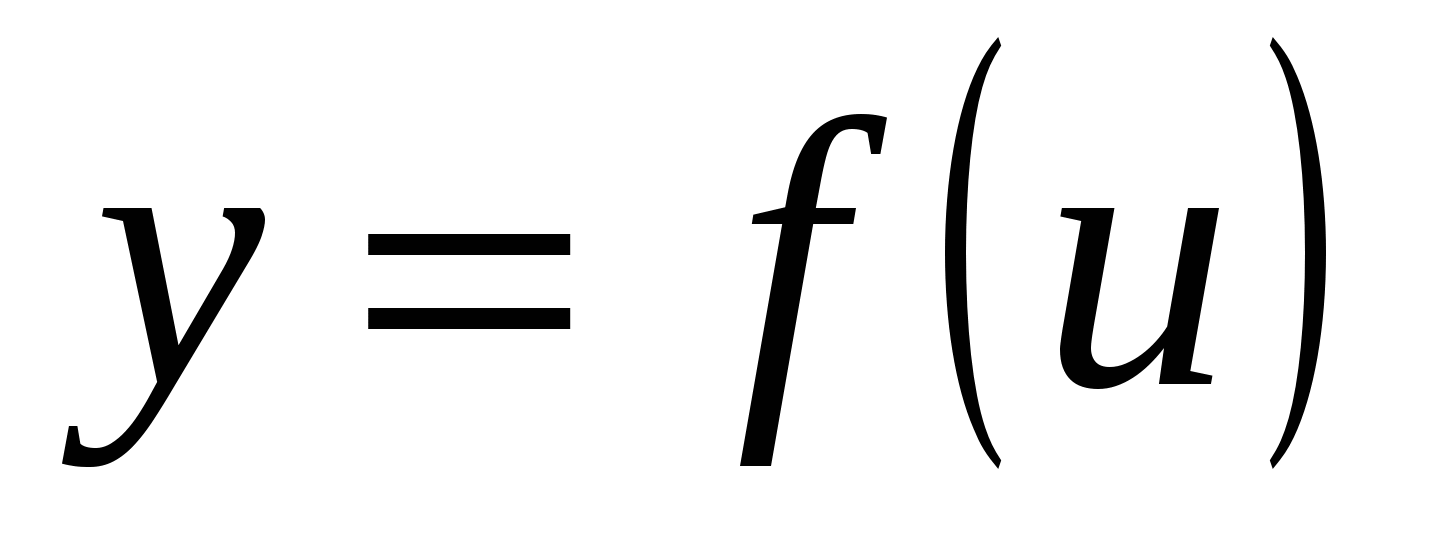 к как угодно малому приращению к как угодно малому приращению 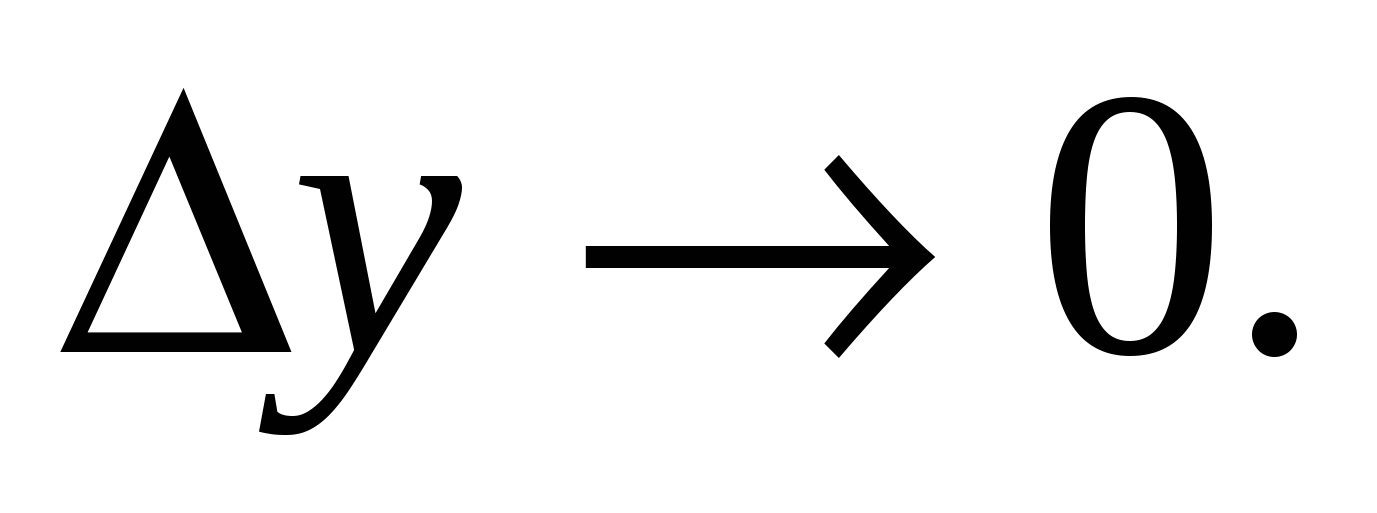 ■ ■
Свойство 3 может быть записано в виде
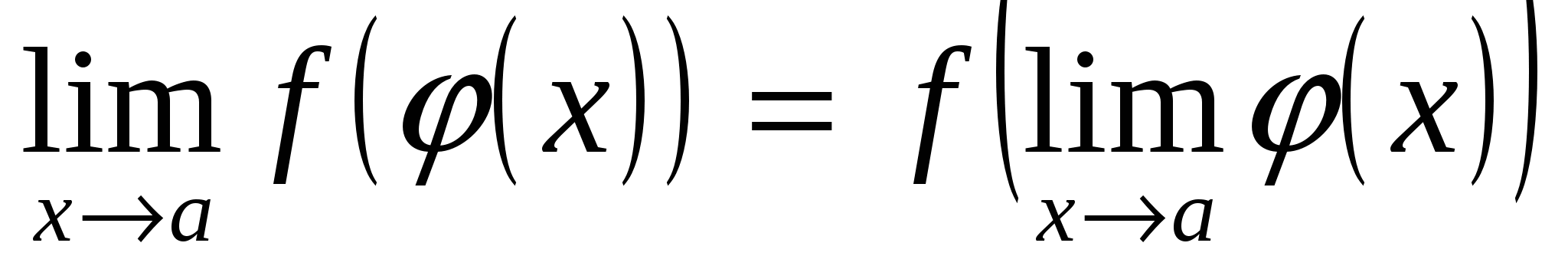 , ,
то есть под знаком сложной функции можно переходить к пределу.
Функция 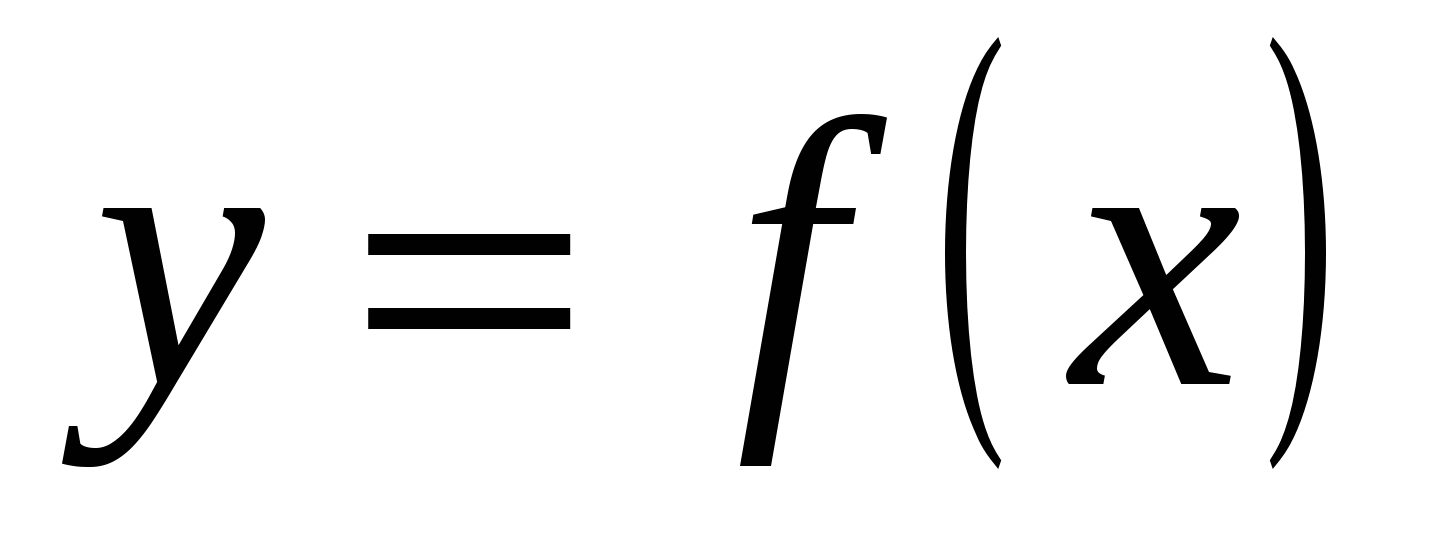 называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны в области их определения. называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны в области их определения.
Пример 14.3. Доказать непрерывность функции 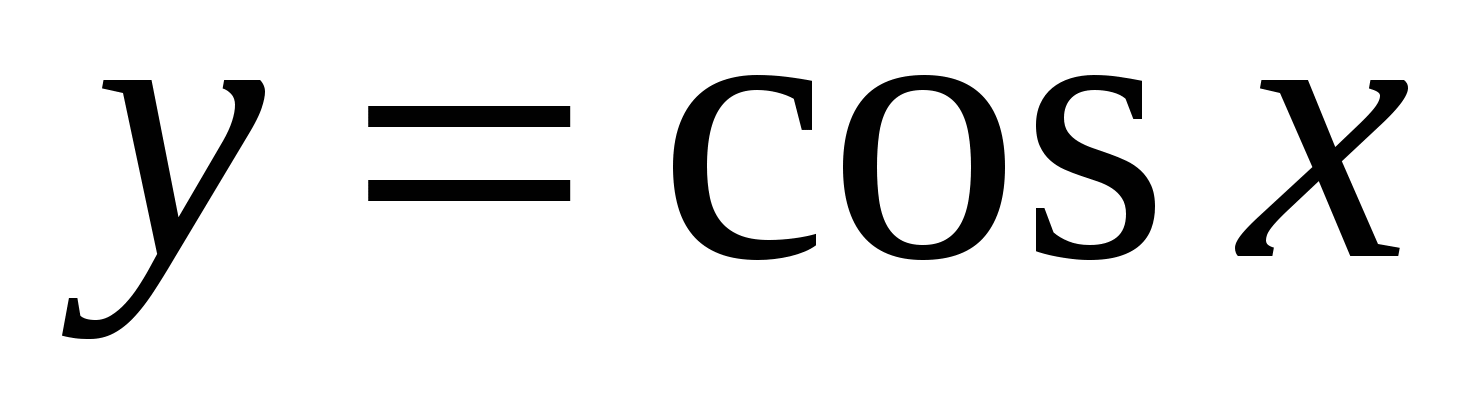 . .
Найдём 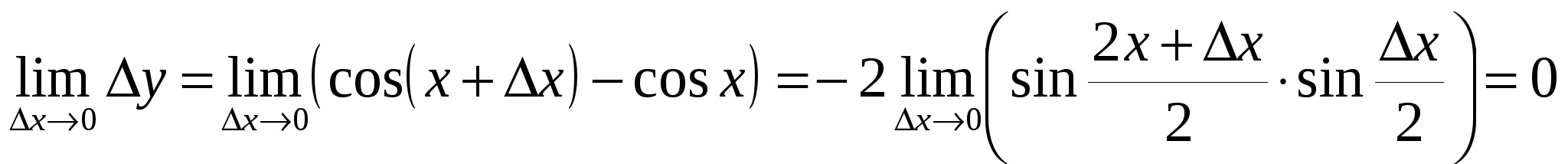 . Таким образом, получили, что . Таким образом, получили, что 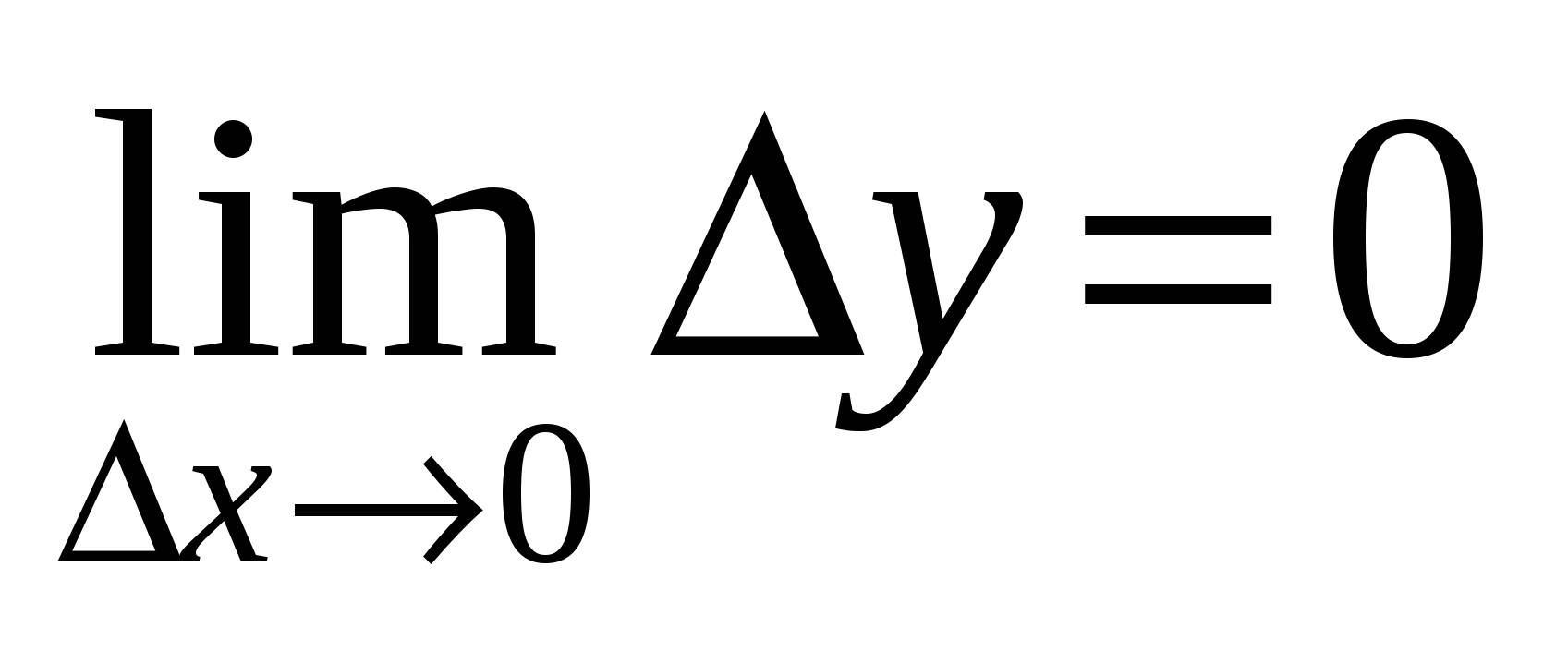 , следовательно, по определению 14.3 функция , следовательно, по определению 14.3 функция 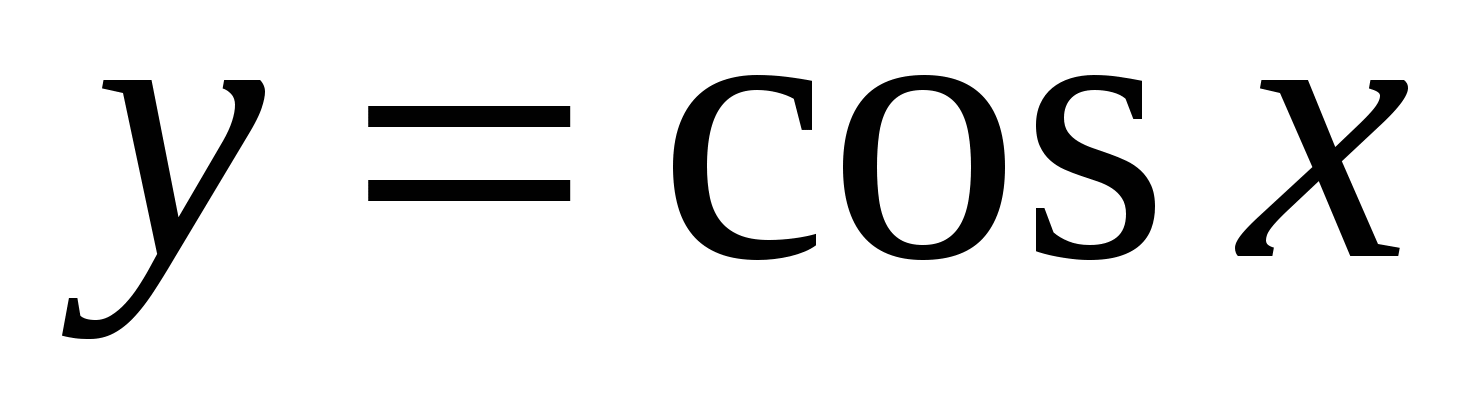 является непрерывной на всей числовой оси. является непрерывной на всей числовой оси.
Отметим ещё некоторые свойства функций, непрерывных на отрезке:
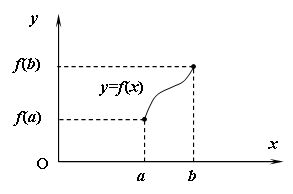
1) Если функция 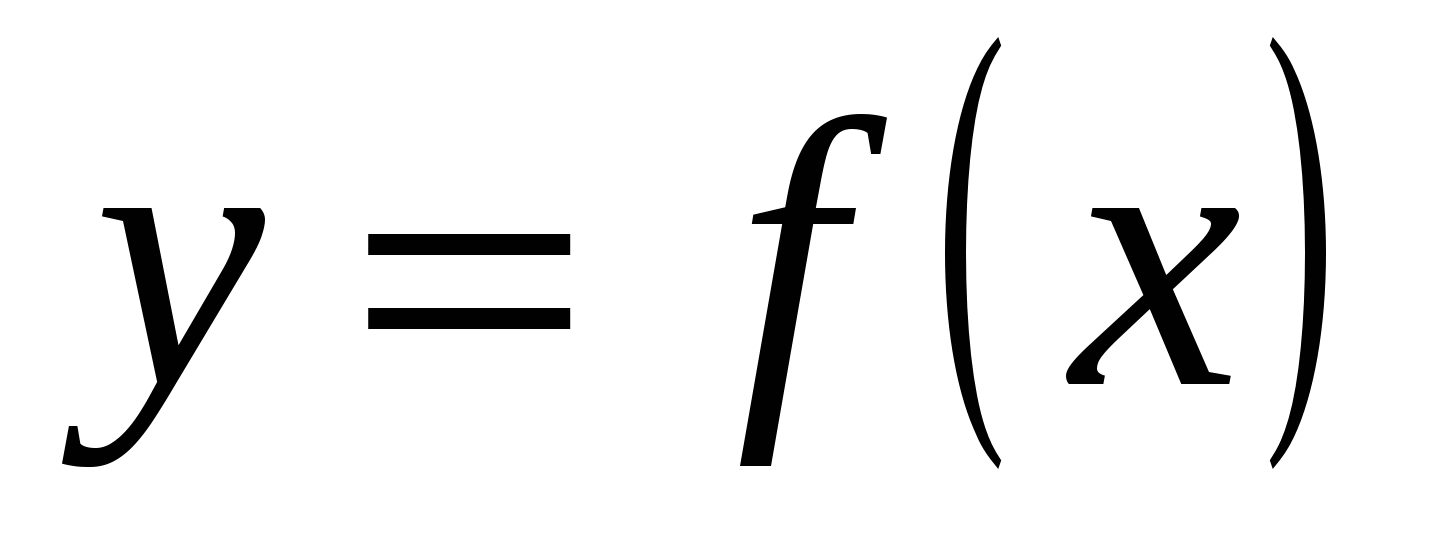 непрерывна на отрезке непрерывна на отрезке 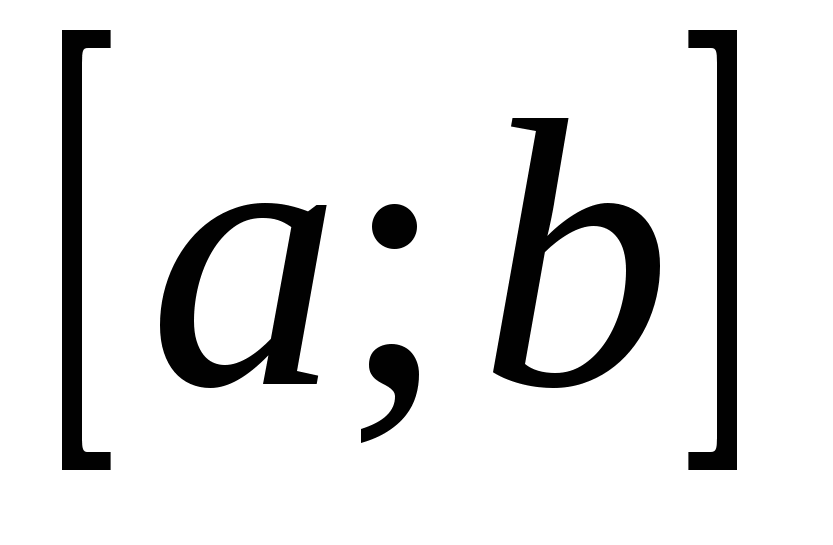 , то она ограничена на этом отрезке (см. рис. 14.5). , то она ограничена на этом отрезке (см. рис. 14.5).
|
|
|
Рис. 14.5.
|
|
|
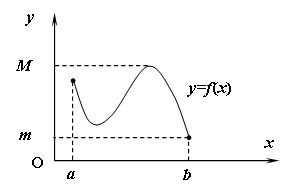
2) Если функция 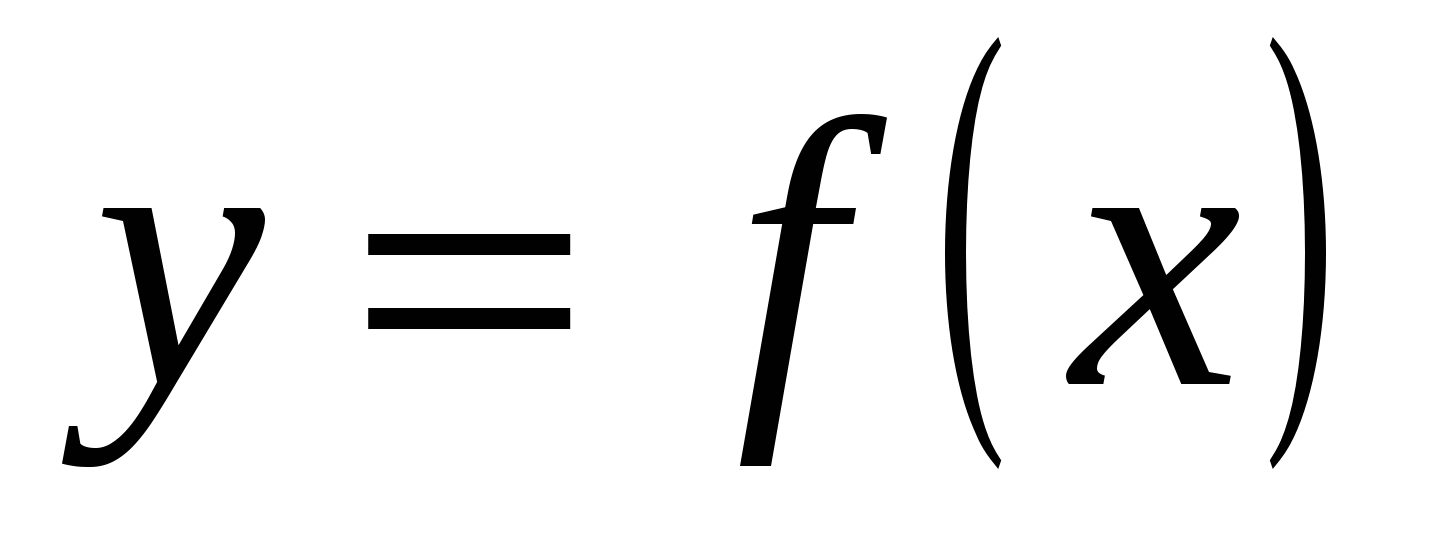 непрерывна на отрезке непрерывна на отрезке 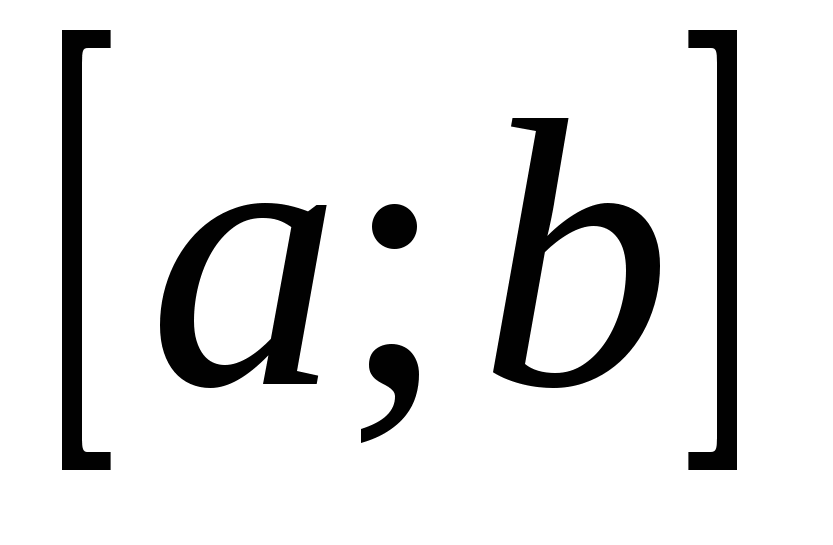 , то она достигает на этом отрезке наименьшего значения m и наибольшего значения M (см. рис. 14.6). , то она достигает на этом отрезке наименьшего значения m и наибольшего значения M (см. рис. 14.6).
|
|
|
Рис. 14.6.
|
|
|
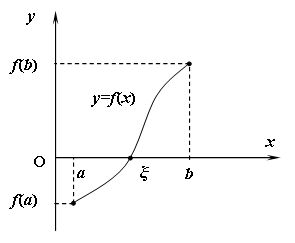
3) Если функция 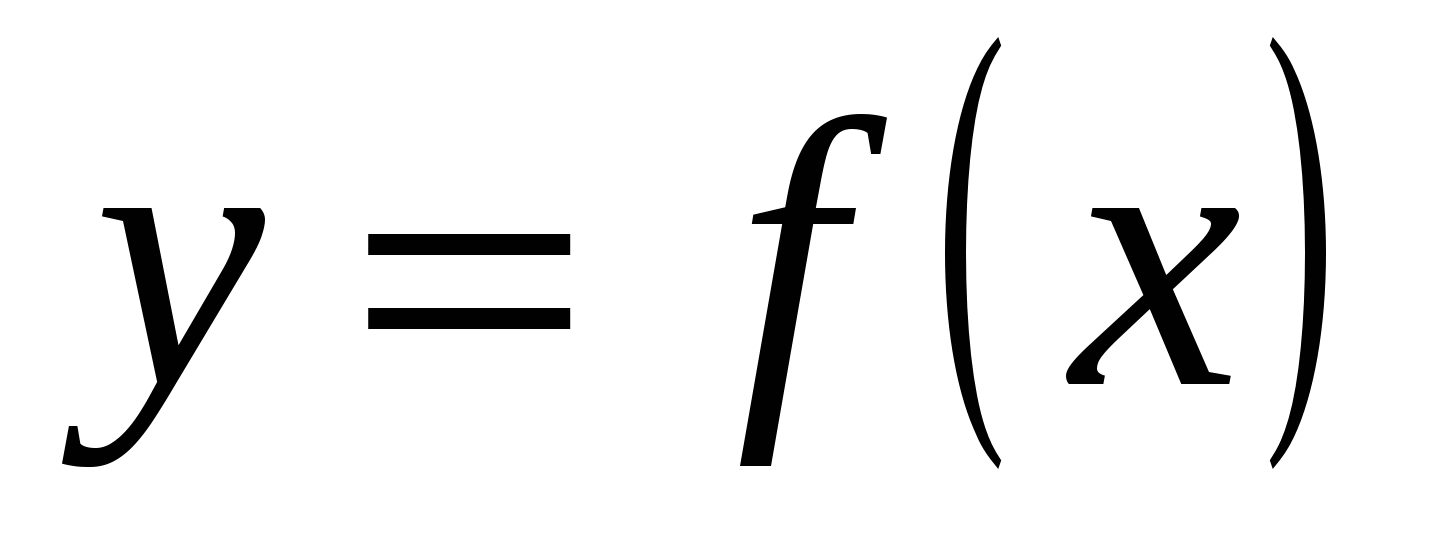 непрерывна на отрезке непрерывна на отрезке 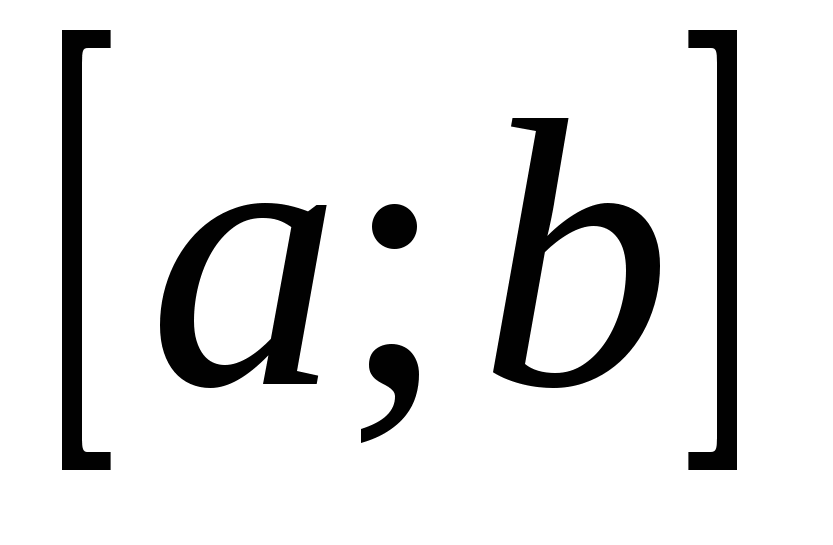 и значения её на концах отрезка и значения её на концах отрезка 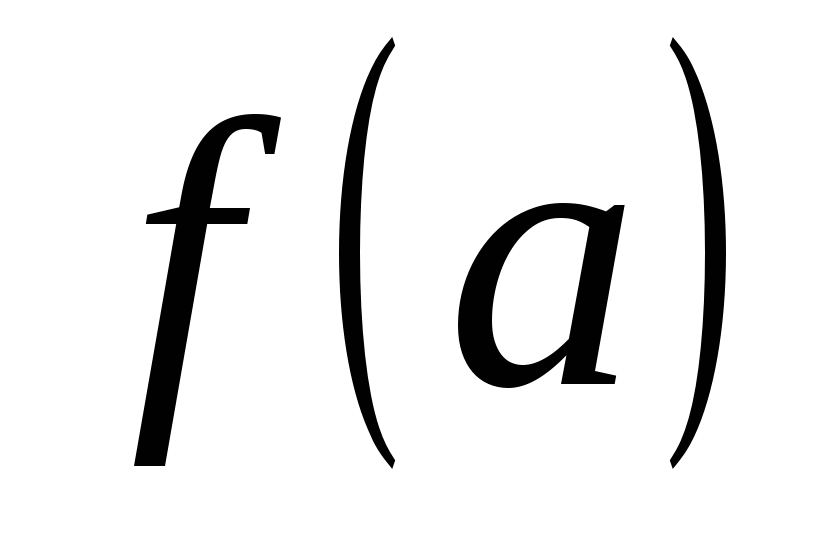 и и 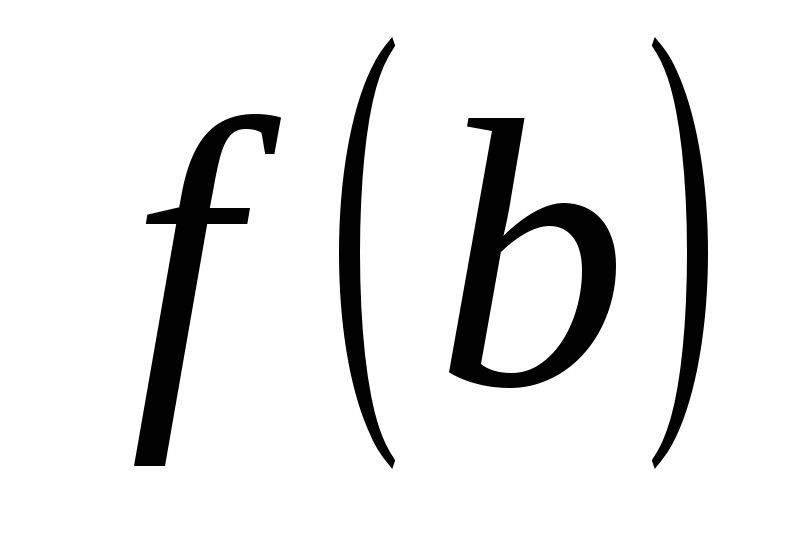 имеют противоположные знаки, то внутри отрезка найдётся точка имеют противоположные знаки, то внутри отрезка найдётся точка 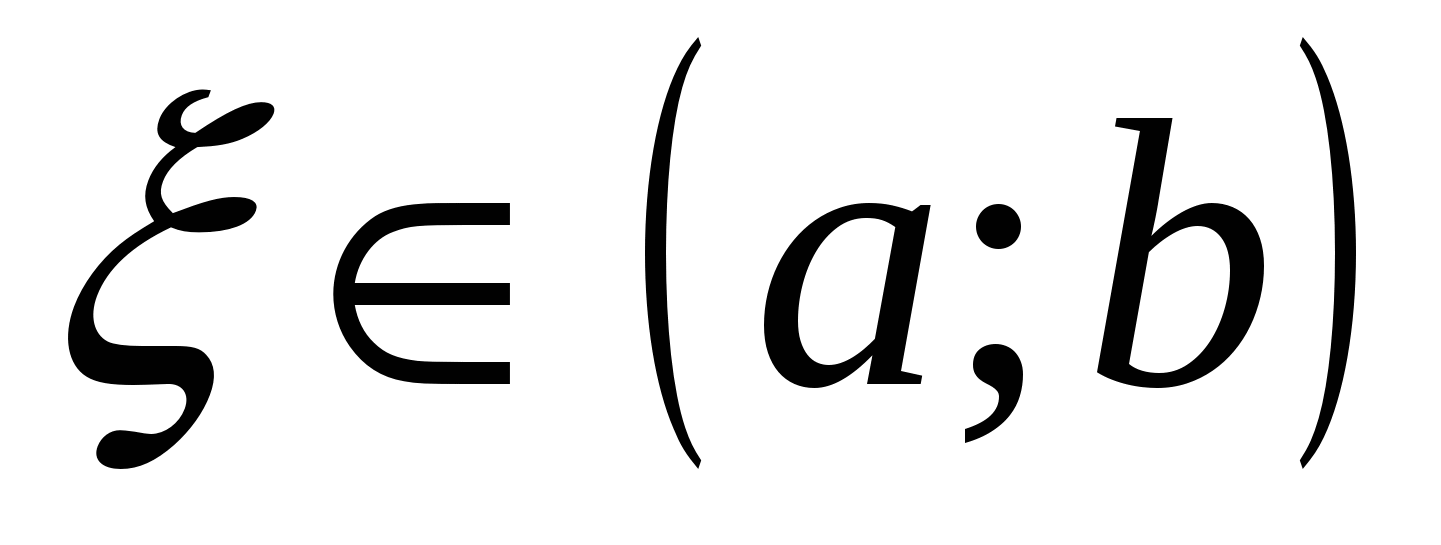 такая, что такая, что 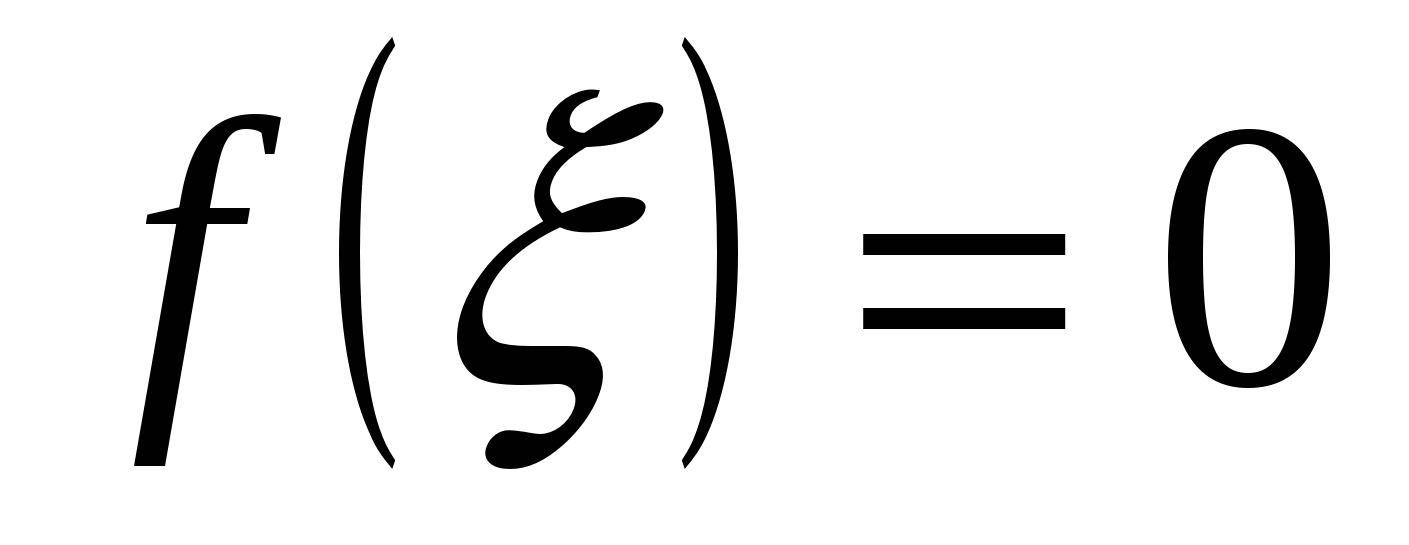 (cм. рис. 14.7). (cм. рис. 14.7).
|
|
|
Рис. 14.7.
|
|
|
|
 Скачать 273.5 Kb.
Скачать 273.5 Kb.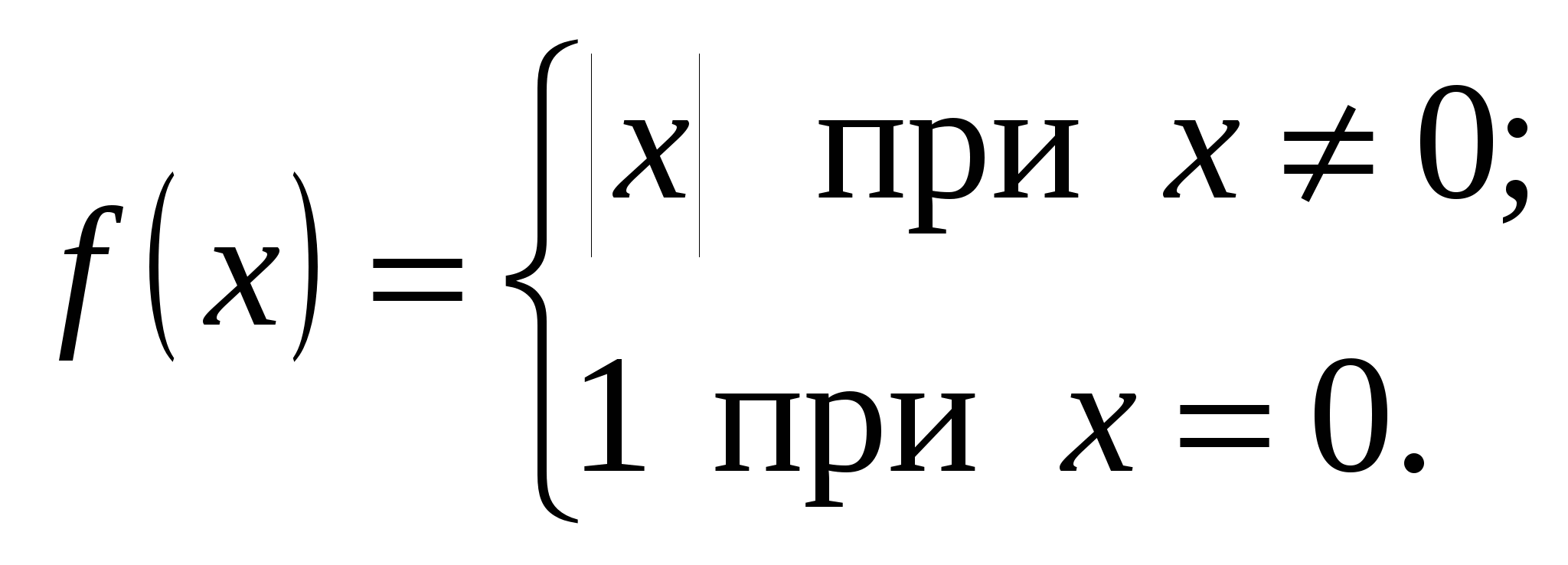 Очевидно,
Очевидно, 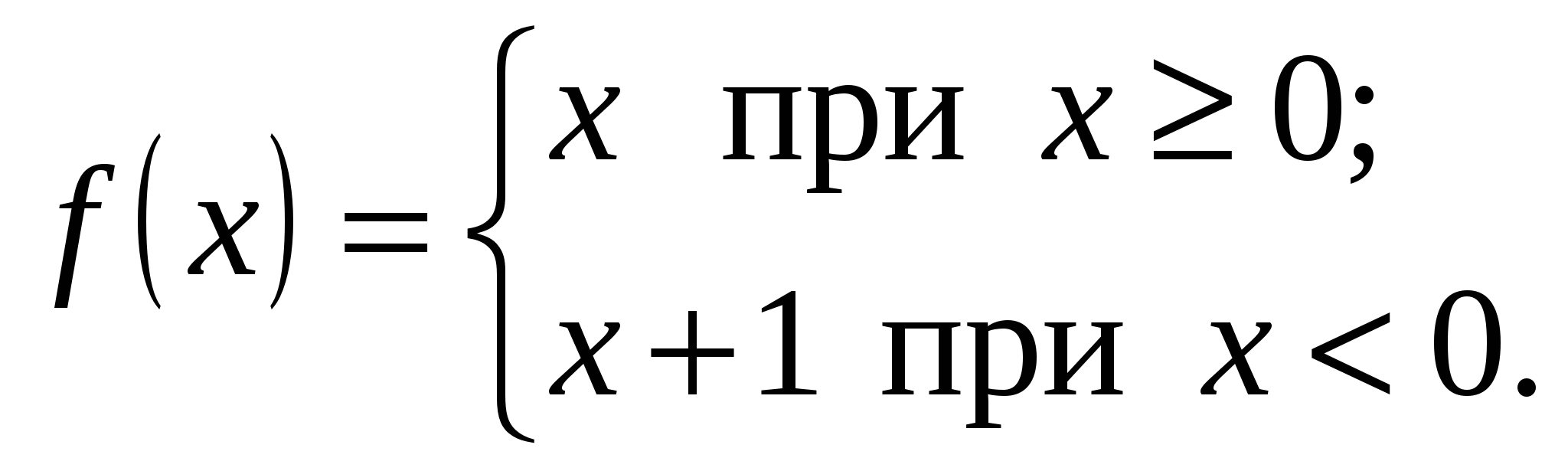 Здесь
Здесь 






