Вопросы по Теме 4 Введение в математический анализ
Определение функции. Способы задания функции.
X и Y – числовые множества, если в силу некоторого закона f любому числу x принадлежащему X поставлена в соответствие одно число y принадлежащие Y, то говорят, что на множестве X задана функция одной переменной x.
1 способ – табличный
2 способ – графический
3 способ – Аналитический
Как определить четность функции?
Функция y=f(x) называется чётной, если она определена на множестве симметричном относительно нулевой точки и обладает свойством f(-x)=f(x)
Какие функции называются монотонными?
Возрастающие, строго возрастающие, убывающие и строго убывающие функции на множестве D1 , называются монотонными, а функции строго возрастающие и строго убывающие называются строго монотонными.
Что такое суперпозиция функций?
Если функция f отображает множество X в Y, а функция g отображает Y в Z, то функцию z=g(f(x)) называют сложной функцией или же суперпозицией функций f и g.
Как определить периодичность функции?
Чтобы найти период функции y=a*f(kx+b), где a,k,b некоторые числа, необходимо воспользоваться формулой 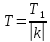 , где T1 – период функции f(x), и f(x) периодичная функция. , где T1 – период функции f(x), и f(x) периодичная функция.
Чтобы найти период функции являющейся суммой 2-х и более функций нужно найти наименьшее общее кратное периодов сложенных функций T=НОК(T1;T2;…;Tn)
Какая функция называется ограниченной?
Функция y=f(x) называется ограниченной если существует такое число M∈R, такое, что для любых x∈D выполняется неравенство f(x)≥(≤)М.
Нахождение функции, обратной для данной.
Чтобы найти обратную функцию, необходимо решить уравнение y=f(x) относительно x.
Какая функция называется строго возрастающей, а какая - возрастающей?
Если f(x1)
Если f(x1)≤f(x2), то функция называется возрастающей на множестве D1
Какая функция называется ограниченной сверху?
Функция y=f(x) называется ограниченной сверху, если существует такое число M∈R, что для любых x∈D выполняется неравенство f(x)≤М.
Какая функция называется ограниченной снизу?
Функция y=f(x) называется ограниченной снизу, если существует такое число M∈R, что для любых x∈D выполняется неравенство f(x)≥М.
Основные элементарные функции.
1) Степенные функции (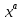 ,где а любое фиксированное число) ,где а любое фиксированное число)
2) Логарифмические (y=logax, где a>0 и а неравно 1)
3)Показательные (y=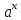 где a>0 и a неравно 1) где a>0 и a неравно 1)
4)Тригонометрические (y=sin;cos;tg;ctg(x))
5)обратные тригонометрические (y=arcsin;arcos;arctg;arcctg(x))
6)Постоянные функции (y=c, где c любое число)
Какая функция называется строго убывающей, а какая - убывающей?
Если f(x1)>f(x2), то функция называется строго убывающей на множестве D1
Если f(x1)≥f(x2), то функция называется убывающей на множестве D1
Построение графиков функций.
Зададим на некотором интервале (a;b) функцию y=f(x), тогда:
1) y=p*f(x), где p>0 и p не равно 1, также определенна на (a;b) и при p>1 график функции растянут в p раз вдоль оси Oy; при p<1 график функции сжат в 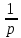 раз вдоль оси Oy. раз вдоль оси Oy.
2)Функция y=f(kx), где k>0 и k не равно 1, определена на интервале 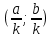 , и при k>1 график функции сжат в k раз вдоль оси Ox, если k<1 график функции растянут в , и при k>1 график функции сжат в k раз вдоль оси Ox, если k<1 график функции растянут в  раз вдоль оси Ox. раз вдоль оси Ox.
3)y=f(x)+c определена на интервале (a;b) и при c>0 график функции смещён вверх на величину c, при c<0 вниз на туже величину c.
4)y=f(x-d) получается из графика функции y=f(x) путём смещения на величину d вправо, если d>0 и влево, если d<0 вдоль оси Ox.
5)y=-f(x) является зеркальным отражением графика функции y=f(x) относительно оси Ox.
6)y=f(-x) зеркальное отображение графика функции y=f(x) вдоль оси Oy.
Понятие предела функции.
Число А называется приделом функции y=f(x), при x стремящимся к бесконечности, если для любого сколь угодного ε>0 найдётся такое положительное число δ= δ(ε), что для всех x, таких, что 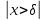 , верно , верно 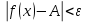 . .
Понятие бесконечно малых и бесконечно больших функций.
Функция α(x) называется бесконечно малой в точке  (x→ (x→ ), если ), если 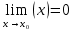 . Аналогично формулируется определение бесконечно малой функции при x→∞. . Аналогично формулируется определение бесконечно малой функции при x→∞.
Функция α(x) называется бесконечно большой в точке  (x→ (x→ ), если ), если 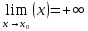 . Аналогично формулируется определение бесконечно большой функции при x→∞. . Аналогично формулируется определение бесконечно большой функции при x→∞.
Основные свойства бесконечно малых и бесконечно больших функций.
1) Алгебраическая сумма, произведение конечного числа бесконечно малых в окрестности точки  функций, есть бесконечно малые функции. функций, есть бесконечно малые функции.
2) Произведение Бм на ограниченную в окрестности точки  функцию, есть Бм функция. функцию, есть Бм функция.
3) Частное от деления Бм в окрестностях точки  функции на функцию имеющую в этой точке ненулевой придел, есть Бм функция. функции на функцию имеющую в этой точке ненулевой придел, есть Бм функция.
4) Произведение Бб в окрестностях точки  функции на функцию имеющую в этой точке ненулевой придел, есть Бб функция. функции на функцию имеющую в этой точке ненулевой придел, есть Бб функция.
5) Сумма Бб в окрестностях точки  функции и ограниченной функции в этой окрестности, есть Бб функция. функции и ограниченной функции в этой окрестности, есть Бб функция.
6) Частное от деления Бб в окрестности точки  функции на функцию имеющую в этой точке ненулевой придел, есть Бб функция. функции на функцию имеющую в этой точке ненулевой придел, есть Бб функция.
Понятие односторонних пределов функции.
Приделы слева и справа называются односторонними приделами. Для существования некоторого придела функции y=f(x) в точке   , необходимо и достаточно, чтобы оба односторонних придела в точке , необходимо и достаточно, чтобы оба односторонних придела в точке  существовали и были равны А. существовали и были равны А.
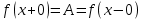 . .
Сравнение бесконечно малых и бесконечно больших функций.
Для сравнения Бм функций a(x) и b(x) при x→ находят придел их отношений находят придел их отношений 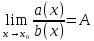
Бб функции сравниваются по такому же принципу что и Бм функции.
Таблица «Арифметика бесконечных величин».
0 – Бм величина
а-const
|
∞ - Бб величина
а-const
|
Неопределённости
|
1)0+0=0
2)0-0=0
3)а+0=а
4)а-0=а
5)0*0=0
6)а*0=0
7) 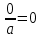 , при а неравном 0 , при а неравном 0
8) 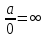 , при а неравном 0 , при а неравном 0
9) 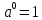 (a>0, а неравно 1) (a>0, а неравно 1)
10) 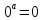
11) 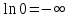
|
1)∞+∞=∞
2)а+∞=∞
3)∞*∞=∞
4)а*∞=∞ (а неравно 0)
5)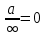
6)
7)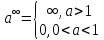
8)
9)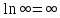
|
1)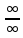
2)
3)∞-∞
4)0*∞
5)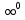
6)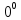
|
Основные теоремы о пределах.
Теорема 1- Придел алгебраической суммы функций равен алгебраической сумме приделов этих функций.
Теорема 2 – Придел произведения функций равен произведению приделов этих функций.
Теорема 3 – Придел частного двух функций равен частному приделов этих функций.
Теорема 4 – Если C-const, то придел С равен С.
Теорема 5 – Постоянный множитель С можно выносить за знак придела.
Теорема 6 – Если придел функции f(x) существует, то он единственен.
Теорема 7 – Если функция y=f(x) определенна в точке  и является элементарной функцией, то её придел равен значению функции в этой точке. и является элементарной функцией, то её придел равен значению функции в этой точке.
Теорема 8 – Пусть в некоторой проколотой окрестности точки  выполняется неравенство f(x)≤h(x)≤φ(x), тогда если выполняется неравенство f(x)≤h(x)≤φ(x), тогда если 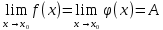 , то и , то и 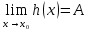 . .
Первый замечательный предел.

Следствия из первого замечательного предела.
1)
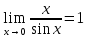
2)
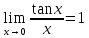
3)
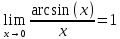
4)
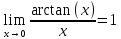
Второй замечательный предел.

Следствия из второго замечательного предела.
1)
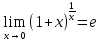
2)
 , a>0, a неравно 1 , a>0, a неравно 1
3)
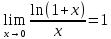
4)
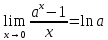 , a>0, a неравно 1 , a>0, a неравно 1
5)
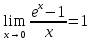
6)
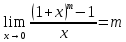 , m неравно 0 , m неравно 0
Сформулировать теорему о замене бесконечно малых на эквивалентные.
Если y = f(x) и y = g(x) Бм функции в точке  и и
1)
f(x) f1(x), g(x) g1(x)
2)

Тогда следует что 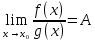
Таблица эквивалентных бесконечно малых функций.
1)sinλ(x) λ(x)
2)tgλ(x) λ(x)
3)arcsinλ(x) λ(x)
4)arctgλ(x) λ(x)
5)1-cosλ(x) 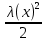
6)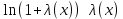
7)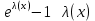
8)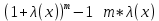 , при m не равном 0 , при m не равном 0
9)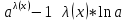 , (a>0, a не равно 1) , (a>0, a не равно 1)
10)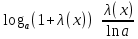 , (a>0, a не равно 1) , (a>0, a не равно 1)
Способы раскрытия неопределенности вида  . .
1) Деление числителя и знаменателя на старшую степень x.
2) Замена Бб функций на эквивалентные.
Способы раскрытия неопределенности вида 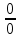 . .
1) Разложение на множители многочленов числителя и(или) знаменателя.
2) Умножение числителя и знаменателя дроби, на выражение сопряженное к числителю и(или знаменателю)(дополнение до разности квадратов или кубов)
3) Использование первого замечательного предела и следствий.
4) Замена Бм функций на эквивалентные.
Способы раскрытия неопределенности вида 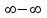 . .
1) Умножение и деление на сопряжённое выражение.
2) Приведение выражения под знаком предела к общему знаменателю.
Способы раскрытия неопределенности вида 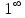 . .
1) Использование 2-го замечательного предела и следствий
2) Использование логарифмического тождества
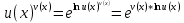
Раскрытие неопределенностей вида 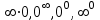 . .
Сводятся путём тождественных преобразований к способам раскрытий неопределённостей 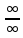 , ,  , , 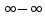 , , 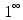 или решаются другими способами. или решаются другими способами.
Какая функция называется непрерывной в точке x0?
Функция y=f(x) определённая в некоторой окрестности точки  называется непрерывной в точке называется непрерывной в точке  , если существует конечный предел функции в этой точке и он равен значению функции в этой точке. , если существует конечный предел функции в этой точке и он равен значению функции в этой точке.
Какая функция называется непрерывной на отрезке 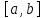 ? ?
Функция называется непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка
Какие точки называются точками разрыва функции?
Точки, в которых нарушается непрерывность функции называются точками разрыва функции.
Понятие точек разрыва первого рода и точек устранимого разрыва.
Если в точке  существует конечные односторонние пределы f(x-0) f(x+0), такие, что существует конечные односторонние пределы f(x-0) f(x+0), такие, что 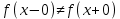 , то точка , то точка  называется точкой разрыва 1-го рода. называется точкой разрыва 1-го рода.
Разрыв называется устранимым, если в точке  существуют точечные односторонние пределы f(x-0) f(x+0) такие, что существуют точечные односторонние пределы f(x-0) f(x+0) такие, что 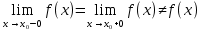 или функция в точке или функция в точке  неопределенна. неопределенна.
Понятие точек разрыва второго рода.
Если хотя бы один из существующих пределов f(x-0), f(x+0) равен бесконечности или не существует, то точка  называется точкой разрыва 2-го рода. называется точкой разрыва 2-го рода. |
 Скачать 44.84 Kb.
Скачать 44.84 Kb.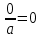 , при а неравном 0
, при а неравном 0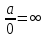 , при а неравном 0
, при а неравном 0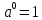 (a>0, а неравно 1)
(a>0, а неравно 1)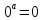
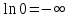
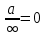

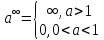

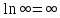
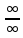

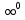
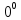
 и является элементарной функцией, то её придел равен значению функции в этой точке.
и является элементарной функцией, то её придел равен значению функции в этой точке. выполняется неравенство f(x)≤h(x)≤φ(x), тогда если
выполняется неравенство f(x)≤h(x)≤φ(x), тогда если 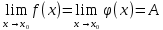 , то и
, то и 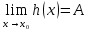 .
.
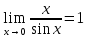
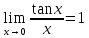
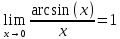
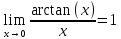

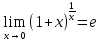
 , a>0, a неравно 1
, a>0, a неравно 1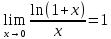
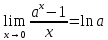 , a>0, a неравно 1
, a>0, a неравно 1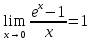
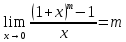 , m неравно 0
, m неравно 0 и
и
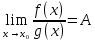
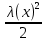
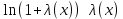
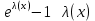
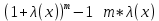 , при m не равном 0
, при m не равном 0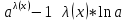 , (a>0, a не равно 1)
, (a>0, a не равно 1)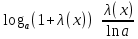 , (a>0, a не равно 1)
, (a>0, a не равно 1) .
.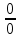 .
.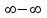 .
.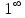 .
.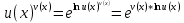
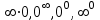 .
.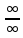 ,
,  ,
, 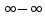 ,
, 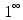 или решаются другими способами.
или решаются другими способами. называется непрерывной в точке
называется непрерывной в точке  , если существует конечный предел функции в этой точке и он равен значению функции в этой точке.
, если существует конечный предел функции в этой точке и он равен значению функции в этой точке.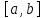 ?
? существует конечные односторонние пределы f(x-0) f(x+0), такие, что
существует конечные односторонние пределы f(x-0) f(x+0), такие, что 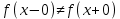 , то точка
, то точка  называется точкой разрыва 1-го рода.
называется точкой разрыва 1-го рода. существуют точечные односторонние пределы f(x-0) f(x+0) такие, что
существуют точечные односторонние пределы f(x-0) f(x+0) такие, что 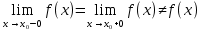 или функция в точке
или функция в точке  неопределенна.
неопределенна. называется точкой разрыва 2-го рода.
называется точкой разрыва 2-го рода.
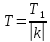 , где T1 – период функции f(x), и f(x) периодичная функция.
, где T1 – период функции f(x), и f(x) периодичная функция.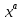 ,где а любое фиксированное число)
,где а любое фиксированное число)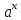 где a>0 и a неравно 1)
где a>0 и a неравно 1)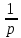 раз вдоль оси Oy.
раз вдоль оси Oy.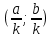 , и при k>1 график функции сжат в k раз вдоль оси Ox, если k<1 график функции растянут в
, и при k>1 график функции сжат в k раз вдоль оси Ox, если k<1 график функции растянут в  раз вдоль оси Ox.
раз вдоль оси Ox.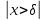 , верно
, верно 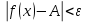 .
.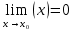 . Аналогично формулируется определение бесконечно малой функции при x→∞.
. Аналогично формулируется определение бесконечно малой функции при x→∞.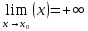 . Аналогично формулируется определение бесконечно большой функции при x→∞.
. Аналогично формулируется определение бесконечно большой функции при x→∞. , необходимо и достаточно, чтобы оба односторонних придела в точке
, необходимо и достаточно, чтобы оба односторонних придела в точке 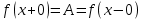 .
.