Определенный интеграл. 1_Опред_Инт_Лек_14. Лекция 14. Определенный интеграл
 Скачать 429.65 Kb. Скачать 429.65 Kb.
|
|
Лекция 14. 6. Определенный интеграл. 6.1. Определение определенного интеграла и его геометрический смысл. Рассмотрим фигуру, ограниченную кривой 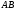 , которая описывается функцией , которая описывается функцией 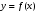 , отрезком , отрезком  по оси по оси 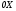 , где , где  и и 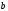 – абсциссы точек – абсциссы точек 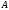 и и 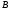 , и прямыми параллельными оси , и прямыми параллельными оси 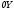 , проведенными из точек A и В. Такая фигура называется криволинейной трапецией. , проведенными из точек A и В. Такая фигура называется криволинейной трапецией.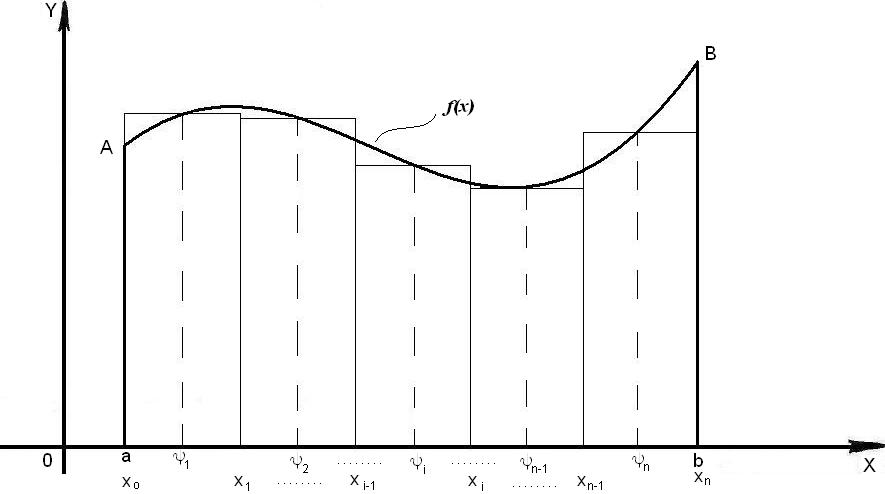 При этом функция 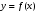 является непрерывной и положительной на отрезке является непрерывной и положительной на отрезке  . Отрезок . Отрезок  называется основанием криволинейной трапеции. называется основанием криволинейной трапеции.Пусть требуется вычислить площадь криволинейной трапеции. Для этого основание  разобьем на разобьем на  более мелких отрезков с помощью более мелких отрезков с помощью 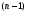 точек. При этом положим точек. При этом положим 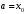 , а , а 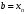 . Через все точки . Через все точки 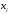 проведем прямые параллельные проведем прямые параллельные 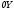 . В результате криволинейная трапеция будет разбита на . В результате криволинейная трапеция будет разбита на  более мелких криволинейных трапеций, и ее площадь будет равна сумме площадей трапеций разбиения: более мелких криволинейных трапеций, и ее площадь будет равна сумме площадей трапеций разбиения:  . .Если заменить каждую из этих трапеций с основанием 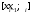 прямоугольником с тем же основанием и высотой прямоугольником с тем же основанием и высотой 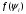 , где , где 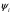 произвольная точка, лежащая внутри каждого основания, то площадь таких прямоугольников приблизительно будет равна площади соответствующих криволинейных трапеций, то есть: произвольная точка, лежащая внутри каждого основания, то площадь таких прямоугольников приблизительно будет равна площади соответствующих криволинейных трапеций, то есть: 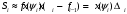 . Тогда площадь всей трапеции приблизительно будет равна: . Тогда площадь всей трапеции приблизительно будет равна: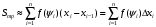 , где , где 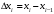 (*). (*).Сумма вида (*) называется интегральной суммой. С увеличением числа таких прямоугольников погрешность в определении площади будет уменьшаться. Поэтому за точное значение площади криволинейной трапеции можно принять предел интегральной суммы при 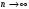 , при условии, что все , при условии, что все 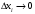 : :  , где , где 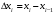 (**). (**).Если предел интегральной суммы равен числу, не зависящему ни от способа разбиения отрезка 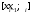 на более мелкие, ни от способа выбора точек на более мелкие, ни от способа выбора точек 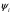 , то это число называется определенным интегралом от функции , то это число называется определенным интегралом от функции 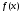 на отрезке на отрезке 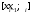 и обозначается так: и обозначается так: 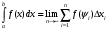 . .Таким образом: Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, когда шаг разбиения стремится к нулю. Числа  и и 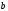 соответственно называются нижней и верхней границами (пределами) интегрирования. соответственно называются нижней и верхней границами (пределами) интегрирования.Отрезок  называется областью интегрирования. называется областью интегрирования.Таким образом, площадь криволинейной трапеции, ограниченной на отрезке  кривой кривой 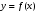 , численно равна определенному интегралу от функции , численно равна определенному интегралу от функции 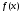 по этому отрезку: по этому отрезку: 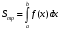 . .В этом заключается геометрический смысл определенного интеграла. Выражение 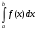 читается так: «Определенный интеграл от читается так: «Определенный интеграл от  до до 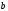 от от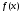 на на 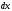 ». ».Замечание 1. Если пределы интегрирования константы, то определенный интеграл является числом. Замечание 2. Определенный интеграл не зависит от обозначения переменной интегрирования: 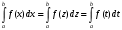 . .Замечание 3. (Теорема существования определенного интеграла). Всякая непрерывная на отрезке  функция интегрируема, то есть для нее существует определенный интеграл. функция интегрируема, то есть для нее существует определенный интеграл.Так же определенный интеграл существует и для ограниченных функций, терпящих на отрезке  конечное число разрывов. конечное число разрывов.6.2. Свойства определенного интеграла. Определенный интеграл обладает следующими свойствами. 1. При перестановке пределов интегрирования местами определенный интеграл меняет свой знак на противоположный: 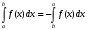 . .Следствие. Определенный интеграл с равными пределами интегрирования равен нулю:  . .2. Постоянный множитель можно выносить за знак определенного интеграла: 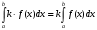 , где , где  - константа. - константа.3. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определенных интегралов от слагаемых: 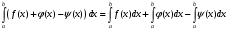 . .4. Если на отрезке интегрирования  подынтегральные функции удовлетворяют неравенству: подынтегральные функции удовлетворяют неравенству: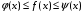 , то этому же неравенству удовлетворяют и определенные интегралы от этих функций: , то этому же неравенству удовлетворяют и определенные интегралы от этих функций:  . .Следствие. Если на отрезке интегрирования  функция функция  ,то и сам интеграл ,то и сам интеграл 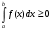 , при этом, если хотя бы в одной точке , при этом, если хотя бы в одной точке 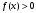 , то и сам интеграл , то и сам интеграл 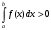 . .Если на отрезке интегрирования  функция функция 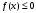 ,то и сам интеграл ,то и сам интеграл 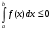 , при этом, если хотя бы в одной точке , при этом, если хотя бы в одной точке 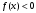 , то и сам интеграл , то и сам интеграл 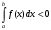 . .5. Если отрезок интегрирования  разбит на несколько частей, например, разбит на несколько частей, например, 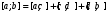 , то определенный интеграл по отрезку , то определенный интеграл по отрезку  равен сумме интегралов по отрезкам разбиения: равен сумме интегралов по отрезкам разбиения: 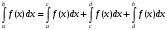 . .6. Если подынтегральная функция 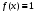 на всем отрезке интегрирования, то значение определенного интеграла дает величину длины отрезка интегрирования на всем отрезке интегрирования, то значение определенного интеграла дает величину длины отрезка интегрирования  . .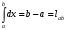 , где , где 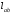 - длина отрезка интегрирования - длина отрезка интегрирования  . .7. Если подынтегральная функция 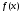 на отрезке интегрирования на отрезке интегрирования  имеет наибольшее имеет наибольшее 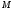 и наименьшее и наименьшее 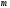 значения, то есть значения, то есть 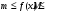 , то справедливо: , то справедливо: 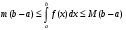 . .Свойство носит название оценочного, так как позволяет приближенно оценить значение определенного интеграла, не прибегая к его вычислению. 8. Определенный интеграл равен произведению значения подынтегральной функции в некоторой точке отрезка интегрирования  на длину этого отрезка: на длину этого отрезка: , где , где 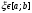 . .Свойство 8 носит название теоремы о среднем, а значение функции 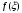 называется ее средним значением на отрезке интегрирования называется ее средним значением на отрезке интегрирования  . .6.3. Формула Ньютона-Лейбница. Способы вычисления определенного интеграла. Почти одновременно двумя математиками Ньютоном и Лейбницем независимо друг от друга была доказана формула, носящая их имя: 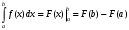 , где , где 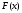 любая первообразная подынтегральной функции. любая первообразная подынтегральной функции.Замечание 1. Формула Ньютона-Лейбница выведена для непрерывной подынтегральной функции. Замечание 2. Нахождение первообразной подынтегральной функции может производиться путем взятия соответствующего неопределенного интеграла. Таким образом, формула Ньютона-Лейбница позволяет вычислять определенный интеграл с помощью неопределенного и использовать все методы, рассмотренные в разделе «Неопределенный интеграл». Замечание 3. При использовании метода подстановки или замены переменной для отыскания первообразной пределы интегрирования пересчитываются для новой переменной. После нахождения первообразной для новой переменной, пересчитанные пределы подставляются в найденную первообразную. Таким образом, обратной замены переменной делать не придется, так как результат будет получен сразу. Замечание 4. Формула метода интегрирования по частям для определенного интеграла выглядит так: 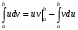 . Пересчитывать пределы в этом случае не надо, так как замены переменной не происходит. . Пересчитывать пределы в этом случае не надо, так как замены переменной не происходит.Пример 1. 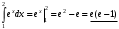 . .Пример 2. 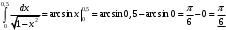 . .Пример 3. 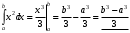 . .Пример 4. 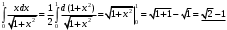 . .Пример 5. 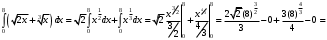 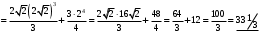 . .Пример 6. 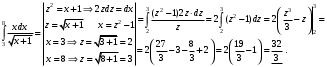 Пример 7. 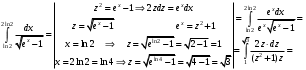 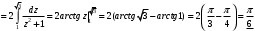 . .Пример 8. 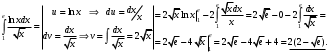 Пример 9. 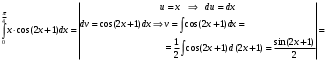 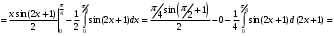 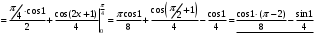 . .6.4. Интегрирование четных и нечетных функций на симметричном отрезке интегрирования. Отрезок интегрирования называется симметричным, если пределы интегрирования равны по модулю, но имеют противоположные знаки: 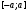 . Рассмотрим интеграл на симметричном отрезке: . Рассмотрим интеграл на симметричном отрезке: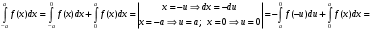 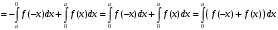 . .Тогда: 1. Если 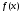 - четная функция, то - четная функция, то 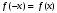 : :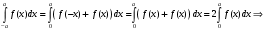 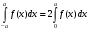 . .Таким образом, определенный интеграл от четной функции на симметричном отрезке равен удвоенному интегралу от этой функции на половинном отрезке. 2. Если 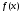 - нечетная функция, то - нечетная функция, то 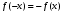 : :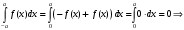 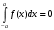 . .Таким образом, определенный интеграл от нечетной функции на симметричном отрезке равен нулю. Замечание.Произведение двух функций, обладающих свойством четности- нечетности, также обладает этим свойством, при этом: - четная х четная = четная - нечетная х нечетная = четная - нечетная х четная = четная х нечетная = нечетная Пример 10. 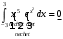 . .Пример 11. 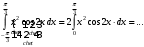 6.5. Несобственные интегралы. 6.5.1. Несобственные интегралы первого рода (c бесконечными пределами интегрирования). Предположим, что область интегрирования является бесконечной, например, правая граница равна бесконечности: 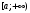 . Тогда, если существует конечный предел . Тогда, если существует конечный предел 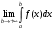 , то он называется несобственным интегралом первого рода и обозначается так: , то он называется несобственным интегралом первого рода и обозначается так: 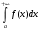 . Таким образом: . Таким образом: 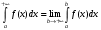 (1). (1).При конечном пределе несобственный интеграл сходится. Если же конечного предела нет, то интеграл расходится. Аналогично определяются интегралы от других бесконечных интервалов: 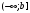 и и 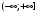 : :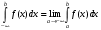 (2). (2).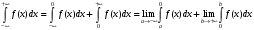 , то есть: , то есть: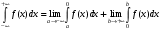 (3). (3).В последнем случае (3) интеграл сходится, если сходятся оба интеграла - слагаемых. Пример 12. 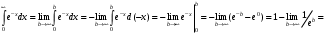 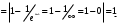 . Интеграл сходится. . Интеграл сходится.Пример 13. 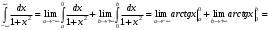 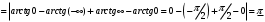 . Интеграл сходится. . Интеграл сходится.Пример 14.  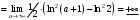 . Интеграл расходится. . Интеграл расходится.6.5.2. Несобственные интегралы второго рода (от разрывных функций). Пусть функция 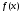 непрерывна на интервале непрерывна на интервале 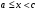 , а в точке , а в точке  терпит разрыв. Тогда, если существует конечный предел терпит разрыв. Тогда, если существует конечный предел 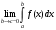 , то он называется несобственным интегралом второго рода: , то он называется несобственным интегралом второго рода:  (4). (4).При конечном пределе несобственный интеграл сходится. Если же конечного предела нет, то интеграл расходится. Если функция терпит разрыв в точке  , то аналогично: , то аналогично: 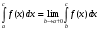 (5). (5).Если функция терпит разрыв в некоторой внутренней точке 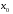 области интегрирования области интегрирования 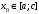 , то: , то: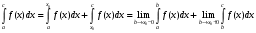 , то есть: , то есть: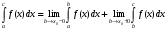 (6). (6).В последнем случае (6) интеграл сходится, если сходятся оба интеграла- слагаемых. Пример 15. 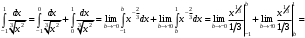 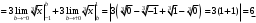 . Интеграл сходится. . Интеграл сходится.6.5.3. Признаки сходимости несобственных интегралов. 1. Если на интервале 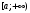 функции функции 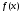 и и 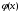 непрерывны и удовлетворяют неравенству непрерывны и удовлетворяют неравенству 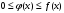 , тогда: , тогда:а) если интеграл 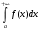 сходится, то интеграл сходится, то интеграл 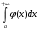 также сходится; то есть, если сходится интеграл от большей функции, то сходится и интеграл от меньшей функции. также сходится; то есть, если сходится интеграл от большей функции, то сходится и интеграл от меньшей функции.б) если интеграл 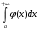 расходится, то интеграл расходится, то интеграл 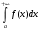 также расходится; то есть, если расходится интеграл от меньшей функции, то расходится и интеграл от большей функции. также расходится; то есть, если расходится интеграл от меньшей функции, то расходится и интеграл от большей функции.2. Если интеграл 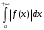 сходится, то интеграл сходится, то интеграл 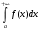 также сходится; то есть, если сходится интеграл от модуля функции, то сходится интеграл и от самой функции. также сходится; то есть, если сходится интеграл от модуля функции, то сходится интеграл и от самой функции.3. Если функции 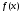 и и 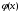 на интервале на интервале 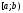 непрерывны и удовлетворяют неравенству непрерывны и удовлетворяют неравенству 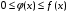 , а в точке , а в точке 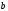 терпят разрыв, тогда: терпят разрыв, тогда:а) если интеграл 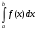 сходится, то интеграл сходится, то интеграл 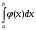 также сходится; то есть, если сходится интеграл от большей функции, то сходится и интеграл от меньшей функции. также сходится; то есть, если сходится интеграл от большей функции, то сходится и интеграл от меньшей функции.б) если интеграл 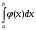 расходится, то интеграл расходится, то интеграл 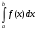 также расходится; то есть, если расходится интеграл от меньшей функции, то расходится и интеграл от большей функции. также расходится; то есть, если расходится интеграл от меньшей функции, то расходится и интеграл от большей функции.4. Если функция 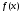 терпит разрыв на отрезке терпит разрыв на отрезке  , а интеграл , а интеграл 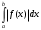 сходится, то интеграл сходится, то интеграл 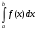 также сходится; то есть, если сходится интеграл от модуля функции, то сходится интеграл и от самой функции. также сходится; то есть, если сходится интеграл от модуля функции, то сходится интеграл и от самой функции.6.6. Задание №14 на практические занятия и самостоятельную работу. Решить самостоятельно на занятии: Б.П.Демидович. «Задачи и упражнения по математическому анализу». В задачнике Демидовича Б.П. есть краткая теория и разобранные примеры. Вычислить определенные интегралы: №1514. 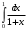 . №1521. . №1521.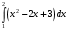 . №1527. . №1527.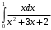 . №1528. . №1528.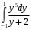 . .№1534.  . №1577. . №1577. , решить заменой , решить заменой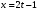 . .№1583. 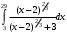 , решить заменой , решить заменой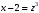 . №1588. . №1588.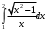 . .№1600. 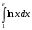 . №1603. . №1603.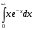 . №1540. . №1540.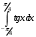 . №1550. . №1550.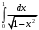 . .№1554. 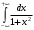 . №1557. . №1557.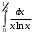 . №1563. . №1563. . .Ответы: №1514. 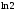 . №1521. . №1521.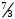 . №1527. . №1527.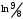 . №1528. . №1528.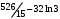 . №1534. . №1534.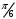 . .№1577. 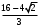 . №1583. . №1583. . №1588. . №1588.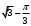 . №1600. . №1600.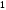 . №1603. . №1603.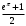 . .№1540. 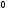 . №1550. . №1550. . №1554. . №1554. . №1557.Расходится. №1563. . №1557.Расходится. №1563.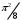 . .Решить дома: Г.Н.Берман. «Сборник задач по курсу математического анализа». № 2231, 2239, 2242, 2251, 2252, 2260, 2264, 2276, 2279; 2328; 2330; 2366, 2369, 2394, 2397. Ответы в конце задачника. |
