Основы теории управлении. Лекция. Лекция 2 Математическое описание автоматической системы управления. Дифференциальное уравнение
 Скачать 143.36 Kb.
|
|
Лекция №2 Математическое описание автоматической системы управления. Дифференциальное уравнение.  Система или устройство x(t)-вход, y(t)- выход. В большинстве случаев при описании используется дифференциальное уравнение. Правая часть содержит производные входа, левая часть производные выхода. m, n – порядок управления, чаще всего так говорят про число n.  Пример 1. 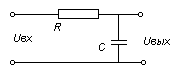     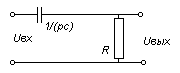 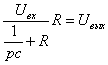 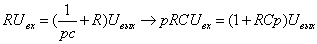Операторное представление. 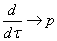    Преобразования Лапласа. 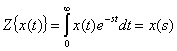   - оригинал. - изображение.Применим преобразования Лапласа к заданному дифференциальному уравнению при нулевых начальных условиях, в результате получим.  s- комплексная переменная x,y-функции от s. Передаточная функция(коэффициент передачи). Отношение изображения выходного сигнала к изображению входного сигала, при нулевых начальных условиях, называется передаточной функцией. Пусть объект описывается уравнением, применим к нему преобразования Лапласа.    - передаточная функция.Пример:   Найти коэффициент передачи. 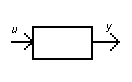  Моделирование динамических объектов(систем). 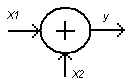   найти решение -->  Утверждение: Системы уравнений могут быть смоделированы при помощи трех функциональных блоков.  -сумматор -усилитель –интеграторПример:  Смоделировать устройство которое описывается этим уравнением. Переходим к изображению     Принципиальная схема: 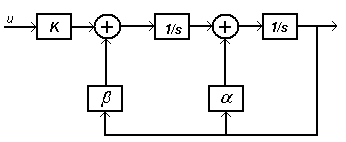 Лекция №3 Характеристики динамических систем: Временные. Частотные. 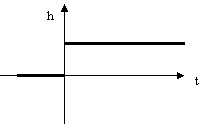 Временное устройство U(t)=1 или u(t)=1(t) – на вход подается единичный сигнал. выходной сигнал h(t) – переходной функцией называется реакция на единичную ступень. Если перейти к изображению. y(s)=w(s)u(s)  s-комплексная переменная.  - изображение переходной функции равно изображению передаточной функции деленное на s.Импульсная переходная функция(весовая функция). Называется реакция системы на импульс. 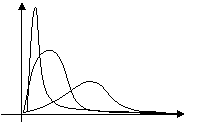 - реакция системы на импульс. - дельта импульс.   Основная характеристика дельта импульса: 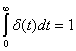 высота дельта импульса стремиться к  ширина дельта импульса стремиться к 0 S=1 Рассмотрим связь между двумя временными характеристиками и их изображением. 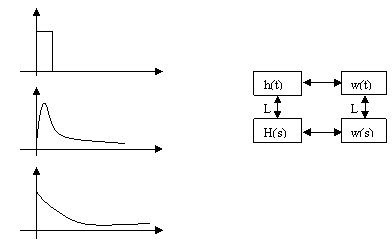 Пример: Апериодическое звено. 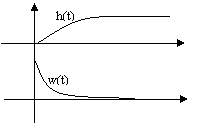  - связь между изображением переходной функции и изображением импульсной переходной функцией.Интеграл от импульсной переходной функции есть переходная функция. Реальное дифференцирующее звено. 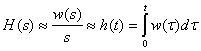 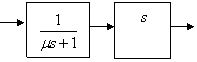 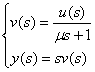      Лекция №4 При исследовании и создании САУ, аппарат частотных характеристик был одним из первых, т.к они наиболее полно отражают физическую природу процессов, происходящих в динамических объектах. В качестве преобразования функции f(t) используется преобразование Фурье  Преобразование Фурье позволяет разложить непериодическую функцию f(t) для которой выполняется условие сходимости  в бесконечный ряд гармоник, образующих непрерывный спектр частот в интервале  от до с бесконечно малым интервалом частот между смежными частотами ( 0).Отметим, что по сравнению с преобразованием Лапласа преобразование Фурье позволяет отобразить оригинал только на мнимую ось, в преобразовании Лапласа же используется вся комплексная плоскость. Для перехода к частотным характеристикам, необходимо в уравнение ПФ (3) вместо оператора Лапласа p подставить оператор Фурье  , получим частотную характеристику
Рассмотрим понятие о частотных характеристиках. Если на вход линейной разомкнутой системы (или звена) подать гармонический входной сигнал, то по истечении некоторого времени окончания переходных процессов на выходе системы (звена) установится также гармонический выходной сигнал той же частоты. Амплитуда и фаза при прочих равных условиях будут зависеть от частоты входного сигнала. По ним, как будет показано дальше, можно судить о свойствах САУ. Достоинством частотных методов является то, что частотные характеристики можно снять экспериментально. Чтобы снять частотную характеристику необходимо на вход подавать гармонический сигнал, изменяя частоту от 0 до , а на выходе измерять амплитуду и фазу для частот wi,.Отметим еще, что в выражении передаточной функции и частотной характеристики для реальных систем степень знаменателя всегда больше степени числителя n>m, т.к. полоса пропускания частот реальной системы всегда ограничена. Действительно, если n Частотная характеристика (ЧХ) элемента или системы  может быть представлена в двух видах:   - вещественно-частотная характеристика (ВЧХ); - мнимо-частотная характеристика (МЧХ); - амплитудно-частотная характеристика (АЧХ); - фазо-частотная характеристика (ФЧХ).Часто ЧХ представляется графически (рис.1) на комплексной плоскости, где все указанные величины связаны между собой по следующим соотношениям. 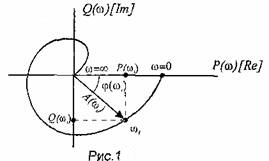   Часто при исследовании систем используются логарифмические частотные характеристики. Понятие о логарифмических частотных характеристиках При исследовании САУ, амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это связано с двумя обстоятельствами: в логарифмических масштабах кривизна характеристик резко уменьшается, что позволяет в большинстве практических случаев приближенно изображать АЧХ ломаными линиями в логарифмических масштабах АЧХ цепочки звеньев равна сумме АЧХ отдельных звеньев  АЧХ в логарифмических масштабах строится в координатах  и а ФЧХ - в виде зависимости от . Единицей измерения  служит децибел, равная 0,1 бела. Бел - единица измерения десятичного логарифма коэффициента усиления мощности сигнала, т.е. 1 бел соответствует усилению мощности в 10 раз, 2 бела - в 100 раз и т.д. Так как мощность сигнала пропорциональна квадрату амплитуды А2(Пример: для электрической цепи 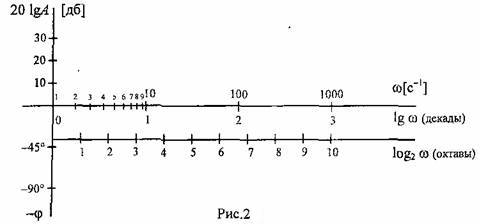 ). , то усиление в белах, выраженное через отношение амплитуд A, равно  , соответственно в децибелах оно равно  По оси абсцисс откладывается в логарифмическом масштабе частот  (десятичный логарифм)(изменение частоты в 10 раз - декада), а около отметок указывается само значение частоты. Иногда По оси абсцисс откладывается в логарифмическом масштабе частота (десятичный логарифм) (изменение частоты в 10 раз - декада), а около отметок указывается само значение частоты. Иногда применяется логарифм частоты при основании 2 (изменение частоты в два раза - октава) одна октава разно 0,303 декады, т.к. lg2 = 0,303 .Для построения логарифмических фазовых характеристик (ЛФХ) на оси абсцисс используется аналогичная шкала частот  или  , а по оси ординат (обычно используется нижняя часть плоскости) откладывается фаза в градусах.Отметим ещё, т.к. точка  =0 в логарифмическом масштабе находится слева , то ЛАФХ строятся не от =0, а от достаточно малого, но конечного значения , которое и откладывается в начале координат |
