Лекция 23 модели статистического прогнозирования план о статистике и статистических данных

• Название: Лекция 23 модели статистического прогнозирования план о статистике и статистических данных
• Дата: 27.11.2022
• Размер: 3.22 Mb.
• Имя файла: lektsiya--23-modeli-statisticheskogo-prognozirovaniya.docx
• Тип: Лекция; #815452

Лекция № 23 МОДЕЛИ СТАТИСТИЧЕСКОГО ПРОГНОЗИРОВАНИЯ
ПЛАН

1. 
   О статистике и статистических данных.
   
2. 
   Метод наименьших квадратов.
   
3. 
   Прогнозирование по регрессионной модели.
   

1 О статистике и статистических данных
Рассмотрим способ нахождения зависимости частоты заболе­ваемости жителей города бронхиальной астмой от качества возду­ ха (третий пример из сформулированных в начале предыдущего параграфа). Любому человеку понятно, что такая зависимость су­ществует. Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное заключение. Его недостаточно для того, чтобы управлять уровнем загрязненности воздуха. Для управления требуются более конкретные знания. Нужно устано­вить, какие именно примеси сильнее всего влияют на здоровье людей, как связана концентрация этих примесей в воздухе с чис­лом заболеваний. Такую зависимость можно установить только экспериментальным путем: посредством сбора многочисленных данных, их анализа и обобщения.

При решении таких проблем на помощь приходит статистика.

Статистика - наука о сборе, измерении и анализе массовых количественных данных.

Существуют медицинская статистика, экономическая статис­тика, социальная статистика и другие. Математический аппарат статистики разрабатывает наука под названием математическая статистика.

Рассмотрим пример из области медицинской статистики.

Известно, что наиболее сильное влияние на бронхиально-легоч­ные заболевания оказывает угарный газ - монооксид углерода. Поставив цель определить эту зависимость, специалисты по меди­цинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмос­фере и о заболеваемости астмой (число хронических больных на 1000 жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы (рис .3.3¹ ) .

¹ Приведенные в примере данные не являются официальной статисти­кой, однако правдоподобны.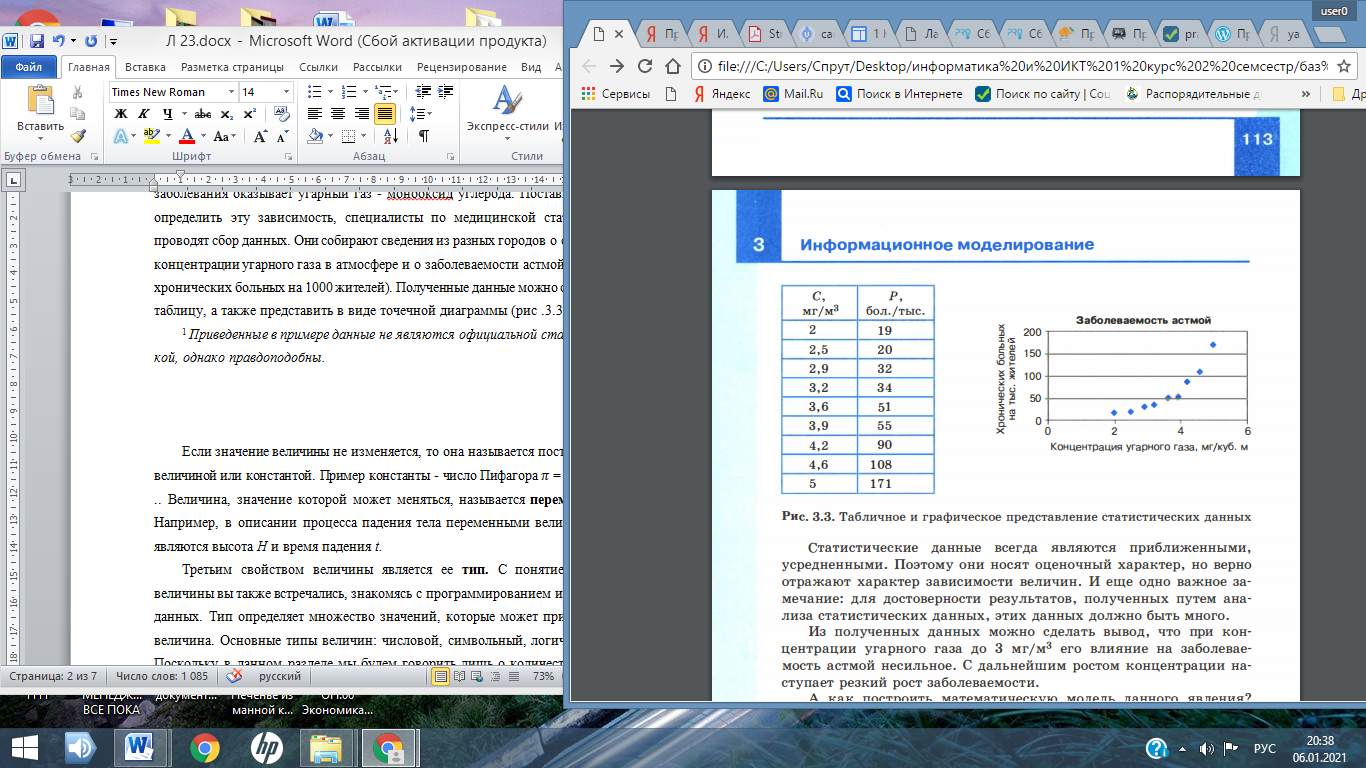



Рис. 3.3. Табличное и графическое представление статистических данных
Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер, но верно отражают характер зависимости величин. И еще одно важное за­мечание: для достоверности результатов, полученных путем ана­лиза статистических данных, этих данных должно быть много.

Из полученных данных можно сделать вывод, что при кон­центрации угарного газа до 3 мг /м³ его влияние на заболевае­мость астмой несильное. С дальнейшим ростом концентрации на­ ступает резкий рост заболеваемости.

А как построить математическую модель данного явления? Очевидно, нужно получить формулу, отражающую зависимость количества хронических больных Р от концентрации угарного газа С. На языке математики это называется функцией зависи­мости Р от С: Р(С). Вид такой функции неизвестен, ее следует искать методом подбора по экспериментальным данным.

Понятно, что график искомой функции должен проходить близко к точкам диаграммы экспериментальных данных. Строить функцию так, чтобы ее график точно проходил через все данные точки (рис.3.4,а), не имеет смысла. Во-первых, математический вид такой функции может оказаться слишком сложным. Во-вто­рых, уже говорилось о том, что экспериментальные значения яв­ляются приближенными. Отсюда следуют основные требования к искомой функции:

• она должна быть достаточно простой для использования ее в дальнейших вычислениях;

• график этой функции должен проходить вблизи экспери­ментальных точек так, чтобы отклонения этих точек от гра­фика были минимальны и равномерны (рис.3.4,6).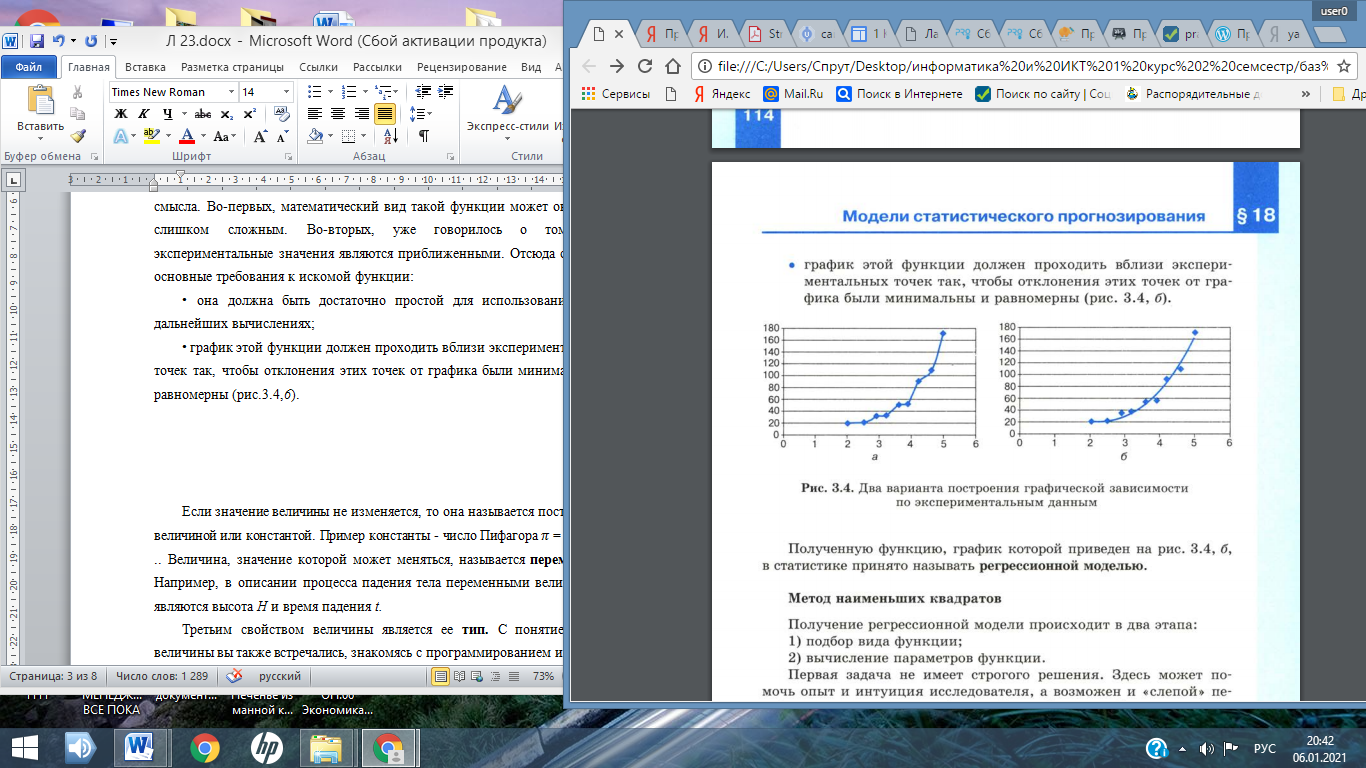



Рис. 3.4. Два варианта построения графической зависимости по экспериментальным данным
Полученную функцию, график которой приведен на рис.3.4,б, в статистике принято называть регрессионной моделью.

2 Метод наименьших квадратов
Получение регрессионной модели происходит в два этапа:

1) подбор вида функции;

2) вычисление параметров функции.

Первая задача не имеет строгого решения. Здесь может по­мочь опыт и интуиция исследователя, а возможен и «слепой» пе­ребор из конечного числа функций и выбор лучшей из них.

Чаще всего выбор производится среди следующих функций:

у = ах + b - линейная функция;

у = ах² + bх + с - квадратичная функция;

у = а ln (x) + b - логарифмическая функция;

у = а е ^bх - экспоненциальная функция;

у = ах^b - степенная функция.

Квадратичная функция называется в математике полиномом второй степени. Иногда используются полиномы и более высо­ких степеней, например полином третьей степени имеет вид: у= ах3 + bх² + сх + d.

Во всех этих формулах:

х - аргумент,

у - значение функции,

а, b, с, d - параметры функции,

ln(x) - натуральный логарифм,

е - константа, основание натурального логарифма.

Если вы выбрали (сознательно или наугад) одну из предлагае­мых функций, то далее нужно подобрать параметры (а, b, с и пр.) так, чтобы функция располагалась как можно ближе к экспери­ментальным точкам. Что значит «располагалась как можно бли­же»? Ответить на этот вопрос значит предложить метод вычис­ления параметров. Такой метод был предложен в XVIII веке немецким математиком К. Гауссом и называется методом наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квад­ратов отклонений у-координат всех экспериментальных точек от у-координат графика функции была минимальной.

Мы не будем здесь производить подробное математическое описание метода наименьших квадратов. Достаточно того, что вы теперь знаете о существовании такого метода. Он очень широко используется в статистической обработке данных и встроен во многие математические пакеты программ. Важно понимать следу­ющее: методом наименьших квадратов по данному набору экспе­риментальных точек можно построить любую (в том числе и из рассмотренных выше) функцию. А вот будет ли она нас удовлет­ворять, это уже другой вопрос - вопрос критерия соответствия. На рис.3.5 изображены три функции, построенные методом наи­меньших квадратов по приведенным экспериментальным данным.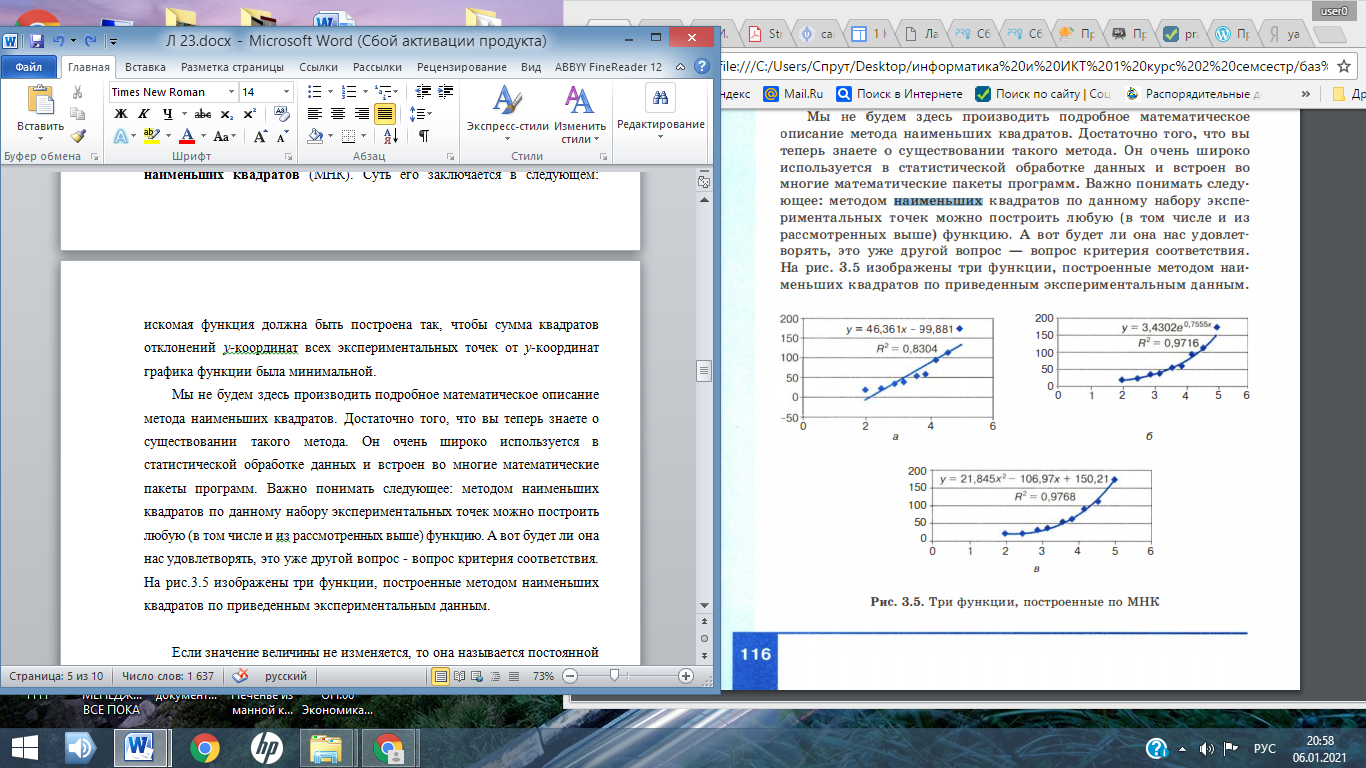


Рис. 3.5. Три функции, построенные по МНК
Эти рисунки получены с помощью табличного процессора Microsoft Excel . График регрессионной модели называется трен­ дом. Английское слово trend можно перевести как « общее на­ правление » или « тенденция») .

Уже с первого взгляда хочется отбраковать вариант линейного тренда. График линейной функции - это прямая. Полученная по МНК прямая отражает факт роста заболеваемости от концентра­ции угарного газа, но по этому графику трудно что-либо сказать о характере этого роста. А вот квадратичный и экспоненциальный тренды правдоподобны. Теперь пора обратить внимание на надпи­си, присутствующие на графиках. Во-первых, это записанные в явном виде искомые функции - регрессионные модели:

линейная функция: у = 46,361х - 99,881;

экспоненциальная функция: у = 3,4302 е ^0,7555х;

квадратичная функция: у = 21,845х² - 106,97х + 150,21.

На графиках присутствует еще одна величина, полученная в результате построения трендов. Она обозначена как R². В статис­тике эта величина называется коэффициентом детерминирован­ности. Именно она определяет, насколько удачной является по­ лученная регрессионная модель. Коэффициент детерминирован­ности всегда заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если О, то выбранный вид регрессионной модели предельно неудачен. Чем R² ближе к 1, тем удачнее регрессионная модель.

Из трех выбранных моделей значение R² наименьшее у линей­ной. Значит, она самая неудачная (нам и так это было понятно). Значения же R2 у двух других моделей достаточно близки (разни­ца меньше 0,01). Если определить погрешность решения данной задачи как 0,01, по критерию R² эти модели нельзя разделить. Они одинаково удачны. Здесь могут вступить в силу качествен­ные соображения. Например, если считать, что наиболее сущест­венно влияние концентрации угарного газа проявляется при боль­ших величинах, то, глядя на графики, предпочтение следует от­дать квадратичной модели. Она лучше отражает резкий рост заболеваемости при больших концентрациях примеси.

Интересный факт: опыт показывает, что если человеку пред­ложить на данной точечной диаграмме провести «на глаз» пря­мую так, чтобы точки были равномерно разбросаны вокруг нее, то он проведет линию, достаточно близкую к той, что дает МНК.
3 Прогнозирование по регрессионной модели
Мы получили регрессионную математическую модель и мо­жем прогнозировать процесс путем вычислений. Теперь можно оценить уровень заболеваемости астмой не только для тех значе­ний концентрации угарного газа, которые были получены путем измерений, но и для других значений. Это очень важно с практи­ческой точки зрения. Например, если в городе планируется по­строить завод, который будет выбрасывать в атмосферу угарный газ, то, рассчитав его возможную концентрацию, можно предсказать, как это отразится на заболеваемости астмой жителей города.

Существует два способа прогнозирования по регрессионной модели. Если прогноз производится в пределах эксперименталь­ных значений независимой переменной (в нашем случае это кон­центрация угарного газа С), то это называется восстановлением значения.

Прогнозирование за пределами экспериментальных данных называется экстраполяцией.

Имея регрессионную модель, легко прогнозировать, производя расчеты с помощью электронных таблиц. Выберем для нашего примера в качестве наиболее подходящей квадратичную зависи­мость. Построим следующую электронную таблицу: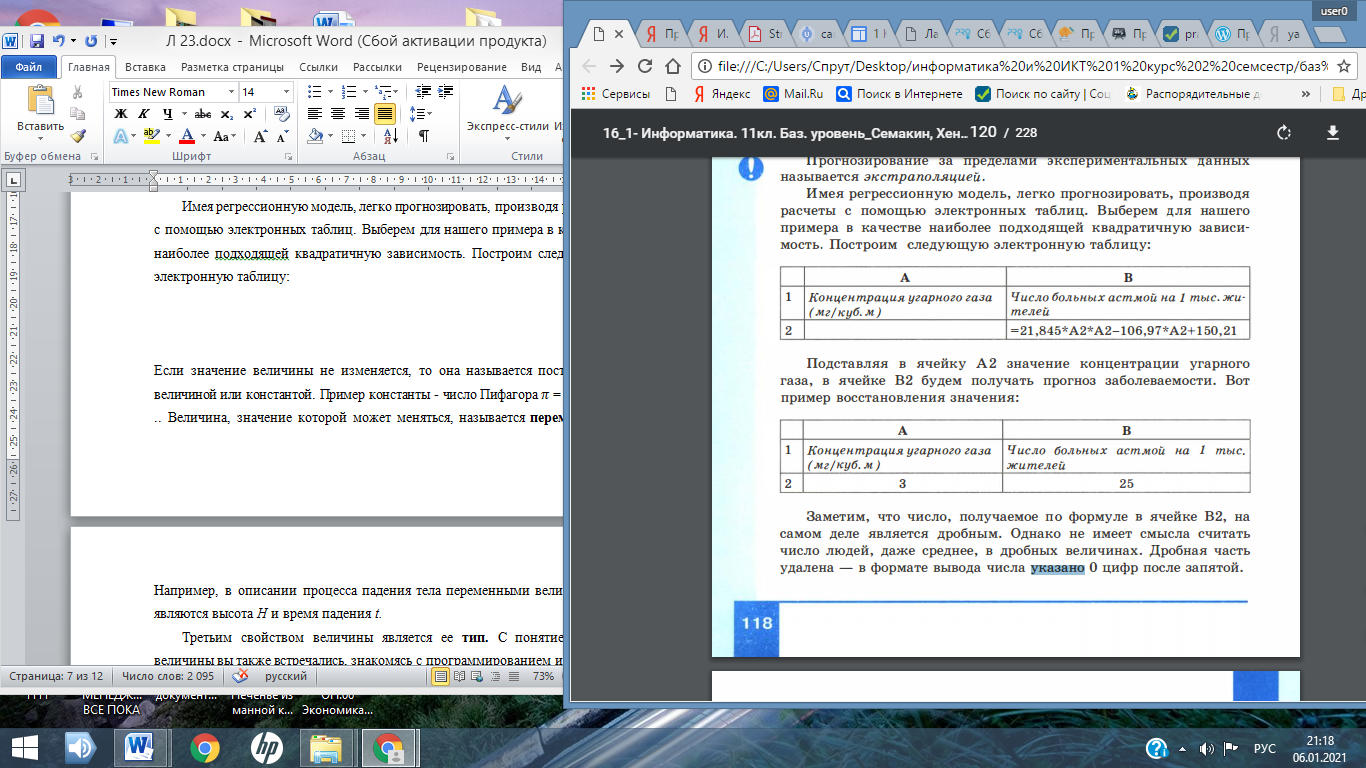



Подставляя в ячейку А2 значение концентрации угарного газа, в ячейке В2 будем получать прогноз заболеваемости. Вот пример восстановления значения:



Заметим, что число, получаемое по формуле в ячейке В2, на самом деле является дробным. Однако не имеет смысла считать число людей, даже среднее, в дробных величинах. Дробная часть удалена - в формате вывода числа указано 0 цифр после запятой.

Экстраполяционный прогноз выполняется аналогично.

Табличный процессор дает возможность производить экстра­поляцию графическим способом, продолжая тренд за пределы экспериментальных данных. Как это выглядит при использова­нии квадратичного тренда для

С= 7, показано на рис . 3.6.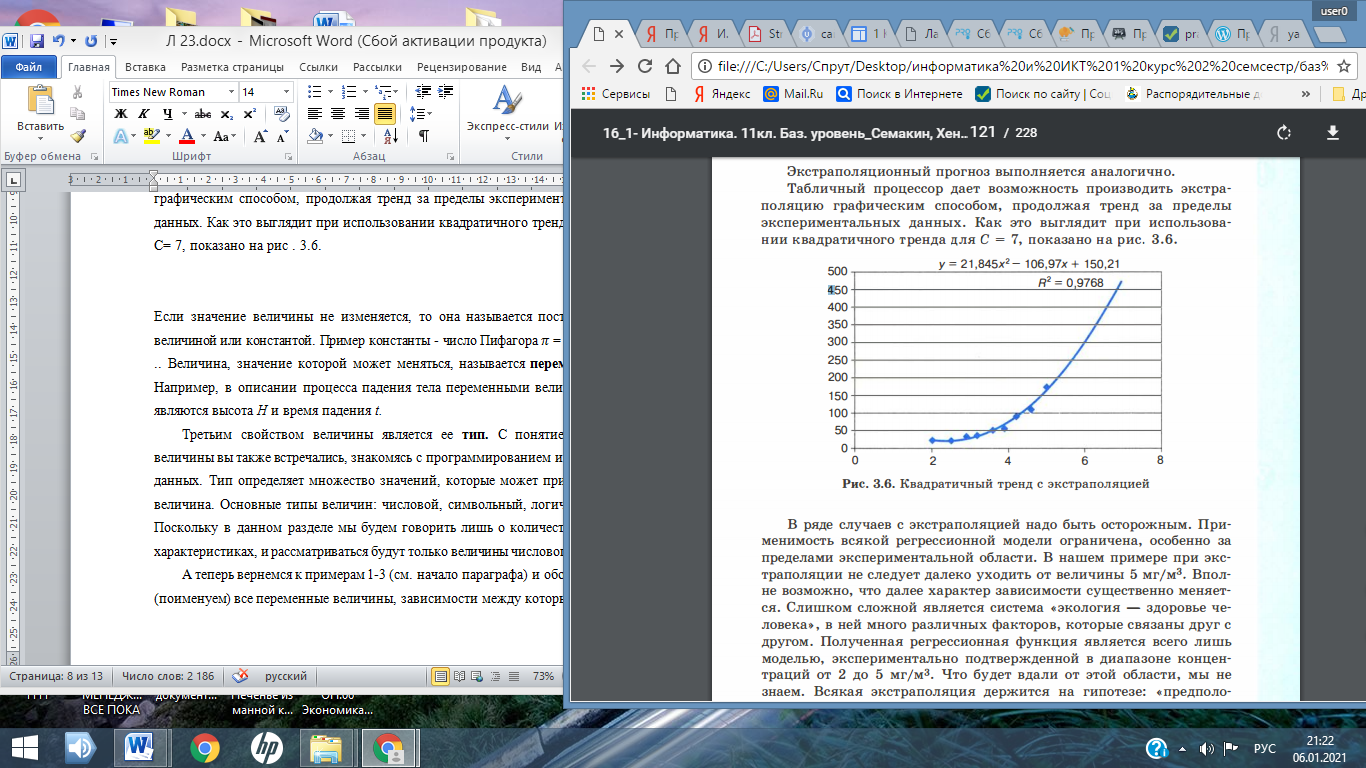



Рис. 3.6. Квадратичный тренд с экстраполяцией
В ряде случаев с экстраполяцией надо быть осторожным. Применимость всякой регрессионной модели ограничена, особенно за пределами экспериментальной области. В нашем примере при экс­траполяции не следует далеко уходить от величины 5 мг/м³. Впол­не возможно, что далее характер зависимости существенно меняет­ся. Слишком сложной является система « экология - здоровье че­ловека», в ней много различных факторов, которые связаны друг с другом. Полученная регрессионная функция является всего лишь моделью, экспериментально подтвержденной в диапазоне концентраций от 2 до 5 мг/м³ . Что будет вдали от этой области, мы не знаем. Всякая экстраполяция держится на гипотезе: «предполо­жим, что за пределами экспериментальной области закономерность сохраняется». А если не сохраняется?

Квадратичная модель в данном примере в области малых зна­чений концентрации, близких к 0, вообще не годится. Экстрапо­лируя ее на С= 0 мг/м³, получим 150 человек больных, т. е. боль­ше, чем при 4 мг /м³. Очевидно, это нелепость. В области малых значений С лучше работает экспоненциальная модель. Кстати, это довольно типичная ситуация: разным областям данных могут лучше соответствовать разные модел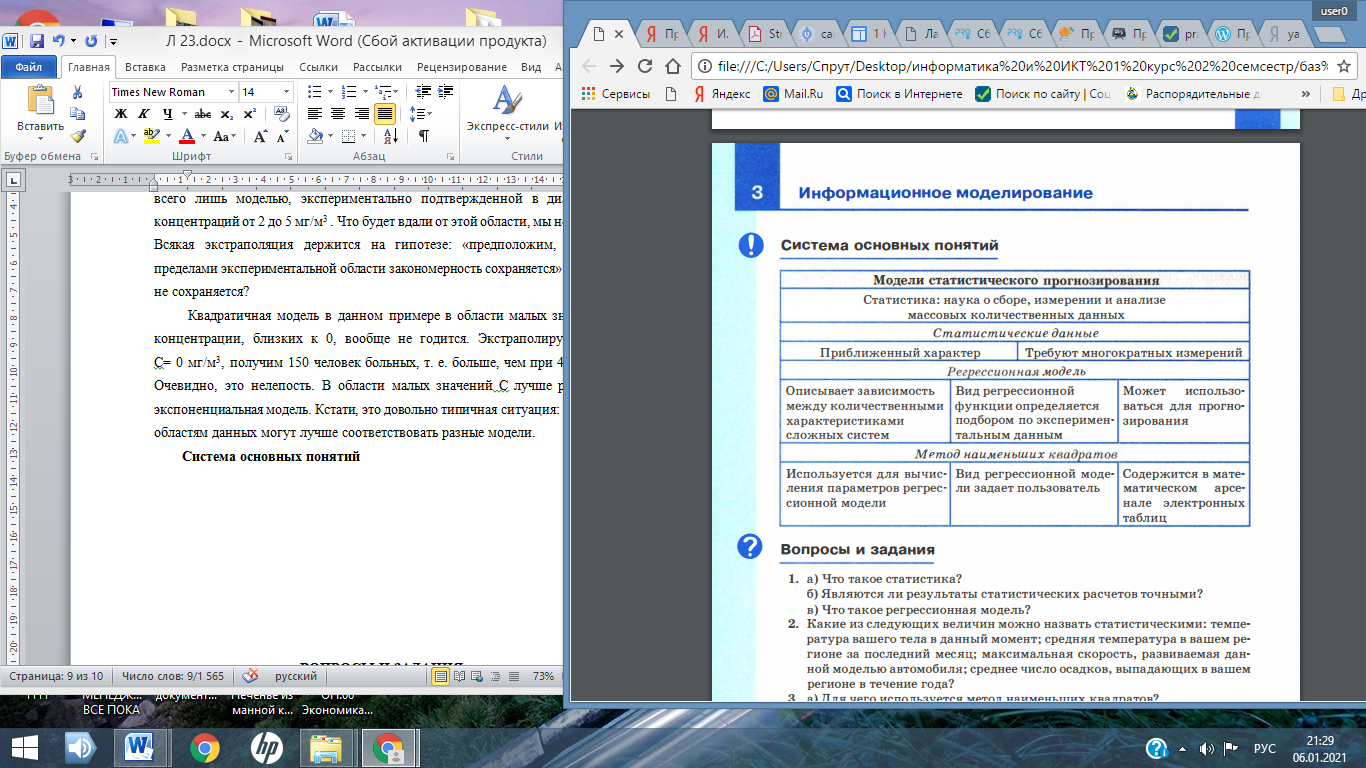и.

Система основных понятий





ВОПРОСЫ И ЗАДАНИЯ
1. а) Что такое статистика?

б) Являются ли результаты статистических расчетов точными?

в) Что такое регрессионная модель?

2. Какие из следующих величин можно назвать статистическими: температура вашего тела в данный момент; средняя температура в вашем регионе за последний месяц; максимальная скорость, развиваемая дан­ ной моделью автомобиля; среднее число осадков, выпадающих в вашем регионе в течение года?

3. а) Для чего используется метод наименьших квадратов?

б) Что такое тренд?

в) Как располагается линия тренда, построенная по МНК, относительно экспериментальных точек?

г) Может ли тренд, построенный по МНК, пройти выше всех экспериментальных точек?

4. а) В чем смысл параметра R ² ? Какие значения он принимает?

б) Какое значение примет параметр R ² , если тренд точно проходит через экспериментальные точки?

5. По данным из следующей таблицы постройте с помощью Excel линей­ную, квадратичную, экспоненциальную и логарифмическую регресси­онные модели. Определите параметры, выберите лучшую модель.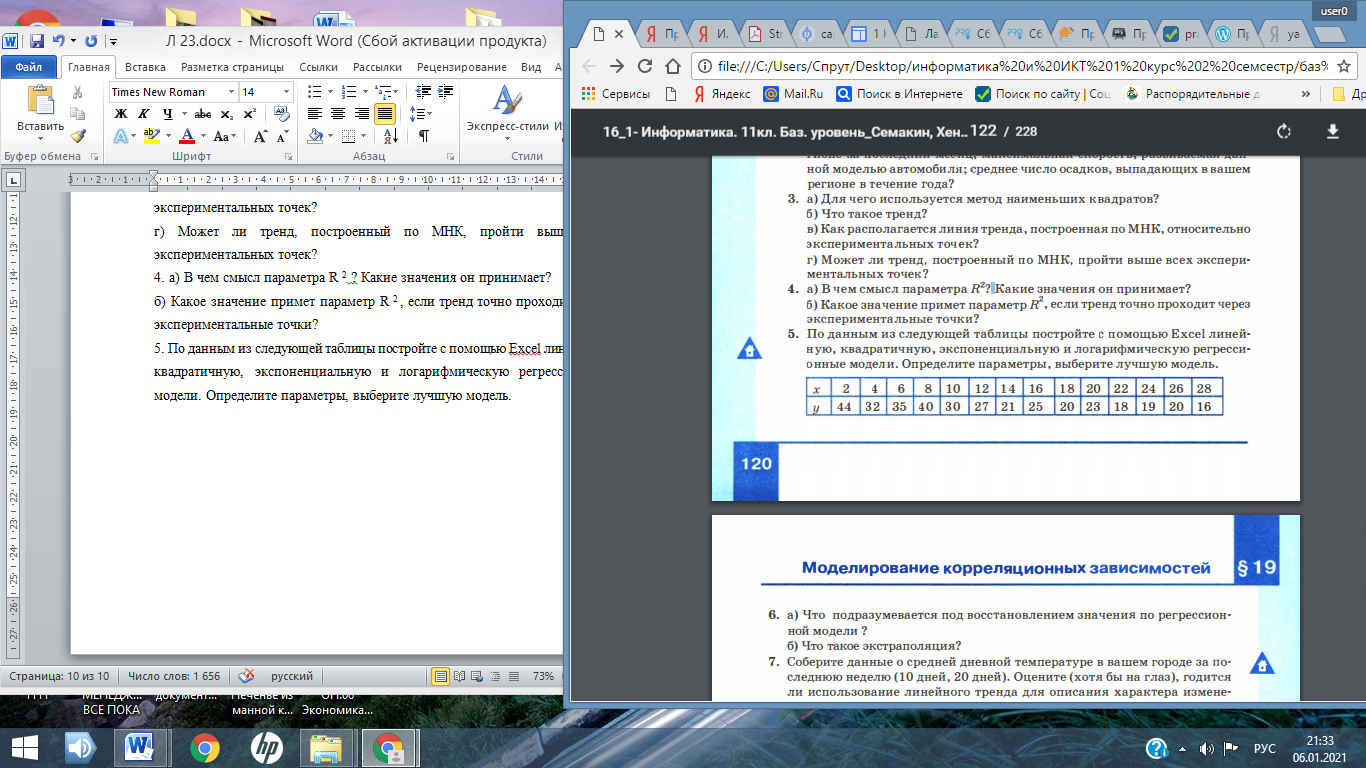



6. а) Что подразумевается под восстановлением значения по регрессион­ной модели?

б) Что такое экстраполяция?

7. Соберите данные о средней дневной температуре в вашем городе за последнюю неделю (10 дней, 20 дней). Оцените (хотя бы на глаз), годится ли использование линейного тренда для описания характера измене­ния температуры со временем. Попробуйте путем графической экстра­поляции предсказать температуру через 2-5 дней.

8. Придумайте свои примеры практических задач, для которых имело бы смысл выполнение восстановления значений и экстраполяционных расчетов.

Скачано с www.znanio.ru