Лекция25 (Элементы теории поля). Лекция 25 25. Элементы теории поля 25 Основные понятия
 Скачать 99 Kb. Скачать 99 Kb.
|
|
Лекция 25 25. Элементы теории поля 25.1. Основные понятия Определение. Говорят, что в некоторой области D трехмерного пространства задано скалярное поле, если каждой точке MD поставлено в соответствие число. Зададим прямоугольную декартову систему координат Oxyz. Тогда скалярное поле задает некоторую функцию U=U(x,y,z). Для наглядного геометрического изображения скалярного поля используют поверхности уровня. Поверхность уровня - это множество точек области D, для которой функция принимает постоянное значение U(x,y,z)=C, где C=const. Примеры. Поле распределения температур в неравномерно разогретом теле, поле распределения масс внутри тела. Определение. Говорят, что в некоторой области D трехмерного пространства задано векторное поле, если каждой точке MD поставлен в соответствие вектор F. Зададим прямоугольную декартову систему координат Oxyz. Обозначим единичные векторы осей Ox,Oy и Oz буквами i,j,k. Тогда в области D векторное поле F задает тройку функций: F =P(x,y,z) i+Q(x,y,z) j+R(x,y,z) k = (P(x,y,z); Q(x,y,z);R(x,y,z)). Примеры. Поле распределения скоростей частиц жидкости в области D. Поле распределения напряженностей электростатического поля. Пусть задано некоторое скалярное поле U=U(x,y,z) и пусть функция U непрерывна и непрерывно дифференцируема. Определение. Градиентом функции U называется вектор, равный Вектор градиент в каждой точке перпендикулярен поверхности уровня поля U и показывает направление быстрейшего возрастания функции U. Пусть l - единичный вектор. Производная по направлению равна Пусть задано некоторое векторное поле F = (P(x,y,z); Q(x,y,z);R(x,y,z)) и пусть функция P,Q,R непрерывное и непрерывно дифференцируемое. Определение. Дивиргенцией векторного поля F называется величина, равная Для случая поля течения жидкостей дивиргенция F показывает мощность источников жидкости в данной точке поля. Определение. Вихрем или ротором векторного поля F называется вектор, равный Ротор F показывает величину завихренности поля. Определение. Векторное поле F называется потенциальным в области D, если существует функция U=U(x,y,z) такая, что F= gradU. Функция U называется потенциальной функцией поля. Пример. Поле распределения напряженностей электростатического поля. Потенциальная функция равна где - потенциал электростатического поля. Напряженность поля равна Определение. Векторное поле F называется соленоидальным в области D, если существует векторное поле A такое, что F= rot A. Векторное поле A называется векторным потенциалом поля. Пример. Поле распределения напряженностей магнитостатического поля. Введем обозначение r=(x,y,z)=x i + y j+ z k. Тогда dr=(dx,dy,dz)= i dx + j dy + k dz. Определение. Пусть задано некоторое векторное поле F в области D. Зададим некоторый контур L, лежащий в области D. Если F - силовое поле. то интеграл по контуру определяет работу силового поля при перемещении тела по контуру L. Если контур L замкнут, то интеграл называется циркуляцией. Определение. Пусть задано некоторое векторное поле F в области D. Зададим некоторую двустороннюю поверхность, лежащую в области D. Потоком векторного поля через поверхность называется величина Для случая поля течения жидкостей поток векторного поля F равен количеству жидкости, протекающей через данную поверхность. 25.2. Оператор Гамильтона Для упрощения работы с введенными понятиями Гамильтон ввел символический оператор , равный Оператор называется набла. С помощью введенного оператора запишем 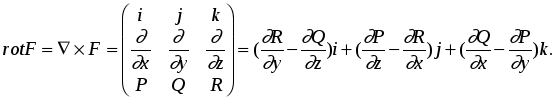 Теорема. Для того чтобы поле F было потенциальным, необходимо и достаточно, чтобы rot F=0. Доказательство. Необходимость. Пусть поле потенциально. Это значит, что существует потенциал U=U(x,y,z) такой, что F= gradU. Тогда 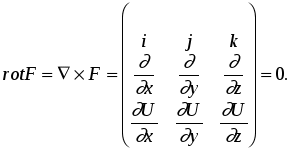 Достаточность. Пусть rot F=0. Тогда Это значит интеграл по контуру в области не зависит от вида контура, а зависит только от начала M0(x0,y0,z0) и конца M(x,y,z) контура. Поэтому запишем 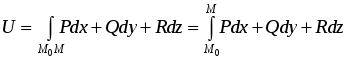 Найдем производную. Получим Это значит, что Теорема Остроградского-Гаусса и теорема Стокса являются наиболее используемыми теоремами теории поля. Поэтому сформулируем их еще раз в новых терминах Теорема Остроградского-Гаусса. Пусть в некоторой области D трехмерного пространства задано векторное поле F. F =P(x,y,z) i+Q(x,y,z) j+R(x,y,z) k = (P(x,y,z); Q(x,y,z);R(x,y,z)). пусть S - замкнутая поверхность, лежащая в области D, V - тело, ограниченное поверхностью S. Если функции непрерывны и имеют непрерывные частные производные, то поток векторного поля через поверхность S равен интегралу по объему от дивиргенции F Интеграл берется по внешней стороне поверхности. Разделим обе части равенства на V и перейдем к пределу при V 0. Получим 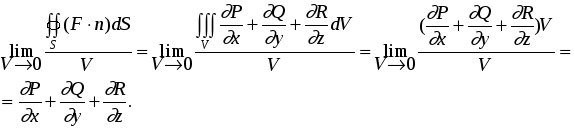 Для случая поля скоростей течения жидкости поток равен количеству жидкости, протекающей через поверхность S. Если он равен нулю, то количество втекающей жидкости равно количеству вытекающей. Если поток равен нулю для любого объема, то жидкость внутри объема не появляется и не исчезает. Это соответствует случаю дивергенции, равному нулю. Если поток через замкнутую поверхность больше нуля, то это означает, что внутри поверхности имеется источник жидкости. Поэтому дивергенция характеризует мощность источников жидкости в данной точке поля. Теорема Стокса. Пусть в некоторой области D трехмерного пространства задано векторное поле F. F =P(x,y,z) i+Q(x,y,z) j+R(x,y,z) k = (P(x,y,z); Q(x,y,z);R(x,y,z)). Пусть L замкнутый контур, лежащий в области D, S - некоторая поверхность, натянутая на контур L. Поверхность S лежит в области D. Направление обхода контура и выбор стороны поверхности согласованы по следующему правилу: если двигаться по направлению обхода контура так, чтобы поверхность оставалась с левой стороны, то нормаль к поверхности проходит от ног к голове. Если функции непрерывны и имеют в области D непрерывные частные производные, то циркуляция по контуру равна потоку ротора через поверхность S Разделим обе части равенства на S и перейдем к пределу при S 0. Получим 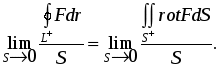 Из теоремы Стокса следует, что 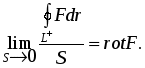 Ротор F показывает величину завихренности поля. |
