Лекция 3 ОИиПО. Лекция 3. Понятие блоксхемы. Основные элементы блоксхем
 Скачать 272.91 Kb. Скачать 272.91 Kb.
|
|
Лекция №3. Понятие блок-схемы. Основные элементы блок-схем. Понятие алгоритма является одним из основных понятий вычислительной математики и информатики. Алгоритм — строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов. Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя. Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.  В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные. Наглядным и удобным способом изображения алгоритмов для исполнителя-человека являются блок-схемы. Блок-схема — это схематичное представление процесса, системы или компьютерного алгоритма. Блок-схемы часто применяются в разных сферах деятельности, чтобы документировать, изучать, планировать, совершенствовать и объяснять сложные процессы с помощью простых логичных диаграмм. Для построения блок-схем применяются прямоугольники, овалы, ромбы и некоторые другие фигуры (для обозначения конкретных операций), а также соединительные стрелки, которые указывают последовательность шагов или направление процесса. Блок-схемы варьируются от незамысловатых, нарисованных вручную до подробных, составленных на компьютере диаграмм с множеством шагов и процессов. Если учесть все возможные вариации, блок-схемы можно признать одним из самых распространенных видов схем во всем мире. Они широко используются в разных сферах как технической, так и нетехнической направленности. Блок-схема алгоритма – это его графическое изображение в виде схемы связанных между собой с помощью линий перехода блоков – специальных графических объектов, каждый из которых соответствует определенным шагам алгоритма. Блок–схема — это ориентированный граф, указывающий порядок выполнения команд в алгоритме, по сути, это графический способ записи алгоритма. Внутри блока дается описание соответствующих действий. Блоки, как правило, располагаются сверху вниз. Линии соединения отдельных блоков показывают направление процесса обработки в схеме. Стрелки на соединяющих линиях не ставятся при направлениях сверху вниз и слева направо; противоположные направления показывают стрелкой на линии. Вершинами графа являются геометрические фигуры, внутри которых записывается указание (команда) алгоритма или помечается его начало и конец, как правило, в блок – схемах используют следующие фигуры – Рис.1. 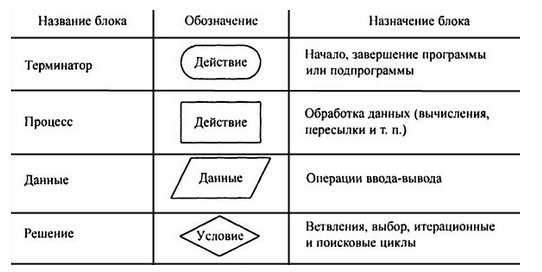 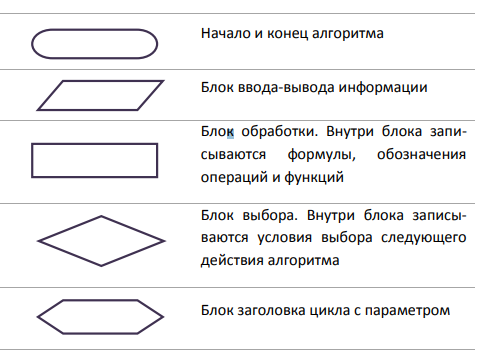  Рис. 1. Фигуры блок-схем В блок-схемах используется двойной символ « := », который обозначает команду «присвоить значение». Существуют три основные разновидности алгоритмических действий, сочетанием которых можно описать любой алгоритм: линейная последовательность (следование), выбор (разветвление), повторение (цикл). Линейная последовательность (следование) – это набор действий, выполняемых последовательно друг за другом. На блок-схеме ему соответствует несколько расположенных друг за другом блоков обработки и/или блоков ввода-вывода (рис. 2). 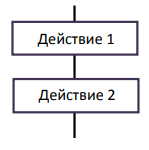 Рис. 2 Выбор (разветвление) – это набор действий, начинающийся с проверки некоторого условия. Результатом проверки может быть один из двух исходов: условие выполнено («ДА») или условие не выполнено («НЕТ»). Каждому из этих исходов могут соответствовать некоторые действия (рис. 3) или отсутствие каких-либо действий для одного из исходов (рис. 4). Обычно условие формулируется в виде логического выражения, вычисление которого в зависимости от результатов предшествующих действий дает значение истина («ДА») или ложь («НЕТ»). 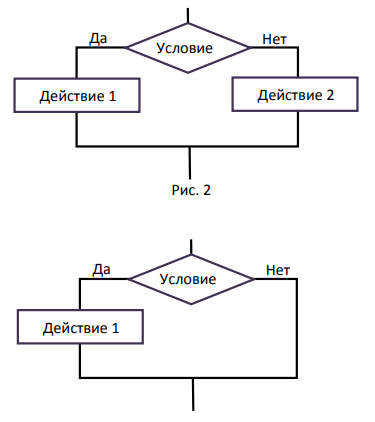  Рис. 3 Рис.4 Повторение (цикл) – это набор действий, которые могут выполняться многократно. Этот набор включает проверку условия, определяющего количество повторений цикла. Различают три варианта циклов: цикл с предусловием, цикл с постусловием, цикл с параметром. Цикл с предусловием («цикл-пока») (рис. 5) проверка условия является первым выполняемым действием; если результат проверки – «ДА», то выполняются другие действия цикла (тело цикла) и затем вновь проверка условия и т. д.; если результат проверки условия – «НЕТ», то цикл заканчивается. Действия цикла, следующие за проверкой условия, могут ни разу не выполниться, если результат первой проверки условия – «НЕТ» 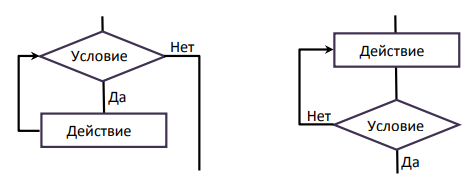 Рис. 5 Рис. 6 В цикле с постусловием («Цикл-до») (рис. 5) проверка условия является последним выполняемым в составе цикла действием; если результат проверки – «ДА», то цикл заканчивается; если результат проверки условия – «НЕТ», то вновь выполняются все предшествующие действия цикла и т. д. В отличие от цикла с предусловием все действия в цикле с постусловием всегда, по крайне мере, один раз выполняются. Для того чтобы циклы с пред- или постусловием заканчивались после какого-то количества повторений, действия внутри циклов должны изменять некоторые величины, влияющие на результат проверки условия. Само количество повторений таких циклов может быть заранее, до начала их выполнения, неизвестно. В тех случаях, когда число повторений известно заранее или определяется до начала цикла, может быть использован цикл с параметром. Такой цикл начинается с заголовка, содержащего параметр цикла с указанием его начального и конечного значений; за заголовком следуют действия, повторяемые в этом цикле. При каждом повторении цикла параметр возрастает (или убывает) на некоторую постоянную величину (шаг), изменяясь от начального до конечного значения. Набор действий, образующих цикл с параметром, показан на блок-схеме на рис. 7. 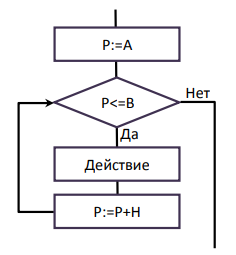 Рис. 7 Для упрощения блок-схем при изображении цикла с параметром можно использовать специальный блок-заголовок цикла с параметром. Такой вариант показан на рис. 8. 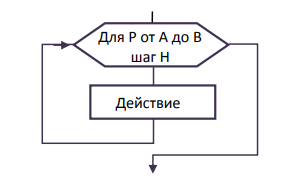 Рис. 8 Разберем примеры для лучшего понимания. Пример 1. Составить блок- схему для вычисления значения функции. 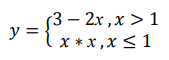 Эта функция не является элементарной, так как значение у зависит не только от значения аргумента х, но и от промежутка, к которому относится х. Блок-схема, вычисляющая значение функции представлена на Рис. 9 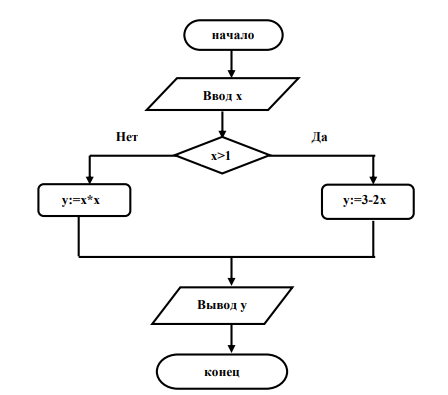 Рис. 9. Блок-схема решения примера 1. Рассмотрим свойства этого алгоритма. 1. Алгоритм обладает свойством дискретности, так как состоит из отдельных блоков, в каждом из которых записано одно указание (команда) алгоритма. 2. Алгоритм обладает свойством определённости, так как все его указания имеют однозначный смысл. 3. Он понятен исполнителю, умеющему сравнивать числа, вычислять их разность и произведение, значит, обладает свойством понятности. 4. Алгоритм вычисляет значение у для любого значения х, значит, обладает свойством массовости. 5. Результат для любого х достигается выполнением 4 указаний, значит, алгоритм обладает свойством результативности. 6. Алгоритм можно выполнить формально, даже не зная, что такое функция, поэтому он обладает свойством формальности. Пример 2. Имеются три контейнера – черный, белый и полосатый. В полосатом контейнере находятся белые и черные шары. Составить блок-схему процесса разложения шаров по контейнерам, соответствующим цвету шаров. Если решать задачу словестно, то алгоритм будет выглядеть так: 1. Достать шар из полосатого контейнера и перейти к шагу 2. 2. Если он белый, перейти к шагу 3, иначе перейти к шагу 4. 3. Опустить шар в белый контейнер и перейти к шагу 5. 4. Опустить шар в черный контейнер и перейти к шагу 5. 5. Если в полосатом контейнере еще есть шары, то перейти к шагу 1, иначе перейти к шагу 6. 6. Закончить процесс. Составим блок-схему процесса разложения белых и черных шаров из полосатого контейнера. 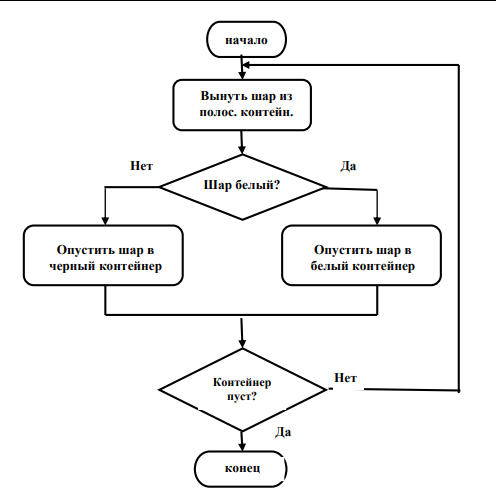 Рис.10. Блок-схема решения задачи 2. Рассмотрим свойства этого алгоритма: 1. Он дискретен, так как состоит из 6 отдельных указаний (шагов). 2. Все указания имеют однозначный смысл и не требуют от исполнителя решений, не предусмотренных алгоритмом, значит, он обладает свойством определенности. 3. Алгоритм понятен исполнителю, который умеет различать черный и белый цвета, понимает значение термина полосатый, значит, он обладает свойством понятности. 4. Алгоритм позволяет разложить по контейнерам любое количество шаров, значит, он обладает свойством массовости. 5. Для любого количества шаров алгоритм позволяет разложить их за конечное число шагов, поэтому он результативен. 6. Алгоритм формален, так как не требует от исполнителя никаких знаний и размышлений по поводу производимых действий. Пример 3. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1. Определить результат работы алгоритма для исходных данных Х = 7, Y = 12. 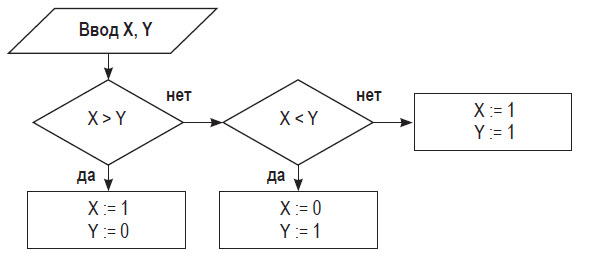 Решение. Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно). В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет». Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да». Вычисляется результат выполнения алгоритма: X := 0, Y := 1. Ответ: X := 0, Y := 1. |
