Числовые ряды. зан1_л38_13. Лекция 38 По учебной дисциплине Высшая математика Раздел 3 Математический анализ Тема 13 Ряды. Гармонический анализ Занятие 1 Числовые ряды содержание введение

• Название: Лекция 38 По учебной дисциплине Высшая математика Раздел 3 Математический анализ Тема 13 Ряды. Гармонический анализ Занятие 1 Числовые ряды содержание введение
• Анкор: Числовые ряды
• Дата: 14.05.2022
• Размер: 171.5 Kb.
• Имя файла: зан1_л38_13.doc
• Тип: Лекция; #529439

ЛЕКЦИЯ №38
По учебной дисциплине Высшая математика
Раздел № 3 Математический анализ
Тема № 13 Ряды. Гармонический анализ

Занятие № 1 Числовые ряды


СОДЕРЖАНИЕ

Введение

1. Основные понятия теории числовых рядов

2. Необходимый признак сходимости ряда

3. Свойства сходящихся рядов

4. Достаточные признаки сходимости числовых знакоположительных рядов

Заключение

Литература

1. В.С. Шипачев «Высшая математика», М., Высшая школа, 2005,

с. 379-388.
Учебно-материальное обеспечение

Мультимедийный комплект, презентация по теме занятия.
Формируемые компетенции
Способность представить современную картину мира на основе целостной системы естественнонаучных и математических знаний (ОК-1);

Владение культурой мышления, способность к обобщению, анализу, критическому осмыслению, систематизации, прогнозированию, постановке целей и выбору путей их достижения, умения анализировать логику рассуждений и высказываний (ОК-7).
Изучаемые дидактические единицы
Математический анализ
Воспитательные цели

Воспитывать уважение к профессии военного инженера; ответственное отношение к учёбе; аккуратность.

Учебные цели

После изучения темы курсанты должны:

знать:

- определение числового ряда;

- определение частичной суммы ряда;

- понятие сходящегося и расходящегося ряда;

- свойства сходящихся рядов;

- необходимый признак сходимости ряда;

- достаточные признаки сходимости рядов.
1. Основные понятия теории числовых рядов

Методические указания. Перед раскрытием содержания вопросов повторить основные вопросы теории прошлой лекции по теме 12. Для этого необходимо добиться четких ответов от обучающихся на следующие вопросы: общий вид ЛНДУ; структура общего решения ЛНДУ; теорема о подборе частного решения ЛНДУ по специальному виду правой части.

Построить изложение лекционного материала следующим образом: ввести понятие числового ряда, определение частичной суммы ряда; сформулировать определение сходящихся и расходящихся рядов.

Определение. Сумма членов бесконечной числовой последовательности называется числовым рядом.



При этом числа будем называть членами ряда, а u_n – общим членом ряда.
Определение. Суммы , n = 1, 2, … называются частными (частичными) суммами ряда.

Таким образом, возможно рассматривать последовательности частичных сумм ряда S₁, S₂, …,S_n, …

Определение. Ряд называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.



Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
2. Необходимый признак сходимости ряда

Методические указания. Сформулировать и доказать теорему, привести примеры.
Теорема. Если ряд сходится, то предел его общего члена при равен 0.


Доказательство. По условию ряд сходится, т.е. и

Распишем п-ую частичную сумму:

, тогда

Найдем предел:

Доказано.

Этот признак только необходимый, но не достаточный, т.е. обратная теорема не верна.

Пример. . Найдем предел общего члена: , но ряд расходится.

Выделить расходящиеся ряды:

, , ,
3. Свойства сходящихся рядов

Методические указания. Привести все свойства без доказательства.

1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.

2) Рассмотрим два ряда и , где С – постоянное число.

Теорема. Если ряд сходится и его сумма равна S, то ряд тоже сходится, и его сумма равна СS. (C 0)

3) Рассмотрим два ряда и . Суммой или разностью этих рядов будет называться ряд , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.

Теорема. Если ряды и сходятся и их суммы равны соответственно S и , то ряд тоже сходится и его сумма равна S + .



Разность двух сходящихся рядов также будет сходящимся рядом.

Сумма сходящегося и расходящегося рядов будет расходящимся рядом.

О сумме двух расходящихся рядов общего утверждения сделать нельзя.

При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.

4. Достаточные признаки сходимости числовых знакоположительных рядов
4.1. Признак сравнения рядов с неотрицательными членами.

Пусть даны два ряда и при u_n, v_n 0.

Теорема. Если u_n v_n при любом n, то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

Доказательство. Обозначим через S_nи _n частные суммы рядов и . Т.к. по условию теоремы ряд сходится, то его частные суммы ограничены, т.е. при всех n _n  M, где М – некоторое число. Но т.к. u_n v_n, то S_n _n то частные суммы ряда тоже ограничены, а этого достаточно для сходимости.

Пример. Исследовать на сходимость ряд

Т.к. , а гармонический ряд расходится, то расходится и ряд .

Пример. Исследовать на сходимость ряд

Т.к. , а ряд сходится ( как убывающая геометрическая прогрессия), то ряд тоже сходится.

Также используется следующий признак сходимости:

Теорема. Если и существует предел , где h – число, отличное от нуля, то ряды и ведут одинаково в смысле сходимости.
4.2. Признак Даламбера.

(Жан Лерон Даламбер (1717 – 1783) – французский математик)

Если для ряда с положительными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство



то ряд сходится, если же для всех достаточно больших n выполняется условие



то ряд расходится.

Предельный признак Даламбера.

Предельный признак Даламбера является следствием из приведенного выше признака Даламбера.

Если существует предел , то при  < 1 ряд сходится, а при  > 1 – расходится. Если  = 1, то на вопрос о сходимости ответить нельзя.
Пример. Определить сходимость ряда .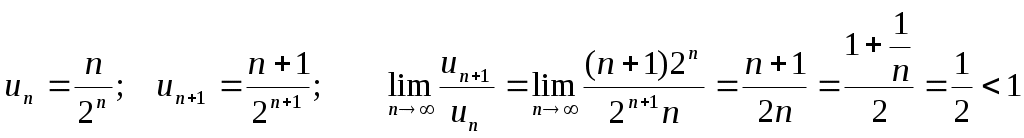



Вывод: ряд сходится.

Пример. Определить сходимость ряда



Вывод: ряд сходится.
4.3. Признак Коши. (радикальный признак)
Если для ряда с неотрицательными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство

,

то ряд сходится, если же для всех достаточно больших n выполняется неравенство



то ряд расходится.

Следствие. Если существует предел , то при <1 ряд сходится, а при >1 ряд расходится.
Пример. Определить сходимость ряда .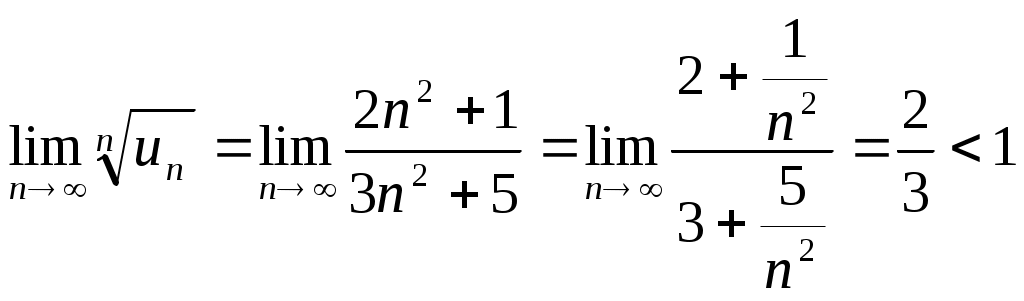



Вывод: ряд сходится.

Пример. Определить сходимость ряда .



Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.

,

таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.
4.4. Интегральный признак Коши.

Если (х) – непрерывная положительная функция, убывающая на промежутке [1;), то ряд (1) + (2) + …+ (n) + … = и несобственный интеграл одинаковы в смысле сходимости.

Пример. Ряд сходится при >1 и расходится 1 т.к. соответствующий несобственный интеграл сходится при >1 и расходится 1. Ряд называется общегармоническим рядом.
Следствие. Если f(x) и (х) – непрерывные функции на интервале (a, b] и то интегралы и ведут себя одинаково в смысле сходимости.