Лекция 4 Ступенчатая матрица. Ранг ступенчатой матрицы Определение
 Скачать 107.5 Kb.
|
|
Лекция 4 4.1. Ступенчатая матрица. Ранг ступенчатой матрицы Определение 4.1. . _______________________ матрицы называются следующие преобразования: 1) _________________ (строки или столбца) ________________________; 2) ______________________________________________________________ ___________________________________________ 3) ___________________________________ Замечание 4. Как правило, получается ________________ матрица _____________ данной. 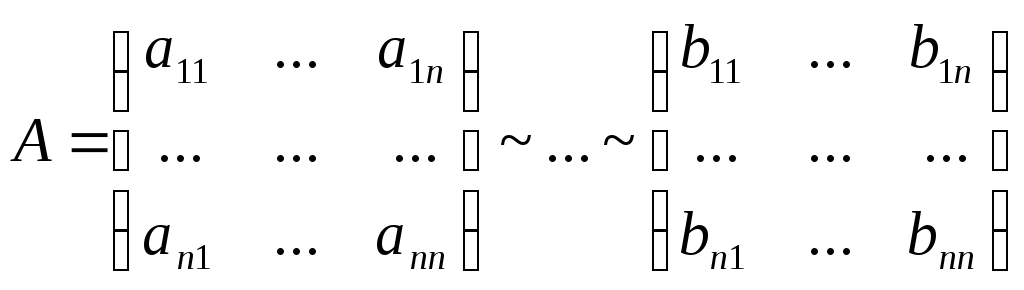 .Определение 4.2. Матрица, у которой в каждой следующей строке, начиная со второй, _________________________________________________ _________________________________________________________________, а все нулевые строки (состоящие только из нулей) стоят ___________________ строк (строк, содержащих хотя бы один ненулевой элемент), называется ___________________. Пример 4.1. 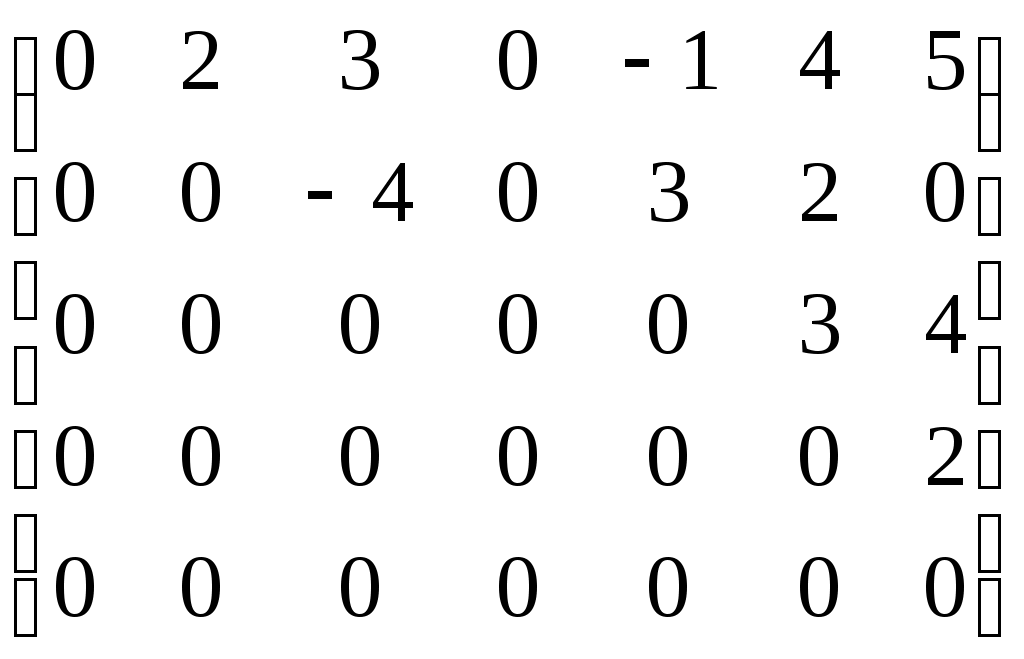 .Базисным минором, к примеру, данной матрицы является минор: Пример 4.2. С помощью элементарных преобразований привести матрицу 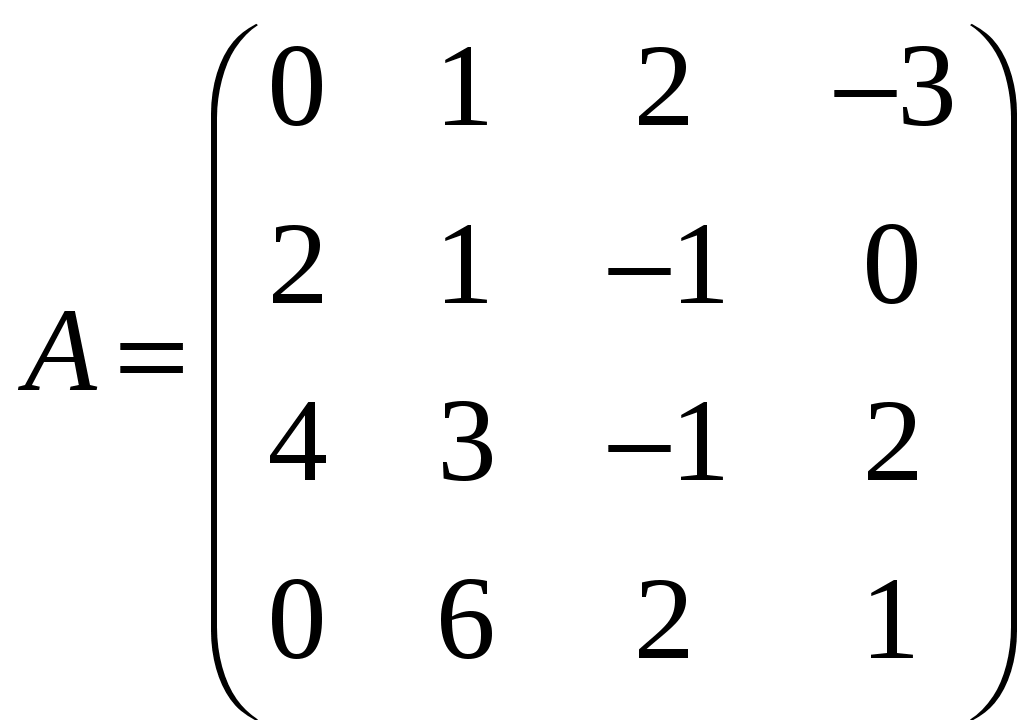 к ступенчатому виду.Решение. Теорема 4.1. ______________________________________________________ Теорема 4.2 (_________________________). 1) каждая матрица элементарными преобразованиями _____ приводится к ____________________матрице. 2) ________________________________________________________________ Доказательство возьмем ________________ столбец, содержащий _____________ элементы. _______________________________ так, чтобы один из ненулевых элементов этого столбца оказался __________________ (если первый элемент взятого столбца был равен нулю). С помощью преобразований строк можно получить новую матрицу, в которой все элементы под ____ окажутся равными _____ Чтобы получить нуль на месте элемента _________, достаточно умножить __-ю строку матрицы (где стоит ___) на число _____ и прибавить _-ой строке (где стоит __). Действительно, на месте элемента __ получим ______________ Обратим указанным способом ________________________ _________________ элементом. Первая строка ступенчатой матрицы готова: все ненулевые элементы ______________________ теперь стоят ___________ _____________________ элемента ___________ строки. Применим ту же операцию к матрице, начинающейся со второй строки и так далее. Так как строк – конечное число, то в результате получим ступенчатую матрицу. 2) пусть в ступенчатой матрице имеется __________________. Тогда каждый минор ____-го ___________ порядка содержит _______ строки (хотя бы одну) и потому равен _______. Но имеется хотя бы один минор _-го порядка ________________: наверняка _________________________________, главную диагональ которого образуют первые ненулевые элементы всех _ ненулевых строк. Действительно, такой минор равен ______________ ___________________________________________________________. Значит ______________. Пример 4.3. Придумать ступенчатую матрицу шестого порядка, чтобы  .Решение. Пример 4.4. Определить ранг матрицы приведением матрицы 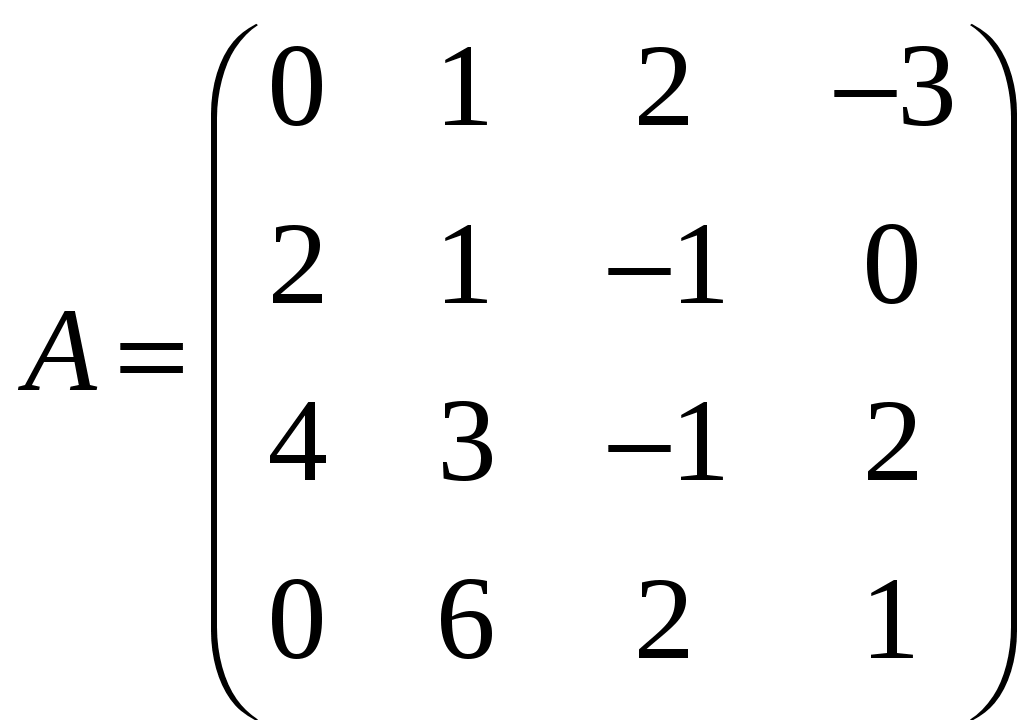к ступенчатому виду.Решение. 4.2. Теорема Кронекера-Капелли Пусть задана система: _ линейных уравнений c _ неизвестными: 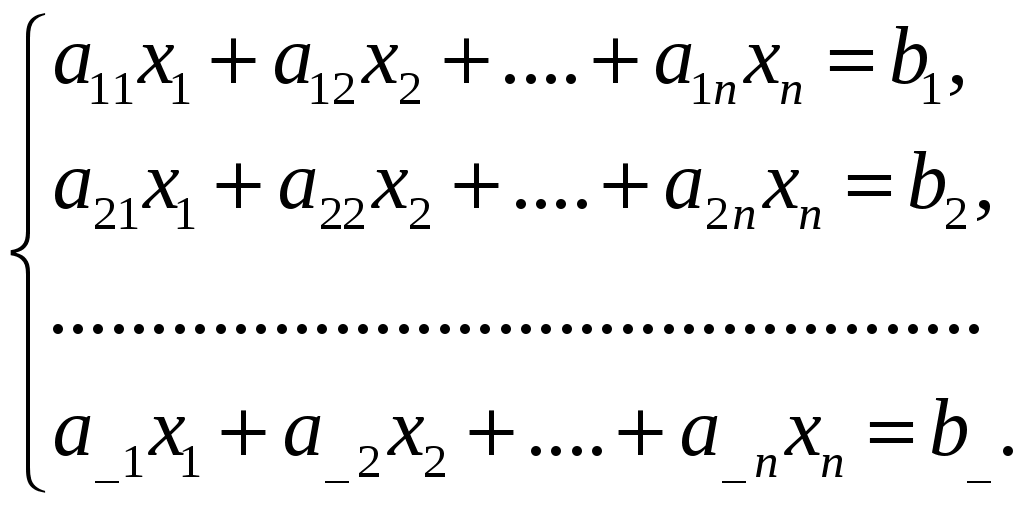 (4.1)Определение 4.3. 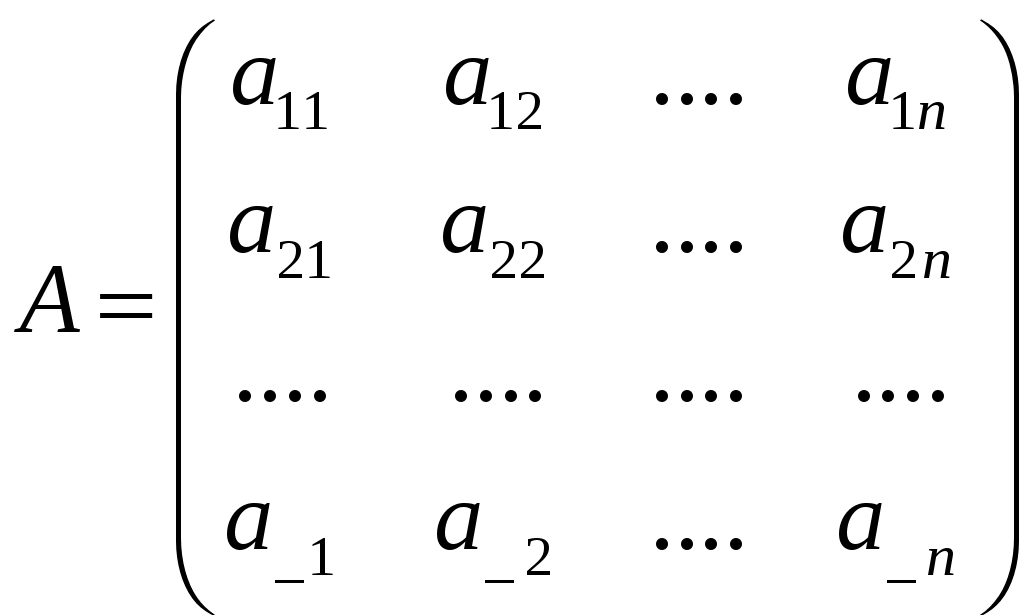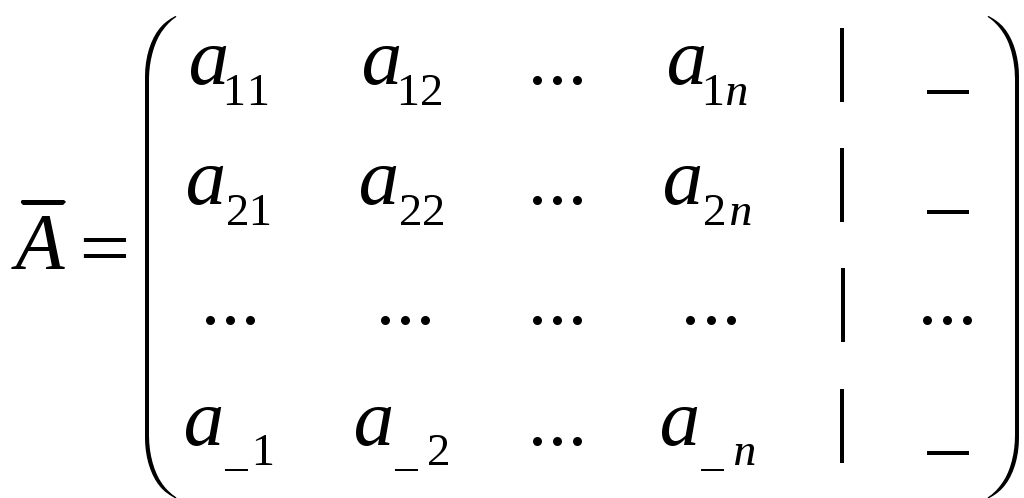1) матрица системы (4.1) коэффициентов при неизвестных  называется _________ матрицей системы 2) матрица  называется ______________ матрицей системы.Теорема 4.3 (___________________________). Система линейных уравнений (4.1) ___________ тогда и только тогда, когда __________. (4.2) Следствие 1 Система линейных уравнений (4.1) имеет _______________________, если _____________, где  – число _________________ в системе.Следствие 2 Если ___________, то система линейных уравнений (4.1) имеет ____________ _________________________ (т.е. система ____________________). Пример 4.5. Определить, является ли следующая система совместной: 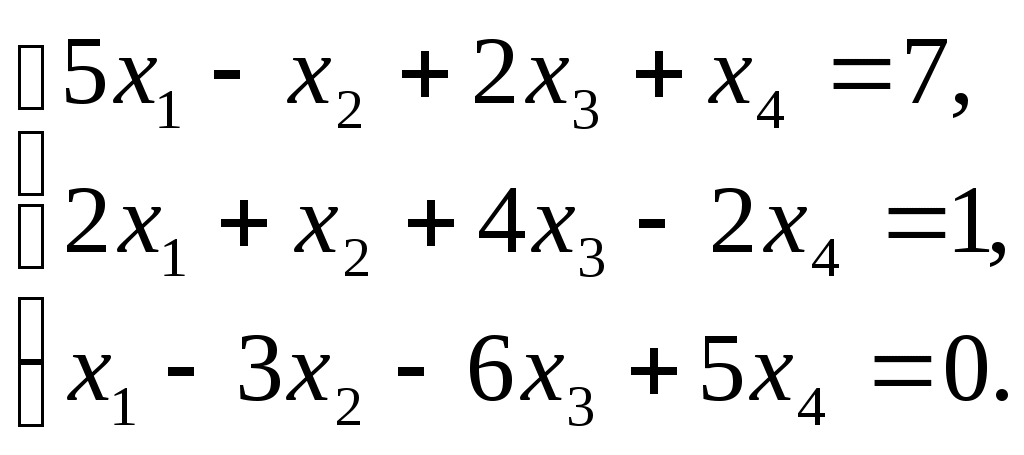 Решение. Как видно, _________________, поскольку ранги ___________, то по теореме 4.3 данная система ___________________ (__________________). 4.2. Метод Гаусса (метод последовательного исключения переменных) Определение 4.4. Если все свободные члены системы (4.1) равны ______, то система называется ___________________. Определение 4.5. Две системы называются ____________, если __________ ___________________ системы является ______________________________. Над системами можно производить следующие линейные преобразования: __________________________________; _____________________________________________________________; _____________________________________________________________ _________________________________________________________________________________________________________________________ . При исследовании и решении систем линейных уравнений производятся _______________________________________________________, в результате которых получится __________________________ матрица некоторой 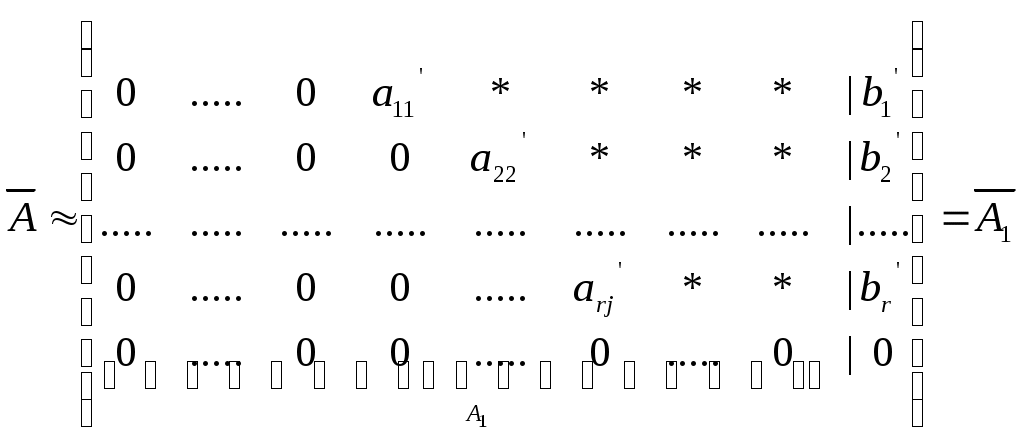______ ___________________________________________:  ,  . (4.3)Выберем в матрице  ненулевой минор порядка  , т.е. _________ минор (его можно выбрать на пересечении первых  строк и столбцов, с которых начинаются ненулевые элементы строк). Будем считать, что этот минор расположен в __________________ матрицы  Этот минор является ______________________ и равен произведению _______________________.Нулевые строки матрицы (им соответствуют уравнения _______________________), а также ______________столбцы отбросим Матрица примет вид: 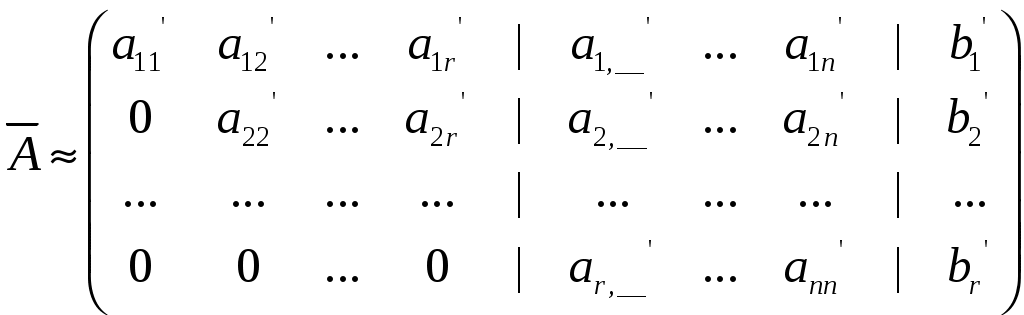 (4.4)Все элементы базисного минора _____________________ можно сделать равными _____, а элементы главной диагонали равными ________. Таким образом, исходная система (4.1) будет приведена к эквивалентной системе:  (4.5)или к системе 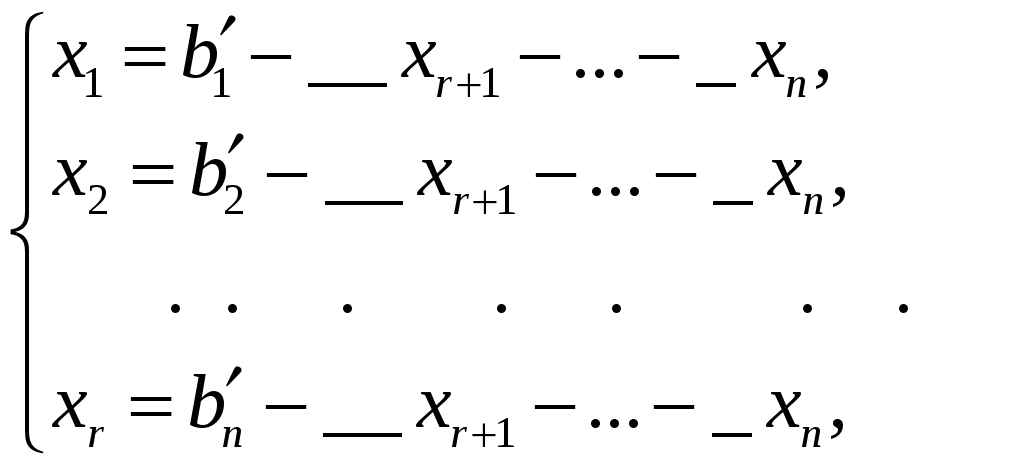 (4.6)из которой видно, что если _____, то система (4.6) имеет _______________ решение:  , …,  .Если 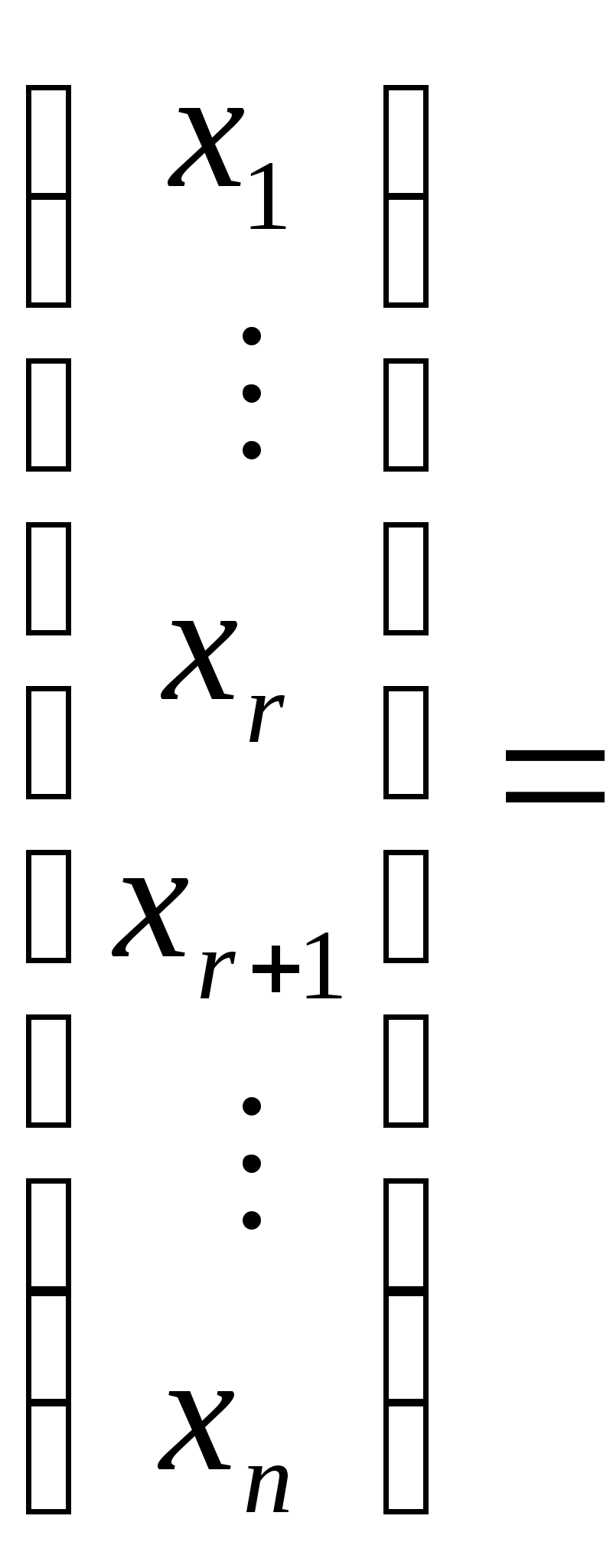 , то переменные  – ___________,  – ___________ и придавая им произвольные значения  , …,  , можно записать общее решение системы в виде: (4.7)Итак, метод Гаусса состоит в следующем: _____________ матрицу системы _____________________________ приводят к ______________ виду; ________________________________________ и делают вывод ___________________________________ системы; в случае _______________ системы в основной матрице _________ __________________ и дальнейшими элементарными преобразованиями ________ добиваются того, чтобы в этом миноре _______________ _______________________________________________________________ ___________________________________________________________; выписывают систему, соответствующую полученной расширенной матрице, после чего переписывают систему, ________________ __________________ и переведя остальные слагаемые в правую часть; если ________,то в ___________ стоят только _______________ и получено ___________________ решение; если _________, то в правой части ________________________. ____________ неизвестные выражаются _____________________. Полученные решения новой системы с _ главными неизвестными называется __________________ системы. Придавая ____________ неизвестным некоторые _________________, из общего решения находят соответствующие _____________________________________ и тем самым находят ________________ исходной системы уравнений. Пример 4.6. Решить следующую систему уравнений методом Гаусса: 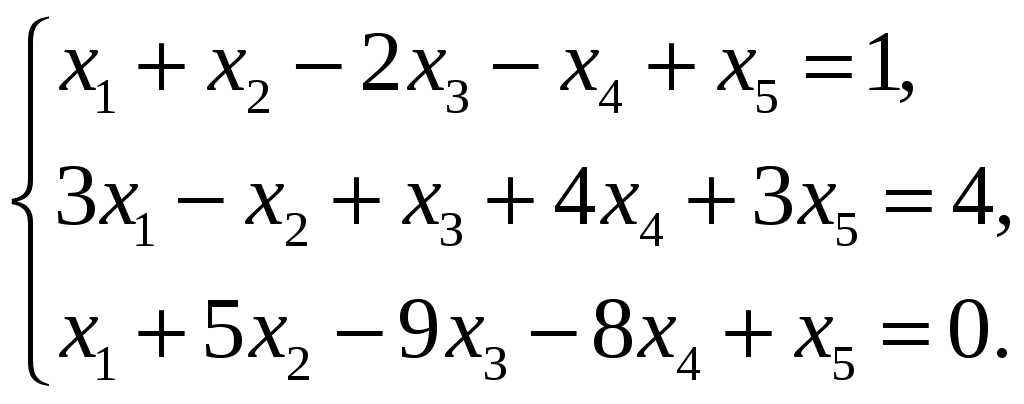 Решение. |