Лекция. Лекция 5. Лекція 5 Факторний аналіз
 Скачать 0.69 Mb.
|
|
Лекція 5 Факторний аналіз Дисперсійний аналіз застосовується для дослідження впливу однієї або декількох якісних змінних (факторів) на одну залежну кількісну змінну (відгук). Аналіз часових рядів застосуємо до одиночних або пов'язаним часових рядах і дозволяє виділяти різні форми періодичності і взаємовпливу часових процесів, а також здійснювати прогнозування майбутньої поведінки часового ряду. Регресивні процедури дозволяють розрахувати модель, що описується деяким рівнянням і відображає функціональну залежність між експериментальними кількісними змінними, а також перевіряють гіпотезу про адекватність моделі експериментальним даним. За отриманими результатами можна оцінити природу і ступінь залежності змінних і передбачити нові значення залежної змінної. Кореляційний аналіз - це група статистичних методів, спрямована на виявлення та математичне уявлення структурних залежностей між вибірками. Кластерний аналіз здійснює розбиття об'єктів на задане число віддалених один від одного класів, а також будує дерево класифікацій об'єктів за допомогою ієрархічного об'єднання їх в групи (кластери). Основним завданням факторного аналізу є знаходження в багатовимірному просторі первинних змінних (значення яких реєструються в експерименті), скороченою системи вторинних змінних (факторів). Факторний аналіз – статистичний метод перевірки гіпотез про вплив різних чинників на досліджувану випадкову величину. Розроблено і загальноприйнята модель, при якій вплив фактора представлено в лінійному вигляді. Дисперсійний аналіз, запропонований Р. Фішером, є статистичним методом, призначеним для виявлення впливу ряду окремих факторів на результати експерименту. В основі дисперсійного аналізу лежить припущення про те, що одні змінні можуть розглядатися як причини (фактори, незалежні змінні), а інші як слідства (залежні змінні). Незалежні змінні називають іноді регульованими чинниками саме тому, що в експерименті дослідник має можливість варіювати ними і аналізувати виходить результат. Сутність дисперсійного аналізу полягає в розчленуванні загальної дисперсії досліджуваного ознаки на окремі компоненти, зумовлені впливом конкретних факторів, і перевірці гіпотез про значущість впливу цих факторів на досліджуваний ознака. Порівнюючи компоненти дисперсії один з одним за допомогою F - критерію Фішера, можна визначити, яка частка загальної варіативності результативної ознаки зумовлена дією регульованих факторів. Вихідним матеріалом для дисперсійного аналізу є дані дослідження трьох і більше вибірок, які можуть бути як рівними, так і нерівними за чисельністю, як зв'язковими, так і незв'язними. За кількістю виявлених регульованих факторів дисперсійний аналіз може бути однофакторний (при цьому вивчається вплив одного фактора на результати експерименту), двофакторна (при вивченні впливу двох чинників) і багатофакторним (дозволяє оцінити не тільки вплив кожного з факторів окремо, але і їх взаємодія). Дисперсійний аналіз відноситься до групи параметричних методів і тому його слід застосовувати тільки тоді, коли доведено, що розподіл є нормальним. t – критерій Стьюдента, як відомо, дозволяє перевіряти гіпотези тільки про рівність середніх двох генеральних сукупностей. Однак часто перед дослідником стоїть завдання провести порівняння більшого числа совокупностей. Таке порівняння можна було б здійснити за допомогою спеціалізованих непараметричних критеріїв (Н - Круськала-Уоллеса, S - Джонкіра та інших). Використовуючи ж більш потужні параметричні методи, найбільш просто вирішити це завдання, попарно порівнюючи між собою сукупності за допомогою того ж t - критерію Стьюдента, однак такий підхід не є правильним. Справа в тому, що при зростанні числа груп стрімко збільшується число можливих пар, і ризик неправильного відкидання нульової гіпотези (т. Е. Ймовірність припуститися помилки першого роду - стверджувати, що відмінності між генеральними сукупностями реально існують, коли це фактично не так) значно перевищує встановлюваний дослідником рівень значимості. Більш коректним вирішенням цієї проблеми є застосування більш загального методу перевірки гіпотез про середні – так званого дисперсійного аналізу. Нехай генеральні сукупності X1 X2 Xp. Розподілені нормально і мають однакову, хоча і невідому дисперсію. Математичні очікування також невідомі, але можуть бути різні. Потрібно при заданому рівні значущості за вибірковими середнім перевірити нульову гіпотезу H0: M(X1)= M(X2)=…= M(Xp) про рівність всіх математичних очікувань. Іншими словами, потрібно встановити, значимо чи незначимо розрізняються вибіркові середні. Здавалося б, при порівнянні декількох середніх їх можна було б порівнювати попарно, проте зі зростанням числа середніх зростає і найбільша відмінність між ними: середня нової вибірки може виявитися більше найбільшого або менше найменшого із середніх, отриманих до нового іспиту. Тому для порівняння декількох середніх використовують інший метод, який заснований на порівнянні дисперсій і тому названий дисперсійним аналізом. Метод розвинений англійським статистиком Р. Фішером На практиці дисперсійний аналіз використовують, щоб встановити, чи істотний вплив деякого якісного фактору F, котрий має p рівнів F1 F2 Fp, на досліджувану випадкову величину X, наприклад, потрібно з'ясувати, який вид добрив. Якщо відмінність між цими дисперсіями значима, то фактор має істотний найбільш ефективний для отримання найбільшого врожаю. В цьому випадку якісний фактор F - добриво, а його рівні - види добрив. Основна ідея дисперсійного аналізу полягає в порівнянні «Факторної» дисперсії, яку породжує впливом фактора, і «Залишкової» дисперсії, обумовленої випадковими причинамивплив на випадкову величину X. В цьому випадку середні спостережуваних значень на кожному рівні (групові середні) розрізняються також значимо. Якщо вже встановлено, що фактор істотно впливає на випадкову величину X, а потрібно з'ясувати, який з рівнів фактора має найбільший вплив, то додатково виконують попарне порівняння середніх. Дисперсійний аналіз використовують також для встановлення однорідності декількох сукупностей (дисперсії цих сукупностей однакові за припущенням; якщо дисперсійний аналіз покаже, що математичні сподівання однакові, то в цьому сенсі сукупності однорідні). Однорідні сукупності можна об'єднувати в одну і тим самим отримати про неї більш повну інформацію, отже, і більш надійні висновки. У більш складних випадках досліджують вплив декількох факторів на кількох постійних або випадкових рівнях і з'ясовують вплив окремих рівнів та їх комбінацій (багатофакторний аналіз). Загальна, факторна і залишкова суми квадратів відхилень Розглянемо випадок однофакторного аналізу, коли на випадкову величину X впливає тільки один фактор F, котрий має p постійних рівнів. Нехай ознака X розподілений нормально. На нього впливає фактор F, котрий має p постійних рівнів. Будемо припускати, що число спостережень на кожному рівні постійно і дорівнює q. Таким чином, спостерігалося n = pq значень фактора, яким відповідають значення xij ознаки X, де i - номер випробування, 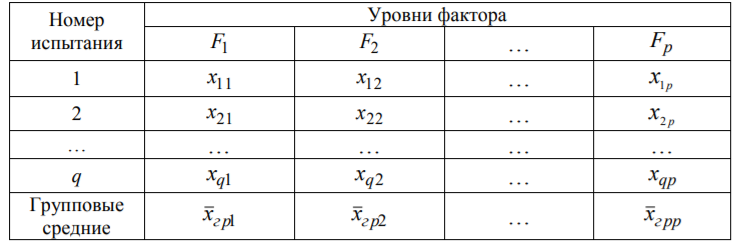 , j - номер рівня фактора,  . Результати спостережень зведені в таблицю Введемо в розгляд величини 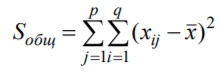 -загальна сума квадратів відхилень спостережуваних значень від загальної середньої x. 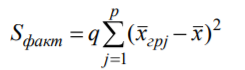 - факторная сума квадратів відхилень групових середніх від загальної середньої x. Вона характеризує розсіювання «між групами». 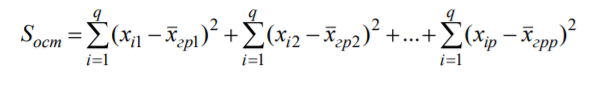 - - залишкова сума квадратів відхилень спостережуваних значень групи від своєї групової середньої, яка характеризує розсіювання «всередині групи». 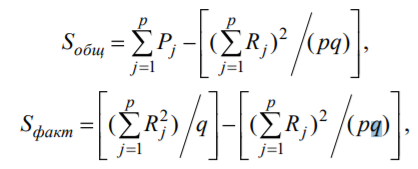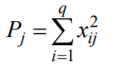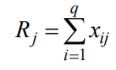Ці суми пов'язані рівністю:  Елементарними перетвореннями можна отримати формули, більш зручні для розрахунків:  де  – сума квадратів значень ознаки, відповідних рівню Fj (або говорять - на рівні Fj), – сума значень ознаки на рівні FjЗауваження 1. 1) Sфакт характеризує вплив фактора F. Припустимо, що фактор істотно впливає на ВВ X, тоді група значень, що спостерігаються на одному певному рівні, взагалі кажучи, відрізняється від груп спостережень на інших рівнях. отже, розрізняються і групові середні, причому вони тим більше розсіяні навколо загальної середньої, чим більшим виявиться вплив фактора. Звідси випливає, що для оцінки впливу фактора доцільно скласти суму квадратів відхилень групових середніх від загальної середньої (відхилення зводять в квадрат, щоб виключити погашення позитивних і негативних відхилень). Помноживши цю суму на q, отримаємо величину Sфакт, яка і відображає вплив фактора. 2) Sост характеризує вплив випадкових причин. Здавалося б, спостереження однієї групи не повинні відрізнятися. Однак, оскільки на X крім фактора F впливають і випадкові причини, спостереження однієї групи, взагалі кажучи, різні, а значить, розсіяні навколо своєї груповий середньої. Звідси випливає, що для оцінки впливу випадкових причин доцільно скласти суму квадратів відхилень спостережуваних значень кожної групи від своєї групової середньої, тобто Sост. 3) Sобщ відображає вплив і фактора, і випадкових причин. Будемо розглядати всі спостереження як єдину сукупність. Спостережувані значення ознаки різні внаслідок впливу фактора і випадкових причин. Для оцінки цього впливу доцільно скласти суму квадратів відхилень спостережуваних значень від загальної середньої. Зауваження 2. Для спрощення обчислень віднімають з кожного спостережуваного значення одне і те ж число C, приблизно рівне загальному середньому. Позначимо yij = xij - C. тоді 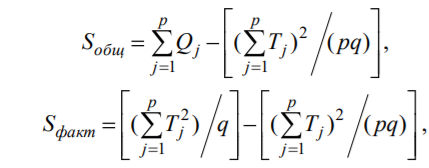 де 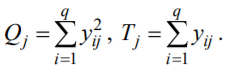 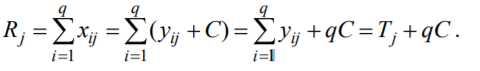 Загальна, факторна і залишкова дисперсії Розділивши суми квадратів відхилень на відповідне число ступенів свободи, отримаємо загальну, факторну і залишкову дисперсії: 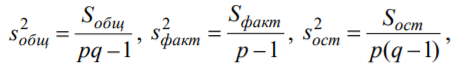 де p – число спостережень на кожному рівні, q – число рівнів, pq - 1 – число ступенів свободи загальної дисперсії, p - 1 – число ступенів свободи факторной дисперсії, p (q - 1) – число ступенів свободи залишкової дисперсії. Якщо нульова гіпотеза про рівність середніх справедлива, то всі ці дисперсії є незміщеними оцінками генеральної дисперсії. З огляду на, наприклад, що обсяг вибірки n= pq, робимо висновок, що 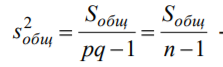 – виправлена вибіркова дисперсія, яка є незміщеною оцінкою генеральної дисперсії.Зауваження. Число ступенів свободи p(q - 1) залишкової дисперсії дорівнює різниці між числом ступенів свободи загальної та факторної дисперсій. Порівняння декількох середніх методом дисперсійного аналізу При заданому рівні значущості потрібно перевірити нульову гіпотезу про рівність декількох (p >2) середніх для нормальних сукупностей з невідомими, але однаковими дисперсіями. Покажемо, що рішення цього завдання зводиться до порівняння факторної і залишкової дисперсій за критерієм Фішера. 1) Нехай нульова гіпотеза про рівність декількох середніх (будемо називати їх груповими) справедлива. В цьому випадку факторна і залишкова дисперсії є незміщеними оцінками генеральної дисперсії і, отже, розрізняються незначимо. Якщо порівняти ці оцінки за критерієм Фішера, то, очевидно, критерій вкаже, що нульову гіпотезу про рівність факторної і залишкової дисперсій немає підстав відкинути. Таким чином, якщо гіпотеза про рівність групових середніх правильна, то вірна і гіпотеза про рівність факторної і залишкової дисперсій. 2) Нехай нульова гіпотеза про рівність групових середніх помилкова. В цьому випадку зі зростанням розбіжності між груповими середніми збільшується і факторна дисперсія, а разом з нею і відношення 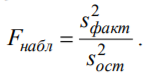 В результаті Fнабл виявиться більше Fкр, отже, гіпотеза про рівність факторної і залишкової дисперсій буде відкинута. Таким чином, якщо гіпотеза про рівність групових середніх помилкова, то помилкова і гіпотеза про рівність факторної і залишкової дисперсій. Від противного можна довести і справедливість зворотних тверджень: з правильності (хибності) гіпотези про рівність факторної і залишкової дисперсій слід правильність (хибність) гіпотези про середні. Отже, щоб перевірити гіпотезу про рівність групових середніх нормальних сукупностей з однаковими дисперсіями, досить перевірити за критерієм Фішера нульову гіпотезу про рівність факторної і залишкової дисперсій. В цьому і полягає метод дисперсійного аналізу. Зауваження 1. Якщо факторна дисперсія виявиться менше залишкової, то звідси вже випливає справедливість гіпотези про рівність групових середніх, і значить, немає необхідності вдаватися до критерію Фішера. Зауваження 2. Якщо немає впевненості в справедливості припущення про рівність дисперсій розглянутих сукупностей, то це припущення слід перевірити заздалегідь, наприклад, за критерієм Кочрена. Приклад 1. Проведено по 6 випробувань на кожному з трьох рівнів фактору А . Методом дисперсійного аналізу при рівні значущості 0,05 перевірити гіпотезу про рівність групових середніх. Передбачається, що вибірки отримані з нормально розподілених генеральних сукупностей з рівними дисперсіями. 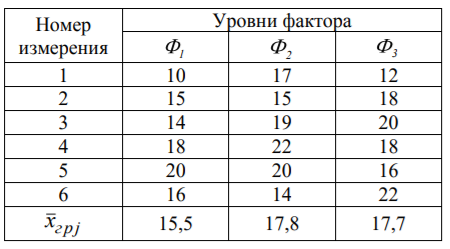 Розв’язок. Обчислимо загальне середнє  Для спрощення приймемо С=17 і перейдемо до умовних варіант. Складемо розрахункову таблицю 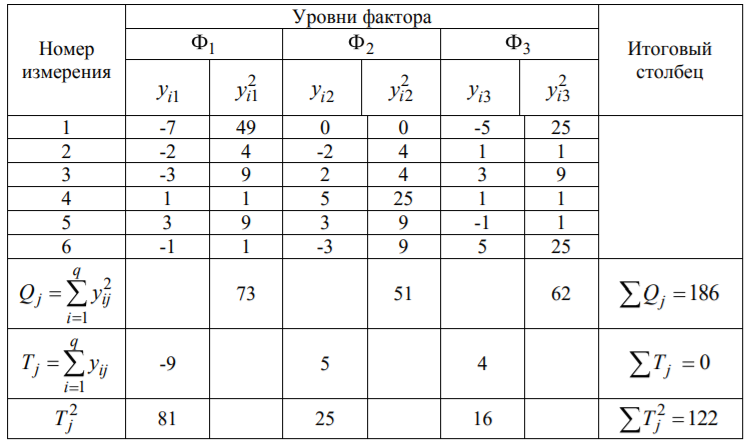 Знайдемо виправлені середньоквадратичні відхилення 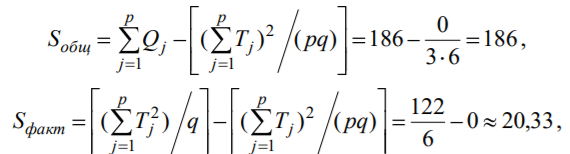  Обчислимо факторну та залишкову дисперсії 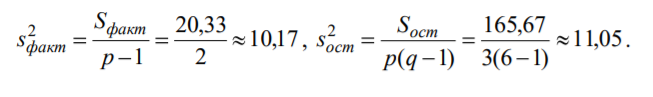 Факторна дисперсія виявилася менше залишкової, отже, навіть не застосовуючи критерій Фішера, можна зробити висновок, що немає підстав відкинути гіпотезу про рівність середніх, а значить, вплив фактора не значимий. Приклад 2. Фірма має досить великим запасом однотипного товару і розфасовує його в різні упаковки. В її розпорядженні є упаковки 3 видів. З метою вивчення впливу упаковки товару на рівень продажів 5 продавців протягом тижня пропонували даний товар покупцеві. Дані про продажі товару в трьох різних упаковках п'ятьма продавцями наведені в таблиці. Методом дисперсійного аналізу при рівні значущості 0,05 перевірити, чи значимий вплив виду упаковки на рівень продажів. Передбачається, що вибірки отримані з нормально розподілених генеральних сукупностей з рівними дисперсіями. 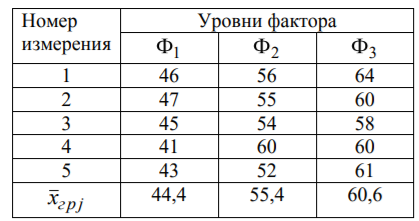 Розв’язок. Обчислимо загальне середнє 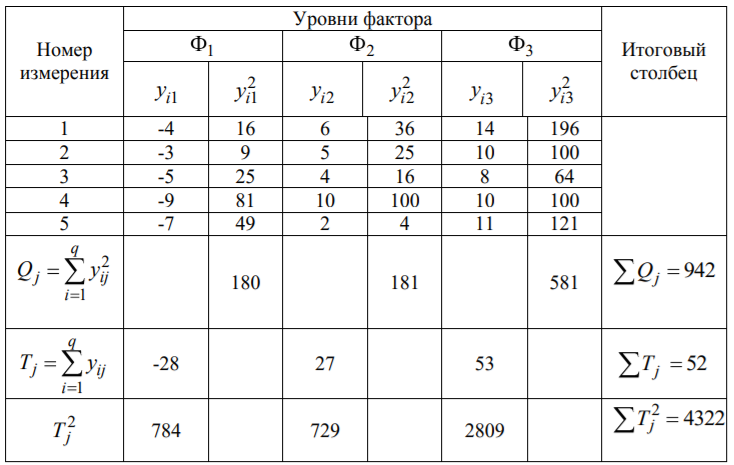 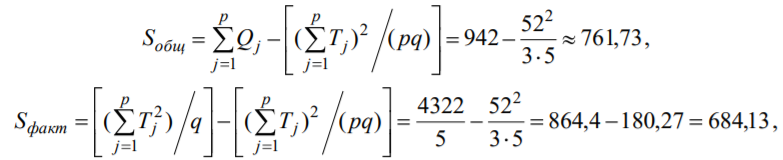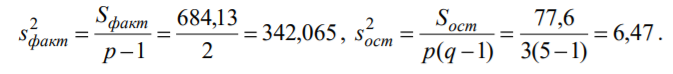. Перейдемо до умовнх варіант і побудуємо розрахункову таблицю    За обчисленими даними знайдемо спостережуване значення критерію Фішера: 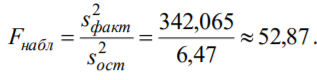 За заданим рівнем значущості 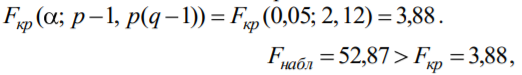 і числом ступенів свободи p - 1, p(q - 1) по таблиці з додатків знайдемо критичну точку отже, немає підстав прийняти нульову гіпотезу про рівність групових середніх (вона відхиляється на даному рівні значущості), тобто групові середні різняться значимо. Таким чином, вплив фактора значимо. Тобто вид упаковки значимо впливає на обсяги продажів товару. Статистичне моделювання Статистичне моделювання – базовий метод моделювання, що полягає в тому, що модель випробовується множиною випадкових сигналів із заданою щільністю ймовірності. Метою є статистичне визначення вихідних результатів. В основі статистичного моделювання лежить метод Монте-Карло. Нагадаємо, що імітацію використовують тоді, коли інші методи застосувати неможливо. Метод Монте-Карло можна визначити як метод моделювання випадкових величин з метою обчислення характеристик їх розподілів. Виникнення ідеї використання випадкових явищ в області наближених обчислень прийнято відносити до 1878 р коли з'явилася робота Холла про визначення числа p за допомогою випадкових кидань голки на розграфлений паралельними лініями папір. Щодо суті, то вона полягає в тому, щоб експериментально відтворити подію, імовірність якої виражається через число p, і приблизно оцінити цю імовірність. Спочатку метод Монте-Карло використовувався головним чином для вирішення завдань нейтронної фізики, де традиційні чисельні методи виявилися мало придатними. Далі його вплив поширився на широкий клас задач статистичної фізики, дуже різних за своїм змістом. Метод Монте-Карло зробив і продовжує робити істотний вплив на розвиток методів обчислювальної математики (наприклад, розвиток методів чисельного інтегрування) і при вирішенні багатьох завдань успішно поєднується з іншими обчислювальними методами і доповнює їх. Його застосування виправдане в першу чергу в тих завданнях, які допускають теоретико-імовірнісний опис. Це пояснюється як природністю отримання відповіді з деякою заданою вірогідністю в задачах з імовірнісним змістом, так і істотним спрощенням процедури вирішення. Випробування повторюється N раз, причому кожен досвід не залежить від інших, і результати всіх дослідів усереднюються. Це означає, що число випробувань повинно бути досить велике, тому метод істотно спирається на можливості комп'ютера. Теоретичною основою методу Монте-Карло є граничні теореми теорії ймовірностей. Вони гарантують високу якість статистичних оцінок при досить великому числі випробувань. Метод статистичних випробувань застосуємо для дослідження як стохастичних, так і детермінованих систем. Практична реалізація методу Монте-Карло неможлива без використання комп'ютера. Найпростіший випадок використання методу Монте-Карло - визначення площі під графіком функції. Для цього необхідно обмежити функцію фігурою, чия площа відома або легко обраховуються (S), потім «накидати» в цю фігуру кілька точок (N) і підрахувати, скільки точок потрапило всередину графіка (I). Площа області, обмеженою графіком функції і осями координат буде дорівнює S * (I / N). Суть методу Монте-Карло полягає в наступному: потрібно знайти значення а деякої досліджуваної величини. Для цього вибирають таку випадкову величину X, математичне очікування якої дорівнює а: М (Х) = а. Практично роблять так: виконують п випробувань, в результаті яких отримують п можливих значень X, обчислюють їх середнє арифметичне і приймають його в якості оцінки (наближеного значення) а* шуканого числа а. Відшукання можливих значень випадкової величини Х (моделювання) називають «розігрування випадкової величини». Розглянемо приклад, який ілюструє метод статистичних випробувань: Система контролю якості продукції складається з трьох приладів. Імовірність безвідмовної роботи кожного з них протягом часу Т дорівнює 5/6. Прилади виходять з ладу незалежно один від одного. При відмові хоча б одного приладу вся система перестає працювати. Знайти ймовірність Рвідм того, що система відмовить за час Т. Аналітичне рішення. Подія А (вихід з ладу хоча б одного з трьох приладів за час Т) і подія  (жоден з трьох приладів не вийде з ладу за час Т) - протилежні. Імовірність Р (А) = (5/6) 3. шукана ймовірністьРвідм=Р(А)=  Тепер вирішимо завдання методом статистичних випробувань. Нагадаємо, що при використанні даного методу можливі два підходи: або безпосередньо проводять експерименти, або імітують їх іншими експериментами, що мають з вихідними однакову вірогідну структуру. В умовах даної задачі «натуральний» експеримент-спостереження за роботою системи протягом часу Т. Багаторазове повторення цього експерименту може виявитися важко здійснюваним або просто неможливим. Замінимо цей експеримент іншим. Для визначення того, чи вийде або не вийде з ладу за час Т окремий прилад, будемо підкидати гральну кістку. Якщо випаде одне очко, то будемо вважати, що прилад вийшов з ладу; якщо два, три, ..., шість очок, то будемо вважати, що прилад працював безвідмовно. Імовірність того, що випаде одне очко, так само як і ймовірність виходу приладу з ладу, дорівнює 1/6, а ймовірність того, що випаде будь-яке інше число очок, як і ймовірність безвідмовної роботи приладу, дорівнює 5/6. Щоб визначити, відмовить чи ні вся система за час Т, будемо підкидати три гральні кістки (або одну кістку три рази). Якщо хоча б на одній з трьох кісток випаде одне очко, то це буде означати, що система відмовила. Повторимо випробування, що складається в підкиданні трьох гральних кісток, багато разів поспіль і знайдемо відношення числа т «відмов» системи до загальної кількості п проведених випробувань. імовірність відмови  Випадкові числа. Раніше було зазначено, що метод Монте-Карло заснований на застосуванні випадкових чисел; дамо визначення цих чисел. Позначимо через R ytперервну випадкову величину, розподілену рівномірно в інтервалі (0, 1). Випадковими числами називають можливі значення rj yеперервної випадкової величини R, розподіленої рівномірно в інтервалі (О, 1). Насправді користуються не рівномірно розподіленої випадкової величиною R, можливі значення якої мають нескінченне число десяткових знаків, а квазіравномерной випадковою величиною R*, можливі значення якої мають кінцеве число знаків. В результаті заміни R на R* розігрується величина має не точно, а наближено заданий розподіл. У додатку наведена таблиця випадкових чисел. Випадкова величина R* має властивість: ймовірність попадання її в будь-який інтервал, що належить інтервалу (0; 1) дорівнює довжині цього інтервалу. Функція щільності fR*(x) = 1; інтегральна функція FR*(x) = x; математичне очікування МR*(x) = 1/2; дисперсія DR*(x) = 1/12. Розігрування дискретної випадкової величини. Нехай потрібно розіграти ДВВ з відомим законом розподілу:
Позначимо рівномірно розподілене ВВ в інтервалі (0, 1) через R, а її можливі значення (випадкові числа) - rj. Розіб'ємо інтервал [0, 1) точками з координатами р1, р1 + р2,, р1 + р2 + р3, ..., р1 + р2 + р3 + ... + рn-1 на n часткових інтервалів:  Довжина Di кожного з них дорівнює ймовірності рi. Далі чинимо так: вибираємо з таблиці випадкових чисел яке-небудь випадкове число rj, якщо воно потрапило в інтервал Di, то розігрувана ВВ прийняла можливе значення хi. Приклад: ДВВ задана законом розподілу:
Розіграти 8 значень даної ДВВ. Розіб'ємо інтервал (0, 1) на часткові інтервали:  Випишемо з таблиці випадкових чисел 8 значень: 0,1; 0,37; 0,08; 0,99; 0,12; 0,66; 0,31; 0,85. Визначимо до якого інтервалу належить кожне з цих чисел і отримаємо відповідні значення ДВВ:  і т.д.Розігрування протилежних подій. Нехай потрібно розіграти випробування в кожному з яких подія А з'являється з імовірністю р і не з'являється з ймовірністю 1-р. Замінимо протилежні події А і випадковою величиною Х. Вважатимемо, що, якщо значення ВВ Х дорівнює 0, то сталося , якщо ВВ прийняла значення 1, то відбулася подія А. Тоді розігрування протилежних подій зводиться до розіграшу ДВВ Х з відомим законом розподілу.Приклад: Розіграти 5 випробувань, в кожному з яких подія А з'являється з імовірністю р = 0,35. Замінимо А і ДВВ Х, яка має закон розподілу:
Отримаємо два інтервали  З таблиці випишемо 5 випадкових чисел: 0,1; 0,36; 0,08; 0,99; 0,12. Отримаємо наступні значення ДВВ Х: 1, 0, 1, 0, 1. Їм відповідають події: А, , А, , А.Розігрування повної групи подій. При розігруванні повної групи несумісних подій надходять також, як при розігруванні протилежних подій. Події повної групи замінюють будь-якими числами, наприклад послідовністю натуральних чисел 1,2,3 ..., тоді отримуємо ДВВ Х з відомим законом розподілу, правило розігрування значень якої вже було розглянуто. Приклад: Події А і В незалежні і сумісні. Розіграти 6 випробувань, в кожному з яких, ймовірність появи А дорівнює 0,6, ймовірність появи В дорівнює 0,2. Складемо повну групу подій і обчислимо ймовірності їх появ, використовуючи теорему множення ймовірностей незалежних подій. Можливі 4 виходи: 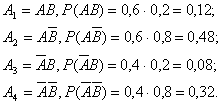 Перевірка 0,12+0,48+0,08+0,32=1. Замінимо події числами 1, 2, 3, 4 з відповідними можливостями, отримаємо ДВВ Х з законом розподілу:
Розіб'ємо інтервал (0, 1) на часткові інтервали (0; 0,12), (0,12; 0,6), (0,6; 0,68), (0,68; 1). Випишемо 6 випадкових чисел: 0,45; 0,65; 0,06; 0,59; 0,33; 0,7. Отримаємо значення ДСВХ: 2, 3, 1, 2, 2, 4. Визначаємо відповідні події: А2, А3, А1, А2, А2, А4. Розігрування неперервної випадкової величини. 1.Метод зворотних функцій. Нехай потрібно разиuрать НВВ Х, знаючи функцію розподілу F(x). Скористаємося теоремою: Якщо ri – випадкове число, то можливе значення хi розігрується НВВ Х із заданою функцією розподілу F(x), відповідне ri, є коренем рівняння F(xi) =ri . На підставі даної теореми сформулюємо правило розігрування значень НВВ Х, знаючи її функцію розподілу F(x): Необхідно вибрати випадкове число ri, прирівняти його функції розподілу і вирішити щодо хi рівняння: F(xi) = ri. Приклад: НВВ Х розподілена по показовому закону. потрібно знайти явну формулу для розігрування можливих значень Х. Відомо, що функція розподілу під час показового законі має вигляд  Складемо і вирішимо щодо х рівняння:    Вибираючи випадкові числа ri, підставляючи їх в отриману явну формулу, розіграємо можливі значення НВВ Х. Якщо відома щільність розподілу НВВ Х, то для розігрування значень НСВХ, вирішують рівняння:  Метод суперпозиції. Нехай функція розподілу розігрується НВВ Х задана лінійною комбінацією двох функцій розподілу: F(x) = C1 F1(x) + C2 F2 (x), де C1> 0, C2> 0. При  кожна з функцій розподілу прямує до одиниці,, тому C1 + C2 = 1.Введемо допоміжну ДВВ Z з законом розподілу:
Виберемо два незалежних випадкових числа r1 і r2. За кількістю r1 розіграємо можливе значення Z. Якщо z = 1, то можливе значення х знайдемо з рівняння F1(x) = r1, а якщо z = 2, то з рівняння F2(x) = r2. Приклад: Знайти явні формули для розігрування НСВХ, заданої функцією розподілу: F(x) = 1- 0,25(e-2x + 3e-x). Використовуючи метод суперпозиції, уявімо функцію у вигляді F(x) =0,25(1 – e-2x) +0,75 (1 – e-x). С1 =0,25; С2 =0,75; F1(x) = 1 – e-2x, F2(x) = 1 – e-x. Введемо ДВВ Z
Інтервал (0; 1) розіб'ємо на часткові інтервали (0; 0,25) і (0,25; 1). Виберемо випадкові числа r1 і r2. Якщо r1 належить інтервалу (0; 0,25), то вирішуємо рівняння: 1 – e-2x= r2, якщо (0,25; 1), то 1 – e-x = r2. |