.лекция №6. Лекция №6. Лекция 6. Аксонометрические проекции план 1 Виды аксонометрических проекций
 Скачать 1.8 Mb. Скачать 1.8 Mb.
|
|
Дисциплина: «Инженерная графика. Строительное черчение». Курс 1, группа ПС-11 ПС-12 Лекция №6. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ План: 6.1 Виды аксонометрических проекций. 6.2 Прямоугольные проекции. 6.3 Косоугольные проекции. 6.4 Оси координат в диметрической и изометрической проекциях. 6.5 Изометрия плоских многоугольников. 6.6 Построение окружности в изометрии и диметрии. Построение эллипса. 6.7 Аксонометрия детали. 6.8 Последовательность построения аксонометрических проекций предмета. 6.9 Построение детали в фронтальной диметрической и изометрической проекциях. 6.10 Штриховка сечений. 6.1Виды аксонометрических проекций. Аксонометрическая проекция (аксонометрия) – изображение геометрической фигуры, которое получается путем параллельного проецирования ее на некоторую плоскость П' вместе с декартовой системой прямоугольных координат 0XYZ, к которой она отнесена в пространстве. Чтобы чертеж стал измеримым, на плоскость чертежа проецируют систему координат 0XYZ таким образом, чтобы оси координат были параллельны направлениям длины, ширины и высоты изображаемого предмета. Аксонометрию используют в тех случаях, когда требуется дать более наглядное по сравнению с комплексным чертежом изображение предмета. Метод пpямоугольного пpоециpования на несколько плоскостей пpоекций, обладая многими достоинствами, вместе с тем имеет и существенный недостаток: изображения не обладают наглядностью. Одновpеменноe pассмотpение двух (а иногда и более) изобpажений затpудняет мысленное воссоздание пpостpанственного объекта. Пpи выполнении технических чеpтежей часто оказывается необходимым наpяду с изобpажением пpедметов в системе оpтогональных пpоекций иметь изобpажения более наглядные. Для постpоения таких изобpажений пpименяют способ аксонометpического пpоециpования, состоящий в том, что данный пpедмет вместе с системой тpех взаимно пеpпендикуляpных осей кооpдинат, к котоpым он отнесен в пpостpанстве, паpаллельно пpоециpуется на некотоpую плоскость, называемую плоскостью аксонометpических пpоекций (или каpтинной плоскостью). Пpоекция на этой плоскости называется аксонометpической или сокpащенно аксонометpией. Hа pис. 2.1.1 показана схема пpоециpования осей кооpдинат и отнесенной к ним точки А на плоскость P, пpинятую за плоскость аксонометpических пpоекций (каpтинную). Hапpавление пpоециpования указано стpелкой S. 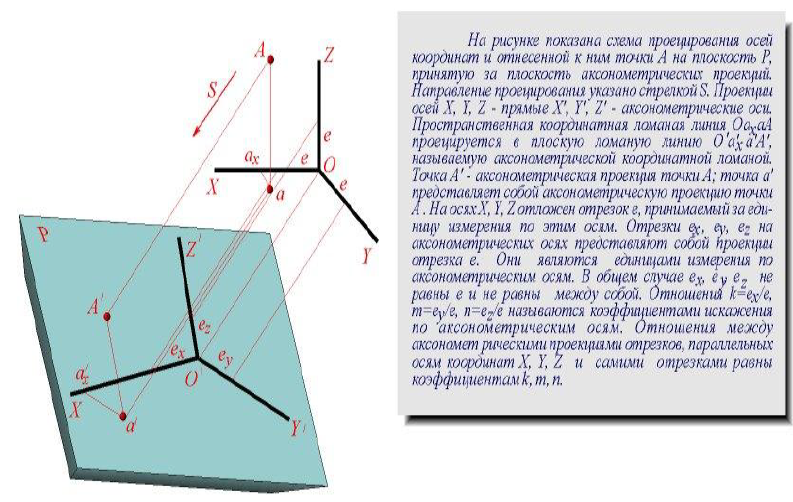 Рис. 2.1.1 Пpоекции осей X, Y, Z - пpямые X', Y', Z' называются аксонометpическими осями. Пpостpанственная кооpдинатная ломаная линия O ax a A пpоециpуется в плоскую ломаную линию O' a'x a' A', называемую аксонометpической кооpдинатной ломаной. Точка A'- аксонометpическая пpоекция точки A; точка a' пpедставляет собой аксонометpическую пpоекцию точки a. Аксонометpическую пpоекцию любой оpтогональной пpоекции точки A называют втоpичной пpоекцией точки A. Hа осях X, Y, Z отложен отpезок е, пpинимаемый за единицу измеpения по этим осям. Отpезки ex, ey, ez на аксонометpических осях пpедставляют собой пpоекции отpезка e. Они являются единицами измеpения по аксонометpическим осям. В общем случае ex, ey, ez не pавны e и не pавны между собой. Отношения k = ex /e, m = ey /e, n = ez /e называются коэффициентами (или показателями) искажения по аксонометpическим осям. Отношения между аксонометpическими пpоекциями отpезков, паpаллельных осям кооpдинат X, Y, Z и самими отpезками pавны коэффициентам k, m, n. Коэффициенты искажения и угол v, обpазованный напpавлением пpоециpования с каpтинной плоскостью, связаны зависимостью k2 + m2 + n2 = 2 + ctg2(v) Так как взаимное pасположение каpтинной плоскости P и кооpдинатных осей X, Y, Z, а также напpавление пpоециpования могут быть pазличными, то можно получать множество pазличных аксонометpических пpоекций. Если напpавление пpоециpования не пеpпендикуляpно к каpтинной плоскости P, то аксонометpическая пpоекция называется косоугольной; если же пеpпендикуляpно, - то пpямоугольной. Если все тpи показателя искажений между собой не pавны, то пpоекция называется тpиметpической; если два показателя искажения pавны (напpимеp, k = n), а тpетий отличен от них, то пpоекция называется диметpической; наконец, если все тpи показателя pавны (k = m = n), то пpоекция называется изометpической. В пpактике большое pаспpостpанение получили пpямоугольные изометpическая и диметpическая пpоекции. В реальном или учебном проектировании согласно ГОСТ 2.317—60 Аксонометрические проекции подразделяются на следующие виды: -Прямоугольные, где проецирующие лучи перпендикулярны картинной плоскости, прямоугольные проекции в свою очередь делятся: на прямоугольную изометрическую, где углы между осями Z, X, Y равны 120°, а углы между горизонтальной прямой и осями X и Y равны 30°, где изображение по всем трем осям не сокращается и обозначается индексом сокращения 1; на прямоугольную диметрическую проекцию, где ось X направлена к горизонтальной прямой под углом 7° 10', ось Y направлена к горизонтальной прямой под углом 41°25'. Индекс сокращения изображения по осям Z и X равен . 1, а индекс сокращения по оси Y равен 1/2; -Косоугольные проекции, где проецирующие лучи наклонны к картинной плоскости. Косоугольные проекции в свою очередь делятся: на фронтальную изометрическую проекцию, где угол между осями Z и X равен 90°, а угол оси Y к горизонтальной прямой равен 45°. Индексы сокращения по всем трем осям Z, X, Y равен 1; на горизонтальную изометрическую проекцию, где угол, под которым ось X встречается с горизонтальной прямой, равен 60°, а угол встречи оси Y с горизонтальной прямой 30°. Индекс сокращения по всем трем осям Z, X, Y равен 1; на фронтальную диметрическую проекцию, где угол между осями Z и X равен 90°, а ось Y встречается с горизонтальной прямой под углом в 45°. Индекс искажения по осям Z и X равен 1, а индекс искажения по оси Y равен 1/2; триметрическая проекция отличается разными показателями индекса искажения по всем трем осям. С горизонтальной прямая ось X встречается под углом 60°, ось Y под углом 15°, между осями X и Y угол равен 105°. Количественные показатели индексов искажения по трем осям в определенных пределах могут меняться. Коэффициенты искажения ИЗОМЕТPИЧЕСКАЯ ПPОЕКЦИЯ Так как k = m = n, то 3k2 = 2, k = 0,82, следовательно, коэффициенты искажения по осям X', Y', Z' = 0,82. Изометpическую пpоекцию для упpощения, как пpавило, выполняют без искажения по осям X', Y', Z', т.е. пpиняв коэффициент искажения pавным 1, что соответствует увеличению линейных pазмеpов изобpажения по сpавнению с действительными в 1/0,82 = 1,22 pаза. ДИМЕТPИЧЕСКАЯ ПPОЕКЦИЯ Если взять n = k и m = 1/2 k, то получим 2k2 + k2 /4 = 2, k2 = 8/9, k = 0,94, следовательно, по осям X' и Z' коэффициенты искажения k = n = 0,94, а по оси Y' коэффициент искажения m = 0,47. Диметpическую пpоекцию, как пpавило, выполняют без искажения по осям X' и Z' и с коэффициентом искажения 0,5 по оси X'. В этом случае линейные pазмеpы увеличиваются в 1/0,94 = 1,06 pаза. 2.2 Прямоугольные проекции. Изометрическая проекция (рис.2.2.1 и 2.2.2) характеризуется равенством углов между осями Х, Y, и Z, которые составляют 120 градусов. Истинные коэффициенты искажения по осям координат равны 0,82. При построении обычно применяют их приведенные значения, равные 1. 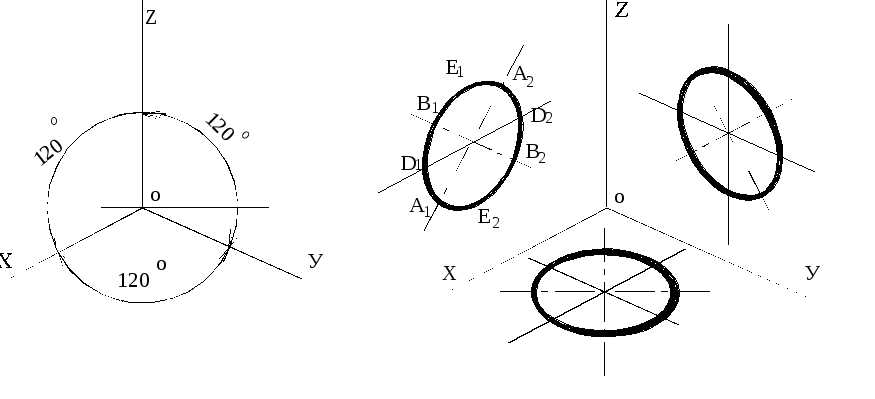 Рис. 2.2.1 Рис.2.2.2 Окружности, плоскости которых параллельны плоскостям координат, проецируется на плоскость чертежа в виде эллипсов (рис. 2.2.2). При построениях по приведенным коэффициентам искажения большая ось эллипса равна 1,22 D, а малая ось равна 0,71 D, где D - диаметр проецируемой окружности. При использовании истинных коэффициентов искажения большая ось эллипса равна D, а малая ось - 0,58D. На рисунке 2.2.2 показано построение восьми точек эллипса во фронтальной плоскости изометрической проекции. Большая ось эллипса А1А2 равна 1,22D и расположена под углом 90 градусов к оси Y. Малая ось В1В2 равна 0,71D и расположена параллельно оси Y (А1В1//А2В2// Е1Е2). Диаметры D1D2 и Е1 Е2 равны D. Большие оси эллипсов, расположенных в горизонтальной (ХОY) и профильной (YОZ) плоскостях изометрической проекции, перпендикулярны соответственно осям Z и Х. Диметрическая проекция (рис. 2.2.3), как правило, строится по приведенным коэффициентам искажения, которые по осям Х и Z равны 1, а по оси Y - 0,5. Оси Х и Y проводятся под указанными углами. Окружности, расположенные параллельно плоскостям координат, в аксонометрии изображаются в виде эллипсов. Большая ось эллипсов 1,2,3 при использовании истинных коэффициентов искажения, равна 1,06D, малая ось эллипса 1- 0,95D, а эллипсов 2 и 3 – 0,35D. 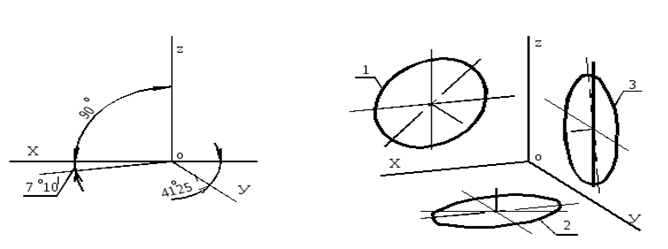 Рис.2.2.3 Рис. 2.2.4 Изометрия (прямоугольная) 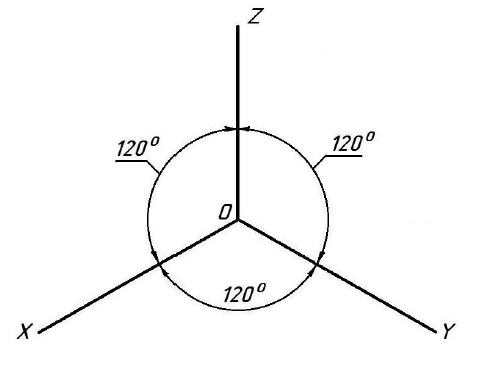 Рис. 2.2.5 Натуральные коэффициенты искажения по всем трем осям равны (k = m = n = 0,82). Приведенные коэффициенты искажения K = M = N = 1. По приведённым коэффициентам искажения масштаб чертежа увеличивается в 1,22 раза (1:0,82 = 1,22). Расположение осей в прямоугольной изометрии приведено на рис. 2.2.5. Диметрия (прямоугольная) Положение аксонометрических осей изображено на рис. 2.2.6. Действительные коэффициенты искажения для прямоугольной диметрии по осям X и Z равны 0,94 (k = n = 0,94), а по оси Z– 0,47 (m = 0,47), т. е. размеры, параллельные оси Y, уменьшаются в два раза. Приведенные коэффициенты искажения соответственно равны: K = N = 1; M = 0,5. Таким образом, пользуясь приведенными коэффициентами искажения, получают изображение, увеличенное в 1,06 раза по сравнению с натуральным. 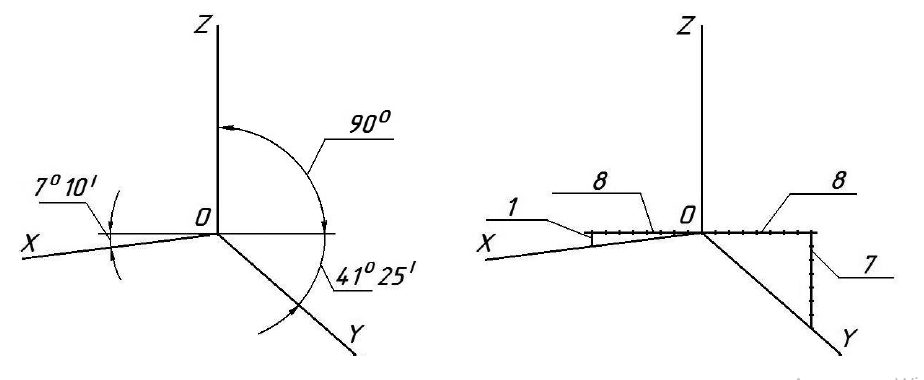 Рис. 2.2.6 2.3 Косоугольные проекции. Фронтальная изометрическая проекция обычно выполняется по приведенным коэффициентам искажения для осей Х, Y и Z, равным 1. Направление аксонометрических осей показано на рисунке 3.3.1. Допускается также располагать ось Y под углом 30 и 60 градусов. Окружности, расположенные в плоскостях, параллельных фронтальной плоскости ХОZ, изображаются в аксонометрии без искажения, а окружности, параллельные горизонтальной (ХОY) и профильной (YОZ) плоскостям проекций (координат) - в виде эллипсов. Большие оси эллипсов равны 1,3D и составляют с соответствующими осями Х или Z углы, равные 22 градусам 30 минутам, а малые оси – 054D (рис. 2.3.2). 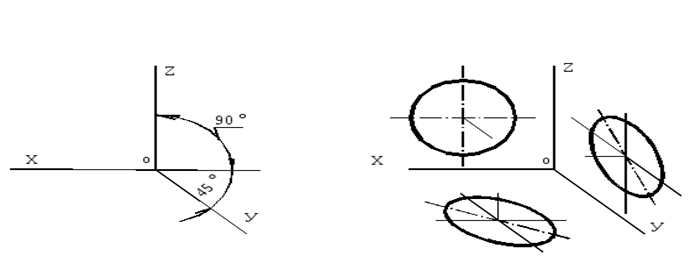 Рис. 2.3.1 Рис. 2.3.2 Горизонтальная изометрическая проекция также выполняется без искажения по осям X, Y и Z. Направление аксонометрических осей показано на рисунке 2.3.4. Допускается ось Y располагать под углом 45 и 60 градусов при сохранении угла между осями Х и Y, равного 90 градусам. 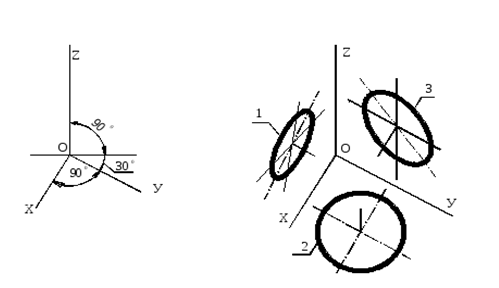 Рис. 2.3.4 Рис. 2.3.5 Окружности (рис.2.3.5), расположенные в плоскостях, параллельных горизонтальной плоскости ХОY, изображаются на аксонометрии без искажения, а параллельные фронтальной и профильной плоскостям проекций – в виде эллипсов. Большая ось эллипса 1 равна 1,37D и составляет с осью Z угол 15 градусов, малая ось – 0,54D. Большая ось эллипса 3 равна 1,22D и составляет с осью Z угол 30 градусов, малая ось - 0,71D. Фронтальная диметрическая проекция выполняется с коэффициентами искажения по осям Х и Z равными 1, а по оси Y - 0,5. Направление аксонометрических осей показано на рисунке 2.3.6. Допускается располагать ось Y под углом 30 и 60 градусов. Окружности, расположенные в плоскостях, параллельных фронтальной плоскости ХОZ, изображаются в аксонометрии без искажения, а окружности, параллельные горизонтальной и профильной плоскостям проекций – в виде эллипсов. Большие оси эллипсов равны 1,07D и составляют с соответствующими осями Х и Z углы, равные 7 градусам 14 минутам. Малые оси эллипсов равны 0,33D (рис. 2.3.7). 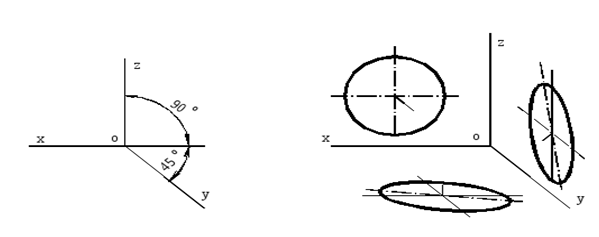 Рис. 2.3.6 Рис. 2.3.7 Диметрия (косоугольная или фронтальная) Этот вид аксонометрии получается проецированием системы координат на плоскость К, параллельную плоскости проекций П2. Положение аксонометрических осей изображено на рис. 2.3.8. Коэффициенты искажения являются точными и равными К = N = 1, М = 0,5. 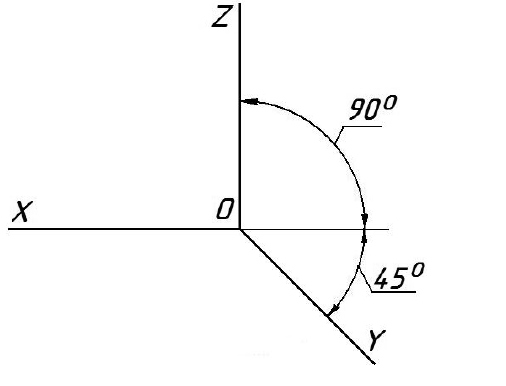 Рис. 2.3.8 2.4 Оси координат в диметрической и изометрической проекциях. Построение аксонометрических проекций начинают с проведения аксонометрических осей. Положение осей. Оси фронтальной диметрической проекции располагают, как показано на рис. 2.4.1, а: ось х - горизонтально, ось z - вертикально, ось у - под углом 45° к горизонтальной линии. Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 2.4.1, б. Положение осей изометрической проекции показано на рис. 2.4.1, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 2.4.1, д). Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О. При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название "диметрия", что по-гречески означает "двойное измерение". При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название "изометрия", что по-гречески означает "равные измерения". На рис. 2.4.1, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 2.4.1, в). Наклон оси в 30° (рис. 2.4.1, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток). 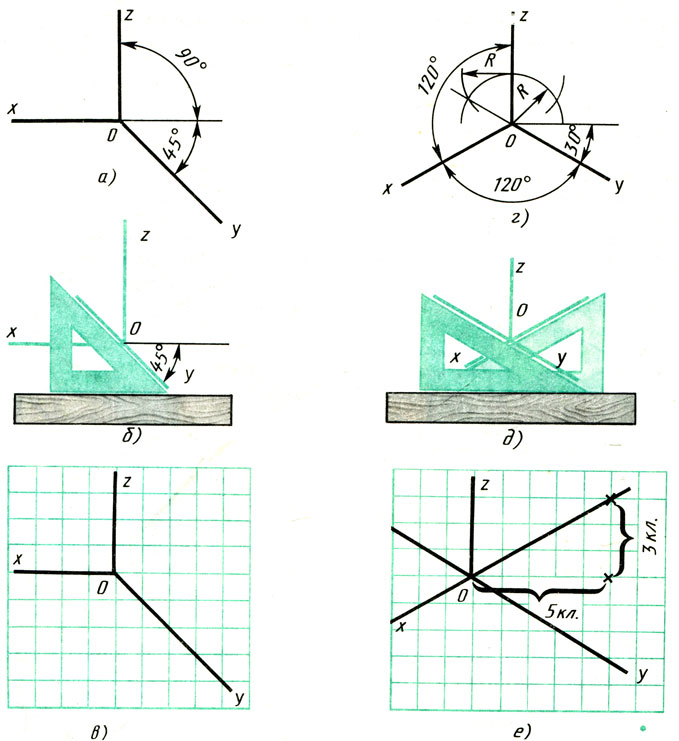 Рис. 2.4.1 В конструкторской документации применяются следующие виды аксонометрических проекций, приведенные в ГОСТ 2.317-2011: 1) 1)прямоугольные: изометрическая и диметрическая; 2) косоугольные: фронтальная и горизонтальная изометрическая, фронтальная диметрическая. Рассмотрим первый вид проекции, как наиболее употребительный. Положение осей в прямоугольной изометрической проекции и прямоугольной диметрической приведено на рис. 2.4.2, а и б соответственно. 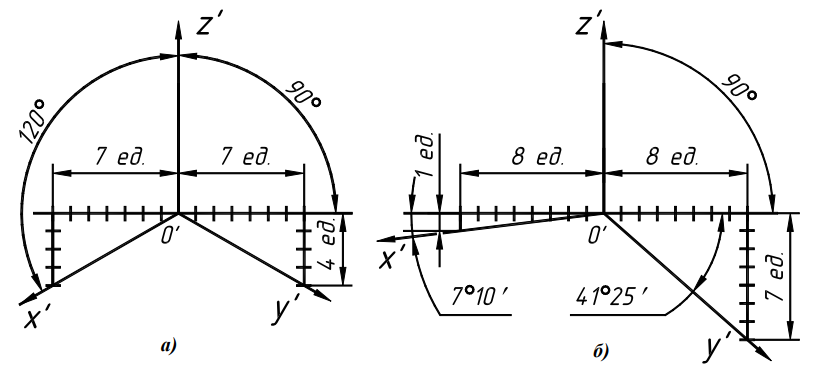 Рис. 2.4.2 Искажение размеров в изометрической проекции равно 0,82, а в диметрической, по осям X, Y, Z соответственно: 0,94; 0,47; 0,94. Для простоты построения принято, что в изометрии по осям показатель искажения равен 1, а в диметрии соответственно 1; 0,5; 1. Поэтому изометрическое изображение увеличивается в 1,22 раза, а диметрической в 1,06 раза. 2.5 Изометрия плоских многоугольников. Построение и вид плоских многоугольников в изометрии зависит от того, какой плоскости проекций параллелен данный многоугольник. На рис. 2.5.1, а) приведены многоугольники и их прямоугольные изометрические проекции (рис. 2.5.1, б, в, г) в зависимости от их расположения относительно координатных плоскостей комплексного чертежа. Рис. 2.5.1, б) – плоскости многоугольников параллельны П1; рис. 2.5.1, в) – плоскости многоугольников параллельны П2. На рис. 2.5.1, г) – плоскости многоугольников параллельны П3. 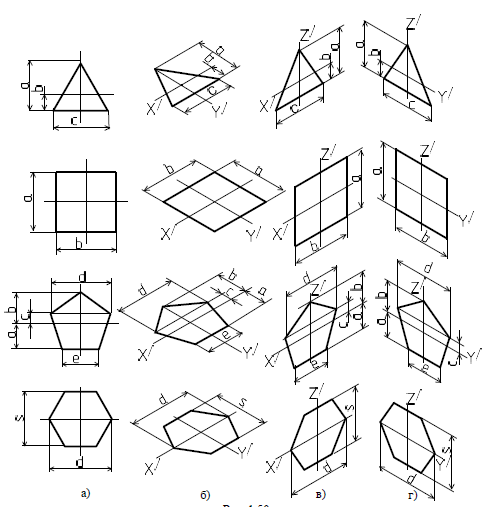 Рис. 2.5.1 При построении изометрических проекций следует помнить, что размеры необходимо откладывать параллельно аксонометрическим осям или использовать координаты точек, замеренные на комплексном чертеже. Если плоскость многоугольника является плоскостью общего положения, то построение его изометрии осуществляется по координатам вершин. Построение аксонометрических проекций вершин осуществляют с помощью координатных ломаных (рис. 2.5.2). 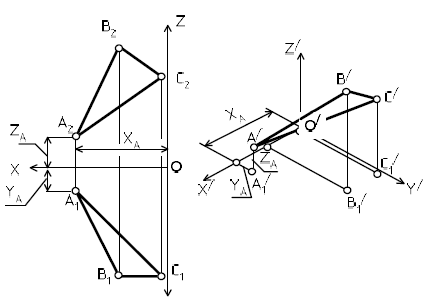 Рис. 2.5.2 2.6 Построение окружности в изометрии и диметрии. Окружности, принадлежащие плоскостям проекций или плоскостям им параллельным, проецируются на аксонометрическую плоскость проекций в эллипсы. В изометрии такой эллипс имеет большую ось 1,22, а малую 0,71 диаметра окружности. В диметрии окружность проецируется в эллипсы с осями 1,06 и 0,35, если плоскость ее параллельна горизонтальной и профильной плоскостям проекций. В целях упрощения построений вместо эллипсов строят четырехцентовые овалы. Правило расположения осей овалов. Большая ось овала всегда перпендикулярна той аксонометрической оси, которая не принадлежит плоскости окружности. На рис. 2.6.1, а приведено изображение изометрии окружности, расположенной в плоскостях x0z (1 ), y0z (2 ), x0y (3 ). На рис. 2.6.1, б приведено изображение диметрии окружности, расположенной в разных плоскостях. 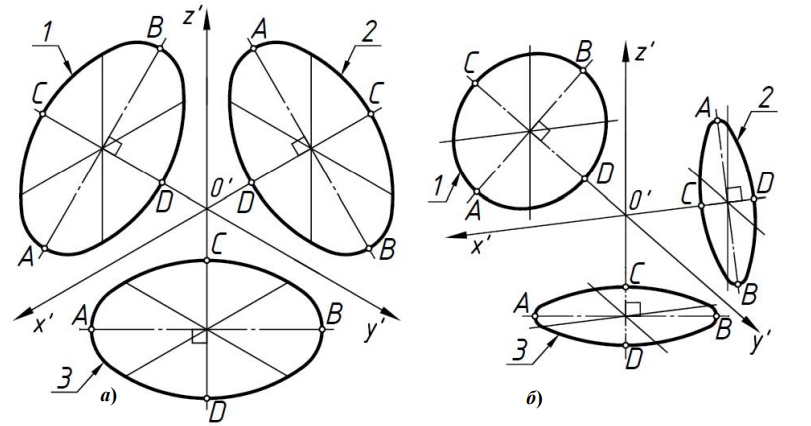 Рис. 2.6.1 Если плоскость окружности параллельна фронтальной плоскости проекций, то эллипс имеет большую ось 1,06, а малую 0,95 диаметра окружности. Построение овала с большой осью АВ = 1,06d и малой осью СD = 0,94d (овал 1, см. рис. 2.6.1) показано на рис. 2.6.2. Такой эллипс можно заменить при построении обычной окружностью диаметра d. 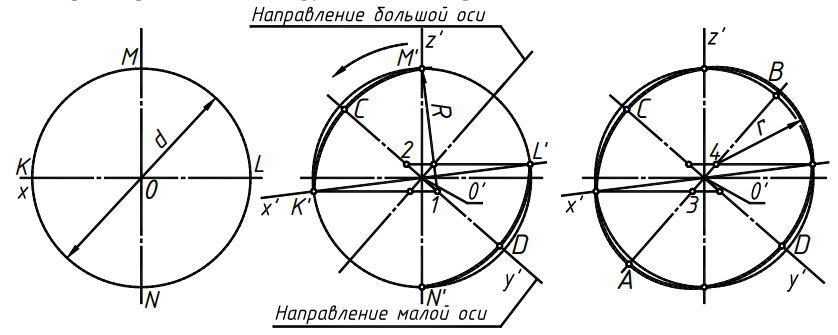 Рис. 2.6.2 Один из рекомендуемых способов построения овалов показан на рис. 2.6.3. Здесь построены овалы для окружности, расположенной в горизонтальной плоскости (рис. 2.6.3, а – изометрия, рис. 2.6.3, б – диметрия).  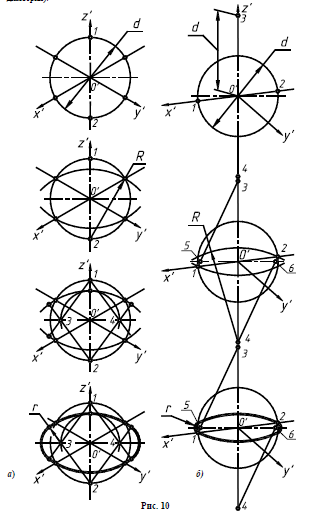 Рис. 2.6.3 Построение окружности в изометрии. Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 2.6.4). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов. 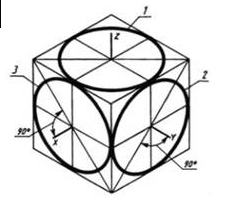 Рис.2.6.4 Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 2.6.5). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 2.6.5, а). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности. 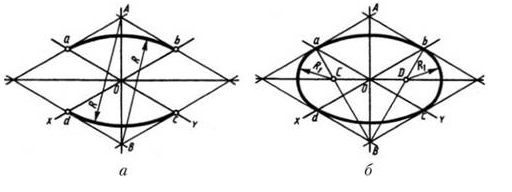 Рис.2.6.5 Из вершин тупых углов (точек А и В) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 2.6.5, б). Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие. Малые дуги описывают радиусом R, равным отрезку Са (Db). Построение окружности в диметрии ГОСТ 2.317-69 определяет положение окружностей, лежащих в плоскостях, параллельных плоскостям проекций для прямоугольной изометрической проекции и для прямоугольной диметрии. 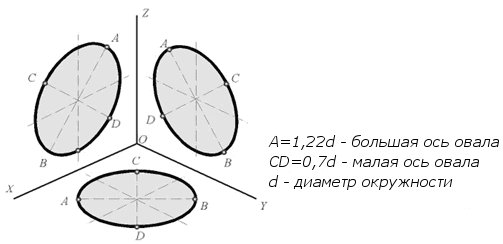 Рис. 2.6.6 Построение изометрической проекции окружности показано на рисунке 2.6.7. Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось - 0.71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая - 0.58 диаметра окружности. 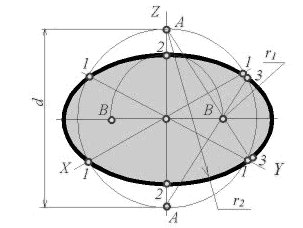 Рис. 2.6.7 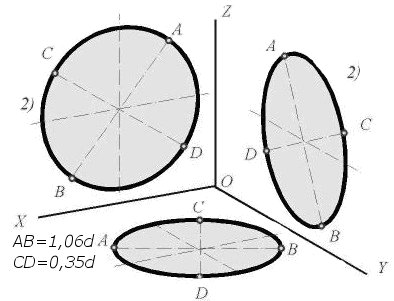 Рис. 2.6.8 Построение диметрической проекции окружности представлено на рисунке 2.6.9. Если диметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности. Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0,33 диаметра окружности. 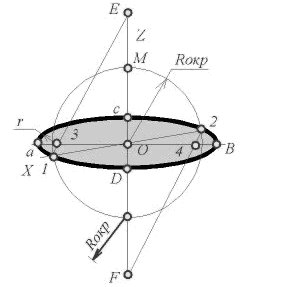 Рис. 2.6.9 Как бы ни была расположена плоскость окружности, сначала целесообразно построить параллелограмм A*B*C*D* – параллельную проекцию квадрата ABCD, описанного около данной окружности, а затем с помощью восьми точек и восьми касательных вписать в него эллипс. Точки 1, 3, 5 и 7 – середины сторон параллелограмма. На отрезке 3*B*, как на гипотенузе, построить прямоугольный равнобедренный треугольник 3*KB*; из точки 3* радиусом 3*K описать полуокружность, которая пересечет A*B* в точках L и M; эти точки делят отрезок 3*A* и равный ему отрезок 3*B* в отношении 3:7; через точки L и М провести прямые параллельные боковым сторонам параллелограмма, и отметить точки 2*, 4*, 6* и 8* расположенные на диагоналях. Построить касательные к эллипсу в найденных точках. Касательные t2 и t6 параллельны BD, а касательные t4 и t8 параллельны AC. Получив восемь точек и столько же касательных, можно с достаточной точностью вычертить эллипс (рисунок 2.6.10). 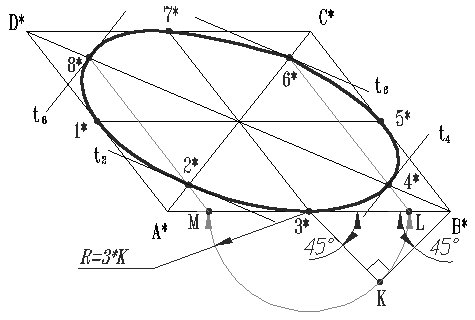 Рис. 2.6.10 2.7 Аксонометрия детали. Выполнение деталей в аксонометрии поясним на примере выполнения корпуса вентиля (рис.2.7.1). Даны вертикальная и горизонтальная проекции детали. Построение аксонометрического изображения начинаем с выбора вида аксонометрической проекции. Для данного геометрического образа удобнее использовать изометрию, так как все окружности, лежащие в различных плоскостях, будут изображаться одинаковыми по форме эллипсами. Построение начинаем с вычерчивания осей Х, Y, Z. По оси Х симметрично точке О1 откладываем отрезок 12, который соответствует длине корпуса, т.е. определяем положение левого и правого торцов боковых фланцев. Из начала координат проводим окружность, радиус которой равен 1,22* радиуса центральной внешней сферы корпуса, а по оси Z – расстояние 03', это будет центр верхнего торца корпуса, проецирующегося тоже в эллипс, большая ось которого будет перпендикулярна оси Z1 (рис. 2.7.1, а). Далее, (рис. 2.7.1, б) и соответственно по оси Х1 и Z1 строим внутренние торцы фланцев, с помощью отрезков 14, 25, 36 находим центры искомых эллипсов. И, наконец, пристраиваем цилиндрические патрубки фланцев, примыкающие к сферической части корпуса. Изображаемая деталь требует построения разреза в аксонометрии, который может быть выполнен двумя парами секущих плоскостей: 1-ая пара – фронтальная и профильная плоскости, 2-ая пара – фронтальная и горизонтальная плоскости. Остановимся на первом варианте ( введем плоскости S1 и S2). Плоскость S1 пересекает цилиндрические поверхности фланцев и патрубков по образующим АВ и СD…, а сферическую поверхность по окружностям (эллипсам). Плоскость S2 пересекает сферическую поверхность также по окружностям (эллипсам), а вертикальный патрубок и горизонтальный фланец по образующим (рис. 2.7.1). 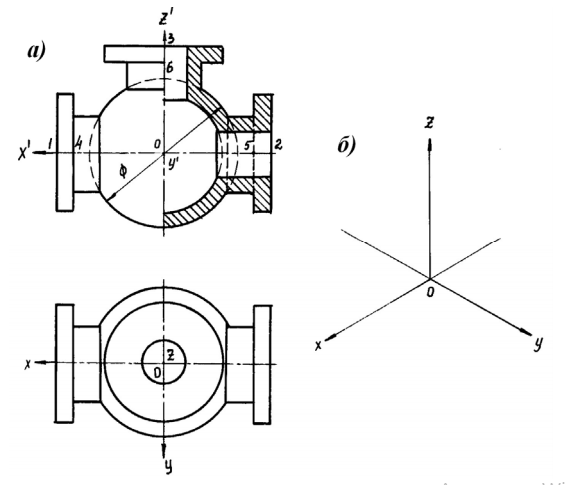 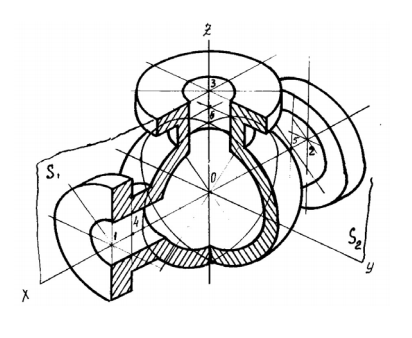 Рис.2.7.1 Завершающий этап построения аксонометрического изображения заключается в следующем: а) убираем с чертежа все дополнительные построения, б) производим обводку линий видимого контура, в) выполняем штриховку в сечениях. 2.8 Последовательность построения аксонометрических проекций предмета. Можно рекомендовать два варианта последовательности построения аксонометрических проекций объектов: 1. построение фигур сечения предмета плоскостями, параллельными координатным плоскостям, с последующим дополнением до полного аксонометрического изображения предмета (рис. 2.8.1); 2. построение аксонометрии всего предмета с последующим выполнением разрезов плоскостями, параллельными координатным плоскостям. Первый способ более предпочтителен, так как освобождает чертеж от лишних линий. В любом случае процесс построения целесообразно разбить на два этапа. Первый этап – подготовительный: 1) прочитать заданный чертеж; 2) выбрать вид аксонометрической проекции; 3) определить, какие разрезы необходимо выполнить, чтобы выявить внутреннее строение предмета (секущие плоскости должны быть параллельны координатным плоскостям x'0'z' и y'0'z'); 4) определить очередность построения изображений поверхностей, ограничивающих предмет. 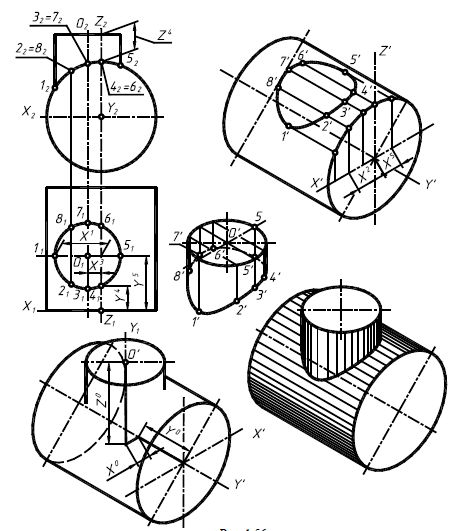 Рис. 2.8.1 Второй этап – графический (см. рис. 2.8.2); 1) отнести данный предмет к декартовой системе координат с нанесением на комплексном чертеже детали проекций координатных осей (рис. 2.8.2, а); 2) построить аксонометрические оси и аксонометрические проекции сечений координатными плоскостями x'0'z' и y'0'z'); одновременно нанести аксонометрические проекции центров всех окружностей (рис. 2.8.2, б); 3) построить эллипсы, являющиеся проекциями окружностей оснований цилиндров и кону- сов, ограничивающих отдельные части детали (рис. 2.8.2, в); 4) построить прямолинейные участки и обвести линии видимого контура детали (рис. 2.8.2, г); 5) удалить вспомогательные линии построения, выполнить штриховку и окончательно обвести чертеж. 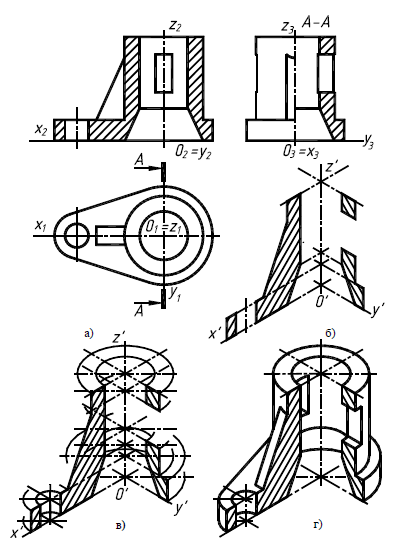 Рис. 2.8.2 2.9 Построение детали в фронтальной диметрической и изометрической проекциях. Построение фронтальной диметрической и изометрической проекций. Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 2.9.1. 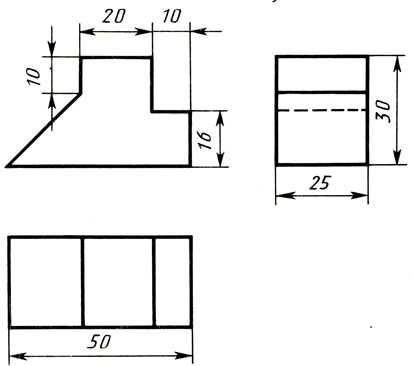 Рис. 2.9.1 Порядок построения проекций следующий (рис. 2.9.2): 1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты - вдоль оси z, длины - вдоль оси х (рис. 2.9.2, а). 2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной ди-метрической проекции - сокращенную в 2 раза; для изометрии - действительную (рис. 2.9.2, б). 3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 2.9.2, в). 4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 2.9.2, г). 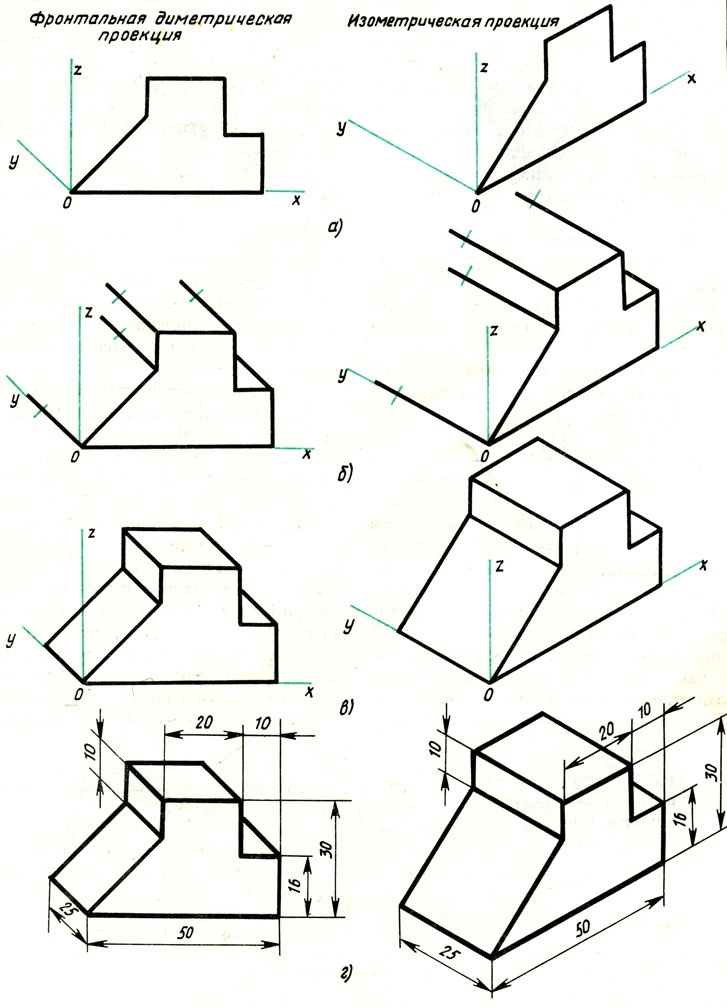 Рис. 2.9.2. Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у. В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально. Построение аксонометрической проекции квадрата показано на рис. 2.9.3, а и б. Вдоль оси х откладывают сторону квадрата а, вдоль оси у - половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми. 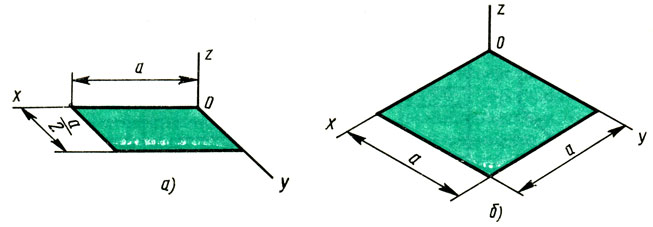 Рис. 2.9.3. Построение аксонометрической проекции треугольника показано на рис. 2.9.4, а и б. Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у - его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых. 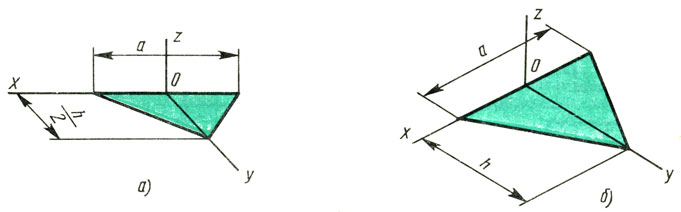 Рис. 2.9.4. Построение аксонометрической проекции правильного шестиугольника показано на рис. 2.9.5. По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых. 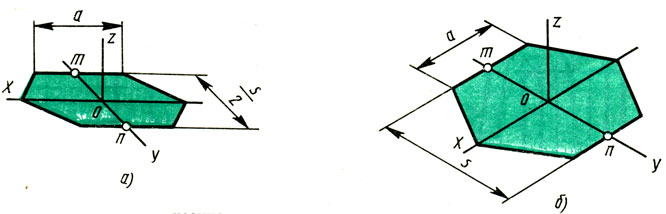 Рис. 2.9.5.
Согласно ГОСТ 2.317-68 ЕСКД линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям. Рис. 2.10.1, а – штриховка в изометрии, рис. 2.10.1, б – штриховка в диметрии. 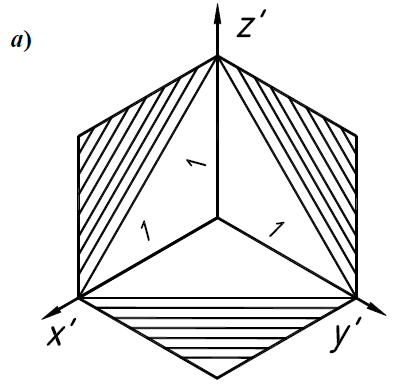 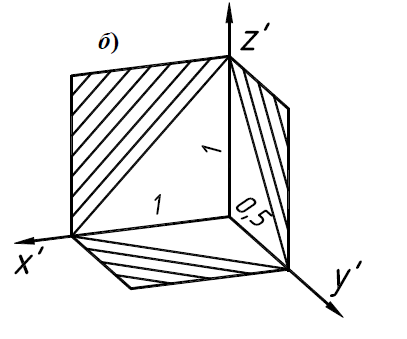 Рис. 2.10.1 При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии – параллельно измеряемому отрезку. В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют. |
