Лекция №6_Минимизация ФАЛ. Лекция 6 Минимизация комбинационных логических устройств
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Лекция №6 Минимизация комбинационных логических устройств Описание ФАЛ в виде последовательности десятичных или двоичных чисел. Описание ФАЛ в виде кубических комплексов Теорема поглощения и теорема склеивания – основные теоремы минимизации ФАЛ Минимизация ФАЛ методом Квайна Минимизация ФАЛ методом кубических форм Минимизация ФАЛ методом карт Карно (Вейча) Описание ФАЛ в виде последовательности десятичных или двоичных чисел. Описание ФАЛ в виде кубических комплексов ФАЛ КЛС. ФАЛ, выраженные в СДНФ и СКНФ, описывают алгоритм работы КЛС, которые могут быть созданы на любой базисной комбинации элементарных логических элементов. Как правило, КЛС, созданные с использованием СДНФ и СКНФ, обладают аппаратной избыточностью. Поэтому при проектировании КЛС с целью минимизации (упрощения) логических функций используют методов: А) метод Квайна; Б) метод кубических форм; В) метод карт Карно (картВейча) ; Г) метод Мак-Класки - специальный алгоритмически метод минимизации на ЭВМ. Способы описания ФАЛ: а) словесное описание;
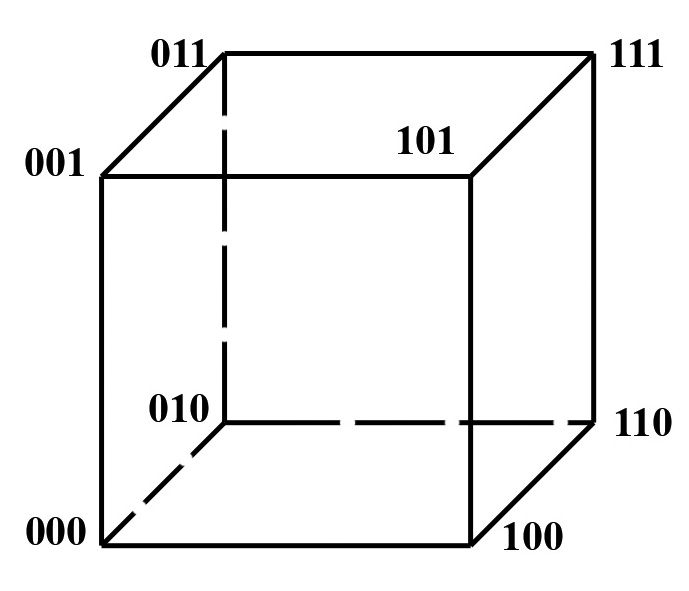
в) в виде алгебраического выражения: ДНФ, КНФ, СДНФ,СКНФ; г) описание в виде последовательности десятичных или двоичных чисел: y(x3,x2,x1,x0)=Σ(4,5,6,9)=V(4,5,6,9)= V(0100,0101,0110,1001); y=(x3,x2,x1,x0)=П(2,3,7,5)=∩(2,3,7,5); д) представление в виде кубических комплексов:
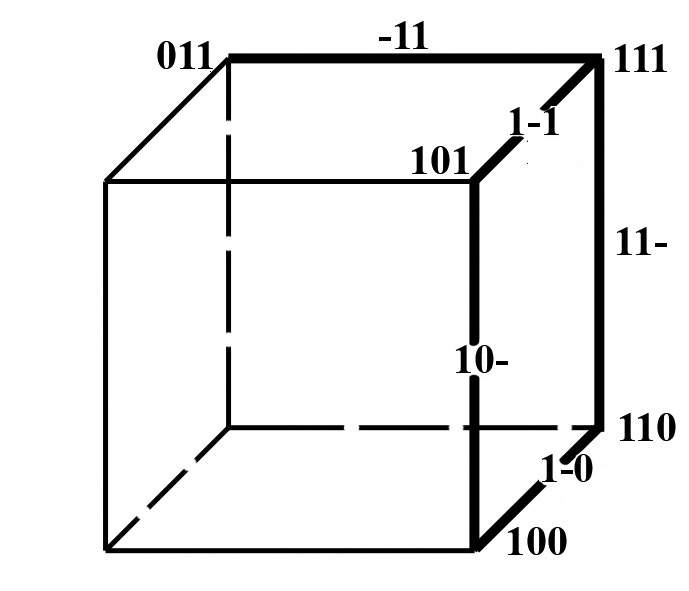
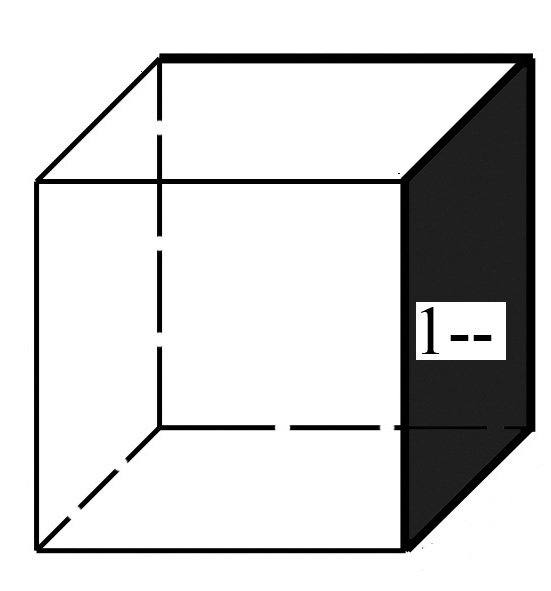
y(x2,x1,x0)= Σ(3,4,5,6,7)=V(011,100,101,110,111); Кубы, отличающиеся только одной переменной, называются соседними. Ранг куба определяется числом несовпадающих переменных координат – числом прочерков. 1.4 Нулевой кубический комплекс K0 - множество “0”кубов: К0= Σ(011,100,101,110,111) 1.5 Единичный кубический комплекс К1- множество единичных кубов: К1= Σ(-11,10-,1-0,11-,1-1): 1.6 Двоичный кубический комплекс К2- множество двоичных кубов: К2= Σ(1- -) 1.7. Кубический комплекс К(Z) образуется сложением кубических комплексов К0,К1,…,Кn-1 Кубический комплекс К(Z) для нашего примера: K(Z)=(011,100,101,110,111,-11,11-,1-1,10-,1-0,1- -) 1.8 Покрытием П(Z) называют подмножество кубов из комплекса К(Z) разных рангов. 1.9 Цена любого n-куба ранга r, входящего в П(Z),равна: Цk=(n-r)k n-число переменных куба; r-ранг куба. 1.10 Цена покрытия П(Z) равна: Теорема поглощения и теорема склеивания – основные теоремы минимизации ФАЛ 2.1.Теорема поглощения: (x0x1+x1)=(x0+1)x1=x1; (KX0+K)=K, (x1+x0)x1=x1x1+x0x1=x1x0+x1=x1; (K+X0)K=K. 2.2. Теорема склеивания: Действительно: 3. Минимизация ФАЛ методом Квайна. 3.1 Минимизируемая функция представляется в СДНФ и к ней применяются все возможные операции неполного склеивания: 1) 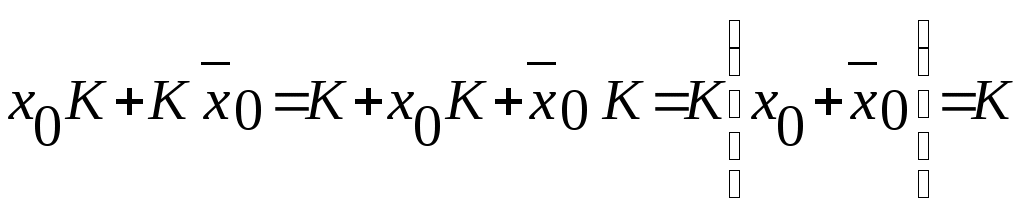 а затем поглощения: 2) K+KX0=K(1+ X0)=K, где 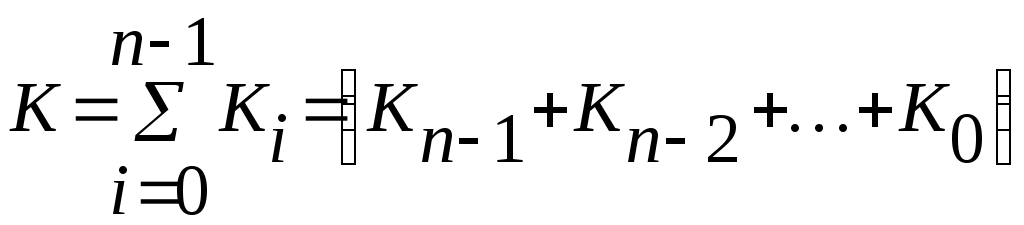 3.2 Эта пара операций может применяться многократно: y= (x2,x1,x0)= Σ(3,4,5,6,7)=V(011,100,101,110,111)  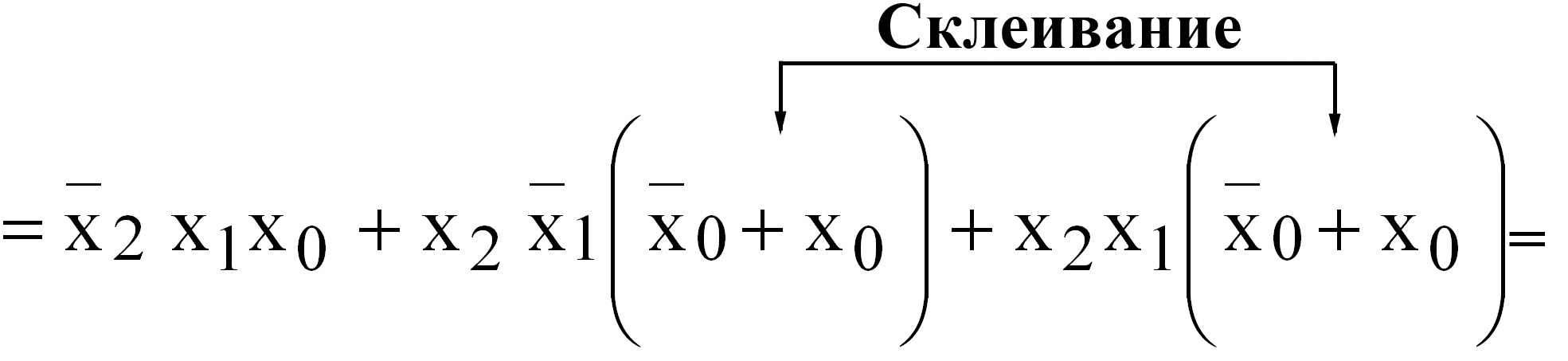 4 Минимизация ФАЛ методом кубических форм. 4.1. 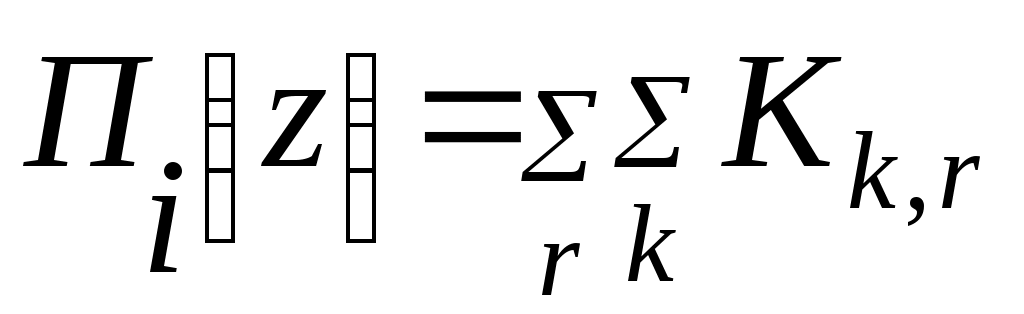 Мы условились, что цена i-го покрытия равна сумме покрытий каждого куба : Цi= ΣЦk= Σ(n-r)k, где – Цk=(n-r)k - цена k-куба, входящего в покрытие ; n - число переменных куба; r- ранг куба. 4.2 Суть минимизации ФАЛ сводится к поиску покрытия П(Z) кубического комплекса К(Z), имеющего минимальную цену Цn= ΣЦkmin . 4.3. Покрытие П(Z) комплекса К(Z), имеющее минимальную цену, называется покрытием Квайна, а соответствующая этому покрытия ДНФ называется минимальной ДНФ (МДНФ). Пример: K(Z)=(011,100,101,110,111,-11,11-,1-1,10-,1-0,1- -); П1(Z)=(011,100,101,110,11)=K0; П2(Z)=(-11,11-,1-1,10-,1-0)=K1; Перебирая сочетания кубов различных рангов можно получить следующее покрытия П3(Z)=(011,11-,10-)=K2 , П4(Z)=(-11,1-1,1-0)=K3, П5(Z)=(011,1- -)=K4 , Цn= 3+1=4; П6(Z)=(-11,1- -) и т.д. Цn= 2+1=3. Соответствующие ДНФ имеют Покрытие , имеющее минимальную цену, называется покрытием Квайна, а соответствующая этому покрытию ДНФ - МДНФ. Минимизация ФАЛ методом карт Карно (Вейча) 5.1. Карта Вейча – прямоугольная таблица, число клеток в которой для ФАЛ n-переменных равно 2ⁿ. Каждой из клеток поставлен в соответствие некоторый набор входных переменных, причем рядом расположенным клеткам соответствуют соседние наборы входных переменных (кодов), а в самих клетках записаны значения функции, определенные для этих кодов. Карты Карно – это графическое двухкоординатное представление таблиц истинности ( матричное представление). По осям располагают значения (наборы) входных переменных, а значения логических функций – в ячейках (клетках), расположенных на пересечении строк и столбцов. 5.2 Карта Карно двух переменных :     1  0    5.3 Карта Карно трех переменных : 01 11 10 00        1   0   «Цилиндр» Крайние столбцы являются соседними. Нижние и верхние строки – соседние. 5.4 Карта Карно 4-х переменных :  01 01       10  11  01   00 00 «Тор» Крайние столбцы являются соседними. Нижняя и верхняя строки – соседние. 5.5 Рассмотрим пример: : 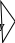    Д   0 0      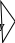 У УД   1 1    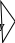   Д2       
5.6 Карта Карно будет следующей: 00 01 11 10  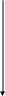       Для реализации КЛС потребуется 3 элемента НЕ, 4 элемента И на три входа и 1 элемент ИЛИ. 5.7 Два метода минимизации булевых выражений по картам Карно: метод минимальных сумм; метод минимальных произведений; 5.8 Метод минимальных сумм заключается в следующем: в карте Карно рассматриваются только ячейки, содержащие 1; ячейки, содержащие 1, объединяются в группы размером Для каждой группы отбираются те переменные на координатных осях, значения которых не изменяются в пределах группы. Эти переменные и будут входить в произведение минимальной суммы. Если переменные равны логическому нулю, то они должны входить с отрицанием, если они равны логической единице – без отрицания. 4.Пример для четырех переменных а 00 01 11 10             0  0 1 0 1 1 0 1 0 1 1   01 1 0 1 1 b   1  1 1 1 0 0 1 1 1 0 0  1  0 1 0 0 0 0 1 0 0 0 Рисунок - Карта Карно для четырех переменных с Для четырех переменных минимизация приводит почти к трехкратной экономии ЛЭ. В карте можно выделить три группы: Для группы a согласно описанным выше правилам можно записать произведение вида: т.к. x1 и x2 меняют свои значения от строки к строке, а x3 и x4 не изменяются в пределах группы ( одного столбца но изменяют значения «0», поэтому вошли в произведение с отрицанием.) Таким же образом для групп b и c можно записать: Минимальная сумма для рассматриваемой карты будет выглядеть следующим образом: т.е.содержит меньшее число произведений, чем в обычной ДНФ для данной карты Карно ( в виде ДНФ функции У содержала бы 9 произведений – 3х кратная избыточность в построении КЛС) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||