Понятие нормы вектора и матрицы. Свойства норм.. Лекция 7 финал. Лекция 7 Тема. Понятие нормы вектора и матрицы. Свойства норм
 Скачать 42.31 Kb. Скачать 42.31 Kb.
|
|
Лекция №7 Тема. Понятие нормы вектора и матрицы. Свойства норм. При изучении итерационных процессов решения СПАУ нам понадобятся понятия норм векторов и матриц. Будем обозначать норму вектора 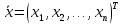 через через  . Согласованная с ним норма матрицы . Согласованная с ним норма матрицы  определяется по формуле: определяется по формуле: Наиболее употребительными являются следующие нормы: 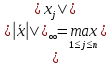 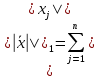 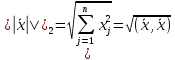 Согласованными с ними нормами для матриц являются, соответственно, следующие нормы: 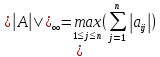 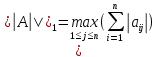  , здесь , здесь 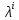 – собственные вектора матрицы – собственные вектора матрицы 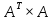 . .Свойства норм векторов и матриц:  при при  – нулевая матрица – нулевая матрица при при  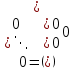 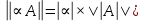 , где , где 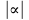 - модуль числа - модуль числа 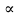 . .  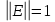 , где E – единичная матрица , где E – единичная матрица  Пример  Ответ: Ответ:    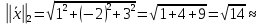 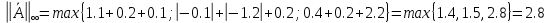  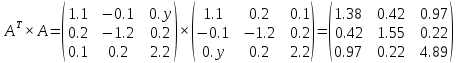   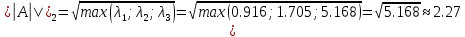 Тема. Решение СЛАУ методом простой итерации. Запишем систему линейных алгебраических уравнений в компактном виде:  , (*) , (*)где      . .Добавим к обеим частям уравнения (*) по вектору x: 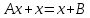 и перепишем новое уравнениев таком виде: 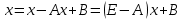 , где , где  – единичная матрица. – единичная матрица.Введём обозначение  , тогда СЛАУ перепишется в таком виде , тогда СЛАУ перепишется в таком виде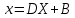 Последовательность вычислений 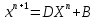 (**) (**)называется методом простых итераций. Пример:  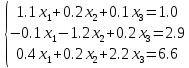 Сделаем предварительные преобразования СЛАУ таким образом, чтобы элементы матрицы А стоящие на главной диагонали были близки к единице: 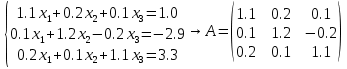 Здесь второе уравнение умножается на -1; Третье уравнение разделяется на 2. Тогда матрица D будет иметь вид: 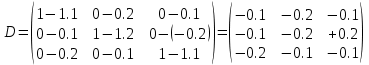 В развернутом виде последовательность вычислений 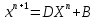 будет выглядеть так: будет выглядеть так: 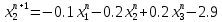 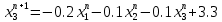 Если последовательность 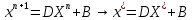 сходится к неподвижной точке x* при  то эта точка (вектор x*) и является решением исходного уравнения AX = B. то эта точка (вектор x*) и является решением исходного уравнения AX = B.Возникает ряд вопросов: Какие требования нужно предъявить к D и x0, чтобы последовательность xn сходилась к x* решению СЛАУ Ax = B? С какой скоростью сходится этот процесс, т.е. каков закон убывания абсолютных погрешностей, получаемых по формуле (**) приближения? Сколько нужно сделать итераций, чтобы при заданном начальном приближении x0 найти решение задачи с заданной точностью? Теория. Пусть  . Тогда при любом начальном векторе x0 метод простых итераций сходится к единственному решению x* и при всех . Тогда при любом начальном векторе x0 метод простых итераций сходится к единственному решению x* и при всех 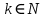 (N – натуральный ряд чисел (N – натуральный ряд чисел 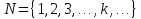 ) справедлива оценка погрешности: ) справедлива оценка погрешности: (апостериорная). (апостериорная). (априорная). (априорная).Априорная оценка – оценка до начала счёта. Апостериорная оценка – оценка после проведения «k» итераций. Доказательство: Можно из равенств:  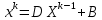 записать их разницу:  . .Из свойств норм матриц и векторов: 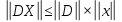 можно получить (с учётом  ) следующее неравенство: ) следующее неравенство: 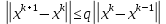 С учётом этого свойства запишем следующую цепочку неравенств: 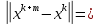 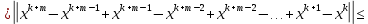  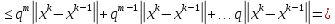 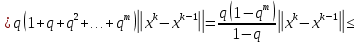 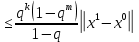 (Здесь записана сумма геометрической прогрессии) (Здесь записана сумма геометрической прогрессии)Отсюда следует, что последовательность x1, x2, …, xk, … является фундаментальной в пространстве Rn и сходится у некоторой точке (вектору) x*. Переходя к пределу в равенстве  получим получим 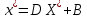 . .Очевидно, что x* является единственным решением, т.е. предположив существование другого решения из условия 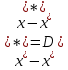 приходим к противоречию приходим к противоречию  . .Тема. Метод Якоби решения СЛАУ. Пусть имеется СЛАУ: 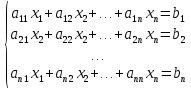 где на диагонали все 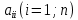 отличны от нуля (в противном случае всегда можно поменять местами уравнения так, чтобы все отличны от нуля (в противном случае всегда можно поменять местами уравнения так, чтобы все  ). ).Преобразуем данную СЛАУ к следующему виду: 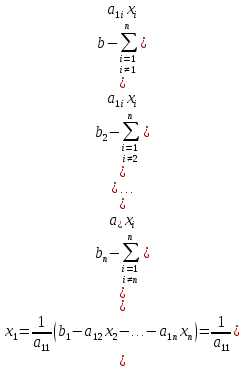 или в общем виде:  в матричном виде:  где   Здесь на диагонали стоят пули. Теорема. В случае диагонального преобладания матрицы А в СЛАУ метод Якоби сходится. Доказательство: т.к.  то  или для нормы или для нормы  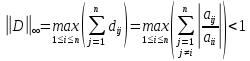 Следовательно, по предыдущей теореме итерационный процесс  сходится. Тема. Итерационный метод Зейделя решения СЛАУ Перепишем СЛАУ уравнений: 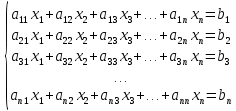 Здесь, как и раньше, предполагается, что 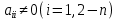 в следующем виде: в следующем виде: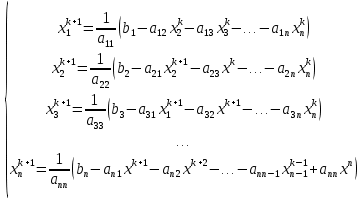 или в компактном виде: 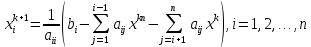 В матричном виде эта СЛАУ может быть записана в следующей форме: 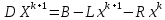 (*) (*)где  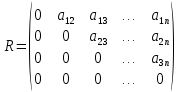 D – Диагональная матрица. L – Матрица нижнего треугольного заполнения. R – Матрица верхнего треугольного заполнения. Перепишем СЛАУ в следующем матричном виде  или или  . .Введём новые обозначения 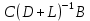 и и  тогда  |
