лекция 9. Лекция 9 Тема Геодезические работы при съемке больших территорий тема 1
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Лекция № 9 Тема 1.4. Геодезические работы при съемке больших территорий. тема 1. Организация геодезических работ при съемках больших территорий. План. Общие сведения о съемках больших территорий и применение их для целей землеустройства и кадастра. Организация геодезических работ. Государственная геодезическая сеть. Понятие о картографических проекциях. Проекция Гаусса. Шестиградусные и трехградусные зоны. Определение прямоугольных координат рамок трапеций. Литература: Маслов А.В. Геодезия. Маслов А.В. Гладилина Е.Ф. Костык В.А. Геодезия. Общие сведения о съемках больших территорий и применение их для целей землеустройства и кадастра. Одной из основных задач практической геодезии является съемка местности – комплекс полевых и камеральных работ, в результате которых получается план или карта. Все съемочные работы, выполняемые в поле (на земле, под землей, над землей), называются полевыми, а все вычислительные и графические работы, выполняемые в кабинетах или лабораториях – камеральными. Если в результате съемки создается план или карта без изображения рельефа, то съемка называется горизонтальной (ситуационной); если же изображается и ситуация и рельеф, то съемка называется топографической. По способу выполнения съемки местности подразделяются на наземные, дистанционные и комбинированные. Наземные съемки делятся на: плановую (горизонтальную); высотную (вертикальную); планово-высотную (комбинированную). Дистанционные съемки делятся на аэросъемку и космическую съемку, обе из которых бывают фотографические и нефотографические. Комбинированная съемка является комбинацией дистанционной и наземной съемок. Плановая ситуация рисуется по аэроснимкам, а рельеф снимают на фотоплан в полевых условиях. Аэрофотосъемка и комбинированная съемка являются основными методами создания карт и планов на большие территории. Наземную съемку применяют при создании крупномасштабных планов небольших участков, когда применение аэрофотосъемки либо невозможно, либо экономически невыгодно. Съемки различают по видам применяемых приборов. Теодолитная съемка выполняется теодолитом и мерной лентой. В результате получают контурный или ситуационный план (горизонтальная съемка). Применяют на равнинной местности, при съемке населенных пунктов, в сельском и лесном хозяйстве. Фототеодолитная съемка выполняется с помощью фототеодолита, а камеральная обработка и рисовка плана выполняется на стереоприборах. Применяют в горной местности. Нивелирование поверхности выполняется с помощью нивелира и рейки. По результатам съемки вычерчивается план местности, на котором рельеф изображен точно, а изображение ситуации либо отсутствует, либо выполнено с невысокой точностью. Это один из простых и точных видов съемки, применяемый при планировке аэродромов, стадионов, стройплощадок и т.д., где требуется подсчет объемов земляных работ. Нивелирование трассы – это съемка узкой полосы местности, по оси которой проложен теодолитный ход. По результатам съемки строят профиль трассы. Тахеометрическая съемка выполняется с помощью тахеометра, получают план с изображением рельефа. Применяют на пересеченной местности, особенно при изыскании линейных сооружений, при съемке малых строительных площадок. Мензульная съемка выполняется с помощью мензулы и кипрегеля. В результате съемки непосредственно на местности получают план с изображением рельефа. Буссольная съемка выполняется с помощью буссоли и как самостоятельную применяют лишь при съемке небольших лесных участков, а также в качестве дополнительной при других видах съемок. Глазомерная съемка(рекогносцировка) может производиться для предварительного ознакомления с местностью. Чтобы обеспечить равную высокую точность измерений на обширных территориях в геодезии действует принцип работы: от общего к частному. Прежде создается геодезическая опорная сеть пунктов, геодезическая основа, а затем выполняется съемка подробностей. Геодезическая сеть – это система обозначенных на месте пунктов с вычисленными для них координатами (X,Y,H). Во избежание грубых ошибок действует второй принцип геодезических работ: постоянный поэтапный контроль измерений и вычислений (ни шагу вперед, пока не проверено предыдущее измерение или вычисление). Основные этапы съемок. 1. Подготовительные работы: получение задания, изучение существующего картографического материала, наличия пунктов ГГС. 2. Рекогносцировка местности – изучение местности, выбор местоположения точек съемочного обоснования (точек хода). 3. Полевые работы: измерение углов, длин линий, привязка хода, съемка ситуации. 4. Камеральные работы: вычислительная обработка всех полевых измерений, вычерчивание плана местности. 5. Оформление материалов. Подготовка их к сдаче. Государственная геодезическая сеть. Выполнение всех геодезических измерений сводится к определению взаимного положения точек на земной поверхности. Измерения сопровождаются погрешностями, которые накапливаются по мере удаления съемки от начальной точки. Для уменьшения погрешностей и для более равномерного их распределения по территории съемку производят с точек съемочного обоснования, так называемых опорных геодезических пунктов. Плановое положение геодезических пунктов определено в единой системе координат, а высотное – в единой системе высот. Система геодезических пунктов с известными координатами равномерно размещенная по территории, образует опорную геодезическую сеть. Согласно принципу перехода «от общего к частному» вся опорная сеть подразделяется на классы, и ее построение осуществляется несколькими ступенями: от сетей высшего класса к низшему, от крупных и точных геометрических построений к более мелким и менее точным. Пункты высших классов располагаются на больших расстояниях друг от друга и затем последовательно сгущаются путем развития между ними сетей более низких классов. Такой подход позволяет в сжатые сроки с высокой точностью распространить единую систему координат на всю территорию страны. Геодезические сети России принято подразделять на государственную геодезическую сеть (ГГС), геодезические сети сгущения (ГСС) и съемочные геодезические сети (съемочное обоснование). Государственная геодезическая сеть (ГГС) является главной геодезической основой топографических съемок всех масштабов, она включает в себя плановые и высотные геодезические сети. В плановых геодезических сетях для каждого пункта определяются прямоугольные координаты в общегосударственной системе. Плановые сети подразделяются на 1, 2, 3 и 4 класс, различающиеся между собой точностью угловых и линейных измерений, длиной сторон сетей и порядком их последовательного развития. Сеть 1 класса (высшей точности) охватывает всю территорию страны как единое целое. Сеть каждого последующего класса строится на основе сетей высших классов. Плановые сети создаются методами триангуляции, трилатерации, полигонометрии и их сочетаниями. Триангуляция – метод определения взаимного планового положения геодезических пунктов путем построения на местности системы смежно- расположенных треугольников, в которых измеряют все углы, а в сети – длины нескольких базисных сторон (рис.25а). Длины других сторон треугольников рассчитываются по формулам тригонометрии. Последовательно решая прямую геодезическую задачу, можно рассчитать координаты всех пунктов сети. Триангуляция 1 класса создается в виде астрономо-геодезической сети и призвана обеспечить решение основных научных задач, связанных с определением формы и размеров Земли. Она является главной основой развития сетей последующих классов и служит для распространения единой системы координат на всю территорию Российской Федерации. Ее построение осуществляется с наивысшей точностью, которую могут обеспечить современные приборы при тщательно продуманной методике измерений. Трилатерация – метод определения взаимного планового положения геодезических пунктов путем построение на местности системы смежнорасположенных треугольников, в которых измеряют все стороны (рис.25б). В связи с отсутствием в трилатерации избыточных измерений для обеспечения возможности контроля измерений и повышения их точности путем уравнивания в трилатерации измеряют длины диагоналей, соединяющих вершины смежных треугольников. Поэтому ряды триангуляции состоят из геодезических четырехугольников, центральных систем или их комбинаций. 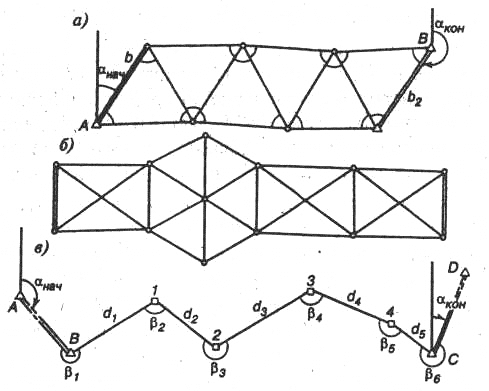 Рис.25. Методы планового обоснования геодезических сетей: а) триангуляция; б) трилатерация; в) полигонометрия. В настоящее время, в связи с широким использованием высокоточной светодальномерной техники метод трилатерации находит все более широкое применение в практике создания геодезических сетей. Полигонометрия – метод определения взаимного планового положения геодезических пунктов путем проложение на местности ломаной линии (полигонометрического хода), или системы линий, в которых измеряют все углы и все стороны (рис.25в). Применение светодальномерной техники открыло широкие возможности для развития метода полигонометрии. Согласно 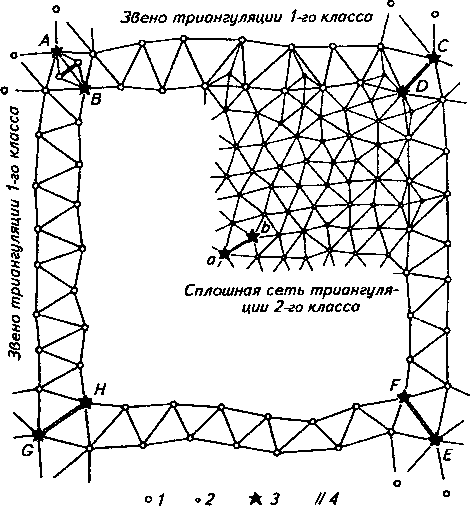 Рис.26. Схема построения плановой ГГС методом триангуляции: 1 – пункт триангуляции 1-го класса; 2 – пункт триангуляции 2-го класса; 3 – пункт Лапласа; 4 – базисная сторона. Инструкции о построении государственной геодезической сети полигонометрия по точности построения приравнивается к триангуляции и может заменять соответствующие классы последней. Как правило, метод полигонометрии целесообразно применять в районах, где триангуляция требует сплошной постройки высоких знаков. Полигонометрия 1 класса строится в виде вытянутых по направлениям меридианов и параллелей ходов, образующих звенья первоклассного полигона с периметром 700–800 км. На концах звена (в вершинах полигонов) определяются пункты Лапласа. Полигонометрия 2 класса развивается внутри полигонов триангуляции или полигонометрии 1 класса в виде сети замкнутых полигонов с периметром 150–180 км. Полигонометрия 3 и 4 классов строится в виде систем ходов с узловыми пунктами или одиночных ходов, опирающихся на пункты государственной геодезической сети высших классов. Высотные (нивелирные) геодезические сети создаются для распространения по всей территории страны единой системы высот. По точности и назначению государственная нивелирная сеть разделяется на сети I, II, III и IV классов. Нивелирные сети I и II классов являются главной высотной основой, посредством которой устанавливается единая (Балтийская) система высот по всей территории России. Линии нивелирования I и II классов прокладываются по заранее разработанным направлениям, с наиболее благоприятными грунтовыми условиями и наименее сложным профилем. Нивелирная сеть I класса состоит из ходов, образующих сомкнутые полигоны периметром около 2000 км. Нивелирование I класса выполняется с наивысшей точностью, достигаемой применением наиболее совершенных приборов и методов наблюдений. Нивелирная сеть II класса опирается на пункты нивелирования I класса и образует полигоны периметром в 500–600 км. Нивелирные сети III класса прокладываются внутри полигонов нивелирования I и II классов в виде систем и отдельных ходов, делящих полигон II класса на 6–9 полигонов периметром 150–200 км. Дальнейшее сгущение нивелирной сети III класса выполняется построением систем ходов нивелирования IV класса, опирающихся на пункты нивелирования высших классов. Ходы нивелирования IV класса являются – непосредственной высотной основой топографических съемок; густота их прокладки обусловливается масштабами съемок и характером рельефа местности. Геодезические сети сгущения (ГCС) развиваются на основе государственной геодезической сети и служат для обоснования крупномасштабных съемок, а также инженерно–геодезических и маркшейдерских работ, выполняемых в городах и поселках, на строительных площадках крупных промышленных объектов, на территориях горных отводов и т. д. Плановые геодезические сети сгущения создаются в виде триангуляции и полигонометрии 1 и 2 разрядов. Триангуляция 1 разряда развивается в виде сетей и цепочек треугольников со стороной 1–5 км, а также путем вставок отдельных пунктов в сеть высшего класса. Триангуляция 2 разряда строится так же, как триангуляция 1 разряда; кроме того, положение пунктов 2 разряда может определяться прямыми, обратными и комбинированными геодезическими засечками. Длины сторон треугольников в сетях 2 разряда принимаются от 0,5 до 3 км. Полигонометрия 1 и 2 разрядов создается в виде одиночных ходов или систем с узловыми точками, длины сторон которых принимаются в среднем равными, соответственно, 0,3 и 0,2 км. В полигонометрии 2 разряда точность угловых и линейных измерений в 2 раза ниже по сравнению с полигонометрией 1 разряда. На все пункты геодезических сетей сгущения должны быть переданы отметки нивелированием IV класса или техническим нивелированием. В горной местности допускается передача отметок точек тригонометрическим нивелированием. Геодезические съемочные сети создаются для сгущения геодезической сети до плотности, обеспечивающей выполнение топографических съемок всех масштабов. Плотность пунктов должна обеспечивать высокое качество съемки. Съемочное обоснование развивается от пунктов государственных геодезических сетей и геодезических сетей сгущения. Съемочные сети создаются построением съемочных триангуляционных сетей, продолжением теодолитных, тахеометрических и мензульных ходов, прямыми, обратными и комбинированными засечками. При развитии съемочного обоснования одновременно определяется, как правило, плановое и высотное положение точек. Высоты точек съемочных сетей определяются тригонометрическим геометрическим нивелированием. Для обозначения плановых геодезических пунктов и их закрепления на местности служат подземные центры и наземные сооружения, т.н. геодезические знаки. Подземные центры должны обеспечивать неизменность положения и сохранность пункта в течение продолжительного времени. Типы центров установлены соответствующими инструкциями применительно к климатическим и физико-географическим условиям региона и местным особенностям. Над центрами сооружают деревянные или металлические наружные знаки, которые служат визирными целями при измерении углов и линий. Наружные знаки бывают разных конструкций в зависимости от условий местности и расстояния между пунктами. Пункты высотной геодезической сети закрепляются грунтовыми реперами, стенными реперами и марками. Для закрепления пунктов съемочного обоснования, сохранность которых должна быть обеспечена в течение нескольких лет, применяются центры в виде бетонных и деревянных столбов и металлических труб. Большая часть пунктов съемочных сетей закрепляется временными знаками, представляющими собой деревянные колья или металлические трубки. Для облегчения отыскания такого знака рядом с ним забивают сторожок. Завершением работ по созданию ГГС является составление каталогов, где указывают названия и описание местоположения каждого пункта, класс сети, тип знака, год постройки, координаты Х,У,Н и др. Понятие о картографических проекциях. Проекция Гаусса. Шестиградусные и трехградусные зоны. Картографическая проекция – это определенный способ отображения одной поверхности на другую, устанавливающий аналитическую зависимость между координатами точек эллипсоида (сферы) и соответствующих точек плоскости. Как известно, положение любой точки на поверхности Земли определяется ее географическими координатами—широтой (φ) и долготой (λ). В более общем случае положение точки на земной поверхности может быть определено и в других системах координат — горизонтной, полярной, прямоугольной и т. д.Положение точки на карте, являющейся изображением сферической (сфероидической) поверхности Земли, также должно определяться пересечением двух координатных линий, которые однозначно соответствовали бы координатным линиям на земной поверхности. Иначе говоря, при изображении сферической поверхности на плоскости необходимо, чтобы каждой точке на поверхности сферы однозначно соответствовала бы точка плоскости, являющаяся ее изображением. При этом непрерывной линии перемещения некоторой точки A0 на сфере должна соответствовать непрерывная линия перемещения ее изображения (точки А) на плоскости карты. Способ условного изображения поверхности сферы (эллипсоида) на плоскости называют картографической проекцией. В более узком смысле картографическая проекция — это способ условного изображения на плоскости координатной сетки, соответствующей координатным линиям шара или эллипсоида. Таким образом, сущность всякой картографической проекции состоит в том, что положение любой точки сферической поверхности с координатами φ и λ определяется на плоскости карты картографическими координатами x и y: x = f1(φ , λ)y = f2 (φ , λ)Значения функций f1и f2 находятся, исходя из поставленных условий. Законов изображения поверхности эллипсоида на плоскости может быть бесчисленное множество; очевидно, каждый закон изображения определяется видом функций f1 и f2 в приведенных уравнениях.Положение пунктов геодезических сетей на больших территориях определяют географическими (угловыми) координатами - широтой и долготой, а на малых - прямоугольными (линейными) координатами. Потому что поверхность эллипсоида невозможно перенести на плоскость без искривлений, строят условные изображения поверхности эллипсоида, основанные на определенных математических законах, названных картографическими проекциями. В зависимости от вида искажений их делят на равновеликие, в которых искажаются все элементы, но сохраняется соотношение площадей фигур, равноугольные, где не искажаются углы, но не сохраняется соотношение площадей, и равнопромежуточные, в которых искажаются и углы, и соотношение площадей. Выбор того или иного вида проекции зависит в основном от назначения создаваемого плана или карты. Для составления топографических карт принята поперечно-цилиндрическая равноугольная проекция Гаусса-Крюгера. Гаусс разработал проекцию в 1825-1830г., а в 1912г. Крюгер вывел рабочие формулы для вычислений в этой проекции. 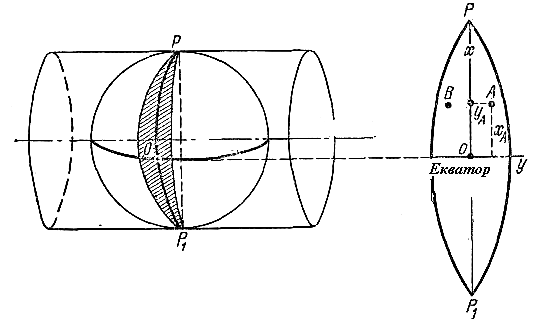 Сущность этой проекции заключается в проектировании точек эллипсоида на поверхность цилиндра. Касание эллипсоида к поверхности цилиндра происходит по среднему (осевому) Меридиану трехградусной или шестиградусной зоны, ограниченной меридианами. Деление поверхности эллипсоида на зоны вызвано тем, что при удалении от осевого меридиана получают значительные искажения положения точек в проекции. Выбор трехградусной или шестиградусной зоны зависит от масштаба создаваемой карты. Так, при создании карт больших масштабов (1:5000 и крупнее) используют трехградусные зоны, а при создании карт масштабов 1:10000 и мельче - шестиградусные. Шестиградусные зоны нумеруют арабскими цифрами, начиная от Гринвичского меридиана, с запада на восток. Долготу осевого меридиана можно вычислить по формуле: Lo = 6°N - 3°, в которой N - номер зоны. Итак, долготы осевых меридианов кратные 3°, но не кратные 6°: 15°, 21°, 27°, 33°, 39°, 45° и т.д. Трехградусные зоны располагаются таким образом, что все предельные и осевые Меридианы шестиградусных зон являются осевыми меридианами трехградусных зон, следовательно, все осевые Меридианы трехградусных зон имеют долготы, кратные 3°. Потому что в зонах после развертывания цилиндра в плоскость осевые меридианы и экватор изображаются взаимно перпендикулярными прямыми, то в каждой из них применяется наиболее простая прямоугольная система координат, где за ось абсцисс приняты осевые меридианы зон, а за ось ордината-экватор. Отрезки ха и уа от точки А до осей координат называют плоскими прямоугольными координатами Гаусса-Крюгера. Потому что наша территория находится в северном полушарии, то абсциссы всех точек будут положительными, а ординаты могут быть и положительными, и отрицательными. Чтобы избежать отрицательных ординат, ось абсцисс смещают на 500 000 м на запад, а для того чтобы определить, в какой из зон находится искомая точка, перед ординатой ставят номер зоны. Например, в зоне 5 точки А и В должны ординаты: уа = +115 672,0м, ув = - 110 432,5м; тогда преобразованные координаты будут на 5 500 000 м больше, т.е. уа = 5 615 672,0м, а ув = 5 389 567,5м. Номенклатура листов топографических карт и планов. Изображение значительной территории в большом масштабе невозможно на одном листе, поэтому крупномасштабные карты составляют на большом количестве листов, ограниченных с севера и юга параллелями, а с запада и востока меридианами. Каждый лист карты представляет собой трапецию географической сетки, построенной по определенной системе, названной разграфкой карты. Карты создают в международной разграфке (номенклатуре), в основе которой лежит лист карты масштаба 1:1000000. Для получения листа этой карты поверхность эллипсоида делят по широте на четырехградусные ряды и по долготе на шестиградусные колонны. Ряды к северу и к югу от экватора обозначают заглавными буквами латинского алфавита, а колонны обозначают арабскими цифрами от 1 до 60, причем счет колонн ведут по направлению с запада на восток от тихоокеанской части Гринвичского меридиана (меридиана с долготой 180°). Колонна 1 лежит между меридианами с длиннотами 180-186° (или 180-174° западной долготы), а между меридианами с 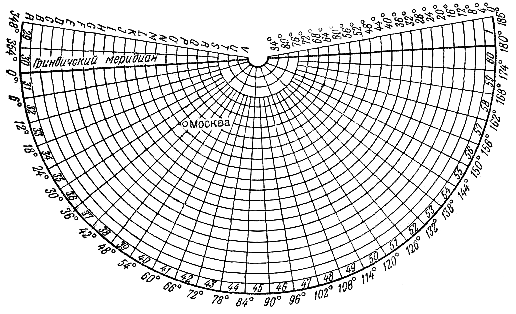 длиннотами 0-6° лежит колонна 31. длиннотами 0-6° лежит колонна 31.Номенклатура карты масштаба 1:1000000 состоит из буквы четырехградусного ряда и номера шестиградусной колонны. Например, лист карты масштаба 1:1000000, на котором находится г.Москва, имеет номенклатуру N-37. Для получения номенклатуры листа карты масштаба 1:500000 лист карты масштаба 1:1000000 делят на четыре части, каждую из которых обозначают первыми заглавными буквами русского алфавита А, Б, В, Г. Размеры их по широте 2° и по долготе 3°. Номенклатура листа карты масштаба 1:500000 обозначается номенклатурой листа карты масштаба 1:1000000, к которой приписывается буква листа масштаба 1:500 000, например, О-36-Г . Чтобы получить номенклатуру листа карты масштаба 1: 200 000, лист карты масштаба 1:1000000 делят на 36 частей, каждая из которых слева направо сказывается римскими цифрами от и до XXXVI. Размеры листов по широте составляют 40', а по долготе 1°. Номенклатура листа карты масштаба 1:200000 будет состоять из номенклатуры листа карты 1:1000000 и номера листа масштаба 1: 200000, например 0-36-ХХШ. Листы карты масштаба 1:100000 получают делением листа карты масштаба 1:1000000 на 144 части с размерами 20' по широте и 30' по долготе, каждая из которых обозначается по порядку арабскими цифрами от 1 до 144 слева направо. Номенклатура их состоит из номенклатуры листа карты 1:1000000 и номера листа карты 1:100 000, например, 0-36-1. 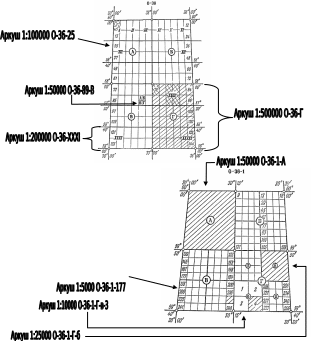 Номенклатура листа карты масштаба 1:100000 является исходной для получения номенклатуры листов масштабов 1:50000, 1:25000, 1:10000, 1:5000, 1:2000. Листы карты масштаба 1:5000 получают делением листа карты масштаба 1:100000 на 256 частей и обозначают арабскими цифрами. Лист карты масштаба 1:5000 включает в себя 9 листов карты масштаба 1: 2000, и их обозначают строчными буквами от "а" до "и". Определение прямоугольных координат рамок трапеций. Для определения прямоугольных координат на каждом листе карты построена координатная сетка в виде квадратов со сторонами, соответствующими 1км на земной поверхности. Таким образом, размеры квадратов на карте зависят от масштаба карты. Топографические карты в создаются только в проекции Гаусса — Крюгера, поэтому вертикальные линии сетки прямоугольных координат (абсциссы) параллельны осевому меридиану, горизонтальные — экватору. Координаты сетки подписаны между внешней и внутренней рамками карты (см.рис.). 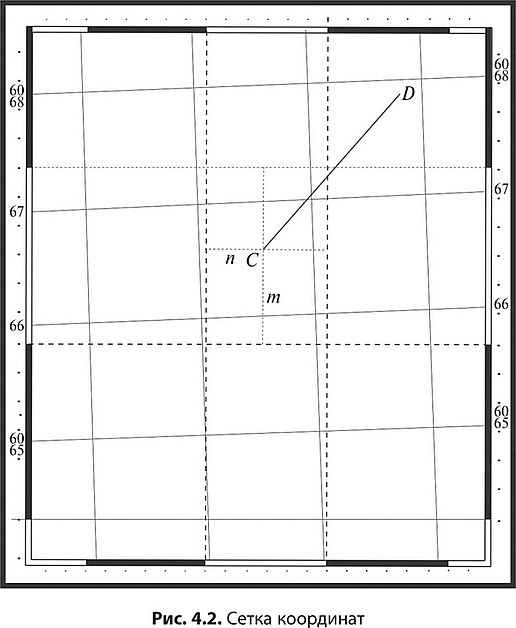 Кроме того, координаты некоторых вершин квадратов подписаны непосредственно на картографическом изображении. На планах размеры квадратов не зависят от масштаба и всегда равны 10см. Координаты сетки квадратов подписаны только между внешней и внутренней рамками. Определение координат сводится к измерению расстояний (приращений координат) и выполняется следующим образом. Вначале из определяемой точки опускают перпендикуляры и на южную и западную стороны квадрата, в котором располагается определяемая точка. Затем с помощью масштабной линейки и циркуля-измерителя определяются длины указанных перпендикуляров. При этом значения приращений координат должны измеряться с точностью масштаба используемой карты или плана. Пусть, например, нужно: 1. Определить прямоугольные координаты точки на карте (рис. 27). Например, точки В. Для этого надо: записать X - оцифровку нижней километровой линии квадрата, в котором находится точка В, т.е. 6657км; измерить по перпендикуляру расстояние от нижней километровой линии квадрата до точки В и, пользуясь линейным масштабом карты, определить величину этого отрезка в метрах; сложить измеренную величину 575м с значением оцифровки нижней километровой линии квадрата: X=6657000+575=6657575м. Определение ординаты Y производят аналогично: записать значение Y - оцифровку левой вертикальной линии квадрата,т.е.7363; измерить по перпендикуляру расстояние от этой линии до точки В, т.е.335м; прибавить измеренное расстояние к значению оцифровки Y левой вертикальной линии квадрата: Y=7363000+335=7363335м. 2.Нанести на карту цель по заданным координатам. Например, точку Г по координатам: Х=6658725 Y=7362360. Для этого надо: найти квадрат, в котором расположена точка Г по значению целых километров, т.е. 5862; отложить от левого нижнего угла квадрата отрезок в масштабе карты, равный разности абсциссы цели и нижней стороны квадрата - 725м; - от полученной точки по перпендикуляру вправо отложить отрезок, равный разности ординат цели и левой стороны квадрата, т.е. 360м. 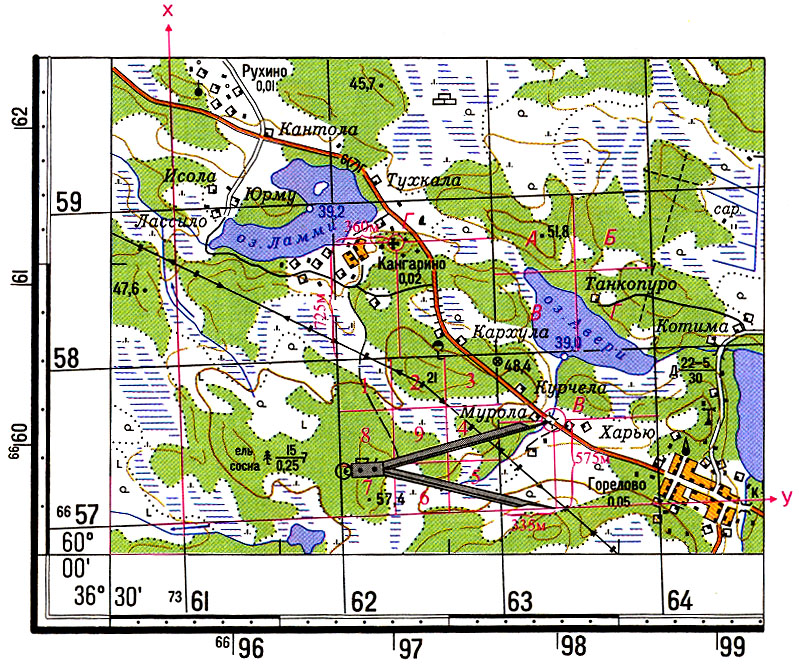 Рис. 27.Определение прямоугольных координат точки по карте (точка В) и нанесение на карту точки по прямоугольных координатам (точка Г) Контрольные вопросы по теме: Для каких целей строят геодезические сети? Какие применяют методы для построения? Что называют координатами Гаусса - Крюгера? Дать понятие картографической проекции. |
