Лекция Электрическое поле заряженных проводников. Энергия электростатического поля
 Скачать 270.5 Kb.
|
|
Семестр 3. Лекция4. Лекция 4. Электрическое поле заряженных проводников. Энергия электростатического поля. Поле вблизи проводника. Электроёмкость проводников и конденсаторов. (Ёмкости плоского, цилиндрического и сферического конденсаторов). Энергия системы неподвижных зарядов. Энергия заряженного проводника, конденсатора. Плотность энергии электростатического поля. П 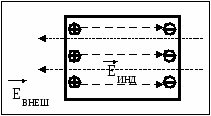 ри внесении проводника во внешнее электрическое поле заряды внутри проводника начинают перемещаться под действием сил со стороны внешнего поля до тех пор, пока не наступит равновесие. Это приводит к перераспределению электрического заряда внутри проводника. Области проводника, до этого электрически нейтральные, приобретают некомпенсированный электрический заряд. Следовательно, в проводнике появляется (или, как говорят, индуцируется) электрическое поле  . 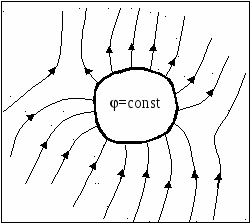Условие равновесия электрических зарядов:  ,т.е. напряжённость поля внутри проводника:  .Следовательно, из равенства  получаем  внутри проводника. Поэтому это условие выполняется и на границе проводника. Т.е. поверхность проводника является эквипотенциальнойповерхностью, поэтому силовые линии электрического поля перпендикулярны поверхности проводника в каждой его точке.Заряженный проводник. Если уединённому проводнику сообщить сторонний электрический заряд, то условие равновесия зарядов опять приводит к условию: , внутри проводника.Отсюда следует, что все сторонние заряды располагаются на поверхности проводника, т.к. напряжённость поля внутри проводника равна нулю, а по теореме Гаусса для любой замкнутой поверхности внутри проводника (в том числе и для наружной поверхности проводника):  .Так как поверхность проводника в этом случае тоже эквипотенциальная, то с 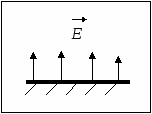 иловые линии электрического поля направлены перпендикулярно поверхности проводника в каждой его точке. Из теоремы Гаусса следует, что вблизи поверхности проводника  - в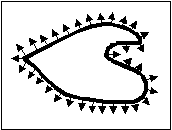еличина вектора электрического смещения равна поверхностной плотности сторонних зарядов.З  аряд по поверхности проводника распределяется таким образом, чтобы потенциал поверхности оставался постоянным. Это приводит к тому, что на поверхности проводника плотность заряда неодинаковая. Например, на острых частях проводников плотность зарядов больше, чем в углублениях. В связи с этим возникают различные явления, например, «стекание заряда». Если проводник находится в воздухе, то вблизи острия происходит ионизация воздуха, уносящая часть электрического заряда – явление, которое называется «электрический ветер».Метод электрических изображений. Если эквипотенциальную поверхность заменить проводящей, после чего отбросить часть поля, которую эта поверхность отделяет, то картина поля в оставшейся части не изменится. И наоборот, если картину поля дополнить фиктивными зарядами так, чтобы проводящую поверхность можно было заменить эквипотенциальной, то начальная картина поля не изменится. П 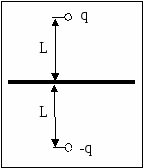 ример. Найдем силу притяжения точечного заряда к бесконечной проводящей плоскости. Для этого дополним картину ещё одним таким же зарядом, но противоположного знака, расположенным симметрично относительно плоскости. Тогда плоскость будет совпадать с эквипотенциальной поверхностью, поэтому плоскость можно отбросить и найти силу взаимодействия между зарядами:  .Энергия заряженного проводника. Энергия уединённого заряженного проводника определяется как энергия системы зарядов:  . На проводнике  , поэтому энергия уединённого проводника: .Для системы заряженных проводников:  .В частности для двух проводников, имеющих одинаковые по величине, но разные по знаку заряды q, энергия будет равна:  .Замечание. Величина разности потенциалов  называется напряжением между телами.Опыт показывает, что между зарядом уединённого проводника и его потенциалом существует линейная зависимость:  . Коэффициент пропорциональности С называется коэффициентом электрической ёмкости или электроёмкостью. Единица измерения электроёмкости – Фарад ( ).Конденсатором называется система из двух проводников, заряженных одинаковыми по величине, но разными по знаку зарядами. Проводники называются обкладками конденсатора. Электроёмкость конденсатора определяется по формуле  .Конденсатор условно обозначается 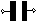 . Соединение конденсаторов Р 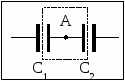 ассмотрим последовательное соединение двух конденсаторов С1 и С2. Точка А между конденсаторами отделена от остальной цепи, поэтому её электрический заряд измениться не может. Так как начальный заряд любой точки был равен нулю, то  . Следовательно, заряды пластин конденсаторов, примыкающих к точке А, равны между собой по величине, но противоположны по знаку. Но так как величина заряда пластин равна заряду конденсаторов, то  . Суммарный заряд точки А равен нулю, поэтому если отбросить эту точку вместе с пластинами, то в схеме ничего не изменится. Т.к. заряды крайних пластин тоже одинаковы по величине, но разные по знаку, то получившийся конденсатор будет иметь такой же по величине заряд. ИТОГ. Заряды последовательно соединённых конденсаторов одинаковы по величине. Общий заряд последовательно соединённых конденсаторов равен заряду каждого из конденсаторов. Для этого случая общее напряжение равно сумме напряжений на конденсаторах: UОБЩ =U1+U2. Заряды конденсаторов одинаковые: q1=q2=q. Тогда  . Поэтому  .При последовательном соединении конденсаторов их ёмкости складываются по закону обратных величин. 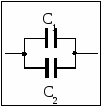 Расчёт ёмкости при параллельном соединении конденсаторов.Для этого случая напряжения на конденсаторах одинаковые: U1=U2=U. Суммарный заряд равен сумме зарядов: qОБЩ=q1+q2 или СОБЩU=C1U+C2U. Тогда СОБЩ =C1+C2 . При параллельном соединении конденсаторов их ёмкости складываются. Энергия конденсатора:  .Суммарный заряд конденсатора равен нулю. Конденсатор накапливает электрическую энергию путём разделения электрических зарядов. Примеры по расчёту ёмкости конденсаторов. Плоский (воздушный) конденсатор представляет собой две параллельные пластины, расстояние между которыми много меньше размеров пластин, так что поле между пластинами можно считать однородным. Между пластинами находится вакуум (воздух), поэтому = 1. 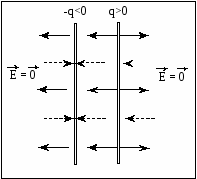 В этом случае при расчёте картины поля можно воспользоваться результатами, полученными для поля бесконечной заряженной плоскости. Так как заряды и площади пластин равны по величине, то и величина напряжённости поля, создаваемого каждой из пластин, одинакова:  , но направления векторов напряжённости разные (вектор напряжённости от отрицательно заряженной пластины показан пунктиром). Между пластинами векторы напряжённости направлены одинаково, поэтому суммарная напряжённость равна сумме напряжённостей полей, созданных каждой из пластин: .Снаружи пластин векторы напряжённости полей направлены противоположно, поэтому напряжённость поля снаружи равна нулю. Таким образом, в конденсаторе напряжённость поля отлична от нуля только между пластинами. Так как электростатическое поле является полем консервативной силы, то интеграл 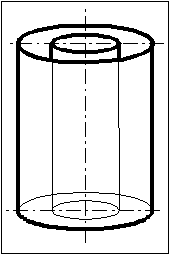 не зависит от формы траектории Г, поэтому разность потенциалов между пластинами м ожно найти вдоль перпендикуляра, соединяющего пластины, длина которого равна d:  , где d – расстояние между пластинами. Тогда электроёмкость плоского (воздушного) конденсатора в соответствии с определением будет равна:  Цилиндрический (воздушный) конденсатор представляет собой два коаксиальных цилиндра одинаковой длины, вложенных друг в друга так, что расстояние между обкладками много меньше размеров обкладок. Пусть длина конденсатора L, заряд внутренней обкладки положительный: q> 0. Радиусы обкладок R1 и R2, пусть R1 < R2. Напряжённость поля между обкладками на расстоянии r от внутренней обкладки, т.е. для R1 <r< R2 , найдём, используя теорему Гаусса:  .Тогда напряжение между обкладками: 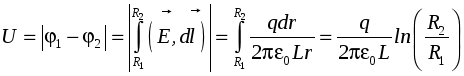 .Поэтому электроёмкость цилиндрического (воздушного) конденсатора: 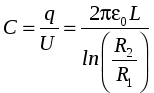 .С 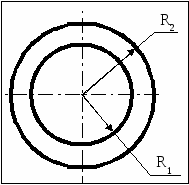 ферический (воздушный) конденсатор представляет собой две вложенные концентрические сферы с радиусами обкладок R1 и R2, R1< R2. Пусть заряд внутренней обкладки q > 0. Напряжённость поля между обкладками на расстоянии r от внутренней обкладки (R1 < r< R2) найдём по теореме Гаусса: .Напряжение между обкладками: 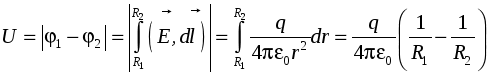 .Поэтому электроёмкость сферического (воздушного) конденсатора 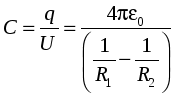 .Объёмная плотность энергии электростатического поля. Рассмотрим плоский воздушный конденсатор. Энергия заряженного конденсатора  .Объём пространства между пластинами конденсатора  . Так как поле между пластинами рассматриваем как однородное, то единица объёма этого поля обладает энергией  . Эта величина  называется объёмной плотностью энергии.В случае, когда поле не является однородным, объёмная плотность энергии  .В веществе объёмная плотность энергии электрического поля  .В случае однородного изотропного диэлектрика  , поэтому  .Т.к.  , то  , где - энергия электрического поля в вакууме,  - энергия поляризации вещества.Пример. Рассмотрим заряженную тонкостенную сферу радиуса R. Так как одноимённые заряды на сфере отталкиваются, то силы отталкивания стремятся растянуть поверхность сферы. Можно считать, что изнутри сферы на стенки действует дополнительное давление р, распирающее сферу и вызванное наличием электрического заряда на поверхности. Найдём р. Напряжённость поля внутри сферы равна нулю, поэтому объёмная плотность энергии электрического поля w отлична от нуля только снаружи сферы. При небольшом увеличении радиуса сферы на dR её объём увеличится, при этом в той части окружающего пространства, которая попала внутрь сферы, объёмная плотность энергии станет равной нулю. Следовательно, изменение энергии поля снаружи будет равно  , где S – площадь поверхности. Но при расширении сферы силы давления внутри сферы совершат работу  . Так как  , то  , откуда  .Пример. Найдем силы, действующие на пластины в заряженном плоском конденсаторе, отключённом от источника питания. Пластины заряжены разноимённо, поэтому они притягиваются. Предположим, что пластины сблизились на малую величину x. Тогда объём конденсатора уменьшился на величину dV = xS, поэтому энергия конденсатора уменьшилась на dW = wdV. Силы притяжения совершат работу A = Fx. Так как A =dW, то Fx = wxS. Поэтому величина силы равна F = wS. Дополнительное давление, которое создают эти силы, равно  .Приведённые примеры показывают, что на тела, находящиеся в электрическом поле, действуют силы, вызывающие дополнительное давление, равное объёмной плотности энергии. Давление, вызванное наличием электрического поля, равно объёмной плотности энергии. Силы, действующие на тела со стороны какого-то поля, называются пондемоторными. |