Лекция Лекция Электрическое поле заряженных проводников. Энергия электростатического поля

• Название: Лекция Лекция Электрическое поле заряженных проводников. Энергия электростатического поля
• Дата: 02.04.2022
• Размер: 117.75 Kb.
• Имя файла: 3sem_lec_04.docx
• Тип: Лекция; #436141

Семестр 3. Лекция 4.

Лекция 4.

Электрическое поле заряженных проводников. Энергия электростатического поля. Поле вблизи поверхности проводника. Электроёмкость проводников и конденсаторов. Ёмко-сти плоского, цилиндрического и сферического конденсаторов. Энергия системы неподвижныхзарядов. Энергия заряженного проводника, конденсатора. Плотность энергии электростати-ческогополя.
При внесении проводника во внешнее электрическое поле, свободные заряды внутри

проводника начинают перемещаться под действием сил со стороны внешнего поля до тех пор, пока не наступит равнове- сие. Это приводит к перераспределению электрического заряда внутри проводника. Области проводника, до этого электриче- ски нейтральные, приобретают некомпенсированный электри-

ческий заряд. Следовательно, в проводнике появляется (или, как говорят, индуцируется) элек-

трическое поле Е_ИНД. Условие равновесия электрических зарядов

→ → → → →

^{F qE}ВНУТР ^{ qE}ВНЕШ ^{ E}ИНД ^{  0}

т.е. напряженность поля внутри проводника

^EВНУТР^{ E}ВНЕШ^{ E}ИНД^{ 0 .}

Следовательно, из равенства

^E_ВНУТР ^{ grad}^_ВНУТР  ^{ 0}

получаем _ВНУТР const

внутри проводника. Следова-

тельно, это условие выполняется и на границе проводни- ка. Поэтому поверхность проводника является эквипо-тенциальной поверхностью и силовые линии электриче- ского поля перпендикулярны поверхности проводника в каждой его точке.

Заряженныйпроводник.

Если уединенному проводнику сообщить сторонний электрический заряд, то условие

равновесия зарядов

F qE_ВНУТР 0

опять приводит к условию

^{EВНУТР grad}^{ВНУТР} ^{ 0 , ВНУТР const}

внутри проводника.

Отсюда следует, что все сторонние заряды располагаются на поверхности проводника, т.к. на- пряжённость поля внутри проводника равна нулю, а по теореме Гаусса для любой замкнутой поверхности внутри проводника (в том числе и для наружной поверхности проводника)

→ →

_{º }D,dS_  q_ВНУТР  0 .

S
Так как поверхность проводника в этом случае тоже эквипотенциаль-ная, то силовые линии электрического поля направлены перпендику- лярно поверхности проводника в каждой его точке.

Из теоремы Гаусса следует, что вблизи поверхности проводника выполняется соотношение D  - величина вектора электрического

смещения равна поверхностной плотности сторонних зарядов.

Заряд по поверхности проводника распределяется таким образом, чтобы потенциал по- верхности оставался постоянным. Это приводит к тому, что на по- верхности проводника плотность заряда не одинаковая. Например, на острых частях проводников плотность зарядов больше, чем в уг- лублениях. В связи с этим возникают различные явления, например,

«стекание заряда»: если проводник находится в воздухе, то вблизи острия происходит ионизация воздуха, уносящая часть электриче-

ского заряда – явление, которое называется «электрический ветер».

Методэлектрических изображений.

Если эквипотенциальную поверхность заменить проводящей, после чего отброситьчасть поля, которую эта поверхность отделяет, то картина поля в оставшейся части не из-менится. И наоборот, если картину поля дополнить фиктивными зарядами так, чтобы прово-дящуюповерхностьможнобылозаменитьэквипотенциальной,тоначальнаякартинаполяне

изменится.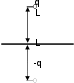

Пример. Найдем силу притяжения точечного заряда к бесконечной про-водящей плоскости. Для этого дополним картину ещё одним таким же зарядом, но противоположного знака, расположенным симметрично от- носительно плоскости. Тогда плоскость будет совпадать с эквипотенци- альной поверхностью, поэтому плоскость можно отбросить и найти силу

взаимодействия между зарядами

F ¹ 4<sub>0

q</sub>2

4L^{2 .}

Энергиязаряженногопроводника.

Энергия уединенного заряженного проводника определяется как энергия системы заря-

₂ i i
дов W ¹ _ q

i
. На проводнике   const, поэтому энергия уединенного проводника

W ¹ _ q  ¹ _ q ¹ q.

₂ i i ₂ i ₂

i i


Для системы заряженных проводников W ¹  q.

₂ k k

k
В частности для двух проводников, имеющих одинаковые по величине, но разные по знаку за-

ряды q: W ¹  q ¹  q   



₂ 1 1 ₂ 2 2 1 2

Замечание. Величина разности потенциалов U ₁  ₂

телами.

называется напряжениеммежду

Опыт показывает, что между зарядом уединённого проводника и его потенциалом суще- ствует линейная зависимость q  C  (при условии   0 на бесконечно большом расстоянии от проводника). Коэффициент пропорциональности С называется коэффициентом электриче- ской ёмкости или электроёмкостью:

C ^q.



Единица измерения электроёмкости – Фарад. Ф = ^Кл .

В

Пример. Найдем ёмкость уединённого проводника имеющего форму сферы радиуса R.

Т.к. потенциал поверхности заряженного сферического проводника равен  

1

4₀

^q, то ём-

R

кость определяется соотношением C ^q 4 R. Исходя из этой формулы можно оценить

_ 0

размеры проводника, ёмкость которого равна 1 Ф: C 1 Ф при

R ¹ 4₀

 9 10⁹
м. Средний ра-

диус планеты Земля

R 6,4 10⁶ м, следовательно, радиус такой сферы больше радиуса Земли

З
примерно в 1400 раз. ♣

Конденсатором называется система из двух проводников, заряженных одинаковыми по величине, но разными по знаку зарядами. Величина заряда одного из проводников называется зарядом конденсатора. Проводники называются обкладкамиконденсатора.

Электроёмкость конденсатора определяется по формуле C ^q.

U
Конденсатор условно обозначается .

Соединение конденсаторов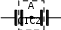

Рассмотрим последовательное соединение двух конденсаторов С₁ и С₂. Точка А между конденсаторами отделена от остальной цепи, поэтому её электрический заряд изменится не может. Так как до включения в цепь на-

чальный заряд точки был равен нулю, то q_A q_A1  q_A2  0 . Следовательно, заряды пластин кон-

денсаторов, примыкающих к точке А, равны между собой по величине, но противоположны по знаку. Но так как величина заряда пластин равна заряду конденсаторов, то заряды конденсато- ров в этом случае равные: q₁  q₂ .

Суммарный заряд точки А равен нулю, поэтому если отбросить эту точку вместе с прилегающими обкладками, то в схеме ничего не изменится. Т.к. заряды крайних пластин тоже одинаковы по величине, но разные по знаку, то получившийся конденсатор будет иметь такой же по величине заряд.

ИТОГ. Заряды последовательно соединенных конденсаторов одинаковы по величине. Общий заряд последовательно соединенных конденсаторов равен заряду каждого из конденса- торов. Для этого случая общее напряжение равно сумме напряжений на конденсаторах

U_ОБЩ =U₁+U₂. Заряды конденсаторов одинаковые q₁=q₂=q. Тогда

q ^CОБЩ

₌ q ₊ q C₁ C₂

. Поэтому

1

^CОБЩ

₌ 1 ₊ 1

C₁ C₂
. Припоследовательномсоединенииемкостискладываютсяпозаконуобрат-

ныхвеличин.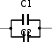
Расчет емкости при параллельном соединении конденсаторов. Для этого случая напряжения на конденсаторах одинаковые U₁=U₂=U. Суммарный заряд равен сумме зарядов q_ОБЩ=q₁+q₂ или С_ОБЩU=C₁U+C₂U

Тогда С_ОБЩ =C₁+C₂ . При параллельном соединении конденсаторов емкостисуммируются.

1 q CU² q²

k
Энергия заряженного конденсатора W _{ 2} _kq_k ₂ U

 .

2 2C

Замечание. Суммарный заряд обкладок конденсатора равен нулю. Конденсатор накапливает электрическую энергию путём разделения электрических зарядов.

Примеры по расчёту ёмкости конденсаторов.

Плоский(воздушный)конденсатор представляет собой две параллельные пластины, расстояние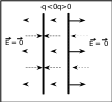

между которыми много меньше размеров пластин, так что поле между пластинами можно считать однородным. Пусть между пластинами находится вакуум (воздух), поэтому =1.

В этом случае при расчете картины поля можно пользо- ваться результатами, полученными для поля бесконечной заря- женной пластины. Так как заряды и площади пластин равны по величине, то и величина напряженности поля, создаваемого каж-

дой из пластин одинакова E =

q 2ε₀S
, но направления векторов напряженности разные (вектор

напряженности от отрицательно заряженной пластины показан пунктиром). Между пластинами векторы напряженности направлены одинаково, поэтому величина суммарной напряженности равна сумме величин напряженностей

^EВНУТРИ

 E_

• 
  E_-
  

_ q

2 S

• 
  q
  

2 S

 ^q.

 S

0 0 0
Снаружи пластин векторы напряженности поля направлены противоположно, поэтому напря- женность поля снаружи равна нулю. Таким образом, у конденсатора напряженность поля от- лична от нуля только между пластинами.

Так как электростатическое поле является полем консервативной силы, то интеграл

→ ^→

₁  ₂  _{ }E,dl_



не зависит от траектории, поэтому разность потенциалов между пластинами

можно найти, например, вдоль перпендикуляра, соединяющего пластины, длина которого равна

d: U  -  E

 d ^{q d}, где d – расстояние между пластинами. Тогда электроёмкость

1 2 ВНУТРИ

₀ S

плоского (воздушного) конденсатора C ^q

_ ₀ S_.

U d

Цилиндрический (воздушный) конденсатор представляет собой два коаксиальных цилиндра одинаковой длины, вложенных друг в друга так, что расстояние между обкладками много меньше размеров обкладок.

Пусть длина конденсатора L, заряд внутренней обкладки по- ложительный q>0. Радиусы обкладок R₁ и R₂, R₁< R₂. Величина на- пряжённости поля между обкладками на расстоянии rот внутренней

обкладки R₁<r< R₂:

E ^q

2₀ Lr

. Напряжение между обкладками

^R2 → <sup>→

R2</sup> qdr q

^ R^

U ₁  ₂ 

_{ }E,dl_  _

 ln_² _ .

R₁ R₁

2₀ Lr

2₀ L

 ^R1 

Поэтому электроёмкость цилиндрического (воздушного) конденсато-

ра C ^q

U

_ 2₀ L<sub>.

ln</sub>^ R₂ ^

 _R

 1 

Сферический (воздушный) конденсатор представляет собой две вложенные концентрические сферы с радиусами обкладок R₁ и R₂, R₁< R₂. Пусть заряд внутренней обкладки положительный

q>0. Величина напряжённости поля между обкладками на расстоя-

q

нии rот внутренней обкладки R₁<r< R₂:
между обкладками

E . Напряжение


0
4 r²

^R2 → <sup>→

R2</sup> q q

^ 1 1 ^

U ₁  ₂ 

_{ }E,dl_  _{ 4 r2} dr _4

 _R^ _R

R₁ R₁

0 0 

1 2 

C ^q


4_{0 .}

Поэтому электроёмкость сферического (воздушного) конденсатора

^{U }1 _1 ^

 _{R R}

 1 2 
Объёмнаяплотностьэнергииэлектростатическогополя.

Рассмотрим плоский воздушный конденсатор. Энергия заряженного конденсатора

^{CU2  S} 2 ^{ E2}

^{W 0}  ^{E d}

2 2d

⁰S d.

2

Объём пространства между пластинами конденсатора V S d . Так поле между пластинами

W  E²

рассматриваем как однородное, то единица объема этого поля обладает энергией w ⁰.

Эта величина
w ^W

V

V 2

называется объёмнойплотностьюэнергии.

В случае, когда поле не является однородным объёмная плотность энергии определяется

соотношением

w ^dW.

dV

_E,D_

→ →
В веществе объёмная плотность энергии электрического поля определяется w .

2

В случае однородного изотропного диэлектрика

ε E² D²

D ₀ E, поэтому w⁰ .

→ → → → → →

2 2ε₀

→ →

_E,D_ _{0 }E,E_{ }E,P_

_{0 }E,E_

→ →
Т.к. D  ₀E P, то w ₂ 

_E,P_

• 
  , где
  

2 2

- энергия электрического поля

2

в вакууме;

- энергия поляризации вещества.

2

Пример. Рассмотрим заряженную тонкостенную сферу радиуса R. Одноименные заряды на сфере отталкиваются друг от друга. Эти силы отталкивания стремятся растянуть поверхность сферы. Можно считать, что изнутри сферы на стенки действует дополнительное давление, рас- пирающее сферу и вызванное наличием электрического заряда на поверхности.

Напряженность поля внутри сферы равна нулю, поэтому объемная плотность энергии электрического поля wотлична от нуля только снаружи сферы.

При небольшом увеличении радиуса на dR сферы её объём увеличится, при этом в той части окружающего пространства, которая попала внутрь сферы, объёмная плотность энергии станет равной нулю. Следовательно, изменение энергии поля снаружи будет равно

dW wdV wSdR(S– площадь поверхности). Но, при расширении сферы, силы давления

внутри сферы совершат работу A pSdR. Так как A dW, то pSdR wSdR, откуда

p w.

Пример. Найдем силы, действующие на пластины в заряженном плоском конденсаторе, отклю- чённом от источника. Пластины заряжены разноименно, поэтому они притягиваются. Предпо- ложим, что пластины сблизились на малую величину x. Тогда объём конденсатора уменьшился на величину dV=xS, поэтому энергия конденсатора уменьшилась на dW=wdV. Силы притяже- ния совершат работу A=Fx. Так как A= dW, то Fx=wxS.Поэтому величина силы равна F=wS.

Дополнительное давление, которое создают эти силы, равно

p ^F w.

S

Приведённые примеры показывают, что на тела, находящиеся в электрическом поле, действуют силы, вызывающие дополнительное давление, равное объёмной плотности энергии. Давление,вызванноеналичиемэлектрическогополяравнообъёмнойплотностиэнергии.

Замечание. Силы, действующие на тела со стороны какого-то поля, называются пондемотор-ными.