Криптография. 09 генераторы. Лекция Криптографические генераторы
 Скачать 120.24 Kb. Скачать 120.24 Kb.
|
|
Лекция 9. Криптографические генераторы Криптографические генераторы обычно реализуются программно и используются для выработки псевдослучайных последовательностей 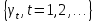 над конечным полем над конечным полем 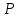 . Из этих последовательностей, называемых гаммой получаются ключи криптосистем, случайные инициальные векторы, управляющая гамма поточных шифров. . Из этих последовательностей, называемых гаммой получаются ключи криптосистем, случайные инициальные векторы, управляющая гамма поточных шифров. Обозначим в гамме 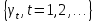 : :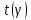 — длина периода, — длина периода, 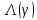 — линейная сложность. — линейная сложность.Базовым элементом криптосхем многих генераторов является ЛРС с максимальной длиной периода, выходная гамма которого (ЛРП) имеет и хорошие статистические свойства. В то же время линейная сложность ЛРП равна ее порядку, что позволяет восстанавливать всю ЛРП по ее сравнительно небольшому отрезку. Эта слабость ЛРС позволяет ее использовать только в сочетании с различными функциональными узлами и элементами памяти. Назначение последних — привнести в функции криптосистемы нелинейные свойства и зависимость каждого знака выхода от возможно большего числа знаков входа, не теряя положительные свойства ЛРП. Гамма такого генератора есть определенное усложнение ЛРП. Рассмотрим классы генераторов, построенных на основе ЛРС. 9.1. Фильтрующие генераторы. Фильтрующий генератор (ф.г.) над полем 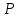 генерирует гамму по формуле генерирует гамму по формуле  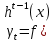 , ,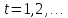 , (9.1) , (9.1)где 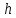 - линейная подстановка пространства - линейная подстановка пространства  , выполняемая ЛРС длины , выполняемая ЛРС длины 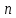 , ,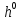 – тождественная подстановка; – тождественная подстановка; 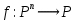 — функция, называемая фильтром или фильтрующей функцией; — функция, называемая фильтром или фильтрующей функцией; 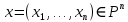 – ненулевое начальное состояние ЛРС. Ф.г. называется нелинейным, если фильтрнелинейный. Ключевые элементы ф.г. — начальное состояние ЛРС, ключами может быть также характеристический многочлен ЛРС и фильтр – ненулевое начальное состояние ЛРС. Ф.г. называется нелинейным, если фильтрнелинейный. Ключевые элементы ф.г. — начальное состояние ЛРС, ключами может быть также характеристический многочлен ЛРС и фильтр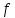 . Схема ф.г. дана на рис. 9.1. . Схема ф.г. дана на рис. 9.1.Пусть 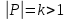 , , 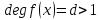 . Отметим свойства ф.г.: . Отметим свойства ф.г.: 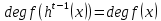 , , 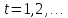 ; ;если ф.г. использует ЛРС  и сбалансированный фильтр, то и сбалансированный фильтр, то 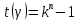 , и частоты «1» и «0» на периоде гаммы различаются на 1; , и частоты «1» и «0» на периоде гаммы различаются на 1;нелинейные свойства гаммы обеспечены нелинейным фильтром:  , ,где 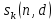 —число различных конъюнкций от —число различных конъюнкций от  ранга от 0 до ранга от 0 до 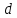 . В случае . В случае 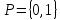 верна оценка верна оценка 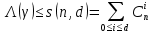 . .Получение оценки снизу для () требует учета более глубоких свойств фильтра. Гамма ф.г. имеет высокую линейную сложность при фильтре высокой степени нелинейности. При простом 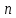 доля ф.г. на базе ЛРС доля ф.г. на базе ЛРС , у которых линейная сложность достигает наибольшего значения , у которых линейная сложность достигает наибольшего значения 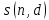 , стремится к 1 [26]. , стремится к 1 [26].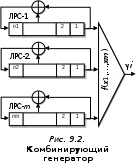 9.2. Комбинирующие генераторы (комб.г.) являются усложнением фильтрующих генераторов. Они построены на основе ЛРС-1 длины 9.2. Комбинирующие генераторы (комб.г.) являются усложнением фильтрующих генераторов. Они построены на основе ЛРС-1 длины 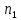 , …, ЛРС- , …, ЛРС-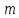 длины длины 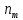 над над 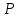 , , 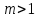 , и комбинирующей функции , и комбинирующей функции 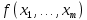 , на вход которой поступают знаки ЛРП-1, …, ЛРП- , на вход которой поступают знаки ЛРП-1, …, ЛРП-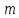 . Комб.г. изображен на рис. 9.2. . Комб.г. изображен на рис. 9.2.Обозначим  +…+ +…+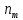 , и положим, не теряя общности: , и положим, не теряя общности: 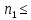 … …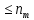 . Уравнения гаммообразования комб.г. имеют вид: . Уравнения гаммообразования комб.г. имеют вид: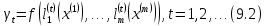 где 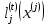 есть есть 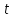 -й знак, генерируемый ЛРП- -й знак, генерируемый ЛРП-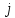 при начальном состоянии при начальном состоянии 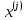 , , 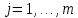 . . Комбинирующий генератор называется нелинейным, если нелинейна комбинирующая функция. Ключевые элементы комб.г. — начальные состояния всех ЛРС, ключами могут быть также их характеристические многочлены и комбинирующая функция. Начальные состояния всех ЛРС образуют начальное состояние генератора. Начальное состояние комб.г. назовем неособенным, если начальное состояние каждого ЛРС ненулевое. Наилучшие криптографические свойства комб.г. имеет в том случае, когда комбинирующая функция зависит существенно от 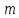 переменных и начальное состояние неособенное, иначе данный комб.г. вырождается в комб.г. с меньшим числом ЛРС. Далее считаем, что эти условия выполнены. переменных и начальное состояние неособенное, иначе данный комб.г. вырождается в комб.г. с меньшим числом ЛРС. Далее считаем, что эти условия выполнены.Отметим, что 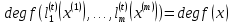 , , 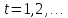 . .Оценим линейную сложность гаммы генератора. Каждому каноническому полиному 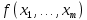 над над 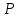 соответствует полином соответствует полином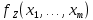 над кольцом над кольцом 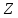 целых чисел, полученный из целых чисел, полученный из 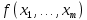 заменой всех ненулевых коэффициентов на 1и заменой сложения и умножения в поле Р сложением и умножением в Z. заменой всех ненулевых коэффициентов на 1и заменой сложения и умножения в поле Р сложением и умножением в Z.Теорема 9.1. При любом неособенном начальном состоянии комб.г. 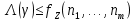 . .Данная оценка в некоторых условиях вырождается в точное равенство, в частности, еслиполе 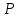 простое, и характеристические многочлены всех ЛРС примитивные, имеющие попарно взаимно простые степени [1, 26]. простое, и характеристические многочлены всех ЛРС примитивные, имеющие попарно взаимно простые степени [1, 26].При определенных ЛРС и функции 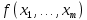 гамма комб.г. имеет хорошие статистические свойства и большую длину периода. В частности, если ЛРС-1, …, ЛРС- гамма комб.г. имеет хорошие статистические свойства и большую длину периода. В частности, если ЛРС-1, …, ЛРС-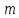 генерируют гаммы с попарно взаимно простыми длинами периодов генерируют гаммы с попарно взаимно простыми длинами периодов 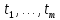 и функция и функция 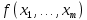 биективна по каждой переменной, то биективна по каждой переменной, то 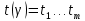 . Если каждая ЛРС имеет максимальную длину периода, то . Если каждая ЛРС имеет максимальную длину периода, то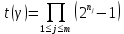 . .Теорема 9.2. Если функция 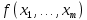 равновероятна, то равновероятна, то 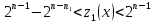 , ,где 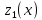 число единиц на периоде гаммы комб.г. при начальном состоянии число единиц на периоде гаммы комб.г. при начальном состоянии 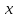 . .9.3. Аддитивные генераторы (АГ). АГ предназначены для генерации векторов или 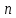 -битовых чисел (элементов кольца вычетов -битовых чисел (элементов кольца вычетов 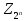 ). Они синтезируют идеи построения ЛРС и ЛКГ. Пусть ). Они синтезируют идеи построения ЛРС и ЛКГ. Пусть 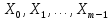 суть числа, образующие начальное состояние генератора, тогда суть числа, образующие начальное состояние генератора, тогда 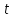 -й знак гаммы -й знак гаммы 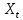 определен законом рекурсии, определен законом рекурсии, 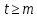 , ,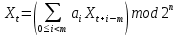 , ,где коэффициенты 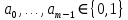 и выбраны так, чтобы при замене сложения по модулю и выбраны так, чтобы при замене сложения по модулю 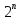 операцией операцией 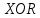 -суммирования закону рекурсии соответствовал примитивный характеристический многочлен. Для подпоследовательности младших разрядов и, следовательно, для всей гаммы -суммирования закону рекурсии соответствовал примитивный характеристический многочлен. Для подпоследовательности младших разрядов и, следовательно, для всей гаммы 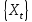 это гарантирует длинупериода не меньше это гарантирует длинупериода не меньше 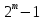 . .АГ нестойки, но используются как базовые блоки для построения более стойких генераторов (Fish — Fibonacci Shrinking Generator, Pike, Mush). Свойства АГ улучшаются при модификации обратной связи. 9.4. Корреляционные атаки. Корреляционные атаки часто применяют для анализа генераторов гаммы в СПШ, построенных как композиция нескольких функциональных блоков и узлов типа ЛРС. Ключом генератора являются начальные состояния элементов памяти, ключами могут быть также параметры функциональных блоков. Идея корреляционных атак заключается в использовании ненулевой взаимной корреляции (если таковая имеется) между выходной гаммой генератора и промежуточной гаммой некоторого функционального блока или узла. Например, в ф.г. и комб.г. может быть взаимная корреляция между выходной гаммой и гаммой некоторых ЛРС [18, 19]. При наличии корреляции можно поэтапно определить по выходной гамме начальные состояния ряда ЛРС. Опробуя состояния регистра, отбраковываем как ложные (с помощью различения статистических гипотез) те из них, при которых гамма регистра не коррелирует с выходной гаммой. Проиллюстрируем технику на примере комб.г. Геффе, на основе генерирующих регистров ЛРС-1, ЛРС-2 и управляющего регистра ЛРС-3 длин 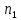 , , 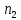 и и 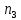 соответственно. Комб. функция соответственно. Комб. функция 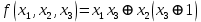 , она совпадает с функцией x1 (а также с функцией x2) с вероятностью 3/4 при случайном равновероятном выборе набора , она совпадает с функцией x1 (а также с функцией x2) с вероятностью 3/4 при случайном равновероятном выборе набора 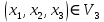 . Значит, гамма генератора совпадает с выходом ЛРС-1 примерно для 75% знаков. Опробуем начальные состояния ЛРС-1 и отбракуем «ложные» значения статистическим методом, генерируя знаки выхода ЛРС-1 и наблюдая частоту их совпадения с соответствующими знаками гаммы генератора. При истинном начальном состоянии частота совпадения знаков в последовательностях длины . Значит, гамма генератора совпадает с выходом ЛРС-1 примерно для 75% знаков. Опробуем начальные состояния ЛРС-1 и отбракуем «ложные» значения статистическим методом, генерируя знаки выхода ЛРС-1 и наблюдая частоту их совпадения с соответствующими знаками гаммы генератора. При истинном начальном состоянии частота совпадения знаков в последовательностях длины 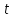 распределена по нормальному закону с математическим ожиданием распределена по нормальному закону с математическим ожиданием 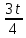 и с дисперсией и с дисперсией  . При ложных значениях имеем нормальное распределение с математическим ожиданием . При ложных значениях имеем нормальное распределение с математическим ожиданием 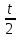 и с дисперсией и с дисперсией 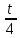 t. Для отбраковки ложного значения достаточно примерно 16 сравнений знаков. Значит, начальное состояние одного из генерирующих ЛРС определяется в среднем после t. Для отбраковки ложного значения достаточно примерно 16 сравнений знаков. Значит, начальное состояние одного из генерирующих ЛРС определяется в среднем после  сравнений, где сравнений, где 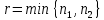 . .Трудоемкость вскрытия других элементов ключа менее значительна. Наилучшее противодействие корреляционным атакам достигается при комбинирующих функциях, имеющих высокий корреляционный иммунитет. Вместе с тем, известно [28], что корреляционный иммунитет комбинирующей функции связан с линейной сложностью гаммы генератора, ослабление одной характеристики влечет усиление другой. Пример 9.1. Генератор Геффе использует комбинацию генерирующих ЛРС-1, ЛРС-2 и управляющего ЛРС-3. Комбинирующая функция 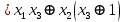 . В каждом такте знак гаммы при управляющем знаке 1 совпадает с выходным знаком ЛРС-1, а при управляющем знаке 0 — с выходным знаком ЛРС-2. Если все ЛРС имеют максимальные периоды и их длины . В каждом такте знак гаммы при управляющем знаке 1 совпадает с выходным знаком ЛРС-1, а при управляющем знаке 0 — с выходным знаком ЛРС-2. Если все ЛРС имеют максимальные периоды и их длины 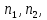 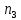 попарно взаимно просты, то период гаммы равен произведению периодов ЛРС, а линейная сложность гаммы генератора равна попарно взаимно просты, то период гаммы равен произведению периодов ЛРС, а линейная сложность гаммы генератора равна 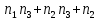 . .Пример 9.2 Пороговый генератор использует комбинацию нечетного числа 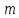 регистров. Комбинирующая функция регистров. Комбинирующая функция 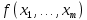 , называемая функцией мажорирования, равна 1 , называемая функцией мажорирования, равна 1  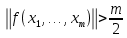 . При подходящих ЛРС линейная сложность длина периода гаммы порогового генератора равна произведению периодов ЛРС. При . При подходящих ЛРС линейная сложность длина периода гаммы порогового генератора равна произведению периодов ЛРС. При 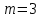 и и 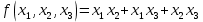 линейная сложность гаммы равна линейная сложность гаммы равна 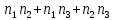 . .Наилучшие криптографические свойства фильтрующих и комбинирующих генераторов достигаются при использовании функций высокой степени нелинейности, техническая и программная реализация которых весьма сложна. Трудность достижения приемлемого компромисса стимулировала поиск новых конструкций генераторов гаммы. 9.5. Генераторы гаммы с неравномерным движением. Информация в элементах памяти рассмотренных схем обновляется при любом состоянии памяти равномерно (в каждом такте функционирования). Вместе с тем, гамма усложняется, если продвижение информации в регистрах зависит от последовательности, вырабатываемой другим регистром, т.е. является неравномерным. Построенные по такому принципу генераторы гаммы называются генераторами гаммы с неравномерным движением. Зависимость закона движения информации проявляется, например, в усечении (удалении), реже — в дублировании некоторых битов исходной гаммы. Эффект неравномерного движения достигается с помощью внешнего управления регистрами генератора гаммы или с помощью самоуправления. Один из способов внешнего управления состоит в последовательном соединении 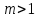 функциональных узлов, где предыдущий узел управляет движением информации в следующем, последний узел называют генерирующим. Если функциональных узлов, где предыдущий узел управляет движением информации в следующем, последний узел называют генерирующим. Если 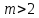 , то такое соединение называют каскадным с числом каскадов , то такое соединение называют каскадным с числом каскадов 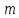 . Конструкция каскада может быть простой, например, каскад — это ЛРС, и управление реализуется в каждый такт в виде зависимости от управляющего знака величины «продвижения» информации генерирующего автомата. . Конструкция каскада может быть простой, например, каскад — это ЛРС, и управление реализуется в каждый такт в виде зависимости от управляющего знака величины «продвижения» информации генерирующего автомата.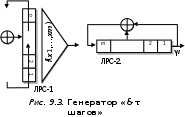 Другой способ основан на нескольких взаимно управляемых автоматах, совместно генерирующих гамму (см. генератор шифра А5 [13]). При самоуправлении величина «продвижения» информации в регистрах автомата управляется гаммой, зависящей от состояния всех регистров памяти. Другой способ основан на нескольких взаимно управляемых автоматах, совместно генерирующих гамму (см. генератор шифра А5 [13]). При самоуправлении величина «продвижения» информации в регистрах автомата управляется гаммой, зависящей от состояния всех регистров памяти.9.5.1. Схемы с внешним управлением. Для двоичного ЛРС- 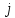 , , 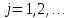 , обозначим: , обозначим: 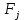 — характеристический многочлен; — характеристический многочлен; 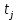 — длина периода выходной гаммы ( — длина периода выходной гаммы (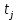 не зависит от начального состояния при ЛРС с максимальной длиной периода). не зависит от начального состояния при ЛРС с максимальной длиной периода).Генератор « 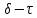 шагов» - двухкаскадная схема (рис. 9.3), где шагов» - двухкаскадная схема (рис. 9.3), где 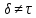 (при ( (при (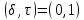 — генератор «стоп-вперед»), управляющий автомат есть ф.г. на базе ЛРС-1 длины — генератор «стоп-вперед»), управляющий автомат есть ф.г. на базе ЛРС-1 длины 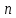 с фильтрующей булевой функцией с фильтрующей булевой функцией 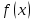 , генерирующий автомат есть ЛРС-2 длины , генерирующий автомат есть ЛРС-2 длины 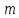 (гамма есть последовательность состояний его (гамма есть последовательность состояний его 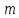 -й ячейки). Далее считаем, что -й ячейки). Далее считаем, что  , , 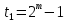 , ,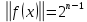 . . Обозначим: 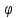 и и  — линейные подстановки, реализуемые соответственно ЛРС-1 на — линейные подстановки, реализуемые соответственно ЛРС-1 на 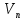 и ЛРС-2 на и ЛРС-2 на 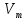 ; ; 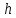 — нелинейная подстановка множества — нелинейная подстановка множества 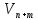 состояний генератора; состояний генератора; 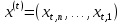 и и 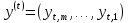 — состояния ЛРС-1 и ЛРС-2 в — состояния ЛРС-1 и ЛРС-2 в 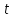 -м такте, -м такте, 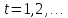 ; при ; при 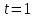 — начальные состояния. При любом состоянии — начальные состояния. При любом состоянии 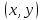 генератора подстановка генератора подстановка 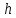 имеет вид: имеет вид: , ,где 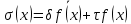 . Уравнения гаммообразования имеют вид . Уравнения гаммообразования имеют вид  , ,где 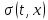 — величина «продвижения» ЛРС-2 после первых — величина «продвижения» ЛРС-2 после первых 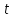 тактов: тактов: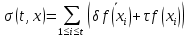 . .Лемма 9.1. Величина 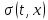 не зависит от не зависит от  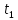 делит i. делит i.Доказательство. Обозначим: 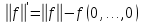 . .По условию  и на периоде ЛРС-1 имеется и на периоде ЛРС-1 имеется 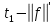 нулей и нулей и 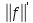 единиц. Тогда при единиц. Тогда при 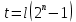 , ,  величина величина 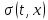 не зависит от не зависит от 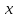 : : 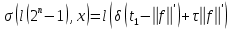 . .При 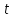 , не кратном , не кратном 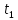 , независимость величины , независимость величины 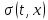 от от 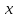 равносильна тому, что любой отрезок длины равносильна тому, что любой отрезок длины 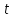 управляющей гаммы содержит одинаковое число единиц, тогда в управляющей гамме есть совпадения на расстоянии управляющей гаммы содержит одинаковое число единиц, тогда в управляющей гамме есть совпадения на расстоянии 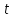 , значит, , значит, 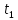 делит делит 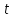 , что противоречит не кратности , что противоречит не кратности 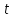 числу числу 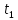 . . В соответствии с леммой 9.1 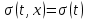 при при 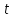 , кратных , кратных 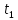 . Обозначим . Обозначим 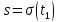 .Тогда оба регистра вернутся в начальное состояние при «продвижении» ЛРС-2 на .Тогда оба регистра вернутся в начальное состояние при «продвижении» ЛРС-2 на  шагов, достигаемом после шагов, достигаемом после 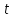 тактов, где тактов, где 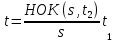 . Следовательно, длина периода . Следовательно, длина периода 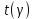 гаммы генератора достигает наибольшего значения гаммы генератора достигает наибольшего значения 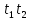 при при  . .Группа генератора « 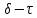 шагов» есть циклическая группа шагов» есть циклическая группа  . При начальном состоянии . При начальном состоянии 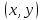 генераторасостояние после генераторасостояние после 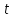 тактов есть тактов есть 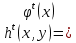 , ,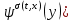 , , 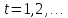 Отсюда подстановка Отсюда подстановка 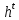 линейная линейная  величина величина 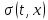 не зависит от не зависит от 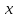 . Тем самым доказана следующая теорема. . Тем самым доказана следующая теорема. Теорема 9.3 [13]. Если управляющий блок генератора « 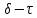 шагов» состоит из ф.г. на базе ЛРС шагов» состоит из ф.г. на базе ЛРС , ограничение фильтра , ограничение фильтра 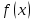 на на 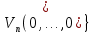 отлично от константы, а генерирующий блок есть ЛРС отлично от константы, а генерирующий блок есть ЛРС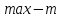 , то порядок линейной подгруппы группы , то порядок линейной подгруппы группы  равен равен 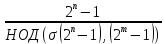 . .Для линейной сложности гаммы генератора верна оценка 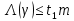 . . В генераторе «стоп-вперед» эта оценка достигается [17], если управляющий регистр есть ЛРС  и и  . Но статистические свойства его гаммы слабы: в среднем каждый 2-й бит выхода ЛРС-2 дублируется; из неравенства . Но статистические свойства его гаммы слабы: в среднем каждый 2-й бит выхода ЛРС-2 дублируется; из неравенства 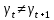 следует следует  , что упрощает нахождение состояний ЛРС-1 по гамме. , что упрощает нахождение состояний ЛРС-1 по гамме.Если 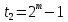 , то в гамме генератора «1-2 шага» при , то в гамме генератора «1-2 шага» при 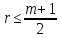 частота всех частота всех 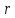 -грамм та же, что и в гамме ЛРС-2 при равномерном движении. -грамм та же, что и в гамме ЛРС-2 при равномерном движении. Генератор с перемежающимся шагом является усложнением генератора «стоп-вперед» с целью улучшения статистических свойств. Гамма образуется как сумма гамм двух генераторов «стоп-вперед» с генерирующими ЛРС-2 и ЛРС-3 длины 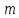 и и 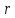 соответственно, имеющими общий управляющий блок — ф.г. с фильтром соответственно, имеющими общий управляющий блок — ф.г. с фильтром 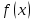 на базе ЛРС-1 длины на базе ЛРС-1 длины 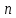 . Если в . Если в 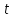 -м такте управляющий знак равен 1, то ЛРС-2 продвигается на 1 шаг, а ЛРС-3 простаивает; при управляющем знаке 0 — наоборот. Ключом генератора являются начальные состояния всех ЛРС. -м такте управляющий знак равен 1, то ЛРС-2 продвигается на 1 шаг, а ЛРС-3 простаивает; при управляющем знаке 0 — наоборот. Ключом генератора являются начальные состояния всех ЛРС. Длина периода |

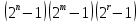 при попарно взаимно простых числах
при попарно взаимно простых числах 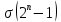 ,
, 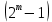 и
и 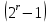 .
.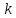 -грамм, где
-грамм, где 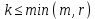 , близка к
, близка к 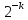 c отклонением порядка
c отклонением порядка 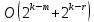 .
.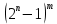 , а линейная сложность имеет порядок
, а линейная сложность имеет порядок 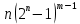 . При
. При 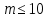 корреляция между гаммой ЛРС-1 и гаммой
корреляция между гаммой ЛРС-1 и гаммой 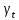 есть знак ЛРС-2 с номером такта, соответствующего
есть знак ЛРС-2 с номером такта, соответствующего 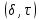 -самоусечения.
-самоусечения. 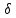 шагов, если знак управляющей гаммы (состояние
шагов, если знак управляющей гаммы (состояние 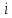 -й ячейки регистра) равен 1, и в противном случае информация в ЛРС продвигается на
-й ячейки регистра) равен 1, и в противном случае информация в ЛРС продвигается на 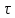 шагов, где
шагов, где 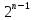 , доказательства не найдены.
, доказательства не найдены.