задачи на прогрессии. задачи на прогр. Решение. Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом и По формуле
 Скачать 198.59 Kb.
|
 1. На клетчатой бумаге с размером клетки  нарисована «змейка», представляющая собой ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 120.Решение. Длина змейки, изображенной на рисунке, составляет  и представляет арифметическую прогрессию, члены которой учтены два раза, первый член равен 10, а разность — 1.Найдем сумму арифметической прогрессии для змейки, звено последнее звено которой 120  Каждый член прогрессии должен быть учтен дважды, следовательно, длина змейки  Ответ: 14520. 2  . В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 16 квадратных столиков вдоль одной линии?Решение. Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом  и  По формуле n-го члена  найдем 16 член прогрессии, разность которой 2: Ответ: 34. 3. У Тани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 360 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 15см? Решение. Изменение высоты отскока мячика представляет собой геометрическую прогрессию с первым членом 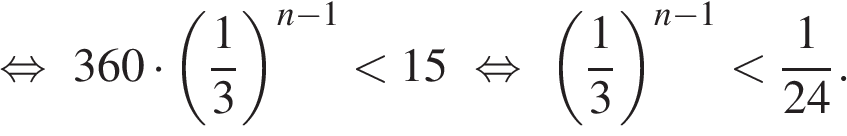 см и знаменателем  По формуле n-ого члена  найдем, после какого по счету отскока высота, на которую подлетит мячик, станет меньше 15 см.  Следовательно,  — минимальное целое значение, которое удовлетворяет неравенство, или счет отскока, после которого высота, на которую подлетит мячик, станет меньше 15 см.Ответ: 4. 1. Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 9 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд? Решение. Растущая скорость камня представляет собой арифметическую прогрессию с первым членом 9 и разностью 10. Найдем сумму этой прогрессии:  м.Ответ: 145. 2. В амфитеатре 14 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в восьмом ряду 36 мест. Сколько мест в последнем ряду амфитеатра? Решение. Число мест в ряду представляет собой арифметическую прогрессию с пятым членом  и восьмым  разность равна   По формуле n-го члена найдем 14 член прогрессии: Ответ: 54. 3. Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней. Решение. Пусть рабочие в первый день проложили  метров тоннеля, во второй —  , …, в последний —  метров тоннеля. Длина тоннеля  метров.   дней. Тогда в последний день рабочие проложили метров.Таким образом, рабочие в последний день проложили 97 метров тоннеля. Ответ: 97. 4. Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней. Решение. В первый день Вера подписала  открыток, во второй —  …, в последний —  открыток. Всего было подписано  открыток. Если количество подписываемых открыток увеличивалось на d каждый день, то  Тогда  Следовательно, за четвертый день было подписано 22 открытки. Ответ: 22. 5. Занятия йогой начинают с 15 минут в день и увеличивают на 10 минут время каждый следующий день. Сколько дней следует заниматься йогой в указанном режиме, чтобы суммарная продолжительность занятий составила 2 часа? Решение. Продолжительность занятий составляет арифметическую прогрессию с первым членом a1 = 15, разностью d = 10 и суммой прогрессии Sn = 120. Выразим количество дней n (n>0) из формулы суммы арифметической прогрессии:   Подставим значения в полученное выражение: 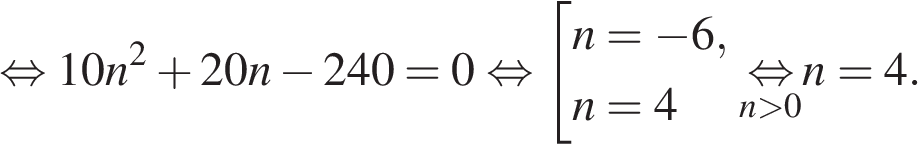  Ответ: 4 дня 3. Клиент взял в банке кредит в размере 50 000 р. на 5 лет под 20% годовых. Какую сумму он должен вернуть в банк в конце срока, если проценты начисляются ежегодно на текущую сумму долга и весь кредит с процентами возвращается в банк после срока? Решение. Пусть S0 = 50 000 руб., r = 0,2. Тогда сумма S (в рублях), которую необходимо вернуть, составляет  рублей.Ответ: 124 416. 11. В полночь в организме начало накапливаться ядовитое вещество, причем каждые три часа количество попадающего в организм вещества увеличивается вдвое. Сколько граммов вещества накопится в организме за сутки (начиная с нуля часов), если в период с 6 до 9 часов утра в организм попало 0,0008 г вещества? Решение. Количество попадающего в организм в течение каждого трехчасового промежутка вещества представляет собой геометрическую прогрессию со знаменателем 2. Общее количество попавшего в организм вещества является суммой геометрической прогрессии. Третий член геометрической прогрессии равен 0,0008, знаменатель равен 2. Поэтому первый член прогрессии равен 0,0002, а сумма первых 8 членов равна  Ответ: 0,051 12. Служившему воину дано вознаграждение: за первую рану 1 копейка, за другую — 2 копейки, за третью — 4 копейки и т. д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран. Решение. Количество ран составляет геометрическую прогрессию с первым членом  вторым членом  а значит, знаменатель геометрической прогрессии  Найдем сумму членов геометрической прогрессии: По условию, эта сумма равна 65 535. Чтобы узнать количество ран, необходимо найти количество членов прогрессии n:  Ответ: 16. 1.На клетчатой бумаге с размером клетки нарисована «змейка», представляющая собой ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 120.2. В амфитеатре 14 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в восьмом ряду 36 мест. Сколько мест в последнем ряду амфитеатра? 3. У Тани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 360 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 15см? 4. В полночь в организме начало накапливаться ядовитое вещество, причем каждые три часа количество попадающего в организм вещества увеличивается вдвое. Сколько граммов вещества накопится в организме за сутки (начиная с нуля часов), если в период с 6 до 9 часов утра в организм попало 0,0008 г вещества? 5. Занятия йогой начинают с 15 минут в день и увеличивают на 10 минут время каждый следующий день. Сколько дней следует заниматься йогой в указанном режиме, чтобы суммарная продолжительность занятий составила 2 часа? 1. Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 9 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд? 2. В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 16 квадратных столиков вдоль одной линии? 3. Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней. 4. Служившему воину дано вознаграждение: за первую рану 1 копейка, за другую — 2 копейки, за третью — 4 копейки и т. д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран. 5. Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней. |