Лекция Магнитное поле в вакууме
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Семестр 3. Лекция 5. Лекция 5. Магнитное поле в вакууме. Вектор индукции магнитного поля. Закон Био-Савара. Принцип суперпозиции магнитных полей. Поле прямого и кругового токов. Теорема о циркуляции вектора индукции магнитного поля в интегральной и дифференциальной формах. (Расчёт магнитного поля тороида и соленоида). Исследуя экспериментально силовое воздействие магнитного поля на проводник с током, А. Ампер установил, что сила Это соотношение получило название закона Ампера. Опыт показывает, что электрические токи взаимодействуют между собой. Закон Ампера позволяет рассчитать силу взаимодействия (на единицу длины) в вакууме двух прямолинейных тонких параллельных проводников с токами I1 и I2 , расстояние между которыми равно b: Одинаково направленные токи притягиваются, противоположно направленные – отталкиваются. Константа в вакууме имеет вид Замечание. Полезное соотношение: Замечание. Закон Ампера связывает механическое понятие силы с единицами измерения силы тока и электрического заряда. По современным представлениям токи взаимодействует между собой посредством промежуточной среды, которая называется магнитным полем. Магнитное поле характеризуется вектором магнитной индукции Магнитное поле проявляется в действии на движущиеся заряды (токи). На покоящиеся заряды магнитное поле не действует. Магнитное поле не имеет источников - оно создается только движущимися зарядами (электрическим током), поэтому силовые линии магнитного поля являются замкнутыми линиями. Принцип суперпозиции для магнитного поля: вектор индукции магнитного поля, создаваемого системой движущихся электрических зарядов (электрических токов), равен векторной сумме индукций магнитных полей, создаваемых каждым из движущихся электрических зарядов (токов) в отдельности: А 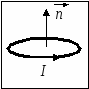 налогом пробного заряда для магнитного поля является пробный контур с током очень маленьких размеров. Этот контур является ориентированным – направление нормали к площадке, ограниченной контуром, согласовано с направлением тока в нём правилом буравчика (правого винта). Опыт показывает, что на пробный контур действует вращающий момент сил, зависящий от угла между вектором индукции магнитного поля и вектором нормали к площадке, ограниченной контуром, а также от силы тока и величины площадки. Максимальное значение момента даётся выражением налогом пробного заряда для магнитного поля является пробный контур с током очень маленьких размеров. Этот контур является ориентированным – направление нормали к площадке, ограниченной контуром, согласовано с направлением тока в нём правилом буравчика (правого винта). Опыт показывает, что на пробный контур действует вращающий момент сил, зависящий от угла между вектором индукции магнитного поля и вектором нормали к площадке, ограниченной контуром, а также от силы тока и величины площадки. Максимальное значение момента даётся выражением Определение. Магнитным моментом контура (с постоянным) током называется векторная величина где S- величина площадки, ограниченной контуром, I – сила тока. Единица измерения магнитного момента: Ам2 (Амперм2). Закон Био-Савара-Лапласа. Опыт показывает, что магнитная индукция 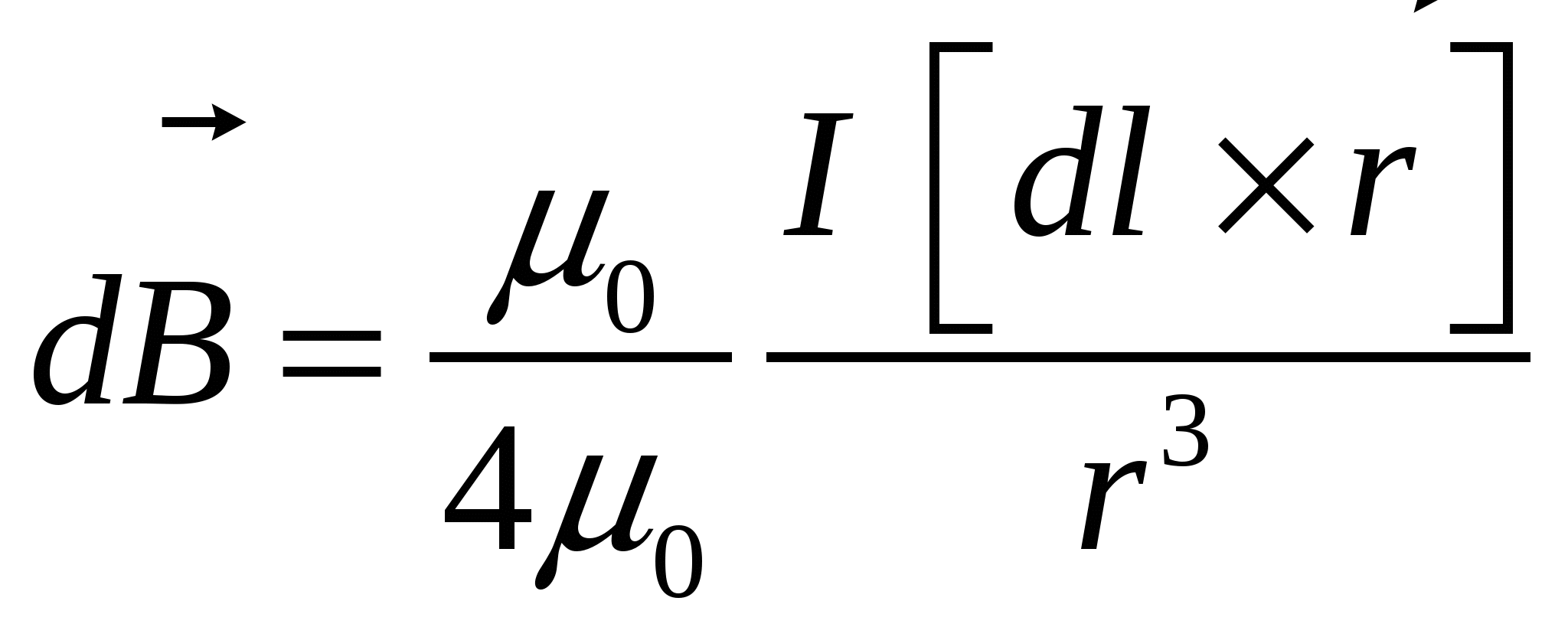 . .М 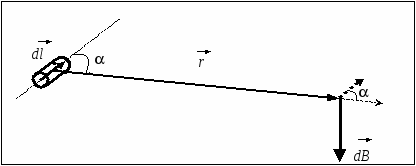 одуль индукции магнитного поля: 1) Рассмотрим магнитное поле, создаваемое длинным тонким прямым проводом, по которому течет постоянный ток силой I. Найдём величину и направление вектора магнитной индукции в точке, находящейся на расстоянии R от провода. Применим принцип суперпозиции где 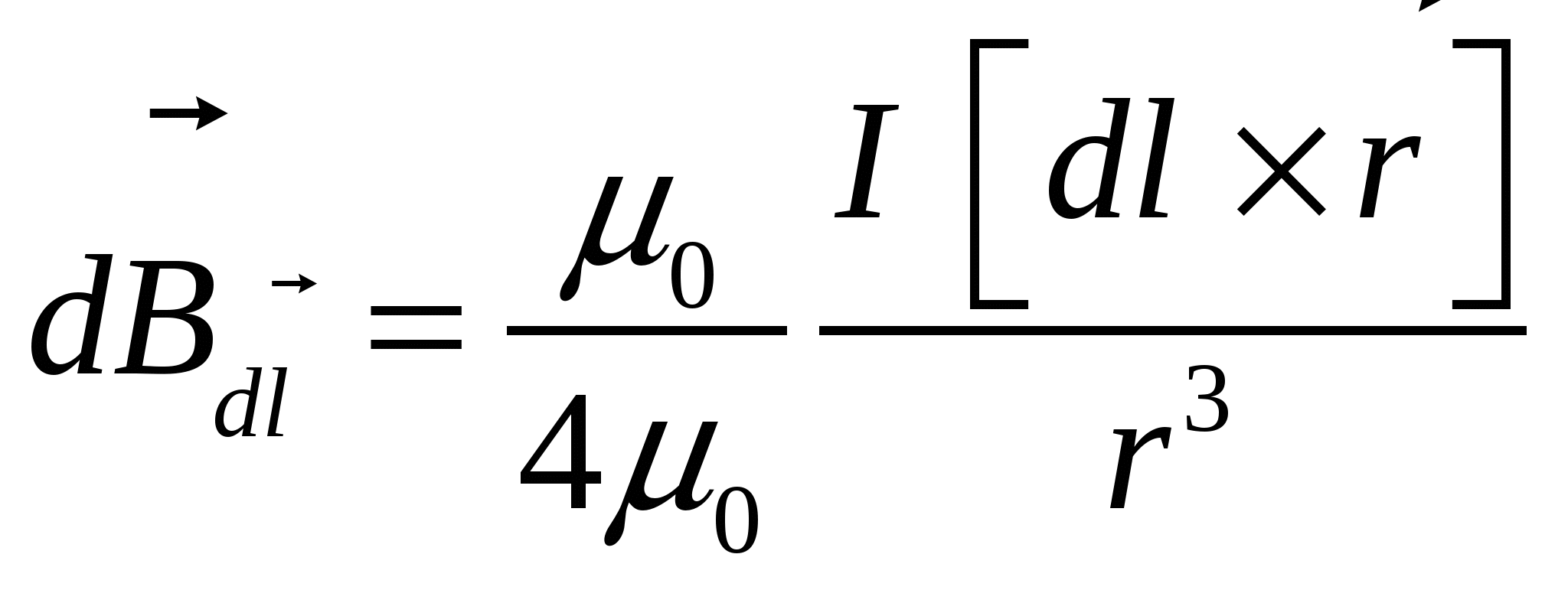 - вектор магнитной индукции, создаваемый элементом тока - вектор магнитной индукции, создаваемый элементом тока В 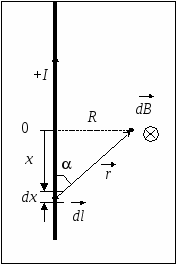 екторы екторы Введём координату х, отсчитываемую от точки пересечения провода и перпендикуляра к проводу, восстановленного из точки наблюдения. Тогда 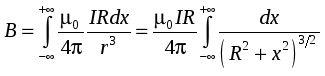 . .Но 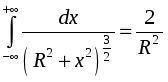 (см. лекцию № 1). (см. лекцию № 1).Окончательно, величина индукции магнитного поля на расстоянии R от тонкого длинного прямого провода с постоянным током I определяется соотношением: 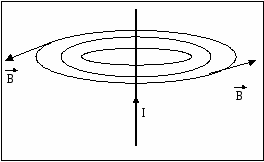 . .Силовые линии магнитного поля, создаваемого током в бесконечно длинном прямом проводнике, представляют собой окружности, лежащие в плоскости, перпендикулярной проводу, и с центром на оси провода. Направление вектора 2) Рассмотрим магнитное поле, создаваемое круговым контуром с постоянным током, на оси контура. 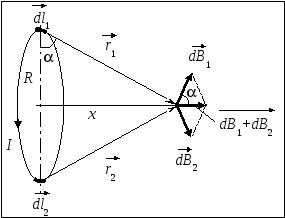 По контуру течёт ток силой I, радиус контура R. Найдём величину индукции магнитного поля в точке, находящейся на расстоянии x от плоскости контура вдоль его оси. По контуру течёт ток силой I, радиус контура R. Найдём величину индукции магнитного поля в точке, находящейся на расстоянии x от плоскости контура вдоль его оси.Любые два элемента Т.к. образующая конуса перпендикулярна касательной к основанию, то угол между векторами Для всех элементов 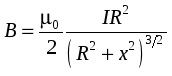 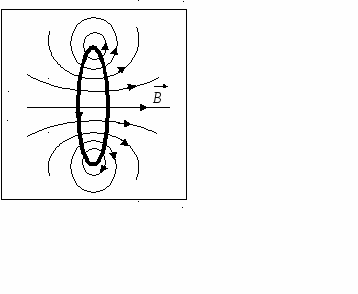 . .С учётом определения магнитного момента контура 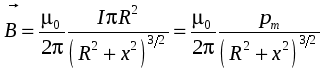 . .Замечание. Картина силовых линий магнитного поля кольца обладает осевой симметрией, поэтому вектор индукции в каждой точке плоскости кольца направлен перпендикулярно этой плоскости. Кроме того, в каждой точке поля вектор Теорема о циркуляции вектора магнитной индукции. Так как силовые линии магнитного поля замкнутые, то это поле является вихревым, т.е. П 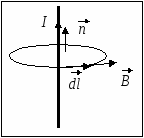 ример. Найдем циркуляцию вектора магнитной индукции поля, создаваемого прямым проводом с током. В качестве контура Г возьмём какую-нибудь силовую линию (представляющую собой, как нам уже известно, окружность с центром на оси провода и лежащую в плоскости, перпендикулярной к проводу). Пусть радиус этой линии равен R, тогда величина магнитной индукции на этой линии постоянна и равна ример. Найдем циркуляцию вектора магнитной индукции поля, создаваемого прямым проводом с током. В качестве контура Г возьмём какую-нибудь силовую линию (представляющую собой, как нам уже известно, окружность с центром на оси провода и лежащую в плоскости, перпендикулярной к проводу). Пусть радиус этой линии равен R, тогда величина магнитной индукции на этой линии постоянна и равна Выберем ориентацию на силовой линии так, чтобы векторы Этот результат не является случайным, его можно обобщить в виде теоремы о циркуляции вектора индукции магнитного поля циркуляция вектора индукции магнитного поля по любому ориентированному замкнутому контуру пропорциональна алгебраической сумме токов, пронизывающих ориентированную площадку, ограниченную контуром. Ориентация контура и площадки согласованы правилом правого винта. Коэффициент пропорциональности – магнитная постоянная: Сила тока берётся со знаком плюс, если угол между направлением тока и направлением нормали к площадке меньше 90 градусов, и минус - если больше. Если ввести векторное поле плотности тока получаем дифференциальную форму записи теоремы о циркуляции вектора магнитной индукции: Замечание. Хоть магнитное поле и является вихревым, но отсюда не следует, что циркуляция вектора магнитной индукции всегда отлична от нуля. Например, если контур Г охватывает два одинаковых по силе тока, но пронизывающих площадку в разных направлениях, то для них Идеальным соленоидом называется бесконечный тонкий проводник, намотанный на поверхность бесконечного кругового цилиндра так, что при этом круговые витки проводника перпендикулярны оси цилиндра. Замечание. В таком соленоиде нет составляющей электрического тока, направленной вдоль оси цилиндра, а только круговые токи в каждом из поперечных сечений. Поэтому можно считать, что соленоид составлен из бесконечного числа одинаковых витков, по которым течёт одинаковый по направлению и силе ток. Плотностью намотки соленоида n называется величина равная отношению количества витков N на некотором участке соленоида к длине этого участка l: 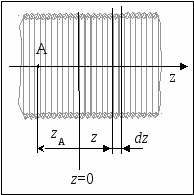 Найдем величину индукции магнитного поля в какой-нибудь точке А на оси соленоида. Пусть сила тока в соленоиде равна I. Радиус витков R. Плотность намотки n. Найдем величину индукции магнитного поля в какой-нибудь точке А на оси соленоида. Пусть сила тока в соленоиде равна I. Радиус витков R. Плотность намотки n. Для нахождения индукции магнитного поля в этой точке, применим принцип суперпозиции для магнитного поля – вектор индукции Введём вдоль оси соленоида ось z. Выделим в соленоиде какое-либо сечение, координату которого примем за ноль (z=0). Пусть точка А имеет координату zА. Небольшая часть соленоида, длина которой равна dz и которая находится в сечении с координатой z, содержит количество витков 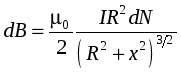 , где расстояние от точки А до этого сечения равно , где расстояние от точки А до этого сечения равно Тогда 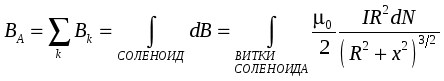 или или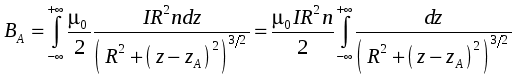 . .Делаем замену переменных: 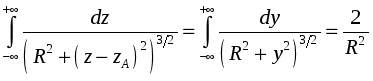 . .Поэтому величина магнитной индукции на оси соленоида равна: Обсудим расположение силовых линий магнитного поля соленоида (и внутри, и снаружи). Так как магнитное поле соленоида создаётся кольцами с током, то вектор индукции в каждой точке поля лежит в продольной плоскости соленоида (любой плоскости, проходящей через ось соленоида). 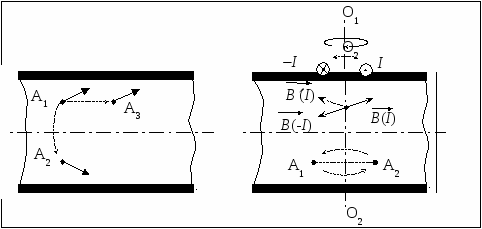 Докажем, что в произвольных точках A1, A2, A3, находящихся на равном расстоянии от оси, вектор индукции 1) Пусть точки A1 и A2 находятся в одном поперечном сечении. Так как магнитное поле соленоида обладает осевой симметрией, то поворотом вокруг оси можно перенести точку A1 в A2 (и наоборот). Векторы, находящиеся в этих точках должны перейти друг в друга (т.к. они принадлежат одному векторному полю). 2) Пусть точки A1 и A3 находятся в одном продольном сечении. Так как магнитное поле соленоида обладает симметрией сдвига вдоль оси, то сдвигом можно перенести точку A1 в A3 (и наоборот). Векторы, находящиеся в этих точках должны перейти друг в друга (т.к. они принадлежат одному векторному полю). Докажем теперь, что вектор индукции магнитного поля соленоида в каждой точке направлен параллельно оси соленоида. Для этого рассмотрим вектор Следовательно, силовые линии магнитного поля внутри и снаружи параллельны оси соленоида, а величина индукции зависит только от расстояния до оси соленоида. Рассмотрим циркуляцию индукции векторного поля по некоторому квадратному контуру Г1, который расположен целиком внутри соленоида так, что одна его сторона лежит на оси. Пусть длина каждой из сторон контура равна L. Тогда 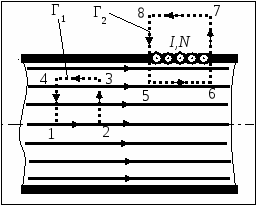 , ,(вычеркнуты нулевые слагаемые). Но контур не охватывает никакие токи, поэтому где I – сила тока, n – плотность намотки витков. Следовательно, магнитное поле внутри идеального соленоида является однородным. Теперь рассмотрим циркуляцию по квадратному контуру Г2, который расположен так, что одна его сторона лежит внутри соленоида параллельно оси, а противоположная - снаружи. Пусть длина каждой из сторон контура равна L. Этот контур охватывает витки, число которых равно N. По виткам текут одинаковые токи в одинаковом направлении, поэтому исходя из ориентации контура и направления токов, получаем Но При этом внутри соленоида У идеального соленоида магнитное поле сосредоточено только внутри соленоида. 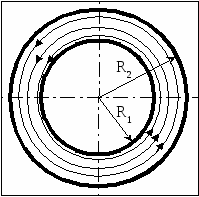 Тороид – это тонкий проводник, плотно намотанный на поверхность тора (бублика). Тороид – это тонкий проводник, плотно намотанный на поверхность тора (бублика).Магнитное поле тороида обладает осевой симметрией, поэтому силовые линии являются концентрическими окружностями с центрами на оси тороида. Пусть число витков в тороиде равно N, сила тока в проводнике равна I. Рассмотрим циркуляцию вектора индукции вдоль контура Г радиуса r ( |
