Лекция матрицы план Понятие матрицы. Типы матриц. Алгебра матриц
 Скачать 337.86 Kb. Скачать 337.86 Kb.
|
4.2 ОпределителиВычислить определители а) 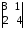 ; б) ; б) 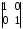 ; в) ; в) 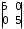 ; г) ; г) 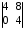 ; д) ; д) 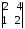 ; е) ; е) 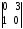 ; ; ж) 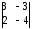 ; з) ; з) 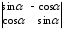 . .а) 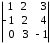 ; б) ; б) 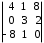 ; в) ; в) 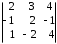 ; г) ; г) 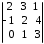 . .Вычислить определители примера 2, используя теорему Лапласа. Вычислить определители, предварительно упростив их: а) 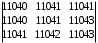 ; б) ; б) 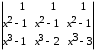 ; в) ; в) 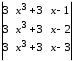 ; ;г) 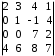 ; д) ; д) 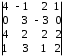 ; е) ; е) 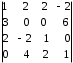 ; ;ж) 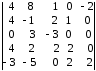 . .Вычислить определитель методом приведения его к треугольному виду 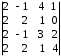 . .Пусть даны матрицы А и В. Доказать, что 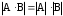 : :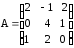 , , 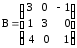 . .ОТВЕТЫ ПО ТЕМЕ «ОПРЕДЕЛИТЕЛИ»а) 10; б) 1; в) 25; г) 16; д) 0; е) –3; ж) -6; з) 1. а) –25; б) 168; в) 21; г) 12. а) –25; б) 168; в) 21; г) 12. 4. а) 2; б) 0; в) 0; г) 70; д) 18; е) –66; ж) -36. 5. –24. 4.3 Обратная матрицаНайти обратную матрицу: а) 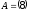 ; б) ; б) 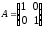 ; в) ; в) 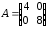 ; г) ; г) 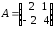 ; ; д) 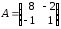 ; е) ; е) 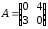 ; ж) ; ж) 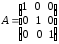 ; з) ; з) 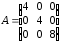 ; ;и) 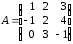 ; к) ; к) 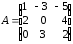 ; л) ; л) 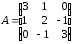 ; ;м) 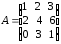 ; н) ; н) 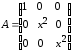 . .Найти обратную матрицу и проверить выполнение условия 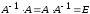 : :а) 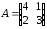 ; б) ; б) 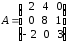 . .Доказать равенство 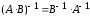 : :а) 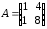 , , 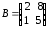 ; б) ; б) 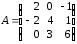 , ,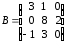 . .Доказать равенство 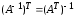 : :а) 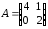 ; б) ; б) 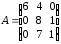 . .ОТВЕТЫ ПО ТЕМЕ «ОБРАТНАЯ МАТРИЦА»а) 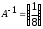 ; б) ; б) 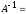 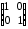 ; в) ; в) 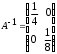 ; г) ; г) 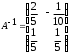 ; ;д)  ; е) ; е)  ; ж) ; ж)   ; ; з) 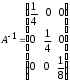 ; и) ; и) 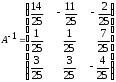 ; ; к) 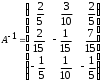 ; л) ; л) 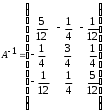 ; ;м) 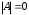 ; н) ; н) 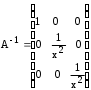 . .2. а) 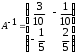 ; б) ; б) 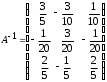 . .а) 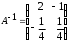 , , 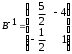 , , 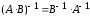 = =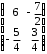 ; ;б) 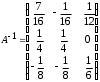 , , 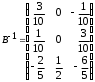 , ,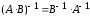 = =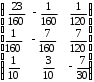 . .а) 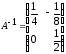 , , 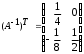 , , 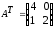 , , 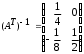 ; ;б) 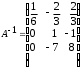 , , 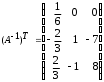 , , 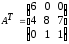 , , 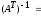 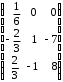 . .5. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ Вычислить определитель разложением а) по i- той строке; б) по j- тому столбцу. 1.1. 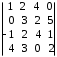 ; 1.2. ; 1.2. 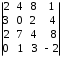 ; 1.3. ; 1.3.  ; ;i=2, j=3. i=4, j=1. i=3, j=2. 1.4. 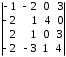 ; 1.5. ; 1.5. 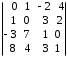 ; 1.6. ; 1.6.  ; ;i=3, j=3. i=1, j=4. i=2, j=2. 1.7. 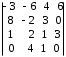 ; 1.8. ; 1.8. 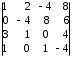 ; 1.9. ; 1.9. 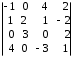 ; ;i=4, j=4. i=2, j=2. i=3, j=2. 1.10. 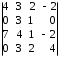 ; 1.11. ; 1.11. 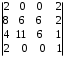 ; 1.12. ; 1.12. 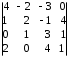 ; ;i=2, j=1. i=1, j=2. i=3, j=2. 1.13. 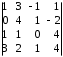 ; 1.14. ; 1.14. 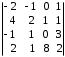 ; 1.15. ; 1.15. 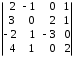 ; ;i=2, j=3. i=1, j=3. i=4, j=2. 1.16. 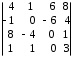 ; 1.17. ; 1.17. 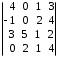 ; 1.18. ; 1.18. 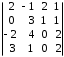 ; ;i=2, j=3. i=2, j=4. i=1, j=3. 1.19. 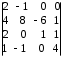 ; 1.20. ; 1.20. 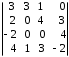 ; 1.21. ; 1.21. 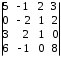 ; ;i=2, j=2. i=1, j=4. i=3, j=2. 1.22.  ; 1.23. ; 1.23. 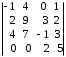 ; 1.24. ; 1.24. 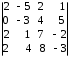 ; ;i=1, j=3. i=2, j=1. i=3, j=4. 1.25. 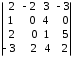 ; 1.26. ; 1.26. 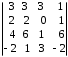 ; 1.27. ; 1.27. 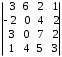 ; ;i=4, j=3. i=3, j=3. i=1, j=2. 1.28. 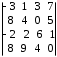 ; 1.29. ; 1.29. 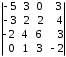 ; 1.30. ; 1.30. 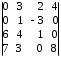 . .i=3, j=3. i=2, j=1. i=3, j=2. ЛИТЕРАТУРА Жевняк Р.М., Карпук А.А. Высшая математика. – Мн.: Выш. шк., 1992.- 384 с. Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Мн.: Тетрасистемс, 1998.- 288 с. Марков Л.Н., Размыслович Г.П. Высшая математика. Часть 1. –Мн.: Амалфея, 1999. – 208 с. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. I семестр. М.: Новое знание, 2002.- 140 с. Коваленко Н.С., Минченков Ю.В., Овсеец М.И. Высшая математика. Учеб. пособие. -Мн.: ЧИУП, 2003. – 32 с. 3 |
