1-лекция Модульдер және сақина. 1-лекция. Лекция Модульдер жне саина Категориялар теориясыны кейбір негізгі ымдары
 Скачать 31.52 Kb. Скачать 31.52 Kb.
|
|
1-лекция Модульдер және сақина 1.Категориялар теориясының кейбір негізгі ұғымдары 1945 жылдан бастап математиканың жаңа облысы – категориялар теориясы дами бастады. Бұл теория өте маңызды. Жаңа ұғымдар мен әдістерді әкелумен ғана қызықты емес, сонымен қатар математиканы толықтай түсінуге бағыттайды. Оның мәні маңызды ұғымдарды бірдей қамтып және математиканың әртүрлі бөлімдерін талқылауға мүмкіндік береді. Жеке жағдайда, ол әртүрлі құрылымдардың жалпы қасиеттерін зерттеп, оларды тұжырымдауға мүмкіндік береді. Категориялар теориясы өзімен бірге жаңа көзқарастармен қатар мәселелердің қойылуын әкеліп қана қойған жоқ, сонымен қатар тек қана өздерінде қызықты болып тұрғанымен әртүрлі нақты категорияларда жаңа зерттеулерді өмірге әкелді. Бұл әсіресе модульдер теориясына қатысты, ол өз кезегінде категориялар теориясының дамуына әкеп соқты. Сонымен бірге категориялар теориясының негізгі ұғымдары көп мөлшерде математикалық «сөйлеу тілінен» кіреді және математиканың басқа бөлімдерінде тұжырымдар мен ұғымдарды айтуға қолданады. Модульдер категорияларына осындай категориялық тілді білу міндетті. Біз мүмкіндігінше қысқа айтамыз, бірақ қарастырылып отырған ұғым оны ұғуға қанша керек болса, сонша алысқа дамиды. Категориялар туралы толық мағлұматты осы серия бойынша Б.Парайгисяның «Категория және функторлар» кітабынан таба аласыздар. Категорияның анықтамасы Біз жиын және класс ұғымдары белгілі деп есептейміз. Бірінші жуықтауда класс деп «өте үлкен жиынды» айтуға болады, оларға амалдар қолдануға болмайды, себебі ол қайшылыққа әкеліп тіреуі мүмкін. Мәселен, кластан барлық ішкі кластардың класын құруға болмайды, осындай жиынның барлық ішкі жиындарынан жиыны болады. Жиындардың аксиомалық теориясында және жиындар класында – бұл дәл сол кластар, олар қандай да бір кластың элементтері болып табылады. Интуитивті түрде класс дегеніміз қандай да бір қасиетке ие объектілердің барлық жиынтығы. Дәл мәліметтерді сәйкес оқулықтардан табуға болады, бұл жерде бұдан басқа айтылғандар қолданылмайды, себебі бұл кітапта класс ұғымына негізделген математикалық талдаулар қолданылмайды. Анықтама. К категориясы берілуі үшін келесі ұғымдар берілуі керек: Ob(K) класы, ол К категориясының объектілер класы деп аталады, оның элементтері К категориясының объектілері деп аталады. Олар А,В,С әріптерімен белгіленеді. MorK(A,B) жиыны үшін әрбір (A,B) жұбы (A,B)≠(С,D) әртүрлі жұп объектілері болғанда MorK(A,B)∩MorK(С,D)=  болады; болады;MorK(A,B) жиынының элементтері А-дан В-ға морфизмдер деп аталады, олар α, β, 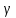 ... әріптерімен белгіленеді. ... әріптерімен белгіленеді.Объектілердің әрбір (A,B,С) үштігі үшін MorK(В,С)× MorK(A,B) 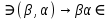 MorK(A,С) морфизмдер көбейту деп аталатын бейнелеуі (немесе композиция) үшін: MorK(A,С) морфизмдер көбейту деп аталатын бейнелеуі (немесе композиция) үшін: (1) ассоциативті заңы орындалады: 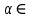 MorK(A,B), MorK(A,B), 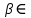 MorK(В,С), MorK(В,С), 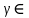 MorK(С,D) үшін MorK(С,D) үшін 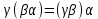 болады; болады;(2) тепе-тең морфизмдер табылады: А€ Ob(K) обьектісі үшін 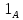 € € 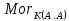 морфизмі табылып, ол А-ның тепе-тең морфизмі деп аталады, сонда әрбір α € морфизмі табылып, ол А-ның тепе-тең морфизмі деп аталады, сонда әрбір α €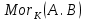 үшін α× үшін α×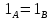 ×α ×α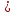 α болады. Енді қандайда бір белгілеулерді және қарапайым қасиеттерді келтіреміз. Егер шатаспасақ біз Mor(A.B) α болады. Енді қандайда бір белгілеулерді және қарапайым қасиеттерді келтіреміз. Егер шатаспасақ біз Mor(A.B)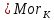 (A.B) деп белгілейміз. Әрі қарай Mor(K) (A.B) деп белгілейміз. Әрі қарай Mor(K)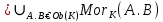 K категориясының барлық морфизмдер классын белгілейміз. Келесі қысқартылған жазулар қолданылады: А € К: 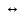 А€ Ob(K). Α € K: А€ Ob(K). Α € K: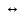 α € Mor(K). α € Mor(K).Енді α € Mor(A.B) болсын. Сонда бейнелеудегі сияқты келесіні анықтаймыз: α-ның анықталу облысы α 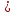 dom(α): dom(α):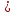 А, α-ның мәндер облысы А, α-ның мәндер облысы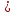 ran(α): ran(α):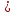 B. B.Mor(A.B) жиындары(А,В) әртүрлі жұптарында қиылыспайды, сондықтан dom(α) және ran(α) α морфизмі үшін бірмәнді түрде анықталады. Α € Mor(A.B) жазу орнына α: А 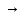 В немесе А В немесе А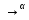 В деп жазады. А В деп жазады. А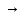 В жазуы Mor(A.B) жиынының қандай да бір элементін береді, ал В жазуы Mor(A.B) жиынының қандай да бір элементін береді, ал 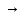 жебесі Mor(A.B) жиынының қандай да бір элементін береді. βα жебесі Mor(A.B) жиынының қандай да бір элементін береді. βα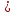 δγ жазуы диаграммасы коммутативті екенін көрсетеді: Егер α,β€ Mor(K) морфизмдері үшін βα деп жазсақ, ол ran(α) δγ жазуы диаграммасы коммутативті екенін көрсетеді: Егер α,β€ Mor(K) морфизмдері үшін βα деп жазсақ, ол ran(α)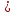 dom(β) шарты орындалғанын көрсетеді, яғни 1.1.1 анықтамасының талаптары орындалған. dom(β) шарты орындалғанын көрсетеді, яғни 1.1.1 анықтамасының талаптары орындалған.1.1.2 Тұжырым. 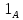 тепе-тең морфизмі Ⅲ(2) көрсетілген қасиет бойынша бірмәнді анықталады. тепе-тең морфизмі Ⅲ(2) көрсетілген қасиет бойынша бірмәнді анықталады. Дәлелі: Егер 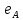 - тепе-тең морфизм болса, онда - тепе-тең морфизм болса, онда 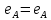 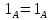 болады. болады.1.1.3. Анықтама. К- категория болсын және α:А→В – оның морфизмі, сонда: 1. Егер 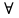 С С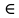 К К 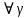 1, 1, 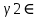 Mor(C, A) { α Mor(C, A) { α 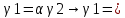 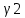 } болса, онда α – мономорфизм деп аталады; } болса, онда α – мономорфизм деп аталады;2. Егер 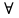 С С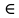 К К 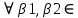 Mor(В, С) {p1 α =p2 α → p1=p2} болса, онда α – эпиморфизм деп аталады; Mor(В, С) {p1 α =p2 α → p1=p2} болса, онда α – эпиморфизм деп аталады;3. Егер (α - мономорфизм)˄( α - эпиморфизм) болса, онда α – биморфизм деп аталады; 4. Егер 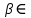 Mor(В, А) { Mor(В, А) { 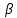 α =1А ˄ α α =1А ˄ α 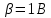 } болса, онда α – изоморфизм деп аталады. } болса, онда α – изоморфизм деп аталады.5. Егер dom(α)=ran(α) болса, онда – эндоморфизм деп аталады; 6. Егер (α - изоморфизм)˄( α - эндоморфизм) болса, онда α – автоморфизм деп аталады. 1.1.4. Тұжырым (α - изоморфизм)˄( α - биморфизм) Дәлелі: 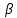 α =1А және α α =1А және α 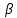 = 1В болып, сонда α = 1В болып, сонда α 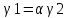 болса, онда болса, онда 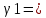 1А 1А 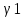 = = 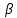 α α 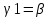 α α 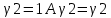 болады. болады.Дәлелі: 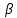 1α = 1α = 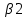 α болса, онда α болса, онда 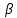 1= 1= 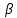 1 1В= 1 1В= 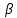 1 α 1 α 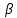 = = 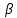 2 α 2 α 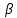 = = 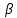 2 1В= В2 болады. 2 1В= В2 болады.1.1.4 Кері тұжырым жалпы алғанда орындалмайды. Бірақ ол бірқатар маңызды категорияларда, мәселен, модульдер категориясына ақиқат; кейін біз оны көрсетеміз. 1.2. Категориялар мысалдары Төменде көрсетілген мысалдарда (I) пунктінде обьектілер класы, ал (II) – Mor(A,B) жиыны, (III) – морфизмдер көбейтіндісі. Әркезде аксиомалар жеңіл тексеріледі. 1.2.1. 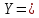 жиындар категориясы ( жиындар категориясы (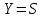 әріпі) әріпі)(І) 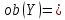 барлық жиындар класы. барлық жиындар класы.(ІІ) 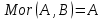 -дан B-ға барлық бейнелеулер жиыны. -дан B-ға барлық бейнелеулер жиыны.(ІІІ)  мен мен 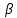 -ның композициясы (әуелі -ның композициясы (әуелі 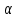 бейнелеу, сосын бейнелеу, сосын 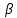 бейнелеуінің тізбектей орындалуының нәтижесі) бейнелеуінің тізбектей орындалуының нәтижесі)1.2.2. G= (категория групп) топтар теориясы. (І) 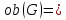 барлық жиындар класы. барлық жиындар класы.(ІІ) 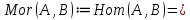 A-дан B-ға барлық топтың гомоморфизмдер жиыны. A-дан B-ға барлық топтың гомоморфизмдер жиыны.(ІІІ) Композиция. 1.2.3. 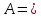 абельдік топтар категориясы. абельдік топтар категориясы.(І) 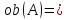 барлық абельдік топтар класы. барлық абельдік топтар класы.(ІІ) және (ІІІ) тура 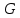 -дағы сияқты. -дағы сияқты. Бұл мысалда 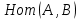 жиынының өзін абельдік топқа айналдыруға болады. жиынының өзін абельдік топқа айналдыруға болады. Анықтама.B-дағы топтық амал аддитивті түрде жазылсын, және 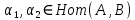 болсын. болсын. 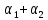 бейнелеуін келесі түрде анықтаймыз: бейнелеуін келесі түрде анықтаймыз: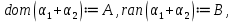 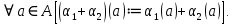 Сонда 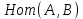 осы кезде абельдік топ болатыны жеңіл тексеріледі. Жеке жағдайда оның нөлдік элементі болып А-дан В-ға нөлдік бейнелеу болады, және әрбір осы кезде абельдік топ болатыны жеңіл тексеріледі. Жеке жағдайда оның нөлдік элементі болып А-дан В-ға нөлдік бейнелеу болады, және әрбір 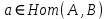 үшін – үшін – 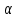 келесі түрде анықталады. келесі түрде анықталады. 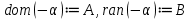 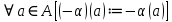 1.2.4. 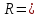 бірлік элементі бар сақиналар категориясы. бірлік элементі бар сақиналар категориясы. (І) 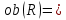 бірлік элементі бар сақиналар класы. бірлік элементі бар сақиналар класы.(ІІ) 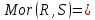 барлық унитарлық сақиналық гомоморфизмдер класы ( барлық унитарлық сақиналық гомоморфизмдер класы (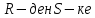 ). (3.2.1 анықтаманы қара). ). (3.2.1 анықтаманы қара). (ІІІ) Композиция. 1.2.5 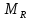 = бірлік элементі бар R сақинасындағы унитарлы оң R-модульдер сақиналар категориясы = бірлік элементі бар R сақинасындағы унитарлы оң R-модульдер сақиналар категориясы (I) Ob( 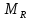 )=унитарлы оң R-модульдер класы (2.1.1 анықтамасы) )=унитарлы оң R-модульдер класы (2.1.1 анықтамасы)(II) Mor(A,B)= 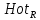 (A,B)=А-дан В-ға модульдік R гомоморфизмдер жиыны (A,B)=А-дан В-ға модульдік R гомоморфизмдер жиыны(III) Композиция. Абельдік топтар категориясы сияқты, 1.2.3 анықтамасы бойынша, 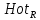 (A,B) абельдік топқа айналады, бірақ, жалпы айтқанда R-модуль болмайды! Ол туралы кейін тарқатып айтылады. (A,B) абельдік топқа айналады, бірақ, жалпы айтқанда R-модуль болмайды! Ол туралы кейін тарқатып айтылады. Егер S- тағы да бір бірлік элементке ие сақина болсак, онда және 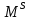 және және 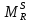 арқылы, сәйкесінше, унитарлы сол жақ S-модульдер және унитарлы S-R-бимодульдер категорияларын белгілейді (2.1.1 анықтамасы және содан кейінгі абзацты қараңыз). арқылы, сәйкесінше, унитарлы сол жақ S-модульдер және унитарлы S-R-бимодульдер категорияларын белгілейді (2.1.1 анықтамасы және содан кейінгі абзацты қараңыз).1.2.6 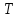 =топологиялық кеңістіктер категориясы. =топологиялық кеңістіктер категориясы.(I) Ob( 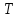 ) = барлық топологиялық кеңістіктер класы. ) = барлық топологиялық кеңістіктер класы.(II) Mor(A,B) =А-дан В-ға барлық үзіліссіз бейнелеулер жиыны. (III) Композиция. Қарастырылған категориялардың барлық мысалдарында 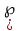 басқа) обьектілер ретінде қосымша құрылымы бар жиындар қарастырылып, ал морфизмдер ретінде осы құрылымды сақтайтын бейнелеулер алынды. Енді біз басқа түрдегі категория мысалдарын келтіреміз. басқа) обьектілер ретінде қосымша құрылымы бар жиындар қарастырылып, ал морфизмдер ретінде осы құрылымды сақтайтын бейнелеулер алынды. Енді біз басқа түрдегі категория мысалдарын келтіреміз. 1.2.7 Топ категория ретінде. 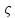 – кез-келген топ болсын және * - оның кез-келген элементі. – кез-келген топ болсын және * - оның кез-келген элементі. (I) Ob( 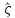 ) = {*} ) = {*}(II) Mor(*,*) = 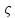 (III) 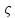 – дағы топтық амал. – дағы топтық амал. 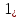 = = 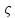 тобының нейтральді элементі екені түсінікті. тобының нейтральді элементі екені түсінікті.1.2.8. Реттелген жиын категория ретінде (M, ≤) – реттелген жиын болсын, М категориясын келесі түрде анықтаймыз: (I) Ob(Ḿ) = M (II) Mor(A,B): 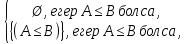 яғни 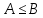 болған жағдайда Mor(A,B) жиыны (A болған жағдайда Mor(A,B) жиыны (A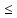 B) жалғыз символынан тұратын жиын болады. B) жалғыз символынан тұратын жиын болады.(III) (B 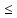 C) (A C) (A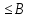 ): = (A ): = (A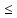 C) C)A үшін тепе-тең морфизм 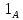 =(A =(A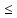 A) болады. A) болады.1.2.9. Дуальді категория Kкатегориясы берілсін, К категориясына дуальді 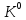 категориясы келесі түрде анықталады. категориясы келесі түрде анықталады.(I) Ob(K 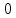 ) = Ob(K) ) = Ob(K)(II) 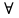 A,B A,B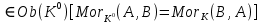 (III) 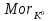 (B,C) x (B,C) x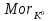 (A,B) (A,B)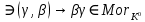 (A,C), мұндағы (A,C), мұндағы 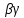 морфизмі Mor(K) пайда болады. морфизмі Mor(K) пайда болады.1.3. Функторлар Функторлар категориялар үшін алгебралық құрылымдарда құрылымды сақтайтын бейнелеулер (гомоморфизмдер) сияқты немесе топологиялық құрылымдарда үзіліссіз бейнелеулер сияқты роль атқарады. Осы сәйкестікке байланысты функтор (біздің анықтамамызда) – бұл бір категориядан басқа категорияға бейнелеулердің құрылымын сақтайтын жұп (бұл жерде категориялар бір-бірінен бөлек болмауы да мүмкін). 1.3.1. Ковариантты, сәйкесінше, контравариантты F функторы деп K категориясын L категориясына бейнелейтін 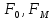 бейнелеулерінің F=( бейнелеулерінің F=(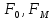 ) жұбын айтамыз, мұндағы ) жұбын айтамыз, мұндағы(I) 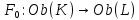 (II) 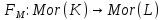 бейнелеулері келесі қасиеттерге ие: бейнелеулері келесі қасиеттерге ие:∀ α ϵ Mor (K) [α ϵ Mor (A,B) => F(m) (α) ϵ Mor (F(0)(A), F(0)(B))], сәйкесінше, [α ϵ Mor (A,B) => F(M) (α) ϵ Mor (F(0)(B), F(0)(A))]; ∀ A ϵ Ob (K) [F(m)(1a) =1(F0(A)]; ∀ α,β ϵ Mor (K) [ran(α) = dom(β) => Fm(βα) = Fm(β)Fm(α)], сәйкесінше [ ran(α) = dom(β) => Fm(βα) = Fm(α) Fm(β)]. F0 мен Fm орындарына жай ғана F деп жазады, яғни F(A) = F0(A), F(α) = Fm(α) сонда (1) шарты келесі түрге көшеді: (1) α:A -> B=> F(α): F(A) -> F(B), сәйкесінше α: A -> B => F(α) : F(β) -> F(A), немесе (1) dom (F(α)) = F (dom(α)) ∩ ran(F(α)) = F (ran(α)), сәйкесінше dom (F(α)) = F (ran(α)) ∩ ran(F(α)) = F (dom (α)). F: K -> I жазуы К-дан I-ге F фуниторы деген сөз. Егер С: I-> Р – тағыда функтор болса, онда олардың тізбектеу орындалуы СF: K->Р – тағыда функтор болады. Егер екі функтор F және С ковариантты немесе контровариантты болса, онда СF коварианты; егер F пен С әртүрлі «вариантты» болса, онда СF контровариантты болады. 1.3.2 Ұмытатын функторлар. Ұмытатын функтор F M® – ден А абельдік топтар категориясына келесі түрде анықталады: F0: Ob M® э A -> A Ob(A), FM: Mor M® э α -> α ϵ Mor(A) Бұл инвариантты функтор модульдік құрылымды «ұмытады», ол модульдік тек аддитивті құрылымын ғана сақтайды. Егер, сонымен, бірге аддитивті құрылымда «ұмытылатын» болса, онда M® нен I жиындар категориясына F ұмытатын функтор алынады: F0: Ob M® э A -> A Ob(I), FM: Mor M® э α -> α ϵ Mor(I). Функтордың қасиеттері айқын түрде тексеріледі. Ұмытатын функторлардың басқада мысалдарын келтіру оңай. 1.3.3. Қойылымдар функторлары. 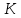 - кез-келген категория, ал А - кез-келген категория, ал А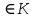 болсын. Келесі морфизмдерді анықтаймыз: болсын. Келесі морфизмдерді анықтаймыз: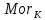 (A,-): Ob( (A,-): Ob(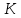 ) )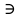 X X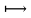 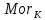 (A,X) (A,X)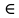 Ob( Ob(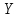 ), ),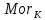 (A,-): Mor( (A,-): Mor(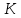 ) )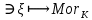 (A, (A,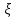 ) ) 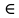 Mor( Mor(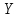 ), ),Мұндағы Х:=dom( 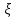 ), ),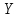 :=ran( :=ran(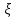 ) үшін ) үшін 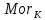 (A, (A,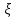 ) келесі түрде беріледі: ) келесі түрде беріледі: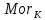 (A, (A,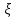 ): ): 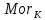 (A,X) (A,X)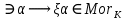 (A, (A, 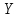 ). ).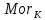 (A,-) – (A,-) – 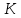 -дан -дан 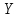 -ға ковариантты функтор екені айқын. -ға ковариантты функтор екені айқын.Дәл солай, В 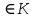 бекітілген объектісі, келесі морфизмдерді анықтаймыз: бекітілген объектісі, келесі морфизмдерді анықтаймыз: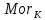 (-,B): Ob( (-,B): Ob(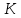 ) )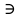 X X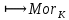 (X,B) (X,B)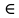 Ob( Ob(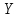 ), ),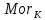 (-,B): Mor( (-,B): Mor(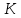 ) )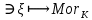 ( (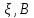 ) ) 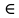 Mor( Mor(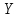 ), ),Мұндағы, Х:=dom( 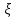 ), ), 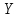 :=ran( :=ran(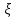 ) үшін ) үшін 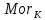 ( (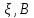 ) келесі түрде анықталады: ) келесі түрде анықталады: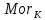 ( (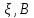 ): ): 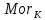 ( (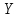 ,B) ,B)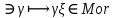 (X, (X, 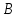 ). ).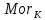 ( (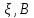 ) – ) – 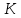 -дан -дан 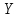 -ға контравариантты функтор тексеру қиын емес. -ға контравариантты функтор тексеру қиын емес.Осыған дейін біз бір аргументті функторларды қарастырдық, яғни бір категориядан екіншіге. Бірақ, көп аргументті функторлар жиі кездеседі. Дегенмен де категориялардың жұптасуы арқылы (дуальді категориялардың) олар бір аргументті функторға (ковариантты) келіп тіреледі. Біздің мақсатымыз үшін екі аргументті фнкторларды қарастырсақ жеткілікті. 1.3.4. Определение. К, 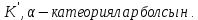 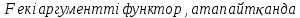 ковариантты, сәйкесінші, бірінші аргумент бойынша контравариантты, ал екінші аргумент бойынша ковариантты болсын, ол K* ковариантты, сәйкесінші, бірінші аргумент бойынша контравариантты, ал екінші аргумент бойынша ковариантты болсын, ол K*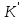 -тен -тен 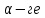 F=( F=(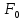 , , 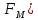 бейнелеулер жұбы: (I) бейнелеулер жұбы: (I) 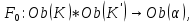 (II) (II) 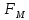 : Mor(K)*Mor( : Mor(K)*Mor(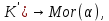 ол келесі қасиеттерге ие: (1) ол келесі қасиеттерге ие: (1) 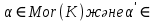 Mor( Mor(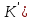 үшін, мұндағы үшін, мұндағы 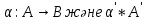 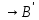 бейнелейді, бейнелейді, 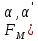 ): ):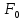 (A, (A, 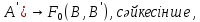 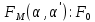 (B, (B, 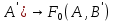 (2) (2) 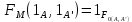 ; (3) ; (3) 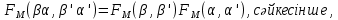 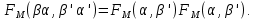 Дәл солай екі аргумент бойынша контравариантты немесе бірінші аргумент бойынша ковариантты және екінші аргумент бойынша контравариантты функтор анықталады. Дәл солай екі аргумент бойынша контравариантты немесе бірінші аргумент бойынша ковариантты және екінші аргумент бойынша контравариантты функтор анықталады. 1.3.5. Mor Функторы. Әрбір К категориясына Mor= 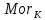 функторы сәйкес келеді, ол К функторы сәйкес келеді, ол К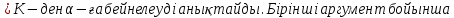 контравариантты . Ол келесі түрде анықталады : Mor: Ob(K)* Ob(K) контравариантты . Ол келесі түрде анықталады : Mor: Ob(K)* Ob(K)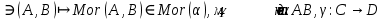 үшін Mor(α, үшін Mor(α,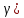 келесі түрде анықталады: Mor( келесі түрде анықталады: Mor(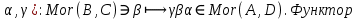 қасиеттері жеңіл тексеріледі. Осы функтордың жеке жағдайы ретінде Hom функторын аламыз: қасиеттері жеңіл тексеріледі. Осы функтордың жеке жағдайы ретінде Hom функторын аламыз: 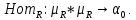 |
