Лекция. Лекция по теме Магнитные цепи

• Название: Лекция по теме Магнитные цепи
• Дата: 14.01.2022
• Размер: 186.53 Kb.
• Имя файла: Лекция.docx
• Тип: Лекция; #330687

^Лекция по теме: «Магнитные цепи»

Цель: изучение основ теории магнитных цепей, электротехнических и электронных устройств, приобретение определенных навыков по расчету магнитных цепей.

Магнитная цепь – совокупность тел и сред, представляющих собой путь, по которому замыкается магнитный поток.

Основной величиной, характеризующей интенсивность и направление ^{магнитного поля является – вектор магнитной индукции , которая} измеряется в Теслах [Тл].

Второй важной величиной, характеризующей магнитное поле является –

^{магнитный поток , который измеряется в Веберах [Вб].}

Магнитные цепи

Всякий электромагнит состоит из стального сердечника – магнитопровода и намотанной на него катушки с витками изолированной проволоки, по которой проходит электрический ток.

Совокупность нескольких участков: ферромагнитных (сталь) и неферромагнитных (воздух), по которым замыкаются линии магнитного потока, составляют магнитную цепь.

Закон полного тока

В основе расчета магнитных цепей лежит закон полного тока
,

где: Н – напряженность магнитного поля в данной точке пространства; dL – элемент длины замкнутого контура L; ^{α – угол между направлениями векторов 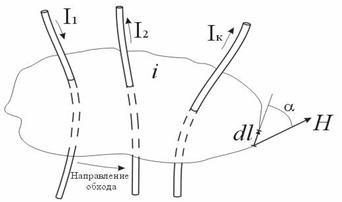и ;} I – алгебраическая сумма токов, пронизывающих контур L.

Рис. Закон полного тока

Ток I_к, пронизывающий контур L считается положительным, если принятое направление обхода контура и направление этого тока связаны правилом правоходового винта (буравчика).

Применение закона полного тока для расчета магнитных цепей

Рассмотрим простейшую магнитную цепь, выполненную в виде кольца тороида из однородного материала.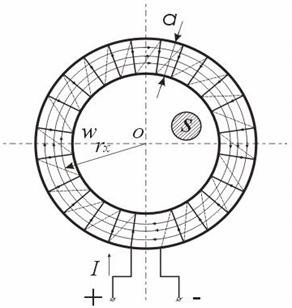



Рис. Кольцевая магнитная цепь

Обмотка имеет W витков и обтекается током I. Магнитные линии внутри кольца представляют собой концентрические окружности с центром в точке О. Применим к контуру C_х, совпадающему с одной из магнитных линий, проходящих в магнитопроводе, закон полного тока. При этом будем считать:

и совпадают, следовательно α = 0; величина Нх во всех точках контура одинакова; сумма токов, пронизывающих контур, равна IW.

Тогда
.

Отсюда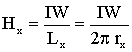

[А/м],

где L_x – длина контура, вдоль которого велось интегрирование; r_x – радиус окружности.

^{Вектор внутри кольца зависит от расстояния rх. Если α – ширина} кольца << d, то эта разница между значениями Н в пределах сердечника не велика. При этом в расчет допустимо принять для всего поперечного сечения магнитопровода одно значение напряженности магнитного поля:

H_ср = IW / L ,

где L – длина средней магнитной линии.

Закон Ома для магнитной цепи. Линейные и нелинейные магнитные сопротивления

В кольцевом магнитопроводе с равномерной обмоткой все поле концентрируется внутри кольца.

Определим в этом случае магнитный поток в магнитопроводе с распределенной обмоткой.

Исходя из соотношений Ф = B_ср S и B_ср = μ_а H_ср получим

Ф = B_ср S = μ_а H_ср S .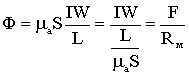




Магнитный поток Ф зависит от произведения IW = F, которое получило название магнитодвижущей силы (МДС).

Величину L / (μ_а S) = R_м – принято назвать магнитным сопротивлением магнитопровода (по аналогии с электрическим сопротвлением r = L / γ S).

Магнитное сопротивление воздуха (зазоров) линейное, т.к. μ_а = μ_o = const. Магнитное сопротивление сердечника нелинейно – μ_а зависит от В.

Если намагничивающую силу F, уподобить действию ЭДС, будет получено соотношение, похожее на выражение закона Ома для цепи постоянного тока. В связи с этим формулу принято назвать законом Ома для магнитной цепи. Следует оговориться, что эта аналогия – формальная, а физическая сущность процессов в электрических и магнитных цепях различна.

Ферромагнитные материалы и их свойства

Известно, что магнитная проницаемость μ_а ферромагнитных материалов переменная величина и зависит от В. Это влечет за собой непостоянство магнитного сопротивления R_м и значительно усложняет расчеты магнитных цепей. Поэтому для расчета магнитных цепей, содержащих ферромагнитные участки, необходимо располагать кривыми намагничивания, представляющими собой зависимость B = f(H). Эти зависимости получают экспериментальным путем – испытанием замкнутых магнитопроводов с распределенной обмоткой.

Первоначальному намагничиванию образца соответствует кривая, называемая кривой первоначального намагничивания.

Если образец подвергать циклическому намагничиванию при изменении напряженности магнитного поля в пределах +Н_х до –Н_х, то график будет представлять замкнутую кривую, известную под названием петли гистерезиса.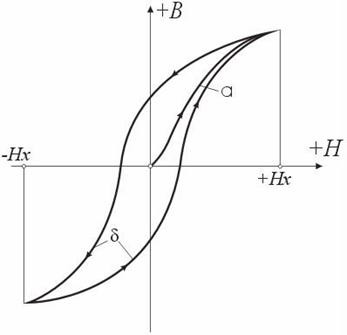



Рис. Зависимость В(Н) – петля гистерезиса

Если процесс циклического намагничивания повторять для постепенно увеличивающихся значений напряженности магнитного поля, то можно получить семейство петель гистерезиса, и так называемую предельную петлю гистерезиса, которой соответствует изменение напряженности магнитного поля в пределах от +Н_max до –Н_max, увеличение Н сверх Н_max не повлечет за собой увеличение площади петли гистерезиса. Предельная петля гистерезиса определяет значение остаточной магнитной индукции и коэрцетивной силы Н_с. Кривая, соединяющая вершины петель гистерезиса, называется основной кривой намагничивания. Эти кривые приводятся в справочных руководствах и используются в расчетах магнитных цепей.

Процесс циклического перемагничивания требует затраты энергии, как известно из курса физики, пропорциональной площади петли гистерезиса.

В связи с этим магнитопроводы электротехнических устройств, работающих в условиях непрерывного перемагничивания (например трансформаторы), целесообразно выполнять из ферромагнитных материалов, имеющих узкую петлю гистерезиса. Такие ферромагнитные материалы называют магнитомягкими (листовая электротехническая сталь и ряд специальных сплавов, например пермаллой, состоящий из никеля, железа и других компонентов).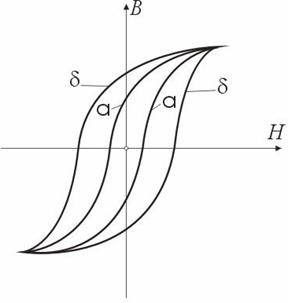



Рис. Петли гистерезиса магнитомягих (кривые α) и магнитотвердых (кривые δ) материалов

Для изготовления постоянных магнитов рекомендуется использовать ферромагнитные материалы с широкой петлей гистерезиса (кривые δ), имеющих большую остаточную индукцию и большую коэрцетивную силу. Такие ферромагнитные материалы называют магнитотвердыми (ряд сплавов железа с вольфрамом, хромом и алюминием.

Особенности расчета магнитных цепей с переменной магнитодвижущей силой

Физические процессы в цепях переменного тока, содержащих катушку со стальным сердечником, имеют ряд особенностей по сравнению с процессами в цепях постоянного тока. Эти особенности оказывают существенное влияние на конструктивное выполнение и технические характеристики электрических аппаратов и машин переменного тока.

Ферромагнитные элементы в цепях переменного тока имеют дополнительные потери в сердечнике на гистерезис и вихревые токи. Для снижения потерь стальной сердечник выполняют шихтованным из тонких изолированных друг от друга пластин.

Потери в сердечнике

Потери в сердечнике, называемые потерями в стали Р_с, увеличиваются при повышении частоты питающего напряжения. Переменный магнитный поток Ф индуктирует в стальном сердечнике вихревые токи (токи Фуко), замыкающиеся в плоскостях, перпендикулярных к оси потока. Эти токи вызывают нагрев стали, снижая тем самым КПД и ограничивая нагрузочную способность электромагнитных устройств. Потери энергии в стальном магнитопроводе значительно снижаются при уменьшении толщины листа электротехнической стали

Помимо потерь от вихревых токов, в стальном магнитопроводе при переменном магнитном потоке возникают потери, обусловленные явлением гистерезиса

P_г = k_г f B_m² G ,

где k_г – постоянный коэффициент;

G – вес сердечника в килограммах.

Суммарные потери от вихревых потоков и гистерезиса P_с = P_в + P_г [Вт] называют магнитными потерями или потерями в стали.

Правило Ленца

Правило Ленца - правило для определения направления индукционного тока: индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток. Сформулировано в 1833 г. Э. Х. Ленцем.

Если ток увеличивается, то и магнитный поток увеличивается.

В обобщенной формулировке правило Ленца гласит, что возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которое вызвалоэтотток.

Явление электромагнитной индукции.

Закон Фарадея

1. 
   Опыты Фарадея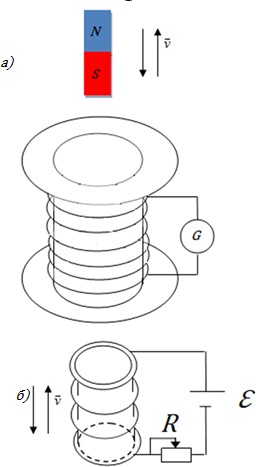
   

а) В соленоид, замкнутый на гальванометр, вдвигается и выдвигается постоянный магнит. На гальванометре будет отклонение стрелки, и оно будет тем больше, чем быстрее происходит вдвижение и выдвижение. При изменении полюсов магнита направление отклонения стрелки изменится.

б) В соленоид, замкнутый на гальванометр, вставлена катушка (другой соленоид), через которую пропускается ток. При включении и выключении (т.е. при любом изменении тока) происходит отклонение стрелки гальванометра.

Направление отклонения изменяется при включении – выключении, уменьшении – увеличении тока, вдвигании – выдвигании катушек.

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает индукционный (наведенный) электрический ток.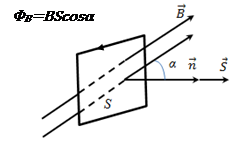




Возникновение индукционного тока означает, что в контуре действует электродвижущая сила I – ЭДС индукции.

ЭДС индукции, возникающая в проводящем контуре, равна скорости изменения магнитного потока через площадь, ограниченную этим контуром

– закон Фарадея

В 1834 г. Э.Х. Ленц установил закон, позволяющий определить направление индукционного тока.

Правило Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.

Знак минус в законе Фарадея является математическим выражением правила Ленца.

Если контур, в котором индуцируется ЭДС, состоит не из одного витка, а из Nвитков (например, соленоид), то если витки соединены последовательно, Е_i будет равна сумме ЭДС, индуцируемых в каждом из витков в отдельности:



- потокосцепление или полный магнитный поток.




Если Ф₁=Ф₂=…=Ф_n, то




Т.к. Ф_B=BScosα,то для того чтобы изменить магнитный поток Фможно изменить:

1. 
   ^{магнитное поле ;}
   
2. 
   площадь S;
   
3. 
   угол α.
   

Вращение рамки в магнитном поле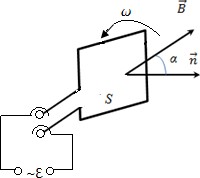

Явление электромагнитной индукции используется для преобразования механической энергии и энергии электрического тока в генераторах.

Рамка площадью S вращается в однородном ^{магнитном поле ( ) равномерно с}

постоянной угловой скоростью ω.

α = ωt. Тогда
При sin ωt=1




и



^{Т.к. частота сети , то для увеличения нужно} увеличивать Ви S. Вможно увеличить, применяя мощные постоянные

магниты, или в электромагнитах пропускать большие токи. Сердечник электромагнита выбирают с большим µ. Для увеличения Sиспользуют многовитковые обмотки.

Если через рамку, помещенную в магнитном поле, пропускать электрический ток, то на нее будет действовать вращающий момент



и рамка начнет вращаться. На этом принципе основана работа электродвигателей, предназначенных для превращения электрической энергии в механическую.

Токи Фуко.

Индукционные токи могут возбуждаться и в сплошных массивных проводниках. В этом случае их называют токами Фуко или вихревыми токами. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко могут достигать очень большой силы.

Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного поля, индуцирующего вихревые токи. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это используют для демпфирования (успокоения) подвижных частей гальванометров, сейсмографов и т.п. Тепловое действие токов Фуко используется в индукционных плавильных печах.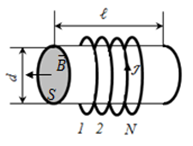



Для уменьшения токов Фуко сердечники трансформаторов делают из отдельных пластин и пластины перпендикулярны токам Фуко.

Вследствие возникновения вихревых токов быстропеременный ток неравномерно распределен по сечению провода - он вытесняется на поверхность проводника - скин-эффект. Поэтому на высоких частотах используют полые провода.

Индуктивность контура. Самоиндукция

В любом случае, когда по контуру протекает электрический ток, создается магнитное поле. При этом всегда имеется магнитный поток Ф, проходящий через поверхность, ограниченную рассматриваемым контуром. Любое изменение силы тока в контуре приводит к изменению магнитного поля, сцепленного с контуром, а это в свою очередь вызывает появление индукционного тока. Это явление получило название явления самоиндукции: возникновение ЭДС индукции в проводнике при изменении в нем тока.

Из закона Био-Савара-Лапласа следует




т.е. магнитный поток, сцепленный с контуром, пропорционален току Iв контуре

Ф=LI.

[L] = Гн (Генри). 1 Гн - индуктивность такого контура, магнитный поток самоиндукции которого при токе 1 А равен 1 Вб.

Рассчитаем индуктивность Lсоленоида:



магнитная индукция Всоленоида




^{т.е. индуктивность зависит от геометрических размеров соленоида ( ),}

числа витков и магнитной проницаемости сердечника соленоида.

Поэтому можно сказать, что индуктивность Lаналог емкости С уединенного проводника, которая также зависит от геометрических размеров, от формы и диэлектрической проницаемости среды.

Применяя к явлению самоиндукции закон Фарадея, получим, что ЭДС самоиндукции



Если L=const




где знак минус, обусловленный правилом Ленца, показывает, что наличие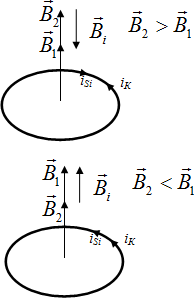

индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток

^{со временем возрастает, то , и}

т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником и тормозит его возрастание. Если ток со

^{временем убывает, то и т.е.} индукционный ток имеет такое же

направление, как и убывающий ток в контуре, и замедляет его убывание.

Следовательно, контур, обладающий индуктивностью, имеет

электрическую инертность, заключающуюся в том, что любое изменение тока тормозится, тем сильнее, чем больше индуктивность контура.