МУ Лабораторная работа 1-6 (1-12) (1). Определение коэффициента восстановления и энергии остаточной диформации при ударе тел
 Скачать 191 Kb.
|
|
Лабораторная работа № 1-6 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВОССТАНОВЛЕНИЯ И ЭНЕРГИИ ОСТАТОЧНОЙ ДИФОРМАЦИИ ПРИ УДАРЕ ТЕЛ ЦЕЛЬ РАБОТЫ: изучение закона сохранения энергии на примере удара твердых тел. Постановка экспериментальной задачиУдар твердых тел - совокупность явлений, возникающих при столкновении движущихся тел. Промежуток времени, в течение которого происходит удар, обычно очень мал (10-3 - 10-6 с). Во время удара тела деформируются, в зоне контакта возникают, так называемые, ударные силы, что приводит к значительным изменениям скоростей точек соударяющихся тел. Следствием удара могут быть остаточные деформации, звуковые колебания, нагревания тел, изменение механических свойств их материалов, а при скоростях соударения, больших, так называемых критических, наблюдается разрушение тел в месте удара. Характер протекания удара существенно зависит от модуля упругости, твердости, вязкости и других свойств материалов, от масс и размеров тел. В качестве меры механического взаимодействия тел при ударе служит импульс силы, т.е. величина  (1)где Fcp- средняя сила удара;  - время удара.Если импульс (количество движения) за время удара t изменяется на конечную величину  , то из второго закона Ньютона получим: (2)Рассеяние механической энергии при ударе характеризуется коэффициентом восстановления скорости К. Коэффициент восстановления скорости в случае центрального удара двух тел определяется:  (3)где  - скорости соударяющихся тел до удара;  - скорости тел после удара.В данной работе одно из взаимодействующих тел неподвижно, поэтому  и коэффициент восстановления: (4)или опуская индексы  (5)Для абсолютного упругого удара К = 1, для абсолютно неупругого – К = 0; в реальных случаях 0 < K < 1. Величина коэффициента восстановления К зависит от физических свойств материалов соударяющихся тел, от их формы, а также зависит от масс соударяющихся тел. В настоящей работе рассматриваются удар шара массой m, подвешенного в виде маятника, с неподвижным массивным телом в виде куба (рис.1). 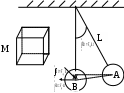 Рис.1В реальных условиях удар является частично упругим, поэтому кинетическая энергия движущегося шара  до удара превращается в кинетическую энергию шара после удара  и энергию остаточной деформации WОД взаимодействующих тел: (6)Отсюда, учитывая формулу (6), энергия остаточной деформации равна:  (7)Из формулы (7) следует, что при абсолютно упругом ударе (К = 1) энергия остаточной деформации равна нулю, т.е. механическая энергия не переходит в другие виды энергии. При абсолютно неупругом ударе (К = 0) кинетическая энергия шара полностью переходит в механические виды энергии, главным образом в энергию остаточной деформации. В этом случае WОД имеет максимальное значение, равное .Пусть шар массой m первоначально отклонен на угол 0 (рис.1). В точке А он обладает потенциальной энергией  , а кинетическая энергия его равна нулю. При движении шара его потенциальная энергия переходит в кинетическую энергию, которая при прохождении положения равновесия (точки В) становится максимальной и равной  , а потенциальная обращается в нуль.Тогда закон сохранения энергии запишется  или  .Отсюда  . (8)Из рис.1 видно, что ,где L - длина подвеса. Тогда (9)Соотношение (9) определяет скорость шара непосредственно перед ударом. Процесс удара протекает в две стадии. На первой стадии происходит деформация соударяющихся тел, их кинетическая энергия при этом переходит в потенциальную энергию деформации. На второй стадии удара происходит восстановление формы деформированных тел. Потенциальная энергия упругой деформации переходит в кинетическую энергию шара, эта энергия возвращающегося шага будет меньше его начальной кинетической энергии на величину остаточной деформации WОД. Вследствие этого скорость шара после удара будет меньше скорости до удара меньше скорости до удара и высота подъема его после удара будет меньше начальной высоты h0. Отсюда и угол отклонения после удара меньше начального угла 0. По аналогии (9), скорость u после удара равна:  (10)Подставив (9) и (10) и (5), найдем коэффициент восстановления: 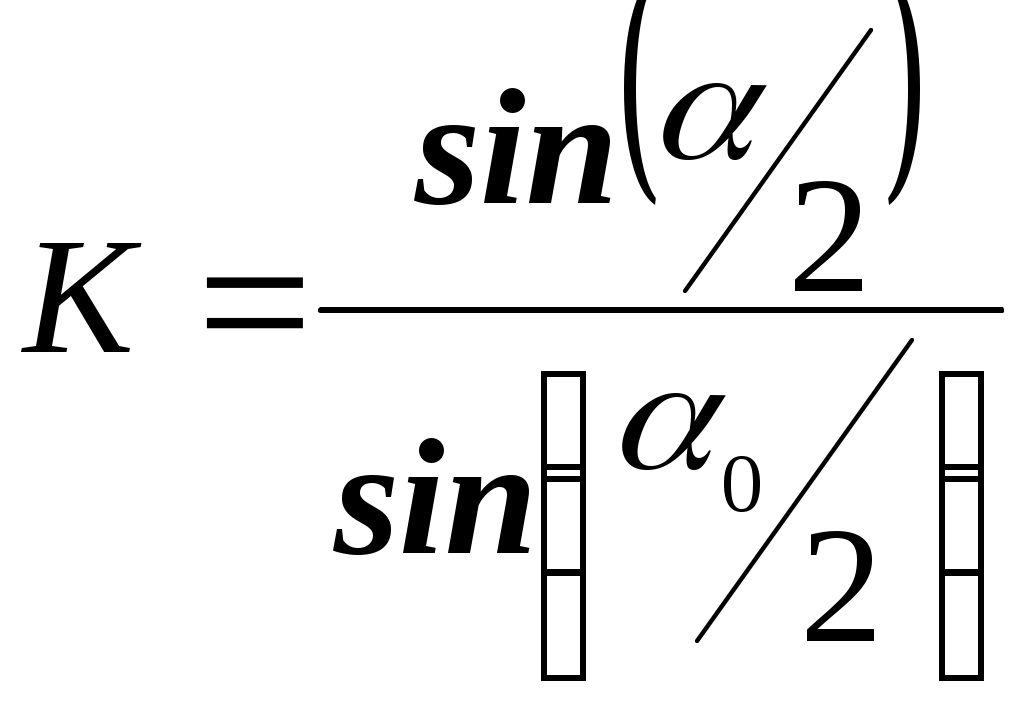 (11)Используя (7), (9) и (11), получим выражения для энергии остаточной деформации:  (12)Формулы (11) и (12) позволяют определить коэффициент восстановления К и энергию остаточной деформации WОД, если измерены углы 0 и и известны масса шара m и длина подвеса L. Описание установкиОбщий вид установки показан на рис.2. На основании 1 стойка 4, несущая подвески 5 шара 12 и штангу 7, на которой крепится электромагнит 8. Шар находится на металлическом бифилярном подвесе, который не позволяет ему выходить из вертикальной плоскости и вращаться вокруг радиальных осей. Электромагнит 8 служит для удержания шара в отклоненном положении. Шар может отводиться на угол в пределах 0 – 50 градусов от вертикального положения.  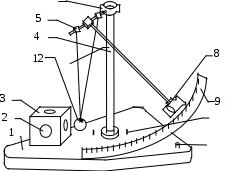 Рис.2Угол отсчитывается по шкале 9. На основании установки размещен куб 3 с укрепленными на нем образцами из различных материалов 2. Он обладает большой массой и служит неподвижной стеной для удара шара. Куб можно поворачивать вокруг вертикальной оси и фиксировать его грани перпендикулярно направлению удара. На основании также расположены клеймы для включения электромагнита в электрическую цепь и тумблер для управления работой электромагнита. Порядок выполнения работы1.Повернуть куб с исследуемым образцом и установить перпендикулярно направлению движения шара. 2.Включить источник постоянного тока, питающий электромагнит. 3.Подвести шар к электромагниту и включить тумблер “электромагнит”. 4.Установить шар в исходном положении под углом 30 – 40 градусов. 5.С помощью тумблера “электромагнит” освободить шар и отсчитать угол отклонения по шкале 9 после удара его с образцом. Измерения произвести 5 раз. Результаты занести в таблицу 1. 6.Найти среднее значение угла отклонения  .7.Пункты 1 - 6 повторить для каждого образца. 8.Вычислить коэффициент восстановления К по формуле (11) и энергию остаточной деформации WОД по формуле (12). 9.Рассчитать погрешности прямых измерений для одного образца. Результаты расчетов внести в таблицу 2. Таблица 1
Таблица 2
 10.Определить относительную и абсолютную погрешность измерений коэффициента восстановления К по формулам (  и  подставляются в радианах): , (13) (14)11.Записать окончательный результат и сделайте вывод о характере деформации образцов из различных материалов  WОД =Контрольные вопросы и задания1.Что называют ударом твердых тел? Две стадии удара. 2.Какой удар называют абсолютно упругим? Сформулируйте закон сохранения энергии и импульса для абсолютно упругого удара. 3.Какой удар называют абсолютно неупругим? Сформулируйте закон сохранения энергии и импульса для неупругого удара. 4.В какие виды энергии может превращаться механическая энергия при неупругом ударе тел? 5.Каков физический смысл коэффициента восстановления? От чего он зависит 6.Энергия остаточной деформации и ее физический смысл. Вывод формулы. Литература1.Лабораторный практикум по физике под ред. Ахматова А.С.-М.: Высшая школа, 1980. 2.Трофимова Т.И., Курс физики - М.: Высшая школа, 1985. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, град
град