СРО1. СРО1 Илюбаева Амина. Предмет и задачи динамики сооружений

• Название: Предмет и задачи динамики сооружений
• Дата: 11.11.2022
• Размер: 0.83 Mb.
• Имя файла: СРО1 Илюбаева Амина.docx
• Тип: Документы; #782791

Министерство Образования и Науки Республики Казахстан

НАО «Евразийский национальный университет им.Л.Н.Гумилева»

Архитектурно-строительный факультет

Кафедра «Строительство»

СРО №1

Дисциплина: Динамика и устойчивость сооружений

Тема: Предмет и задачи динамики сооружений

Проверил: Абильмаженов Т.Ш

Принял: Абильмаженов Т.Ш

Выполнил: Илюбаева А.

Группа: M124-7329-22-01

Астана

2022

План

1. Виды колебаний

2. Динамические воздействия, их особенности и классификация

3. Динамические расчетные схемы

4. Силы инерции

5. Литература

1. 
   Виды колебаний
   

При колебаниях происходит периодический переход одного вида энергии в другой, когда потенциальная энергия U (энергия, определяемая положением системы) переходит в ее кинетическую энергию K (энергию движения) и наоборот.

Если в консервативную систему внешняя энергия не поступает, то сумма ее потенциальной и кинетической энергий U+K остается постоянной. Колебания таких систем считаются незатухающими. Когда в систему поступает внешняя энергия, то ее колебания нарастают. Если же энергия системы уменьшается (например, из-за трения), колебания затухают.

Наглядное представление колебательного процесса можно получить, если построить график колебаний отдельной массы системы в координатах y-t (y − перемещение, t − время). На рис. 1 показаны соответствующие нарастающие, незатухающие и затухающие колебания.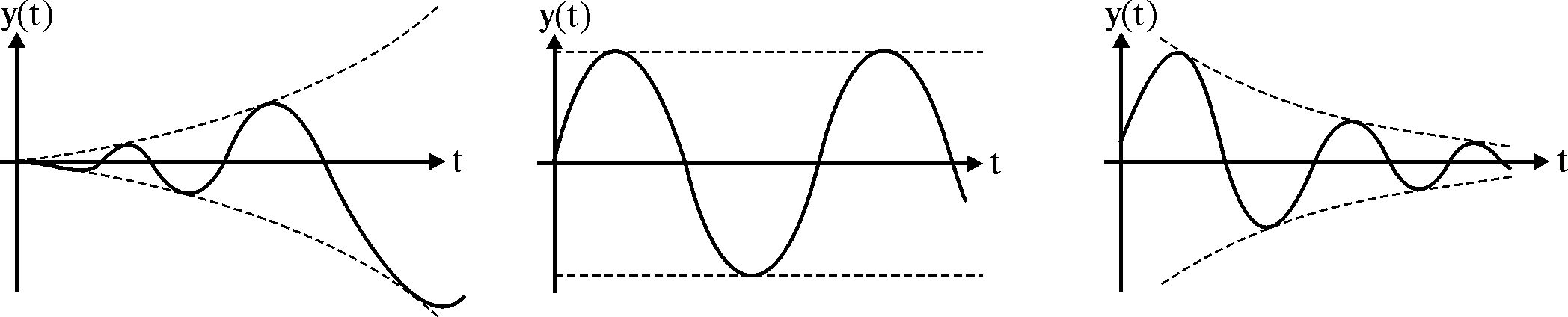




Рис. 1

Важной характеристикой колебательного процесса является форма колебаний. Форма колебаний определяется перемещениями точек колебательной системы в фиксированный момент времени относительно положения равновесия. Простейшие формы колебаний можно наблюдать. Например, можно видеть как качаются провода между столбами линии электропередач, струна музыкального инструмента, защемленная одним концом ученическая линейка и т.д. При построении формы колебаний, полученной расчетным путем, находят положение точек сооружения в фиксированный момент времени и соединяют их плавной кривой.

Если внешним воздействием нарушить равновесие колебательной системы, и затем прекратить это воздействие, она начнет совершать колебания относительно первоначального положения равновесия. Такие колебания называются свободными. Свободные колебания зависят от внутренних характеристик системы и от начальных условий (смещений, скоростей, ускорений) в момент снятия внешнего воздействия.

В реальных условиях свободные колебания затухают. Это связано с уменьшением энергии диссипативной системы за счет внешнего и внутреннего трения. Энергия консервативной системы не убывает, поэтому ее свободные колебания не должны затухать. Такие незатухающие колебания консервативной системы называются собственными колебаниями. Это название связано с тем, что формы и частоты собственных колебаний определяются только собственными характеристиками системы (распределением масс, жесткостей, геометрией, типом опор и т.д.). Т.к. консервативных систем в природе не существует, то и собственные колебания возможны только теоретически.

Большое практическое значение имеет изучение периодических колебаний, удовлетворяющих условию

y(t) y(t T), (1.4)

где T − период колебаний, т.е. время одного колебания.

Периодические колебания характеризуются круговой частотой, технической частотой и амплитудой колебаний. Круговая (циклическая) частота ω − это число колебаний за 2π секунды. Техническая частота f (или просто частота) − это число колебаний за одну секунду. Их можно определять по формулам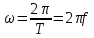

(измеряется в рад/с), (1.5)

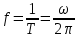(измеряется в Гц). (1.6)

Амплитуда колебаний − это половина общего размаха колебаний:

^a  ^{ymax– ymin} ^{/ 2.} (1.7)

Периодические колебания, которые совершаются по законам

y(t) asin(ωt ϕ )или y(t) acos(ωt ϕ ) (1.8)

называются гармоническими колебаниями. Величина в скобках называется фазой колебаний, а φ − начальной фазой колебаний.

Если колебательная система находится под воздействием переменных возмущающих сил, вызванные ими колебания называются вынужденными. Вынужденные колебания зависят от параметров колебательной системы и внешнего воздействия.

В технике широко используется термин вибрация. Он является синонимом термина “колебание” и используется в том случае, когда колебания имеют относительно малую амплитуду и не слишком низкую частоту.

2. 
   Динамические воздействия, их особенности и классификация
   

Для определения реакции систем при динамических нагрузках используются два принципиально разных подхода − детерминированный и недетерминированный подходы. Выбор одного из них зависит от способов воздействия и изменения нагрузки.

Когда изменение нагрузки во времени хорошо известно, ее называют детерминированнойнагрузкой. При такой нагрузке обычно можно установить изменение перемещений колебательной системы во времени в соответствии с изменением нагрузки. Другие параметры, такие как напряжения, деформации, внутренние усилия и др., могут быть определены на втором этапе расчета по результатам вычисления перемещений.

Если изменение нагрузки во времени известно не полностью, но может быть установлено с некоторой вероятностью, ее называют случайнойдинамическойнагрузкой. Случайная нагрузка может быть определена только статистически, а перемещения от нее могут быть описаны только как вероятные. Поэтому при недетерминированной нагрузке изменение перемещений во времени не вычисляют, а другие величины (напряжения, внутренние усилия и др.) определяют непосредственно из статического расчета.

В отличие от статических, динамические нагрузки изменяются во времени: по величине, направлению, положению. Они сообщают массам ускорения, вызывают появление инерционных сил и могут привести к сильным колебаниям сооружения, а в итоге − к их разрушению.

Рассмотрим основные виды детерминированных нагрузок. К ним относятся периодические, импульсные и подвижные нагрузки.

Периодическиенагрузки− это нагрузки, прикладываемые к сооружениям через определенный период. Источником возникновения периодических нагрузок являются различные машины и механизмы (электродвигатели, вентиляторы, центрифуги, грохоты, металлообрабатывающие станки, дробилки, насосы и др.). Если эти машины и механизмы жестко закреплены на сооружении и имеют неуравновешенные вращающиеся части, при их работе возникают гармонические нагрузки (нагрузки, изменяющиеся по закону синуса или косинуса). Их часто называют вибрационныминагрузками.

В качестве примера рассмотрим консольную балку с установленным на ней работающим двигателем (рис. 2 а).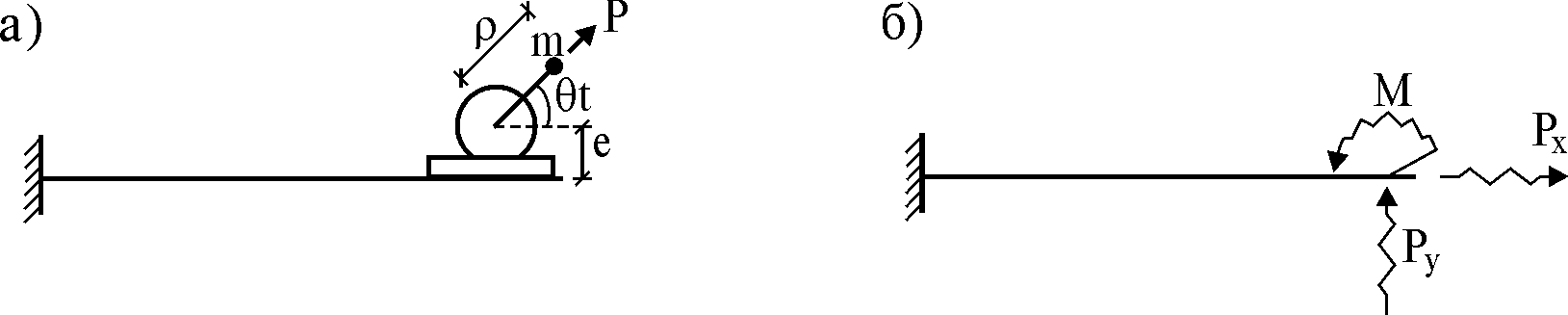




Рис. 2

Существует ряд машин и механизмов с возвратно-поступательным движением (поршневые компрессоры и насосы, дробилки, штамповочные машины), передающих на сооружение периодическую негармоническуюнагрузку. Такую нагрузку с помощью рядов Фурье можно разложить на сумму гармонических нагрузок. Например, нагрузку, изображенную на рис. 3 а,

Рис. 3

можно приближенно представить в виде суммы только трех членов ряда Фурье − трех гармонических нагрузок (рис. 3 б); при этом получаем форму нагрузки, близкую к исходной (рис. 3 в).

Импульсные нагрузки создаются взрывом, падающими грузами или частями силовых установок: молотов, копров и др. Они характеризуются кратковременным или мгновенным действием (рис. 4 а). Кратковременныеимпульсы(рис. 4 б) определяются величиной, формой и продолжительностью действия импульса. Мгновенныеимпульсы(рис. 4 в) определяются только величиной импульса.

Рис. 4

Подвижные нагрузки – это нагрузки, положение которых меняется с течением времени. Например, нагрузки от железнодорожного состава, автомобилей и др. являются подвижными нагрузками.

Динамические нагрузки могут быть и комбинированными. К примеру, таковой является ударно-вибрационная нагрузка от копра.

К недетерминированным нагрузкам относятся ветровые, взрывные и сейсмические нагрузки. У таких нагрузок какой-то один или несколько параметров (направление, время, интенсивность воздействия, частота и др.) являются неопределенными. Например, ветер характеризуется нерегулярным направлением и беспорядочным изменением скорости во времени. Интенсивность нагрузки, действующей при землетрясении, может быть не только чрезвычайно большой, но и весьма нерегулярной. На рис. 5 приведена акселограмма ускорений основания при сейсмической нагрузке.



Рис. 5

3. Динамические расчетные схемы

Под понятием расчетной динамической схемой понимается схема расположения совокупности инертных элементов системы, при расчетах на динамические воздействия.

Динамическая расчетная схема классифицируется в зависимости от числа степеней свободы, которое определяется положением инертных элементов в плоскости или пространстве в любой момент времени.

Сосредоточенная масса имеет в плоскости 2 степени свободы, а в пространстве 3 степени свободы.

Тело определенных размеров в плоскости имеет 3 степени свободы, а в пространстве 6.

По числу степени свободы расчетная схема динамического сооружения классифицируется на:

1. Системы с 1 степенью свободы

2. Системы с конечным числом степени свободы

3. Системы с бесконечным числом степени свободы

4. Силы инерции

Сила инерции (также инерционная сила) — многозначное понятие, применяемое в механике по отношению к трём различным физическим величинам. Одна из них — «даламберова сила инерции» — вводится в инерциальных системах отсчёта для получения формальной возможности записи уравнений динамики в виде более простых уравнений статики. Другая — «эйлерова сила инерции» — используется при рассмотрении движения тел в неинерциальных системах отсчёта. Наконец, третья — «ньютонова сила инерции» — сила противодействия, рассматриваемая в связи с третьим законом Ньютона.

Общим для всех трёх величин является их векторный характер и размерность силы. Кроме того, первые две величины объединяет возможность их использования в уравнениях движения, по форме совпадающих с уравнением второго закона Ньютона, а также их пропорциональность массе тел.

5.Литература

1. 
   Сила инерции / Самсонов В. А. // Большая российская энциклопедия : [в 35 т.]/ гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
   
2. 
   Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—15. — 320 с.
   
3. 
   Динамика и устойчивость сооружений, Р.А. Шакирзянов, Ф.Р. Шакирзянов., Казань, Ай Пи Ар Медиа, 2022, 119 с;
   
4. 
   Динамика и устойчивость сооруже-ний, А. М. Масленников, Москва, Издательство Юрайт, 2017, 366 с;