|
|
рабочая прграмма. Лекция по теме Взаимное расположение прямых в пространстве. (Урок геометрии в 10 классе) Цель урока изучить вопрос о взаимном расположении двух прямых а пространстве
Урок-лекция по теме
«Взаимное расположение прямых в пространстве».
(Урок геометрии в 10 классе)
Цель урока: изучить вопрос о взаимном расположении двух прямых а пространстве.
Задачи:
- повторить некоторые положения планиметрии;
- сформулировать первые определения школьного курса стереометрии;
- доказать теорему о параллельных прямых в пространстве, проследить связь с аналогичными утверждениями планиметрии;
- продолжить формирование навыка выполнения пространственных чертежей;
- способствовать развитию пространственного воображения учащихся.
ПЛАН ЛЕКЦИИ
Лекция № 2. Взаимное расположение прямых в пространстве.
Определение параллельных прямых в пространстве.
Скрещивающиеся прямые.
Теорема о параллельных прямых.
Транзитивность параллельности прямых в пространстве (самостоятельно)
Признак скрещивающихся прямых.
ОБОРУДОВАНИЕ
Компьютер, проектор, экран, доска.
Программное обеспечение: УМК «Живая математика»
ТЕХНОЛОГИЯ
Лекционно-семинарская система обучения (форма: лекция с остановками) с элементами проблемного обучения
Некоторые замечания.
1) На данном уроке будут рассмотрены п.п. 1 – 4 лекции № 2
2) Планы лекций учащимся выданы заранее.
3) Дома уч-ся должны повторить определения пересекающихся и параллельных прямых на плоскости, теорему о прямой, проходящей в плоскости через данную точку параллельно данной прямой, аксиому параллельных прямых
4) Необходимые чертежи будут представлены в демонстрационных моделях.
НО учитель обязательно дублирует их на доске для того, чтобы дать учащимся возможность проследить, как выполняются пространственные чертежи «руками».
Приложение 1.
Демонстрационные модели
Модель 1
Модель 2 (исходное положение) Модель 2 (конечное положение)
Модель 3 Модель 4
 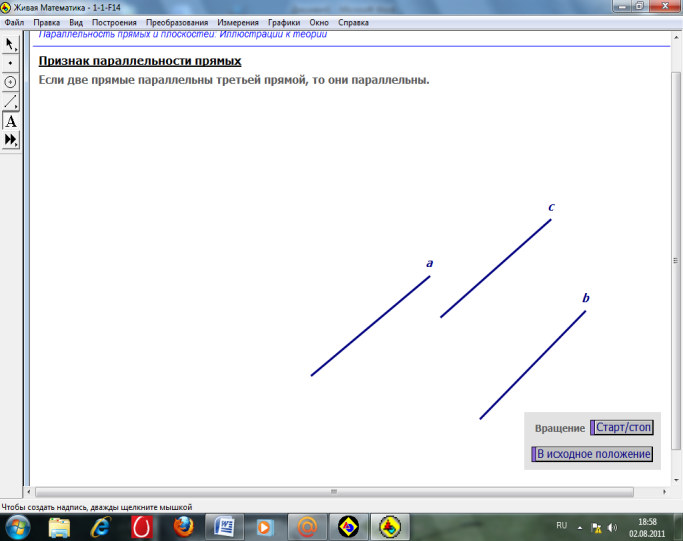
Модель 5
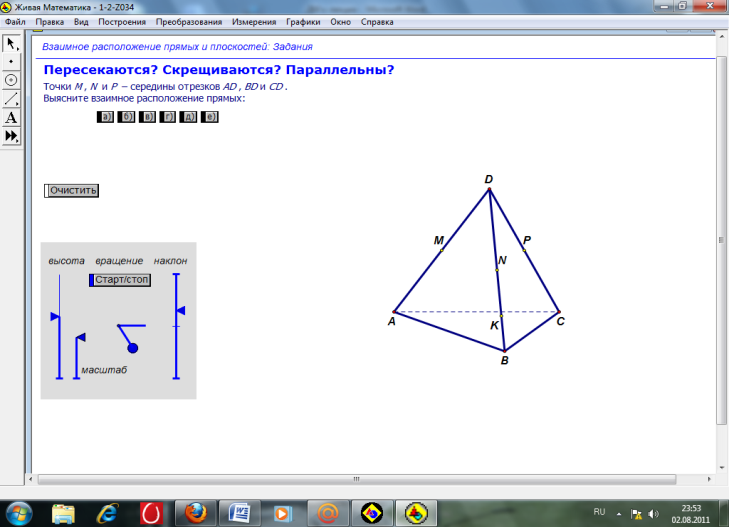
ХОД УРОКА
Содержание урока
|
Текст лекции
|
Примечания.
Номер дем.модели
|
I. Введение в лекцию
1) Повторение теоретического материала: аксиомы и следствия к ним.
2) Задание 1. Продемонстрировать на моделях возможные случаи взаимного расположения прямых на плоскости.
3) Задание 2. Смоделировать возможные случаи взаимного расположения прямых в пространстве.
Проблема. Описать возможные случаи взаимного расположения прямых в пространстве, сформулировать соответствующие определения.
(учащиеся сами пытаются сформулировать определения. Затем учитель диктует строгие определения, делает чертежи, вводит обозначения )
II. Лекция № 2, п.1 - 2
1) Уч-ся записывают текст п.п.1- 2
2) Демонстрация Опр.1 и Опр.2 на компьютерной модели
3) Демонстрация Опр.3 на компьютерной модели
4) Учащиеся вслед за учителем зарисовывают в тетрадях схему «Взаимное расположение двух прямых в пространстве»
|
Лекция № 2. Взаимное расположение прямых в пространстве.
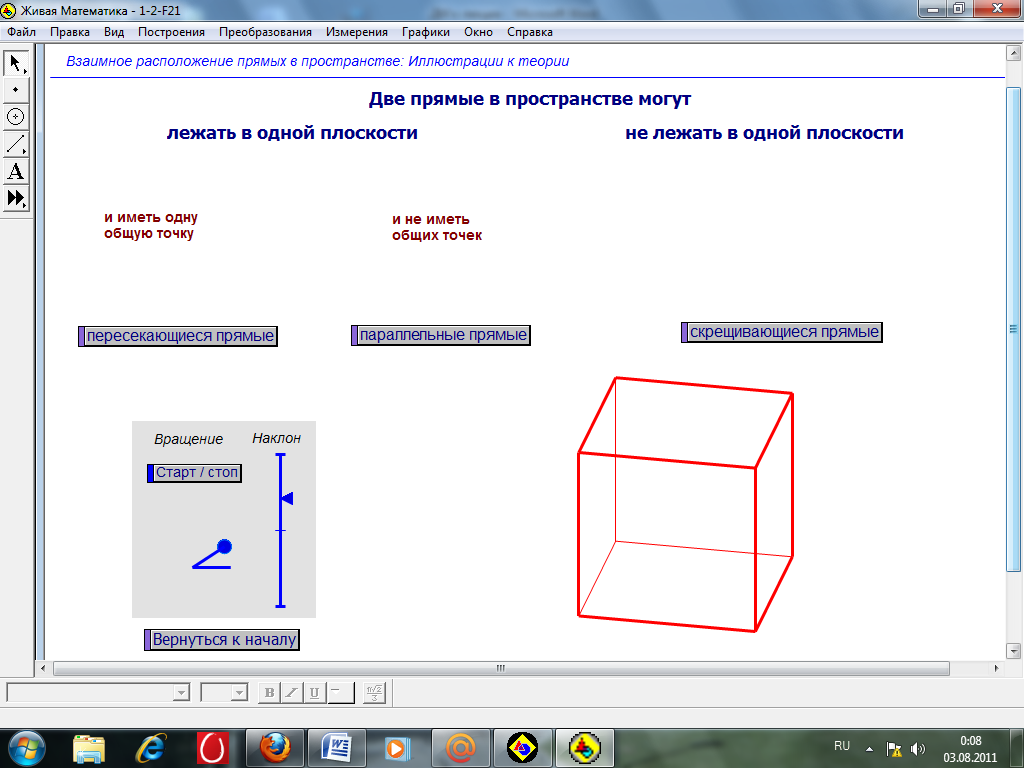
п.1. Определение 1. Две прямые в пространстве называются пересекающимися, если они имеют общую точку. (рисунок)
Определение 2. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. (рисунок, обозначение)
п.2. Определение 3. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. (рисунок, обозначение)
Взаимное расположение двух прямых в пространстве
Две прямые
 Лежат Не лежат Лежат Не лежат
в одной плоскости в одной плоскости
имеют одну не имеют
общую общих
точку точек
пересекаются параллельны являются скрещивающимися
|
Д.М. № 1
|
III. Лекция № 2, п.3
1) Задание 1. Сформулировать теорему о прямой, проходящей в плоскости через данную точку параллельно данной прямой и аксиому параллельных прямых.
2) Проблема. Является ли утверждение, аналогичное аксиоме, аксиомой в пространстве? (Нет)
При обсуждении данной проблемы можно использовать начальное положение Д.М. №2.
3) Сформулировав теорему, учитель обращает внимание уч-ся на особенность ее структуры :это теорема «существования и единственности».
Доказательство проводится в форме эвристической беседы.
|
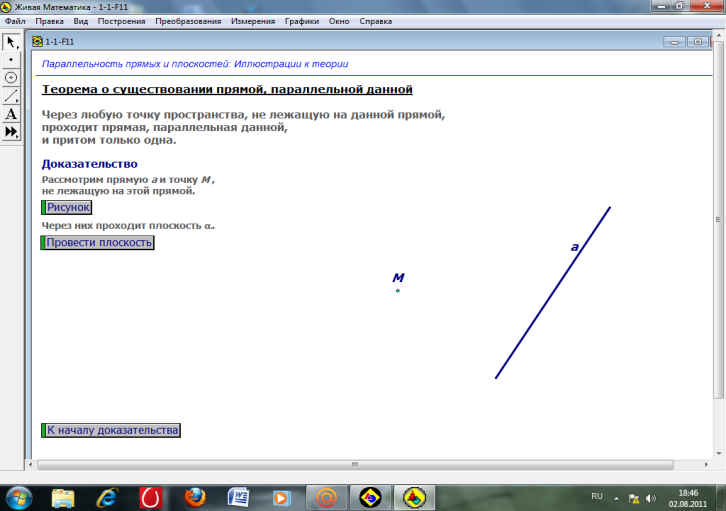
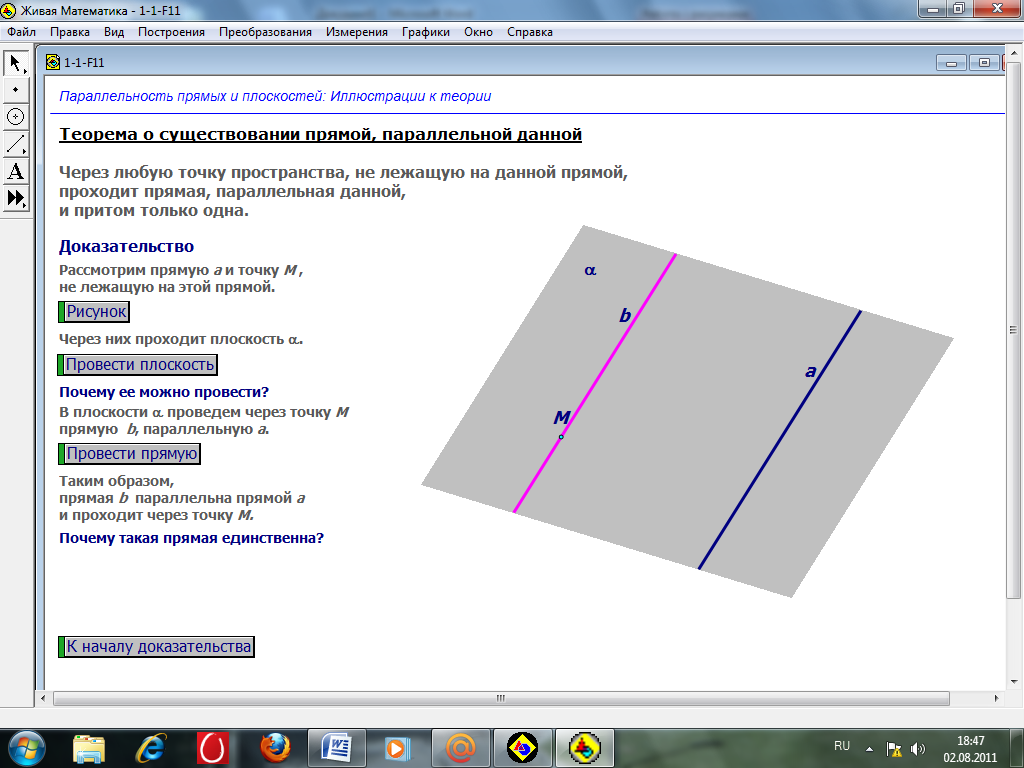
п.3.
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна
Доказательство.
I. Существование.
II. Единственность.
|
Д.М. № 2
Доказательство проводится в соответствии с планом, содержащимся в модели.
|
IV. Лекция № 2, п.4.
1) Учитель формулирует название теоремы.
Задание. По названию теоремы дать ее точную формулировку. (Предполагается, что уч-ся знакомы со свойством транзитивности)
2) Учитель обращает внимвние уч-ся на то, что для доказательства теоремы потребуется вспомогательная теорема – лемма; затем сам формулирует и доказывает лемму. Учащиеся записывают только ее формулировку, краткое условие и рисунок
3) Доказательство теоремы уч-ся самостоятельно разбирают дома по учебнику, записывают в тетрадь по пунктам.
V. Постановка Д.З.
1) Выучить теорию.
2) Разобрать и записать доказательство теоремы п.4.
3) Повторить материал лекции № 1.
VI. Подведение итогов урока. Контроль понимания.
Задание 1. Рассказать о всех возможных случаях взаимного расположения двух прямых в пространстве.
Задание 2. Определить взаимное расположений прямых
|
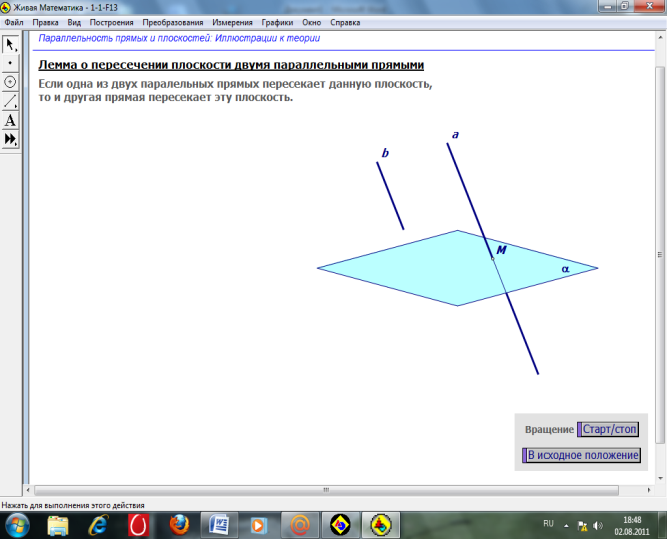
п.4
Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Дано:
Доказать:
(рисунок)
Теорема о транзитивности параллельности прямых в пространстве.
Если две прямые параллельны третьей, то они параллельны.
|
Д.М.№ 4
Д.М. № 3. Доказательство проводится с помощью модели
Д.М. № 5,
Задания а) – г)
| |
|
|
 Скачать 0.7 Mb.
Скачать 0.7 Mb.






 Лежат Не лежат
Лежат Не лежат