Расположения прямой и плоскости в пространстве. Случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице
 Скачать 154.28 Kb.
|
|
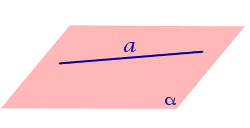
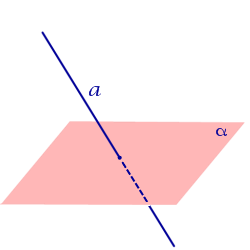
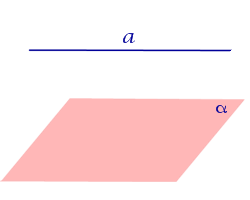
Случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице.
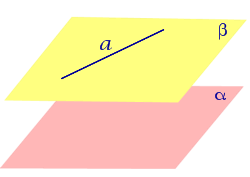
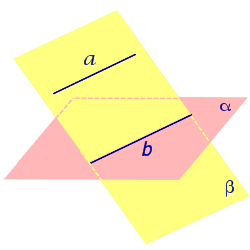
Утверждение 1. Предположим, что прямая a и плоскость α параллельны, а плоскость β проходит через прямую a. Тогда возможны два случая: Плоскость β параллельна плоскости α (рис.1); Плоскость β пересекает плоскость α. В этом случае прямая b, которая является линией пересечения плоскостей α и β , будет параллельна прямой a (рис.2).
Доказательство. Рассмотрим случай 2 и предположим противное. Предположим, что прямые a и b пересекаются в некоторой точке P (рис.3) 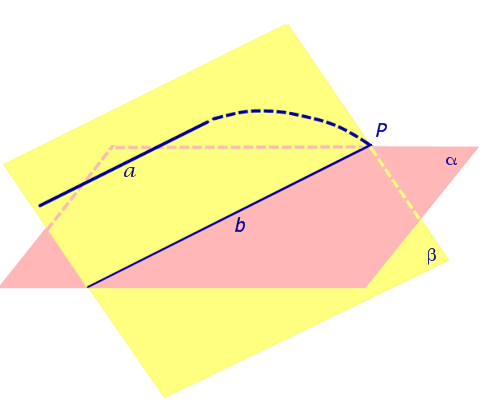 Рис.3 Но тогда точка P оказывается точкой пересечения прямой a и плоскости α, и мы получаем противоречие с тем, что прямая a и плоскость α параллельны. Полученное противоречие и завершает доказательство утверждения 1. Утверждение 2 (признак параллельности прямой и плоскости). Если прямая a, не лежащая в плоскости α, параллельна некоторой прямой b, лежащей в плоскости α, то прямая a и плоскость α параллельны. Доказательство. Докажем признак параллельности прямой и плоскости "от противного". Предположим, что прямая a пересекает плоскость α в некоторой точке P. Проведем плоскость β через параллельные прямые a и b (рис. 4). Рис.4 Точка P лежит на прямой a и принадлежит плоскости β. Но по предположению точка P принадлежит и плоскости α , следовательно точка P лежит на прямой b , по которой пересекаются плоскости α и β . Однако прямые a и b параллельны по условию и не могут иметь общих точек. Полученное противоречие завершает доказательство признака параллельности прямой и плоскости. Углом между прямой и плоскостью Углом между прямой и плоскостью называют угол между прямой и ее проекцией на эту плоскость. Чтобы построить проекцию прямой на плоскость, достаточно опустить из любых двух ее точек перпендикуляры на плоскость (спроектировать эти точки), после чего провести через них прямую – это и будет проекция (см. Рис. 5). 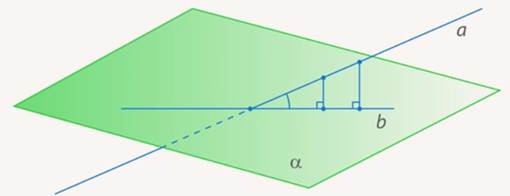 Рис. 5. Угол между прямой и плоскостью Так, проекции всех точек данной прямой будут лежать на одной прямой. Доказательство Пусть 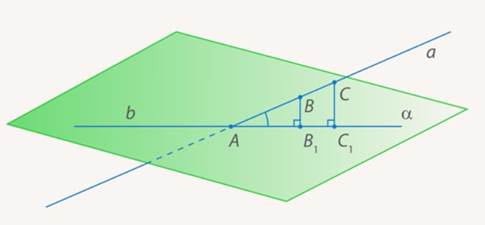 – точка пересечения прямой  и плоскости  ,  и  – точки на прямой ,  и  – их проекции на плоскость . Докажем, что , и лежат на одной прямой  . (См. Рис. 6.) Рис. 6. Иллюстрация к доказательству Заметим, что 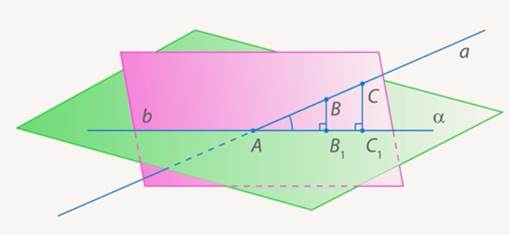 , так как  ,  . Значит если рассмотреть плоскость  , то точки и будут принадлежать ей. Но плоскость пересекает исходную плоскость по некоторой прямой. (См. Рис. 7.) Рис. 7. Пересечение плоскостей Значит раз точки , и принадлежат обеим плоскостям, то они лежат на этой прямой, что и требовалось доказать.То есть мы свели новое определение к углу между прямыми, который мы уже знаем. Обратите внимание на частую ошибку, которую допускают ученики. Углом между прямой и плоскостью называется угол именно между прямой и ее проекцией, а не между прямой и любой прямой в плоскости. Потому как такие углы могут быть разными. В пространстве   .l 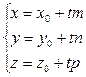 Возможны следующие случаи взаимного расположения прямой  и плоскости в пространстве:1. Прямая пересекается с плоскостью , т.е. имеет с ней единственную общую точку.Am+Bn+Cp≠0. 2. Прямая параллельна плоскости , но не лежит в этой плоскости, т.е. общих точек они не имеют.Am+Bn+Cp=0, Ax0+By0+Cz0+D≠0. 3. Прямая лежит в плоскости .Am+Bn+Cp=0, Ax0+By0+Cz0+D=0. Углом между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость. .l 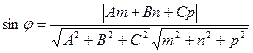  Угол между прямой и плоскостью. Пусть дана прямая, заданная каноническими уравнениями 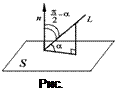 (1)и плоскость  . (2) Углом между прямой  и плоскостью  считают острый угол  между этой прямой и ее проекцией на плоскость (рис.1).Этот угол определяется равенством  .192. Взаимное расположение прямой и плоскости. Прямая (1) параллельна плоскости (2) тогда и только тогда, когда направляющий вектор этой прямой  перпендикулярен нормальному вектору  данной плоскости.Отсюда получаем условие параллельности прямой (1) и плоскости (2):  .Прямая (1) перпендикулярна плоскости (2) в том и только том случае, когда направляющий вектор этой прямой коллинеарен нормальному вектору плоскости, что равносильно следующему равенству: .Найдем теперь условия, при которых прямая (1) принадлежит плоскости (2). Это будет тогда и только тогда, когда одновременно будут выполняться два равенства:  (3)где первое из равенств (3) означает, что точка 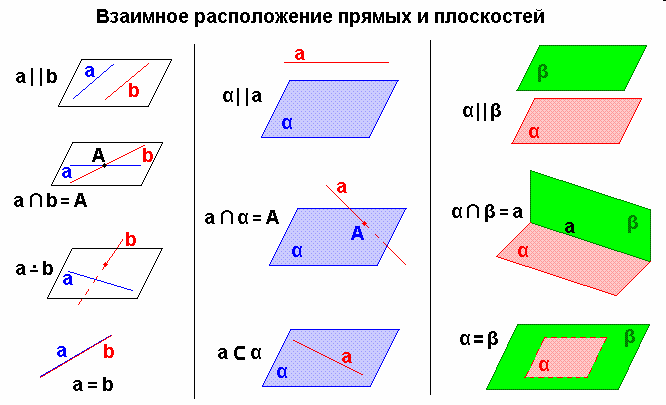 , через которую проходит прямая (1), принадлежит плоскости (2), а второе равенство из (3) выражает условие параллельности прямой (1) и плоскости (2). Теоремы • Если прямая, пересекающая плоскость, перпендикулярна двум прямым, лежащим в этой плоскости и проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости. • Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. • Если две прямые перпендикулярны одной и той же плоскости, то они параллельны. • Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. • Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, расположенной в этой плоскости, то она параллельна этой плоскости. • Если прямая параллельна плоскости, то она параллельна некоторой прямой на этой плоскости. • Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны. • Все точки прямой, параллельной плоскости, одинаково удалены от этой плоскости.  |
