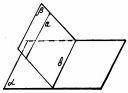
8. Признак параллельности прямой и плоскости Если прямая, не лежащая в данной плоскости, параллельна какойнибудь прямой
 Скачать 2 Mb. Скачать 2 Mb.
|
|
8. Признак параллельности прямой и плоскости: Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости Замечания.
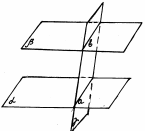
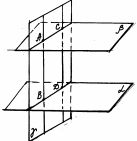
Параллельность двух плоскостей Определение. Две плоскости называются параллельными, если они не имеют общих точек. Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Свойства параллельных плоскостей:
15.Точка и линия на поверхности. В общем случае линия может принадлежать поверхности или не принадлежать. Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности. Исключение составляет случай, когда линия представлена прямой, а поверхность — плоскостью. В этом случае для принадлежности прямой плоскости достаточно, чтобы хотя бы две точки ее принадлежали этой поверхности. Точка может принадлежать поверхности и не принадлежать. Точка принадлежит поверхности, если она лежит на линии, расположенной на этой поверхности. 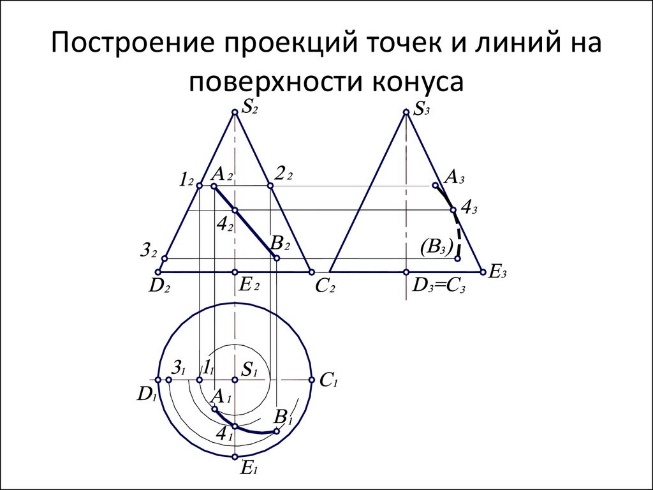 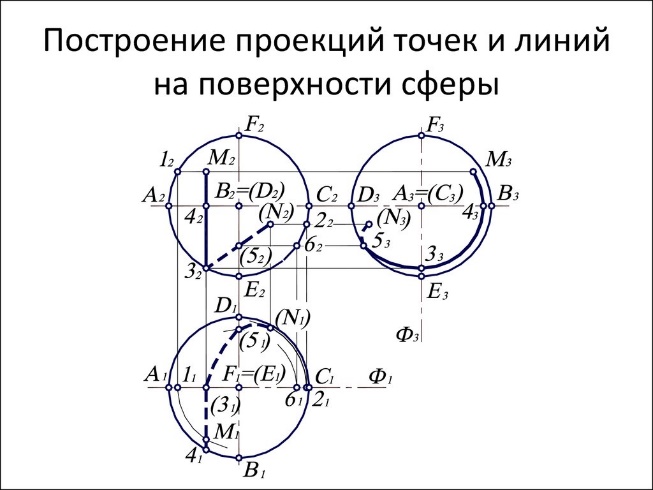 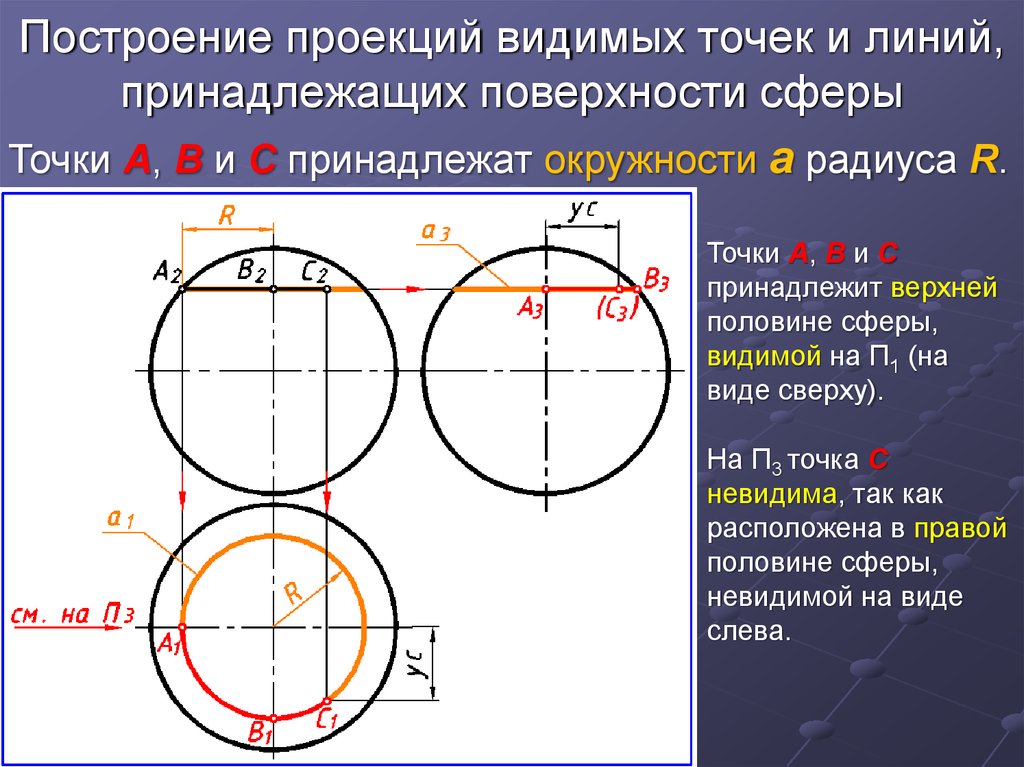 16.Сечение поверхностей плоскостью А) Сечение пирамиды плоскостью, развертка усеченной части 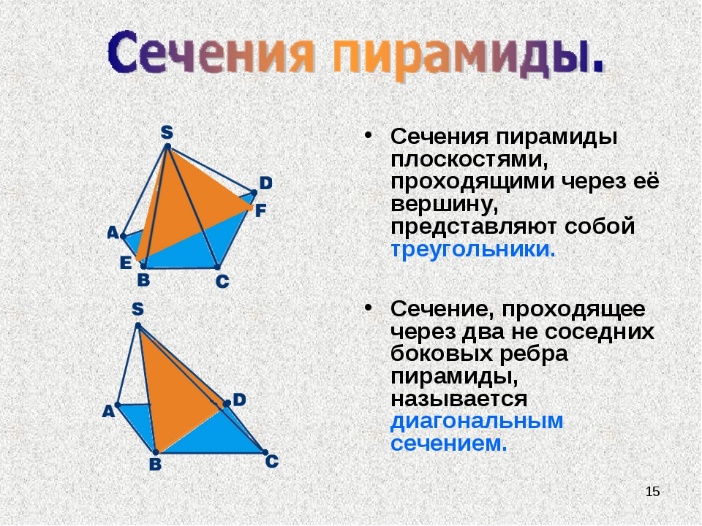 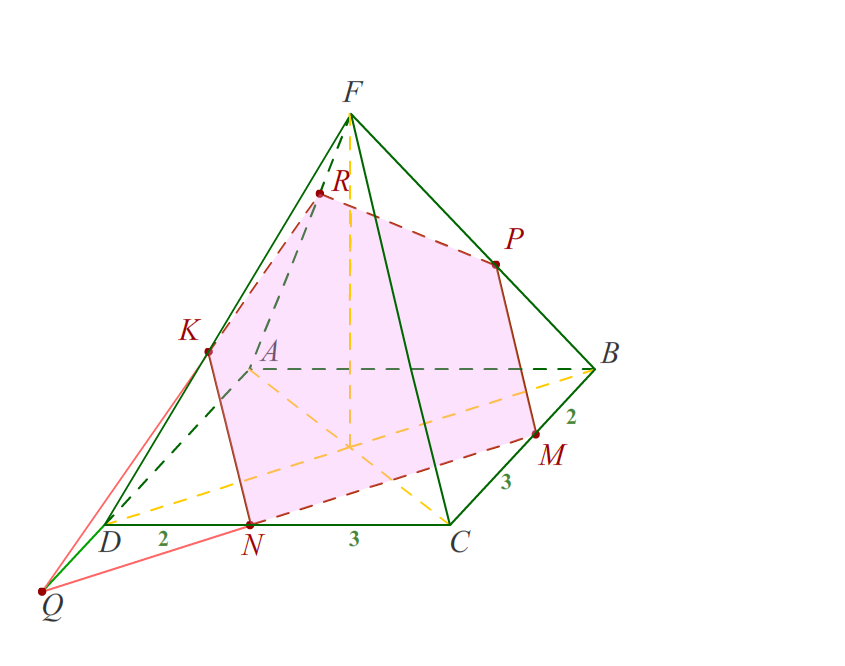 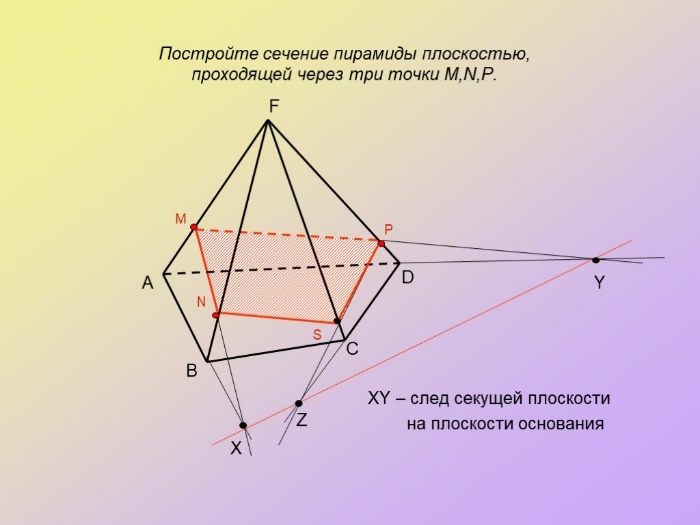 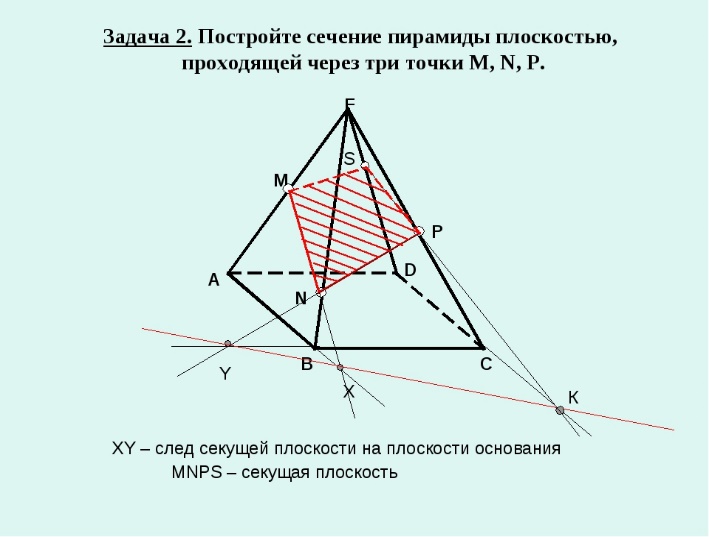  Б) Сечение прямой и наклонной призмы плоскостью, развертка этих частей 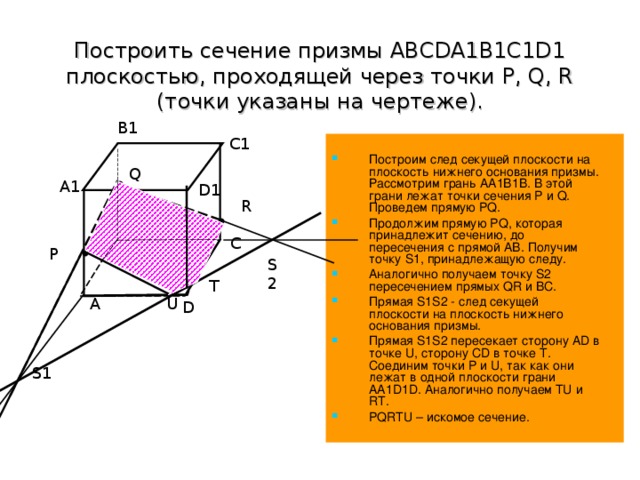 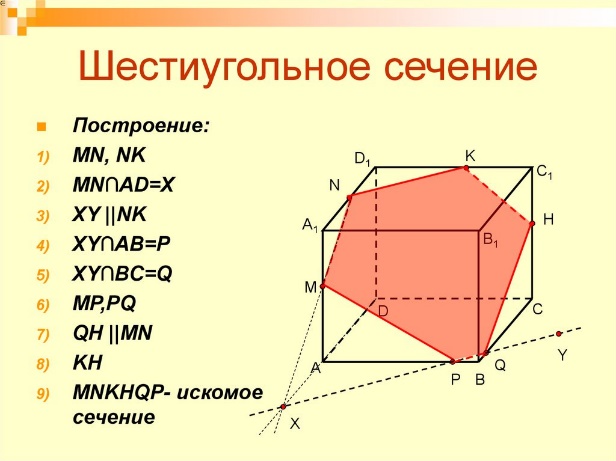  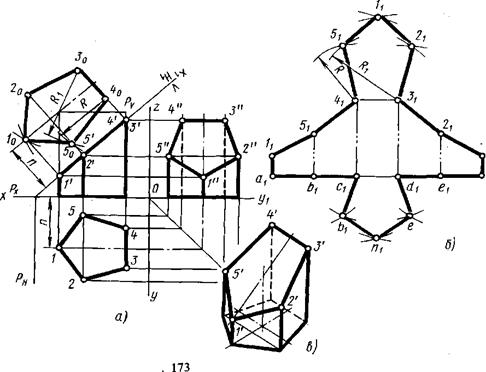  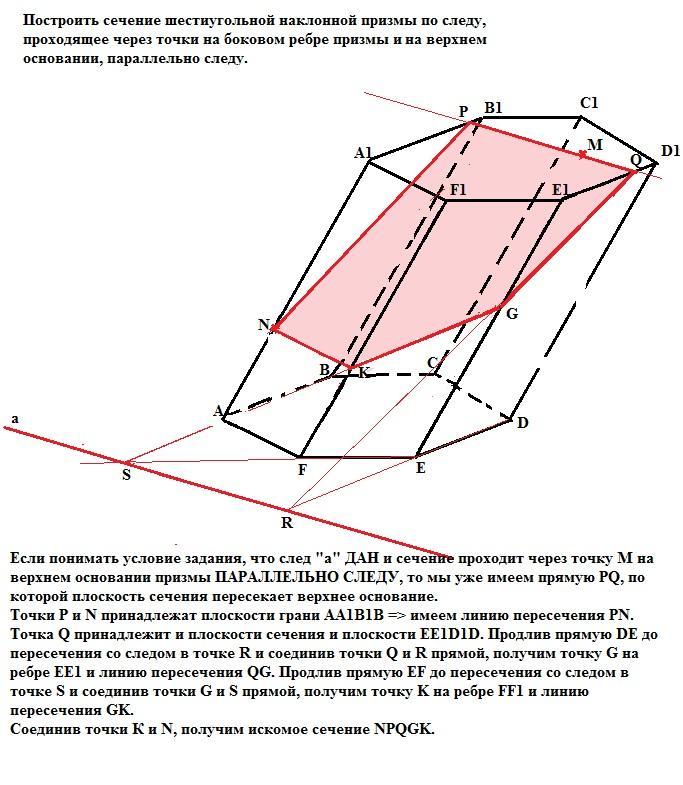 В) Сечение цилиндрических поверхностей, развертка этих поверхностей 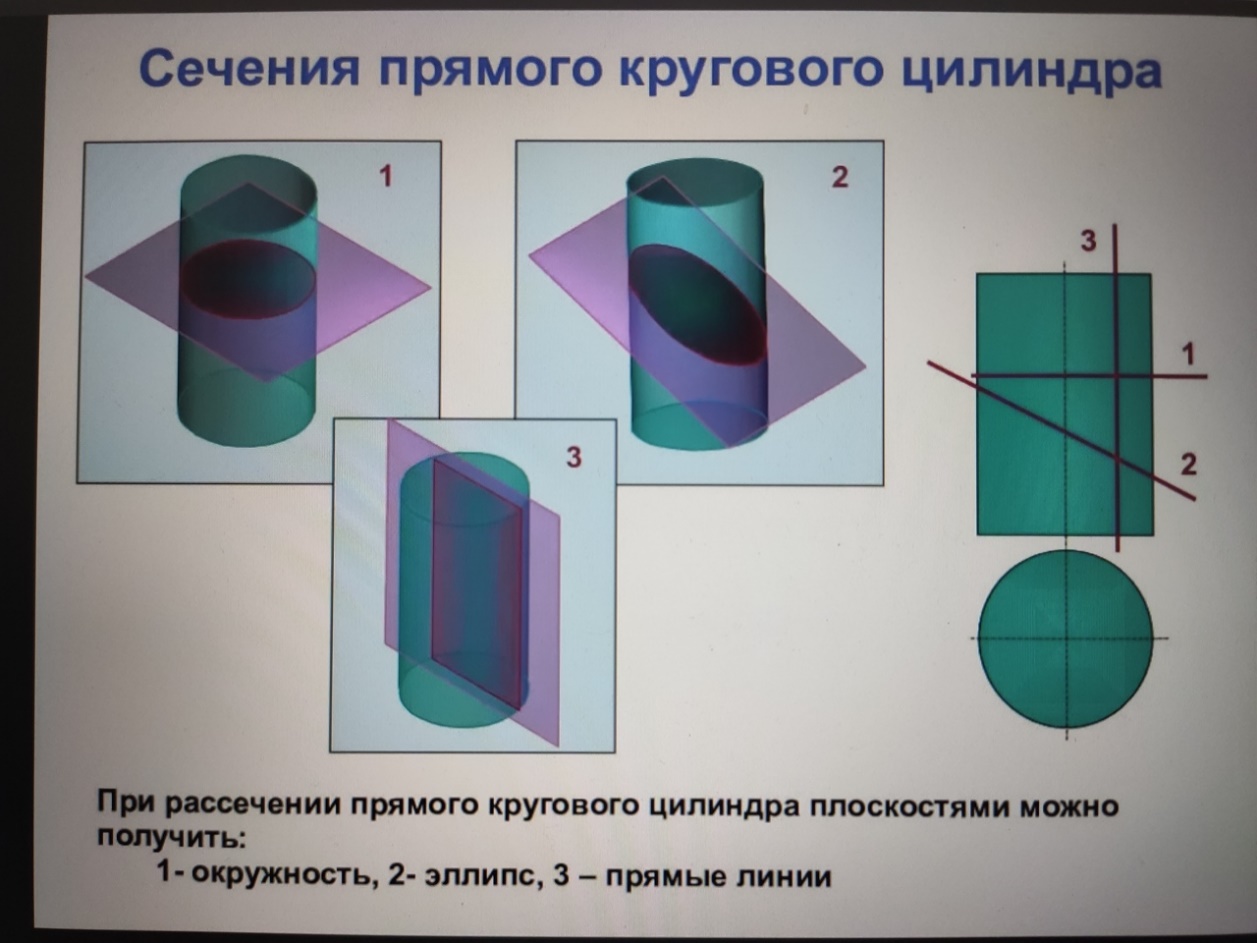 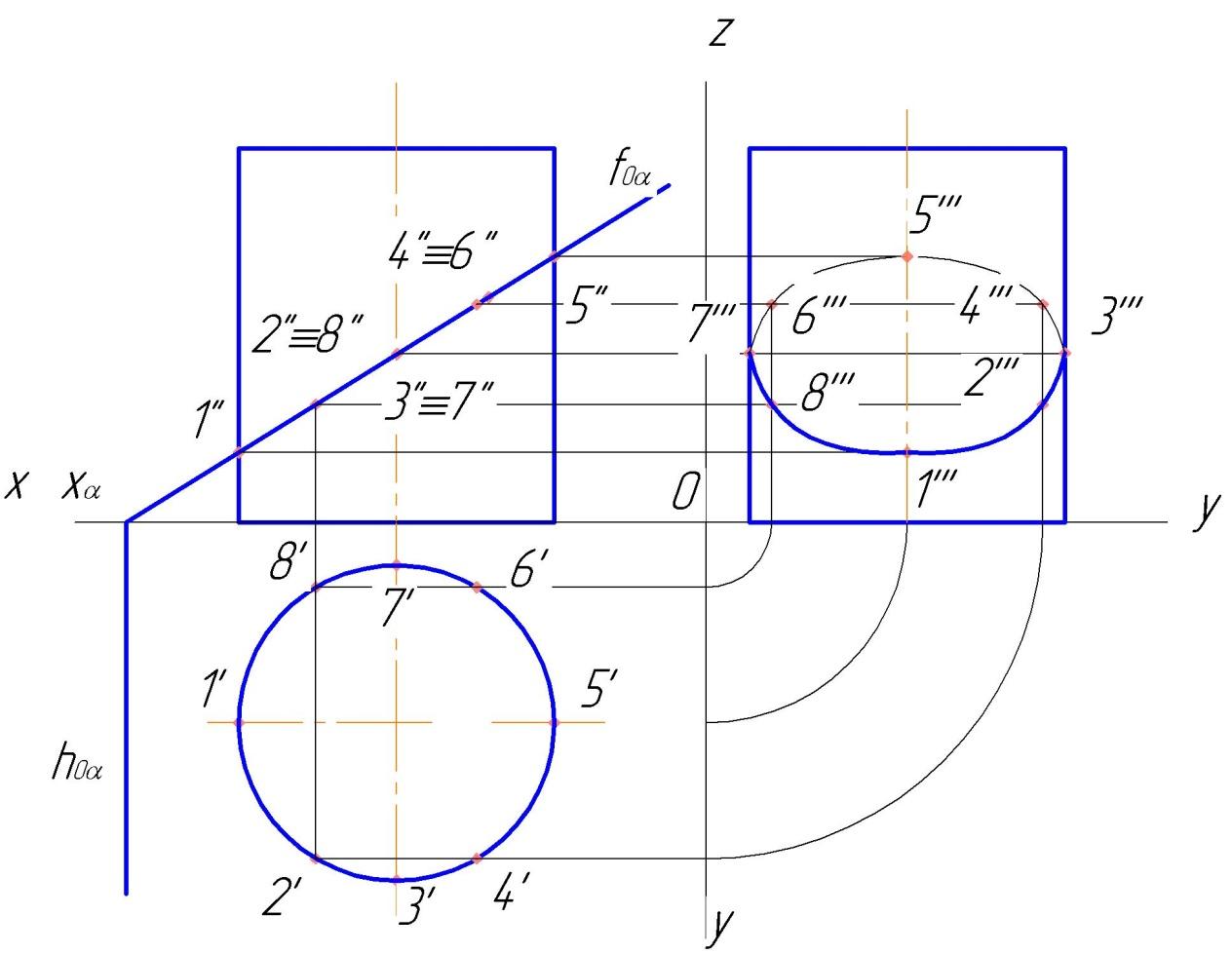 Г) Сечение прямого конуса плоскостью, развертка поверхности   |