Лекция_6_Прямая_на_плоскости_Плоскость-1. Лекция Прямая на плоскости
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
1 2 6. Найдем отклонение и расстояние от точки 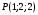 до плоскости до плоскости  . Для этого подставим координаты точки Pв нормальное уравнение плоскости и найдем отклонение: . Для этого подставим координаты точки Pв нормальное уравнение плоскости и найдем отклонение: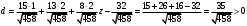 . .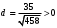 - точка - точка 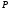 и начало координат лежат по разные стороны от плоскости и начало координат лежат по разные стороны от плоскости  . .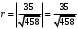 - расстояние от точки - расстояние от точки 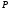 до плоскости до плоскости  . .Пример 2. Даны три плоскости, заданные своими общими уравнениями. Определить имеют ли они единственную точку пересечения, если имеют то найти ее. Сделать проверку. Найти угол между плоскостями 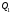 и и 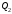 . .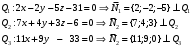 . .1. Составим и найдем значение определителя 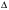 из координат нормальных векторов плоскостей: из координат нормальных векторов плоскостей: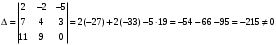 . .Определитель 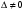 , следовательно, плоскости имеют единственную точку пересечения. Решим систему, составленную из общих уравнений плоскостей методом Гаусса: , следовательно, плоскости имеют единственную точку пересечения. Решим систему, составленную из общих уравнений плоскостей методом Гаусса: 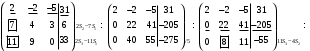 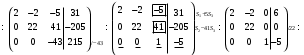 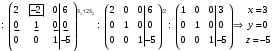 . .Точка пересечения плоскостей имеет координаты: 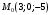 . Так как точка пересечения принадлежит всем трем плоскостям, то при ее подстановке во все три уравнения должны получиться тождества. Проверка: . Так как точка пересечения принадлежит всем трем плоскостям, то при ее подстановке во все три уравнения должны получиться тождества. Проверка: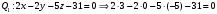 Верно. Верно.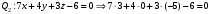 Верно. Верно.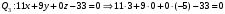 Верно. Верно.Точка пересечения найдена правильно. 2. Найдем угол плоскостями 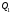 и и 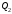 по формуле (17). по формуле (17).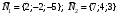 . .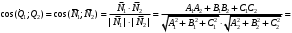 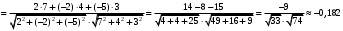 Тогда: 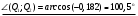 . .Пример 3. Проверить параллельность плоскостей 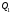 и и 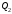 . Если плоскости параллельны, то найти расстояние между ними. . Если плоскости параллельны, то найти расстояние между ними.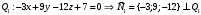 . .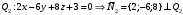 . .Проверим коллинеарность векторов 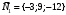 и и 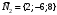 : :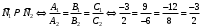 . .Координаты нормальных векторов пропорциональны, следовательно, плоскости 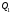 и и 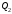 параллельны. параллельны.Положим в уравнении плоскости 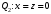 . Тогда . Тогда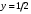 и точка и точка 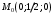 принадлежит принадлежит 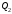 . .Найдем расстояние от точки 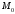 до плоскости до плоскости 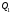 . Это и будет расстояние между параллельными плоскостями: . Это и будет расстояние между параллельными плоскостями: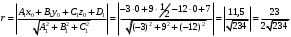 . .Таким образом, расстояние между параллельными плоскостями 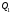 и и 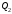 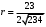 . .6.3. Задание №11 на практические занятия и самостоятельную работу. Решить самостоятельно: Задание 1. Записать девять уравнений прямой  , если точка , если точка 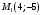 принадлежит прямой, а вектор принадлежит прямой, а вектор 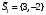 ей параллелен. ей параллелен.Задание 2. Даны две точки, принадлежащие прямой  : : 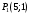 и и 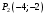 . Найти отклонение и расстояние от точки . Найти отклонение и расстояние от точки 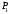 до прямой до прямой  из Примера 1. Если прямые из Примера 1. Если прямые  и и  не параллельны, то найти их точку пересечения. не параллельны, то найти их точку пересечения.Задание 3. Решить следующие задания из задачника А.В.Ефимов, Б.П.Демидович «Сборник задач по математике», часть 1 «Линейная алгебра и основы математического анализа»: Написать уравнение прямой, привести его к общему виду и построить прямую. Привести общее уравнение к нормальному виду и указать расстояние от прямой до начала координат: №2.142а._;_.'>2.142а. 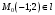 ; ;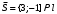 . №2.143а. . №2.143а.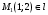 ; ; 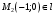 . .Исследовать взаимное расположение заданных прямых. Если они параллельны, то найти расстояние между ними, а если нет, то точку их пересечения и угол между ними: №2.145.  : :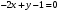 ; ;  : :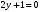 . №2.148. . №2.148. : :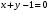 ; ;  : : 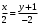 . .№2.150а. Треугольник 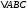 задан координатами вершин: задан координатами вершин: 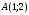 ; ; 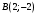 ; ; 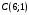 . Требуется: . Требуется:1.Написать уравнение стороны 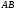 ; ;2.Написать уравнение высоты 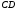 и найти ее длину и найти ее длину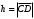 ; ;3.Найти угол 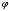 между высотой между высотой 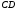 и медианой и медианой 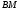 ; ;4.Написать уравнения биссектрис  и и  внутреннего и внешнего углов при вершине внутреннего и внешнего углов при вершине 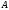 . При решении учесть, что биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. . При решении учесть, что биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон.№2.151. Показать, что точка 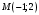 принадлежит прямой принадлежит прямой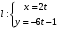 . Найти соответствующее этой точке значение параметра . Найти соответствующее этой точке значение параметра 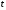 . .№2.153. Написать уравнение прямой, проходящей через точку 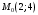 и отстоящей от точки и отстоящей от точки 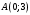 на расстояние на расстояние 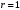 . .Ответы: №2.142а. 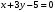 ; ;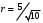 . №2.143а. . №2.143а. 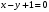 ; ; 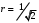 . .№2.145. Точка пересечения 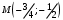 ; ; 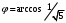 . №2.148.Параллельны, . №2.148.Параллельны, 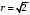 . .№2.150а. 1. 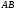 : : 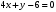 ; 2. ; 2.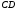 : : 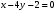 , ,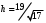 ; 3. ; 3. 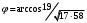 ; ;4. 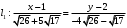 ; ; 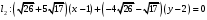 . .№2.151. 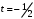 . №2.153. . №2.153.  : :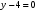 ; ;  : :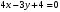 . .Решить дома: Задание 1. Записать девять уравнений прямой  , если точка , если точка 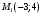 принадлежит прямой, а ее угловой коэффициент принадлежит прямой, а ее угловой коэффициент 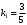 . .Задание 2. Даны две точки, принадлежащие прямой  : : 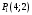 и и 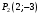 . Найти отклонение и расстояние от точки . Найти отклонение и расстояние от точки 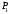 до прямой до прямой  из Примера 1. Если прямые из Примера 1. Если прямые  и и  не параллельны, то найти их точку пересечения и угол между прямыми не параллельны, то найти их точку пересечения и угол между прямыми  и и  . .Задание 3. 3.1. Проверить параллельность прямых: 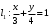 и и 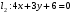 . Если они параллельны, то найти расстояние между ними, а если нет, то очку их пересечения. . Если они параллельны, то найти расстояние между ними, а если нет, то очку их пересечения. 3.2. Прямая  проходит через точку проходит через точку 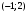 перпендикулярно прямой перпендикулярно прямой 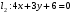 . Найти общее уравнение прямой . Найти общее уравнение прямой  . .3.3. Прямая  проходит через точки проходит через точки 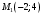 и и 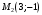 . Найти ее угловой коэффициент . Найти ее угловой коэффициент 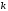 и записать ее общее уравнение. и записать ее общее уравнение.3.4. Угол наклона прямой  с положительным направлением оси с положительным направлением оси 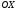 составляет составляет 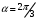 . Прямая . Прямая  проходит через точку проходит через точку 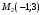 . Записать общее уравнение прямой . Записать общее уравнение прямой  . .3.5. Найти отклонение и расстояние от точки 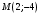 до прямой до прямой 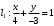 . На что указывает знак отклонения? . На что указывает знак отклонения?3.6. Дано общее уравнение прямой 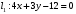 . Записать каноническое уравнение прямой. . Записать каноническое уравнение прямой.3.7. Прямые заданы уравнениями: 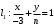 и и 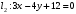 . При каком значении . При каком значении  эти прямые будут перпендикулярны. эти прямые будут перпендикулярны.3.8. Прямая  перпендикулярна к прямой перпендикулярна к прямой 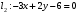 и отсекает по оси и отсекает по оси 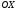 отрезок отрезок 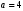 . Записать общее уравнение прямой . Записать общее уравнение прямой  . .3.9. Проверить параллельность прямых: 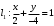 и и 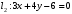 . Если они параллельны, то найти расстояние между ними, а если нет, то очку их пересечения. . Если они параллельны, то найти расстояние между ними, а если нет, то очку их пересечения. 3.10. Дано каноническое уравнение прямой 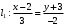 . Записать общее уравнение прямой . Записать общее уравнение прямой  . .3.11. Отрезок, отсекаемый прямой по оси 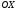 , равен , равен 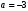 , угол, который прямая составляет с положительным направлением этой оси равен , угол, который прямая составляет с положительным направлением этой оси равен 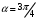 . Записать общее уравнение этой прямой. . Записать общее уравнение этой прямой.3.12. Прямая задана уравнением. 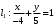 . Записать каноническое уравнение этой прямой и найти ее угловой коэффициент. . Записать каноническое уравнение этой прямой и найти ее угловой коэффициент.3.13. Дано каноническое уравнение прямой 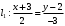 . Прямая . Прямая  перпендикулярна прямой перпендикулярна прямой  и проходит через точку, указанную в уравнении и проходит через точку, указанную в уравнении  . Записать общее уравнение прямой . Записать общее уравнение прямой  . .3.14. Прямые заданы уравнениями: 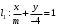 и и 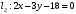 . При каком значении . При каком значении 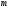 эти прямые будут параллельны. эти прямые будут параллельны.Задание 4. Решить следующие задания из задачника Клетеник Д.В. «Сборник задач по аналитической геометрии». № 210, 213, 215, 220(1), 223, 226, 227, 229, 232, 236, 242, 253(1). Ответы в конце задачника. 6.4. Задание №12 на практические занятия и самостоятельную работу. Решить самостоятельно: Задание 1. Дана точка: 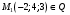 и вектор и вектор 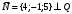 . Также дана точка . Также дана точка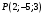 . .Записать пять уравнений плоскости  и найти отклонение и расстояние от точки и найти отклонение и расстояние от точки 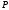 до плоскости до плоскости  . .Произвести возможные проверки. Задание 2. Даны три плоскости, заданные своими общими уравнениями. Определить имеют ли они единственную точку пересечения, если имеют то найти ее. Сделать проверку. Найти угол между плоскостями 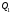 и и 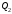 . .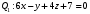 . .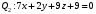 . .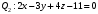 . .Задание 3. Проверить параллельность плоскостей 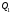 и и 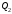 . Если плоскости параллельны, то найти расстояние между ними. . Если плоскости параллельны, то найти расстояние между ними.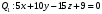 . .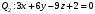 . .Задание 4. Решить следующие задания из задачника А.В.Ефимов, Б.П.Демидович «Сборник задач по математике», часть 1 «Линейная алгебра и основы математического анализа»: №2.180a. Задана плоскость 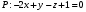 и точка и точка 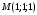 . Написать уравнение плоскости . Написать уравнение плоскости  , проходящей через точку , проходящей через точку 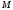 параллельно плоскости параллельно плоскости 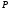 . .№2.181б. Задана плоскость 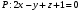 и две точки и две точки 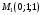 и и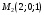 . Написать уравнение плоскости . Написать уравнение плоскости  , проходящей через эти точки перпендикулярно плоскости , проходящей через эти точки перпендикулярно плоскости 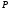 . .№2.182a. Написать уравнение плоскости  , проходящей через точку , проходящей через точку 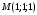 параллельно векторам параллельно векторам 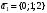 и и 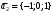 . .№2.183a. Написать уравнение плоскости  , проходящей через точки , проходящей через точки 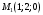 и и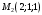 . параллельно вектору . параллельно вектору 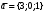 . .Ответы: №2.180a. 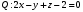 . №2.181б. . №2.181б. 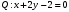 . .№2.182a. 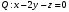 . №2.183a. . №2.183a. 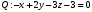 . .Решить дома: Задание 1. Записать пять уравнений плоскости  , если известно, что она отсекает по осям отрезки равные: по оси , если известно, что она отсекает по осям отрезки равные: по оси 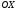 отрезок отрезок 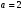 ; по оси ; по оси 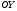 отрезок отрезок 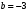 ; по оси ; по оси 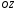 отрезок отрезок 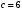 . Найти отклонение и расстояние от точки . Найти отклонение и расстояние от точки 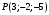 до плоскости до плоскости  . Произвести возможные проверки. . Произвести возможные проверки.Задание 2.Даны три плоскости, заданные своими общими уравнениями. Определить имеют ли они единственную точку пересечения, если имеют то найти ее. Сделать проверку. Найти угол между плоскостями 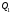 и и 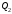 . .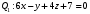 . .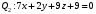 . .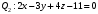 . .Задание 3. Проверить параллельность плоскостей 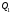 и и 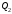 . Если плоскости параллельны, то найти расстояние между ними. . Если плоскости параллельны, то найти расстояние между ними.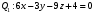 . .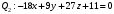 . .Задание 4. Решить следующие задания из задачника Клетеник Д.В. «Сборник задач по аналитической геометрии». № 915, 925(2), 926(3), 927(3), 932, 934. Ответы в конце задачника. 1 2 |
