Лекция_6_Прямая_на_плоскости_Плоскость-1. Лекция Прямая на плоскости
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
1 2 Лекция 6. 5. Прямая на плоскости. 5.1. Виды уравнений прямой на плоскости. 5.1.1. Уравнение прямой с нормальным вектором через точку. 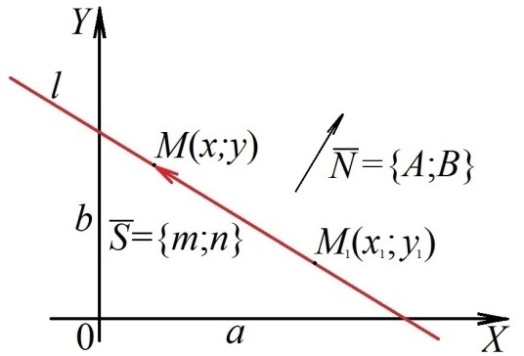 Пусть для прямой Пусть для прямой 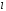 на плоскости известна точка, принадлежащая ей на плоскости известна точка, принадлежащая ей 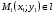 , и вектор , и вектор 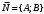 ей перпендикулярный. ей перпендикулярный.Вектор 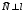 называется нормальным вектором прямой называется нормальным вектором прямой 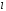 . Тогда для прямой может быть записано уравнение прямой с нормальным вектором через точку: . Тогда для прямой может быть записано уравнение прямой с нормальным вектором через точку: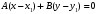 (1). (1).5.1.2. Общее уравнение прямой. Если в уравнении (1) раскрыть скобки и привести подобные, то будет получено общее уравнение прямой: 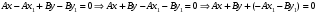 . .Обозначим число 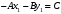 . Тогда уравнение примет вид: . Тогда уравнение примет вид: 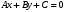 . Это и есть общее уравнение прямой: . Это и есть общее уравнение прямой: 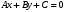 (2). (2).Если в этом уравнении 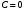 , то прямая проходит через начало координат. , то прямая проходит через начало координат.Если 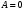 , то прямая параллельна оси , то прямая параллельна оси 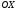 , а если еще и , а если еще и 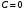 , то прямая совпадает с осью , то прямая совпадает с осью 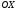 . .Если 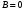 , то прямая параллельна оси , то прямая параллельна оси 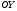 , а если еще и , а если еще и 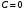 , то прямая совпадает с осью , то прямая совпадает с осью 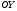 . .5.1.3. Каноническое уравнение прямой. Пусть для прямой 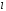 известна точка, принадлежащая ей известна точка, принадлежащая ей 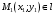 ,и вектор ,и вектор 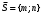 , ей параллельный или лежащий на ней. Вектор , ей параллельный или лежащий на ней. Вектор 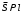 называется направляющим вектором прямой называется направляющим вектором прямой 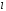 . Тогда для прямой . Тогда для прямой 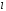 может быть записано каноническое уравнение прямой: может быть записано каноническое уравнение прямой: 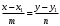 (3). (3).Если 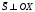 , то его проекция на эту ось равна , то его проекция на эту ось равна 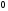 , следовательно, , следовательно, 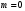 . В этом случае уравнение записывается в формальном виде, так как деление на ноль в действительных числах невозможно: . В этом случае уравнение записывается в формальном виде, так как деление на ноль в действительных числах невозможно: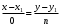 . .Аналогично, если 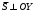 , то его проекция на эту ось равна , то его проекция на эту ось равна 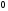 , следовательно, , следовательно, 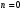 . В этом случае уравнение также записывается в формальном виде: . В этом случае уравнение также записывается в формальном виде: 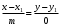 . .5.1.4. Параметрические уравнения прямой. Приравняем каноническое уравнение (3) к значению некоторого параметра 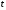 : :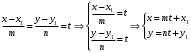 . .Полученная система описывает параметрические уравнения прямой: 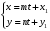 (4). (4).5.1.5. Уравнение прямой через две точки. Пусть для прямой 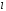 известны две точки, ей принадлежащие: известны две точки, ей принадлежащие: 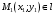 и и 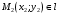 . Тогда в качестве направляющего вектора вектор . Тогда в качестве направляющего вектора вектор 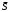 можно взять вектор можно взять вектор 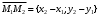 . При этом каноничекое уравнение запишется в виде уравнения прямой через две точки: . При этом каноничекое уравнение запишется в виде уравнения прямой через две точки: 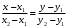 (5). (5).5.1.6. Уравнение прямой через данную точку в заданном направлении. Рассмотри на плоскости 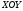 прямую прямую 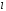 непараллельную оси непараллельную оси 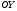 . .Е 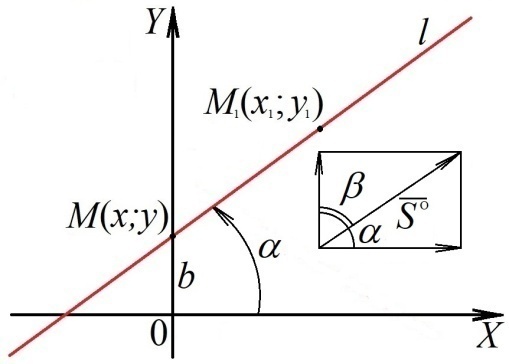 е положение определяется углом е положение определяется углом  между прямой и осью между прямой и осью 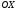 и известной точкой и известной точкой 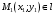 . В качестве направляющего вектора возьмем единичный вектор (орт) . В качестве направляющего вектора возьмем единичный вектор (орт) 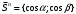 . .Так как 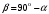 , то , то 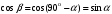 . Следовательно, . Следовательно, 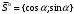 Тогда каноническое уравнение запишется так: 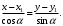 Выразим из этого уравнения Выразим из этого уравнения 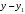 : : 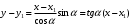 . .Коэффициент 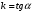 называется угловым коэффициентом прямой. В результате получим уравнение прямой через заданную точку в заданном направлении: называется угловым коэффициентом прямой. В результате получим уравнение прямой через заданную точку в заданном направлении: 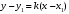 (6). (6).Если прямая 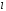 параллельна оси параллельна оси 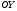 , то , то 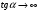 , и уравнение в таком виде записано быть не может. , и уравнение в таком виде записано быть не может.5.1.7. Уравнение прямой с угловым коэффициентом. Пусть прямая 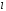 составляет с осью составляет с осью 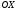 угол угол  и пересекает ось и пересекает ось 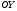 в точке в точке 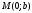 . Тогда уравнение (6) примет вид: . Тогда уравнение (6) примет вид: 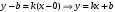 . Это и есть уравнение прямой с угловым коэффициентом: . Это и есть уравнение прямой с угловым коэффициентом: 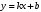 (7). (7).5.1.8. Уравнение прямой в отрезках. Если прямая 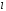 отсекает по оси отсекает по оси 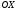 отрезок отрезок  , а по оси , а по оси 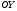 отрезок отрезок 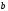 , то она проходит через точки: , то она проходит через точки: 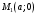 и и 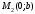 . .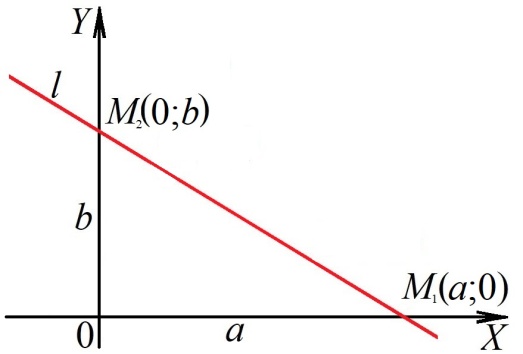 Уравнение через две точки перепишется так: 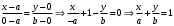 . .Это и есть уравнение прямой в отрезках: 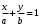 (8). (8).5.1.9. Нормальное уравнение прямой. Пусть прямая задана в общем виде (2): 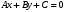 . Найдем нормирующий множитель: . Найдем нормирующий множитель: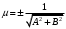 , где знак , где знак 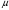 выбирается противоположным знаку коэффициента выбирается противоположным знаку коэффициента 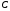 в уравнении (2). в уравнении (2).Умножим общее уравнение на этот коэффициент и получим нормальное уравнение прямой: 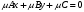 (9). (9).Нормальное уравнение прямой обладает следующим свойством. Если в него подставить координаты произвольной точки плоскости 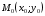 , то будет получено отклонение , то будет получено отклонение 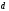 от точки от точки 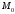 до прямой до прямой 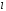 : : 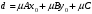 . .Если 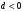 , то точка , то точка 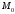 и прямая и прямая 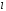 лежат по одну сторону от начала координат, а если лежат по одну сторону от начала координат, а если 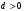 , то по разные. При этом модуль отклонения равен расстоянию , то по разные. При этом модуль отклонения равен расстоянию  от точки от точки 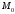 до прямой до прямой 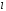 : : 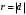 . .Если отклонение искать не требуется, а достаточно найти лишь расстояние от точи 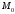 до прямой до прямой 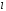 , то можно воспользоваться следующей формулой: , то можно воспользоваться следующей формулой: 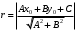 (10). (10).5.2. Взаимное расположение прямых на плоскости. Пусть для прямой  известны: известны:нормальный вектор 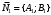 , направляющий вектор , направляющий вектор 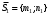 и угловой коэффициент и угловой коэффициент 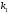 ; ;для прямой  : :нормальный вектор 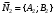 , направляющий вектор , направляющий вектор 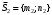 и угловой коэффициент и угловой коэффициент 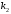 ; ;тогда: 1. Прямые  и и  параллельны, если: параллельны, если:- 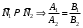 или или 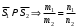 ; ;- 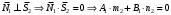 или или 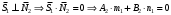 ; ;- 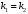 . .2. Прямые  и и  перпендикулярны если: перпендикулярны если:- 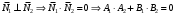 или или 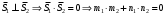 ; ; - 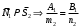 или или 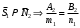 ; ;- 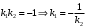 . .3. Если прямые  и и  не параллельны, то они имеют единственную точку пересечения, которая находится из решения системы, составленной из общих уравнений этих прямых: не параллельны, то они имеют единственную точку пересечения, которая находится из решения системы, составленной из общих уравнений этих прямых: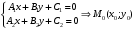 - точка пересечения прямых. - точка пересечения прямых.4. Если прямые  и и  не перпендикулярны, то угол между прямыми может быть найден по формуле: не перпендикулярны, то угол между прямыми может быть найден по формуле: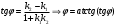 . .Пример 1. Записать девять уравнений прямой  , если точка , если точка 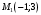 принадлежит прямой, а вектор принадлежит прямой, а вектор 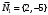 ей перпендикулярен. ей перпендикулярен.1. Воспользуемся формулой (1) и запишем уравнение прямой с нормальным вектором через точку: 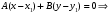 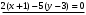 (1) (1)2. Раскроем в уравнении (1) скобки и получим общее уравнение (2). 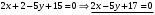 (2) (2)3. Выразим 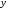 из общего уравнения (2) и получим уравнение с угловым коэффициентом (7). из общего уравнения (2) и получим уравнение с угловым коэффициентом (7).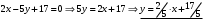 (7) (7)Из уравнения (7) следует, что угловой коэффициент прямой 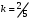 , а отрезок, отсекаемый ей по оси , а отрезок, отсекаемый ей по оси 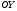 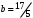 . .4. С учетом найденного углового коэффициента 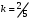 и известной точки и известной точки 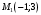 запишем уравнение прямой через заданную точку в заданном направлении (6): запишем уравнение прямой через заданную точку в заданном направлении (6):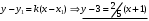 (6) (6)5. Выведем из общего уравнения (2) уравнение в отрезках (8). Для этого разделим уравнение (2) на свободный член 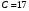 . .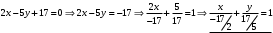 (8) (8)Из уравнения (8) следует, что отрезок, отсекаемый прямой по оси 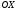 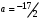 , а отрезок, отсекаемый ей по оси , а отрезок, отсекаемый ей по оси 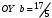 . .6. Для того чтобы записать уравнение прямой через две точки (5) найдем координаты второй точки из общего уравнения (2), придав какое-либо значение одной из координат, например 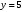 . .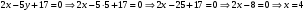 . .Таким образом, в качестве второй точки прямой может быть взята точка 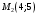 . Тогда уравнение прямой через две точки запишется так: . Тогда уравнение прямой через две точки запишется так:  (5) . (5) .7. Посчитаем знаменатели в уравнении (5) и получим каноническое уравнение прямой (3).  (3) . (3) .Из уравнения (3) следует, что направляющий вектор прямой  . .8. Найдем параметрические уравнения прямой (4). Для этого приравняем каноническое уравнение (3) к значению параметра  : : 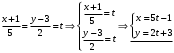 (4) . (4) .9. Запишем нормальное уравнение прямой (9). Для этого найдем нормирующий множитель, взяв его знак противоположным знаку свободного члена 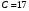 . .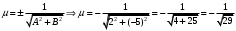 . .Тогда нормальное уравнение (9) запишется так: 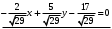 (9) . (9) .Пример 2. Даны две точки, принадлежащие прямой  : : 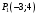 и и 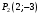 . Найти отклонение и расстояние от точки . Найти отклонение и расстояние от точки 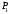 до прямой до прямой  из Примера 1. Если прямые из Примера 1. Если прямые  и и  не параллельны, то найти их точку пересечения и угол между прямыми не параллельны, то найти их точку пересечения и угол между прямыми  и и  . .1. Воспользуемся нормальным уравнением (9) прямой  . Подставим в это уравнение координатыточки . Подставим в это уравнение координатыточки 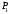 и найдем отклонение этой точки от прямой и найдем отклонение этой точки от прямой  . .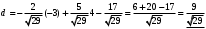 . .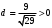 - точка - точка 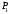 и начло координат лежат по разные стороны от прямой и начло координат лежат по разные стороны от прямой  . .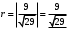 - расстояние от точки - расстояние от точки 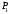 до прямой до прямой  . .2. Найдем уравнение прямой  через две точки: через две точки: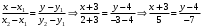 . .Тогда общее уравнение прямой  : :  . .Следовательно, нормальный вектор прямой  : : 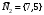 . Нормальный вектор прямой . Нормальный вектор прямой  : :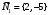 . .Прямые  и и  не параллельны, так как их нормальные вектора неколлинеарны: не параллельны, так как их нормальные вектора неколлинеарны: 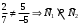 . .Тогда прямые  и и  имеют единственную точку пересечения. Найдем ее, решив систему, составленную из общих уравнений этих прямых: имеют единственную точку пересечения. Найдем ее, решив систему, составленную из общих уравнений этих прямых: 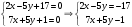 . .Метод Гаусса: 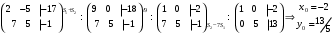 . .Точка пересечения прямых 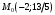 . Правильность нахождения точки . Правильность нахождения точки 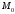 можно проверить подстановкой ее координат в уравнения обеих прямых. можно проверить подстановкой ее координат в уравнения обеих прямых.3. Найдем угловой коэффициент прямой  : : 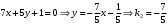 . .Воспользуемся формулой для нахождения тангенса угла между прямыми 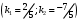 : :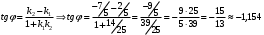 . .Тогда: 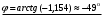 . .6. Плоскость в пространстве. 6.1. Виды уравнений плоскости в пространстве. 6.1. 1. Уравнение плоскости с нормальным вектором через точку.  Пусть для плоскости  известна точка, принадлежащая ей известна точка, принадлежащая ей  и вектор и вектор  ей перпендикулярный. Вектор ей перпендикулярный. Вектор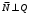 называется нормальным вектором плоскости называется нормальным вектором плоскости  . Тогда для плоскости . Тогда для плоскости  может быть записано уравнение с нормальным вектором через точку: может быть записано уравнение с нормальным вектором через точку: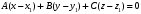 (10). (10).6.1.2. Общее уравнение плоскости. Если в уравнении (10) раскрыть скобки и привести подобные, то будет получено общее уравнение плоскости: 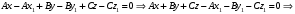 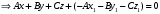 . .Обозначим число 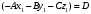 . Тогда уравнение примет вид: . Тогда уравнение примет вид: 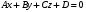 . Это и есть общее уравнение плоскости: . Это и есть общее уравнение плоскости: 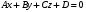 (12). (12).Если в этом уравнении 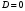 , то плоскость проходит через начало координат. , то плоскость проходит через начало координат.Если один из коэффициентов 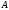 или или 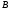 , или , или 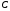 равен нулю, то плоскость параллельна соответствующей оси: равен нулю, то плоскость параллельна соответствующей оси: 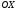 или или 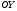 или или 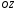 . Если при этом еще и . Если при этом еще и 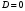 , то плоскость проходит через соответствующую ось. , то плоскость проходит через соответствующую ось.Если любая пара коэффициентов 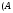 и и 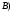 или или 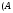 и и 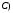 , или , или 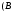 и и 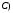 равна нулю, то плоскость параллельна соответствующей координатной плоскости: равна нулю, то плоскость параллельна соответствующей координатной плоскости: 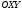 или или 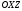 или или 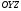 . Если при этом еще и . Если при этом еще и 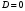 , то плоскость совпадает с соответствующей координатной плоскостью. , то плоскость совпадает с соответствующей координатной плоскостью.6.1.3. Уравнение плоскости в отрезках. Если плоскость отсекает по оси 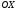 отрезок отрезок  , по оси , по оси 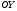 отрезок отрезок 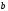 , а по оси , а по оси 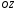 отрезок отрезок  , то ее уравнение может быть записано в виде уравнения плоскости в отрезках: , то ее уравнение может быть записано в виде уравнения плоскости в отрезках: 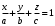 (13) . (13) .6.1.4. Уравнение плоскости через три точки. Через любые три точки пространства, не лежащие на одной прямой, можно всегда провести плоскость, причем единственным образом. Верно и обратное утверждение: три точки, не лежащие на одной прямой, принадлежат одной плоскости. Пусть для плоскости  известны три точки ей принадлежащие: известны три точки ей принадлежащие: 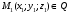 , , 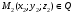 и и  . Тогда уравнение плоскости через три точки можно записать в виде определителя третьего порядка: . Тогда уравнение плоскости через три точки можно записать в виде определителя третьего порядка:  (14) . (14) .Если этот определитель раскрыть и привести подобные члены, то будет получено общее уравнение плоскости (12). 6.1.5. Нормальное уравнение плоскости. Пусть плоскость задана общим уравнением:  . Найдем нормирующий множитель: . Найдем нормирующий множитель: , где знак , где знак 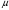 выбирается противоположным знаку коэффициента выбирается противоположным знаку коэффициента 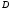 в уравнении. в уравнении.Умножим общее уравнение на этот множитель и получим нормальное уравнение плоскости: 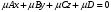 (15). (15).Нормальное уравнение плоскости обладает следующим свойством. Если в него подставить координаты произвольной точки плоскости 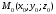 , то будет получено отклонение , то будет получено отклонение 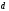 от точки от точки 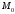 до плоскости до плоскости  : :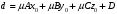 . .Если 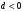 , то точка , то точка 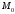 и плоскость и плоскость  лежат по одну сторону от начала координат, а если лежат по одну сторону от начала координат, а если 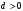 , то по разные. При этом модуль отклонения равен расстоянию , то по разные. При этом модуль отклонения равен расстоянию  от точки от точки 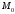 до плоскости до плоскости  : : 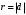 . .Если отклонение искать не требуется, а достаточно найти лишь расстояние от точи 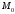 до плоскости до плоскости  , то можно воспользоваться следующей формулой: , то можно воспользоваться следующей формулой: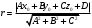 (16). (16).6.2. Взаимное расположение плоскостей в пространстве. Пусть две плоскости заданы своими общими уравнениями: 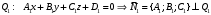 . .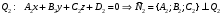 , где , где 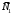 и и 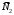 - нормальные вектора этих плоскостей, тогда: - нормальные вектора этих плоскостей, тогда:1. Плоскости 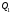 и и 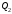 параллельны, если коллинеарны их нормальные вектора: параллельны, если коллинеарны их нормальные вектора: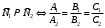 . .Замечание. Для того, чтобы найти расстояние между параллельными плоскостями, достаточно найти расстояние от любой точки, принадлежащей одной из плоскостей, до второй плоскости. 2. Плоскости 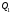 и и 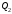 перпендикулярны, если перпендикулярны их нормальные вектора: перпендикулярны, если перпендикулярны их нормальные вектора: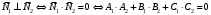 . .3. Если плоскости 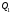 и и 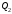 не параллельны, то они пересекаются по некоторой прямой. Координаты точек этой прямой удовлетворяют бесчисленному множеству решений системы, составленной из общих уравнений этих плоскостей: не параллельны, то они пересекаются по некоторой прямой. Координаты точек этой прямой удовлетворяют бесчисленному множеству решений системы, составленной из общих уравнений этих плоскостей: 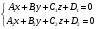  линия пересечения плоскостей линия пересечения плоскостей 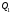 и и  . .4  . В общем случае плоскости . В общем случае плоскости  и и  не перпендикулярны и не параллельны. За угол между двумя плоскостями принимают один из двухгранных углов, образуемых ими при пересечении. Угол между нормальными векторами не перпендикулярны и не параллельны. За угол между двумя плоскостями принимают один из двухгранных углов, образуемых ими при пересечении. Угол между нормальными векторами 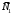 и и 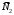 численно равен одному из этих двухгранных углов. Поэтому угол между плоскостями численно равен одному из этих двухгранных углов. Поэтому угол между плоскостями 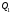 и и 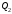 можно искать через косинус угла между их нормальными векторами: можно искать через косинус угла между их нормальными векторами: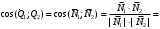 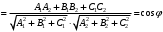 (17). (17).Тогда 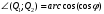 . .5. Если имеется еще и третья известная плоскость 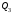 : :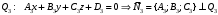 , ,то возможен случай, когда три плоскости пересекутся в одной точке. Для этого необходимо и достаточно, чтобы определитель, составленный из координат нормальных векторов этих плоскостей, был не равен нулю: 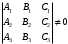 . .При этом точка пересечения трех плоскостей найдется из решения системы, составленной из общих уравнений этих плоскостей: 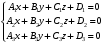 . .Пример 1. Даны четыре точки: 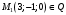 ; ; 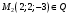 ; ; 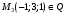 и и 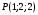 . Записать пять уравнений плоскости . Записать пять уравнений плоскости  и найти отклонение и расстояние от точки и найти отклонение и расстояние от точки 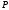 до плоскости до плоскости  . Произвести возможные проверки. . Произвести возможные проверки.1. Воспользуемся уравнением плоскости через три точки (14): 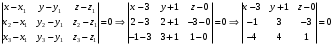 (14). (14).2. Раскроем определитель, приведем подобные члены и получим общее уравнение плоскости (12): 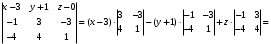 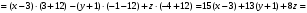 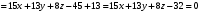 . .Таким образом, общее уравнение плоскости  : : 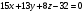 (12) . (12) .Для проверки правильности нахождения общего уравнения (12) подставим в него поочередно координаты точек плоскости 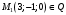 ; ; 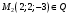 ; ; 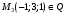 . Должны получить три тождества. . Должны получить три тождества.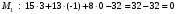 Верно. Верно.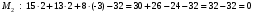 Верно. Верно.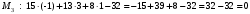 Верно. Верно.Общее уравнение плоскости  уравнение найдено верно. уравнение найдено верно.3. Запишем уравнение плоскости с нормальным вектором через точку (10). Из найденного общего уравнения (2) следует, что нормальный вектор 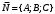 плоскости плоскости  равен: равен: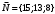 . В качестве точки . В качестве точки 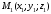 можно выбрать любую из трех известных точек: можно выбрать любую из трех известных точек: 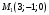 ; ; 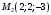 или или 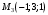 . Выберем, например, точку . Выберем, например, точку 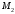 , подставив ее координаты в уравнение (10): , подставив ее координаты в уравнение (10):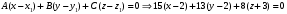 (10). (10).Если раскрыть скобки в полученном уравнении , то не зависимо от выбора точки, будет получено общее уравнение плоскости (2). Проверка: 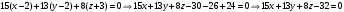 Верно. Верно.4. Запишем уравнение плоскости в отрезках (13). Для этого преобразуем общее уравнение плоскости следующим образом: 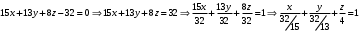 (13) (13)Таким образом, плоскость  отсекает по осям следующие отрезки: отсекает по осям следующие отрезки:по оси 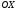 отрезок отрезок 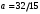 ; по оси ; по оси 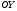 отрезок отрезок 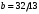 ; по оси ; по оси 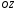 отрезок отрезок 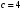 . . Следовательно, плоскость проходит через точки 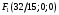 ; ; 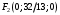 ; ; 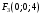 . Для проверки составим уравнение плоскости через три точки и приведем его к общему виду. Должны получить общее уравнение, полученное в пункте 2. . Для проверки составим уравнение плоскости через три точки и приведем его к общему виду. Должны получить общее уравнение, полученное в пункте 2.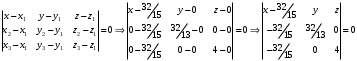 . .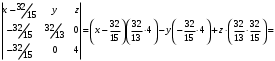 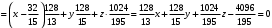 . .Умножим уравнение на 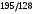 , получим: , получим: 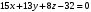 . .Результат совпал с общим уравнением плоскости. Уравнение в отрезках найдено верно. 5. Запишем нормальное уравнение плоскости (15), для этого используем общее уравнение (12). 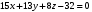 , где , где 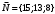 . .Найдем нормирующий множитель, взяв его знак противоположным знаку свободного члена 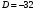 . .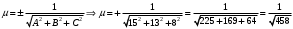 . .Тогда нормальное уравнение (15) запишется так: 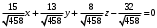 (15). (15). 1 2 |
