Првво. Лекция 8. Лекция Замечательные пределы. Непрерывность функции
 Скачать 134.99 Kb. Скачать 134.99 Kb.
|
Замечательные пределы. Непрерывность функции. Точки разрыва функции и их классификация. 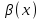 при при 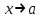 ; ;б) при 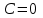 , , 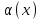 называют бесконечно малой более высокого порядка, чем называют бесконечно малой более высокого порядка, чем 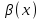 . Обозначение: . Обозначение: 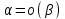 . .2. Непрерывность функции. Свойства функций, непрерывных в точке. Непрерывность функции в точке и на промежутке. Пусть функция 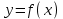 определена в точке определена в точке 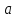 и некоторой ее окрестности. и некоторой ее окрестности.Определение 1. Функция 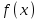 называется непрерывной в точке называется непрерывной в точке 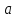 , если , если 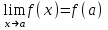 . .На практике, при выяснении непрерывности функции в точке 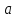 , достаточно проверить следующие три условия: , достаточно проверить следующие три условия: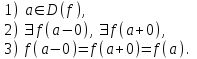 (*) (*)1. Функция f(x) называется непрерывной в точке 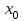 , если она удовлетворяет следующим условиям: , если она удовлетворяет следующим условиям: 1) определена в точке 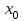 ; ; 2) имеет конечный предел при 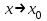 ; ; 3) этот предел равен значению функции в этой точке: 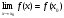 . .2. Если функции f(x) и φ(х) непрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке. 3. Если функция y=f(u) непрерывна в точке 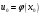 , а функция u=φ(x) непрерывна в точке , а функция u=φ(x) непрерывна в точке 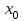 , то сложная функция , то сложная функция 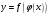 непрерывна в точке непрерывна в точке 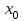 . .4. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. 5. Все элементарные функции непрерывны во всех точках, где они определены. Теорема 1. Если функции 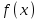 и и 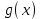 непрерывны в точке непрерывны в точке 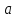 , то функции , то функции 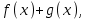 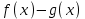 , , 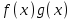 , , 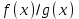 , также непрерывны в точке , также непрерывны в точке 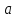 (частное – при условии (частное – при условии 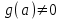 ). ).Теорема 2. Пусть функция 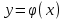 непрерывна в точке непрерывна в точке 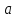 , а функция , а функция 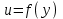 непрерывна в точке непрерывна в точке 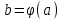 . Тогда сложная функция . Тогда сложная функция 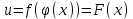 непрерывна в точке непрерывна в точке 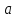 . .Замечание. Теорема 2 может быть записана в виде 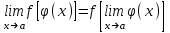 , ,т.е. под знаком непрерывной функции можно переходить к пределу. Теорема 3. Функция 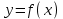 непрерывна в точке непрерывна в точке 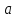 тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 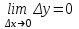 . .Определение 2. Функция 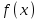 называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.Теорема 4. Всякая элементарная функция непрерывна в своей области определения. 3.Точки разрыва функции и их классификация. Точки, в которых нарушается непрерывность функции, называют точками разрыва. На практике это означает нарушение хотя бы одного из указанных выше (*) трех условий непрерывности. Определение 3. Пусть 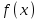 определена в некоторой окрестности точки определена в некоторой окрестности точки 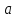 за исключением, быть может, самой точки за исключением, быть может, самой точки 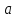 . Точка . Точка 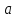 называется точкой разрыва. называется точкой разрыва.Если не выполнено определение непрерывности, то функция в точке 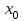 терпит разрыв, причем: терпит разрыв, причем:а) если оба односторонних предела 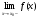 и и 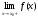 конечны, равны между собой, но не равны f( конечны, равны между собой, но не равны f(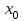 ), то ), то 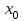 - точка устранимого разрыва первого рода; - точка устранимого разрыва первого рода;б) если оба односторонних предела 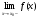 и и 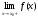 конечны, но не равны между собой, то конечны, но не равны между собой, то 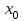 - точка неустранимого разрыва первого рода; - точка неустранимого разрыва первого рода;в) если хотя бы один из односторонних пределов 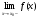 или или 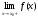 бесконечен или не существует вовсе то бесконечен или не существует вовсе то 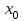 - точка разрыва второго рода. - точка разрыва второго рода.Пример 1. Найти область определения функции 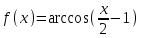 . .Решение. Данная функция определена, если 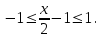 Решая неравенства, получаем область определения функции Решая неравенства, получаем область определения функции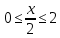 или или 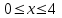 , т.е. , т.е. 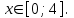 Пример 2. Найти точки разрыва функции. 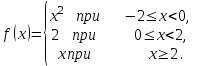 Решение. Каждая из трех функций 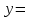 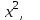 y = x, y= 2 непрерывны в области определения. Поэтому разрыв возможен только на стыке промежутков, то есть в точках y = x, y= 2 непрерывны в области определения. Поэтому разрыв возможен только на стыке промежутков, то есть в точках 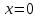 , ,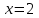 . Для точки . Для точки 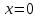 имеем: имеем: 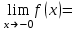 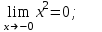 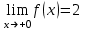 . Следовательно, . Следовательно, 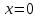 является точкой разрыва функции первого рода. Для точки является точкой разрыва функции первого рода. Для точки 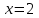 имеем: имеем: 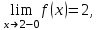 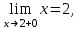 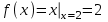 . Это означает, что функция в точке . Это означает, что функция в точке 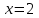 непрерывна. непрерывна.Контрольные вопросы: 1. Дайте определение функции. Что называется областью определения функции? 2. Каковы основные способы задания функции? Приведите примеры. 3. Какая функция называется элементарной, сложной? Приведите примеры. 4. Сформулируйте определения предела последовательности, предела функции при стремлении аргумента к некоторому конечному пределу. 5. Какая функция называется бесконечно малой и каковы ее основные свойства? 6. Какой предел называется первым замечательным пределом? Сформулируйте определение числа е. 7. Сравнение бесконечно малых, теоремы о пределах функций. 8. Сформулируйте определения непрерывности функции в точке и на отрезке. 9. Какие точки называются точками разрыва функции?Литература: 1. Под редакцией проф. Кремера Н. Ш. Высшая математика для экономистов.- М: ЮНИТИ/UNITY, 2010. 2. Казешев А.К., Нурпеисов С.А. Математика для экономистов. Учебное пособие./- Алматы: 2008. Под общей редакцией д.э.н., проф. Рахметовой Р.У. 3. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. Ч.1,2. М.: ОНИКС, Мир и Образование, 2009. |

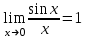 называется первым замечательным пределом. Отметим, что этот предел является неопределенностью типа
называется первым замечательным пределом. Отметим, что этот предел является неопределенностью типа 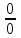 .
.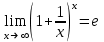 или
или 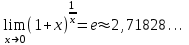 называется вторым замечательным пределом.
называется вторым замечательным пределом.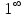 . Для его отыскания при
. Для его отыскания при 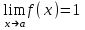 , и
, и 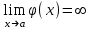 , справедлива вычислительная формула
, справедлива вычислительная формула 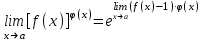 (*)
(*)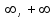 или
или 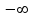 .
. 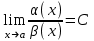 . Тогда:
. Тогда: 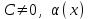 и
и 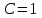 бесконечно малые
бесконечно малые