Практическая работа Линейная алгебра. Линейная алгебра
 Скачать 36.88 Kb. Скачать 36.88 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ __________ЛИНЕЙНАЯ АЛГЕБРА__________ Группа Кс19Э271 Студент А.И. Юшкова МОСКВА 2020 Задачи. 1. Найти сумму матриц: 1.1. А= 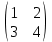 В= В=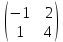 А+В= 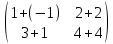 А+В= 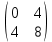 1.2. А= 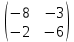 В= В= 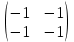 А+В= 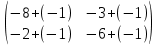 А+В= 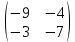 2. Найти произведение матриц: 2.1. А= 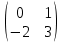 В= В= 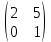 А·В= 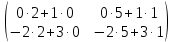 А·В= 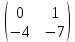 2.1. А= 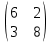 В= В= 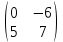 А·В= 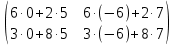 А·В= 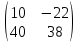 3. Найти определители матриц: 3.1. А= 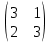 |А|=3·3-1·2=7 3.2. А= 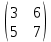 |А|=3·7  6·5= 6·5= 9 9 4. Решить систему уравнений: 4.1. 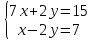 Методом подстановки выражаем из второго уравнение x: x=7+2y Подставляем в первое уравнение значение x: 7·(7+2y)+2y=15 49+14y+2y=15 16y=15  49 49y= 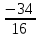 = =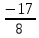 Находим значение x: x=7+2· 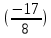 =7 =7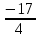 = =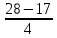 = =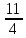 Ответ: x= 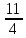 ; y= ; y=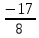 . .Решим систему уравнений методом Крамера: Ищем определитель второго порядка |А|= 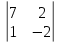 =7·( =7·( 2) 2) 1·2= 1·2= 16 16Ищем определитель первого неизвестного | 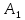 |= |=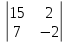 =15·( =15·( 2) 2) 7·2= 7·2=  44 44Ищем определитель второго неизвестного | 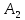 |= |=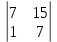 =7·7 =7·7 1·15= 34 1·15= 34Первое неизвестное x равно  44 / 44 /  16 = 16 = 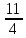 , второе неизвестное y равно 34 / , второе неизвестное y равно 34 /  16 = 16 = 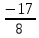 . .Ответ: x= 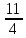 ; y= ; y=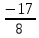 . .4.2. 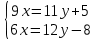  Решим систему уравнений методом Крамера: Ищем определитель второго порядка |А|= 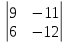 =9·( =9·( 12) 12) 6·( 6·( 11)= 11)= 108+66= 108+66= 42 42Ищем определитель первого неизвестного | 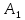 |= |=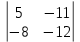 =5·( =5·( 12) 12) ( ( 8)·(-11)= 8)·(-11)= 60 60 88= 88=  148 148Ищем определитель второго неизвестного | 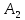 |= |=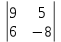 =9·( =9·( 8) 8) 6·5= 6·5=  72 72 30= 30= 102 102Первое неизвестное x равно  148 / 148 /  42 = 42 = 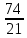 , второе неизвестное y равно , второе неизвестное y равно  102 / 102 /  42 = 42 = 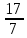 . .Ответ: x= 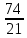 ; y= ; y=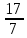 . .5. Для заданных векторов найти смешанное произведение [ 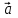 · ·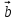 ]· ]·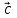 5.1. 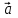 =(1; =(1; 2;1) 2;1) 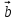 =(2;1; =(2;1; 2) 2) 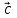 =(1;1;1) =(1;1;1)([ 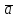 · ·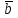 ]· ]·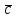 )=1· )=1·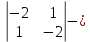 1· 1·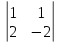 + 1· + 1·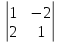 ([ 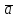 · ·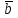 ]· ]·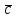 )= 1·(4 )= 1·(4 1) 1) 1·( 1·( 2 2 2)+ 1·(1+4)= 3+4+5= 12 2)+ 1·(1+4)= 3+4+5= 12Ответ: ([ 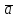 · ·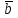 ]· ]·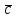 )= 12. )= 12.5.2. 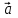 =(1;1;2) =(1;1;2) 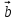 =(1; =(1; 1;3) 1;3) 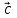 =( =( 2; 2; 2;2) 2;2)([ 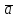 · ·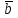 ]· ]·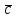 )= )=  2· 2·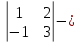 ( ( 2)· 2)·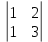 + 2· + 2·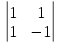 ([ 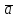 · ·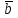 ]· ]·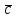 )= ( )= ( 2)·(3+2) 2)·(3+2) ( ( 2)·(3 2)·(3 2)+ 2·( 2)+ 2·( 1 1 1)= -10+2-4= 1)= -10+2-4=  12 12Ответ: ([ 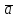 · ·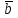 ]· ]·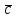 )= )=  12. 12. |
