Высшая математика. Линейная алгебра. "Линейные операторы, собственные числа и собственные векторы матрицы"

• Название: "Линейные операторы, собственные числа и собственные векторы матрицы"
• Анкор: Высшая математика. Линейная алгебра
• Дата: 10.12.2021
• Размер: 29.56 Kb.
• Имя файла: crossword.docx
• Тип: Документы; #299023
• страница: 3 из 3

Раздел 2. Тема 1 : " Метод координат на плоскости и пространстве".

Инструкция: Соотнесите написанное в столбцах 1 и 2.

ТЕРМИН	ЗНАЧЕНИЕ
А) Прямоугольная система координат	1) Направленный отрезок прямой, для которго указано, какая из его граничных точек является концом, а какая началом
Б) Скалярное произведение	2) Двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами - полярным углом и полярным радиусом
В) Полярная система координат	3) Система координат с взаимно перпендикулярными осями на плоскости или в пространстве
Г) Метод координат	4) Операция над двумя векторами, результатом которой является число, не зависящее от системы координат и характеризующее длины векторов и угол между ними
Д) Координата	5) Способ определять положение точки или тела с помощью чисел или других символов
Ж) Вектор	6)Число, определяющее положение точки в системе координат

Ответ:

А	Б	В	Г	Д	Ж

Лай А.И.

Раздел 2. Тема 1 : " Метод координат на плоскости и пространстве".

Ответ:

А	Б	В	Г	Д	Ж
3	4	2	5	6	1

Лай А.И.

Раздел 3. Введение в математический анализ. Тема 1 : "Множества и операции над ними".

Название операции	Обозначение	Изображение кругами Эйлера	Определение	Символическая запись
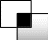
Пересечение множеств	А⋂В	А В	Те и только те элементы, которые принадлежат одновременно А и В	А⋂В=(х∣х∊А и х⊄∆∊В)∖
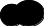
Объединение множеств	А⋃В	А В	Те и только те элементы. которые принадлежат хотя бы одному из множеств А и В	А⋃В=(х∣х∊А или х∊В)
Разность множеств	А\В	А В	Те и только те элементы множества А. которые не принадлежат В	А∖В=(х∣х⊄А и х⊄В)
Дополнение к множеству А	Ā=Α= =U\A		Те и только те элементы, которые не принадлежат множеству А (т.е. дополняют его до универсального U)	Ā=(х∣х⊄А)=⋃∖А
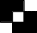
Симметрическая разность	А b B	А В	Те и только те элементы, которые принадлежат одному из множеств: А либо В, но не являются общими элементами	А∆В= =(А∖В)⋃(В∖А)= =(А⋃В)∖(А⋂В)

Лай А.И.