Заказ №1346. Линейных уравнений. Доказать её совместность и решить двумя способами 1 методом Гаусса 2 средствами матричного исчисления

• Название: Линейных уравнений. Доказать её совместность и решить двумя способами 1 методом Гаусса 2 средствами матричного исчисления
• Дата: 25.11.2018
• Размер: 1.13 Mb.
• Имя файла: Заказ №1346.doc
• Тип: Документы; #57639

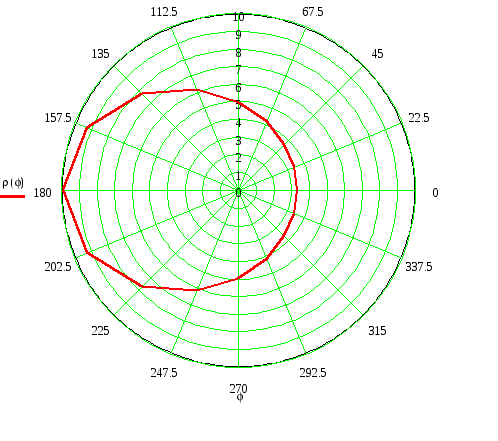
Вариант №7
7. Дана система линейных уравнений. Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.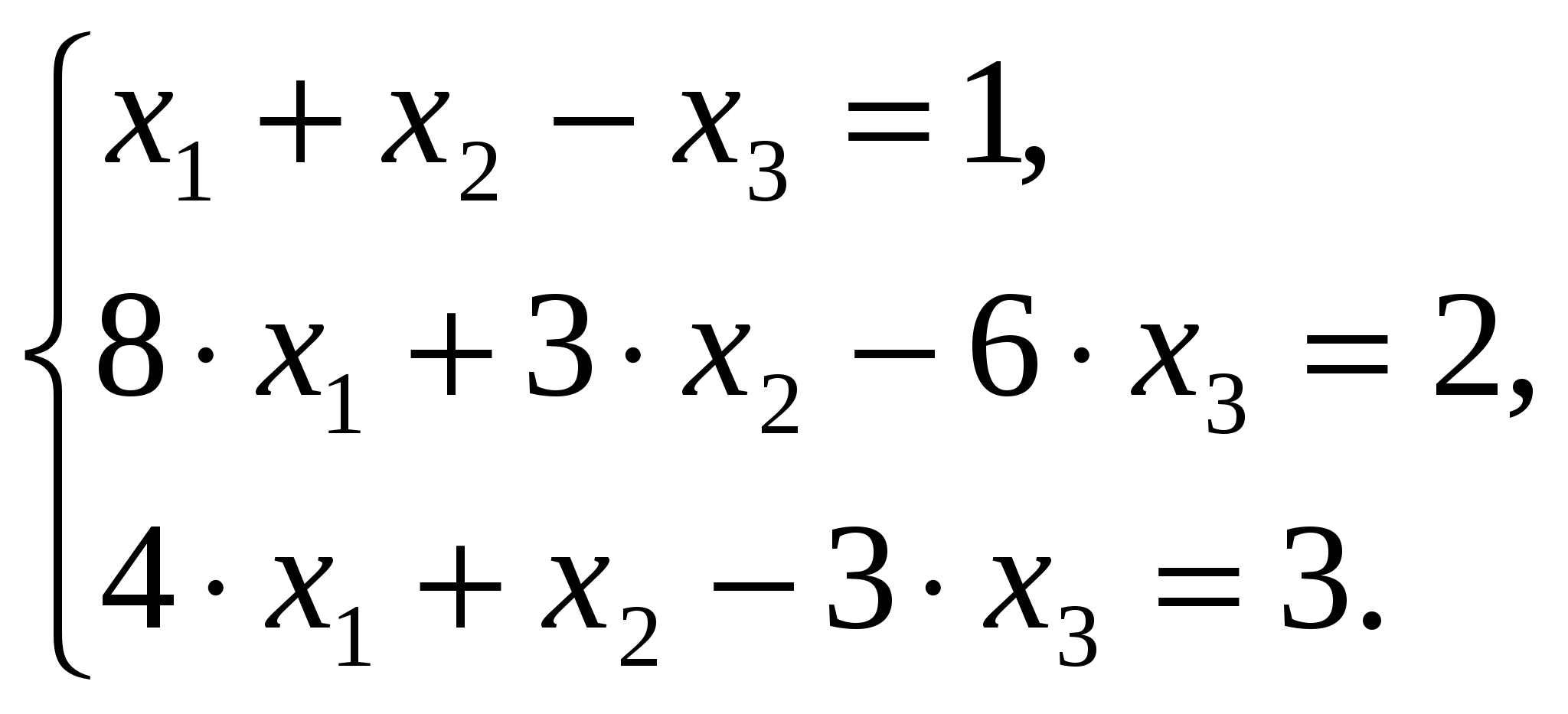

1. Запишем расширенную матрицу системы: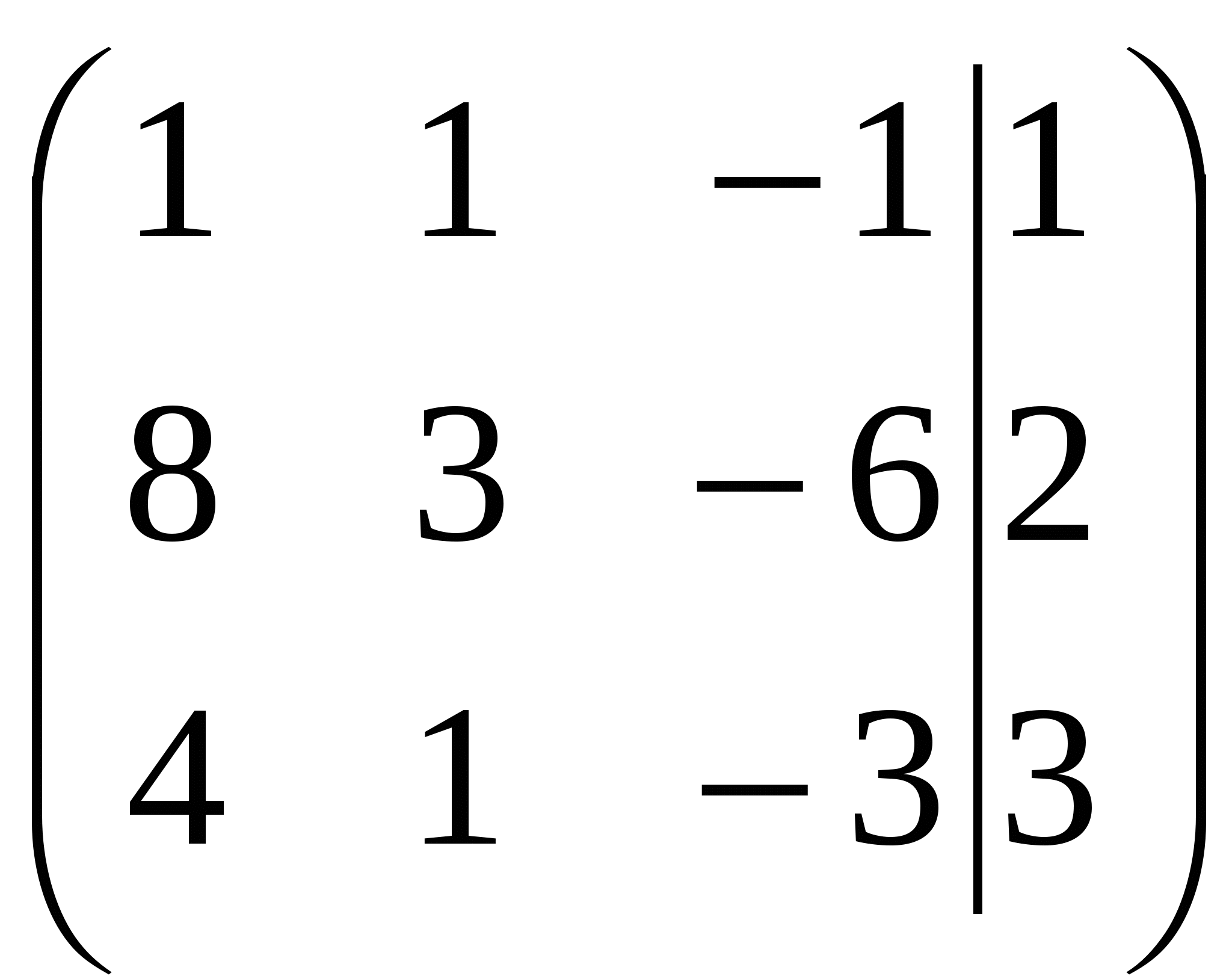

;

2. Умножим первую строку на 8: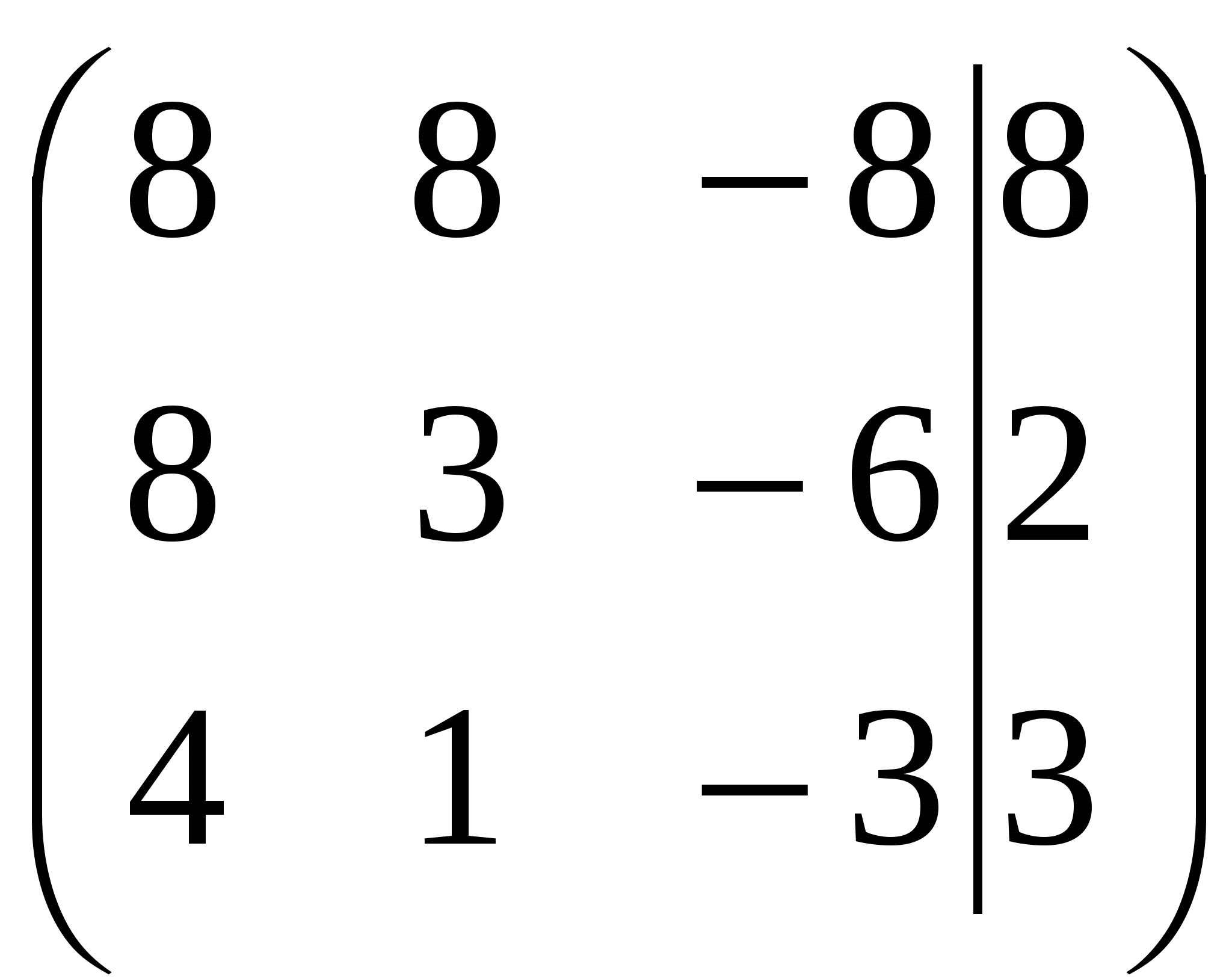

;

3. Умножим вторую строку на :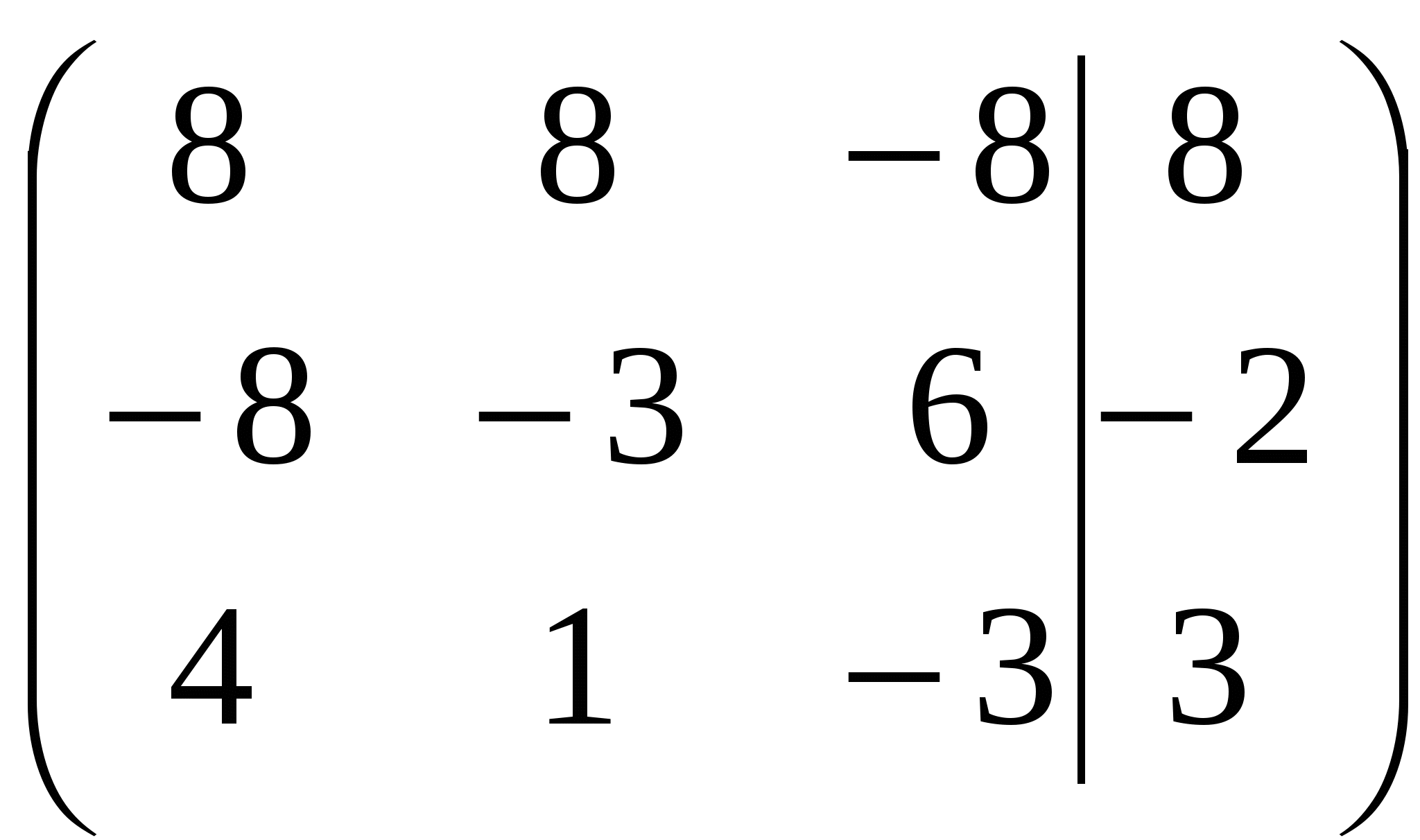

;

4. Прибавим вторую строку к первой строке: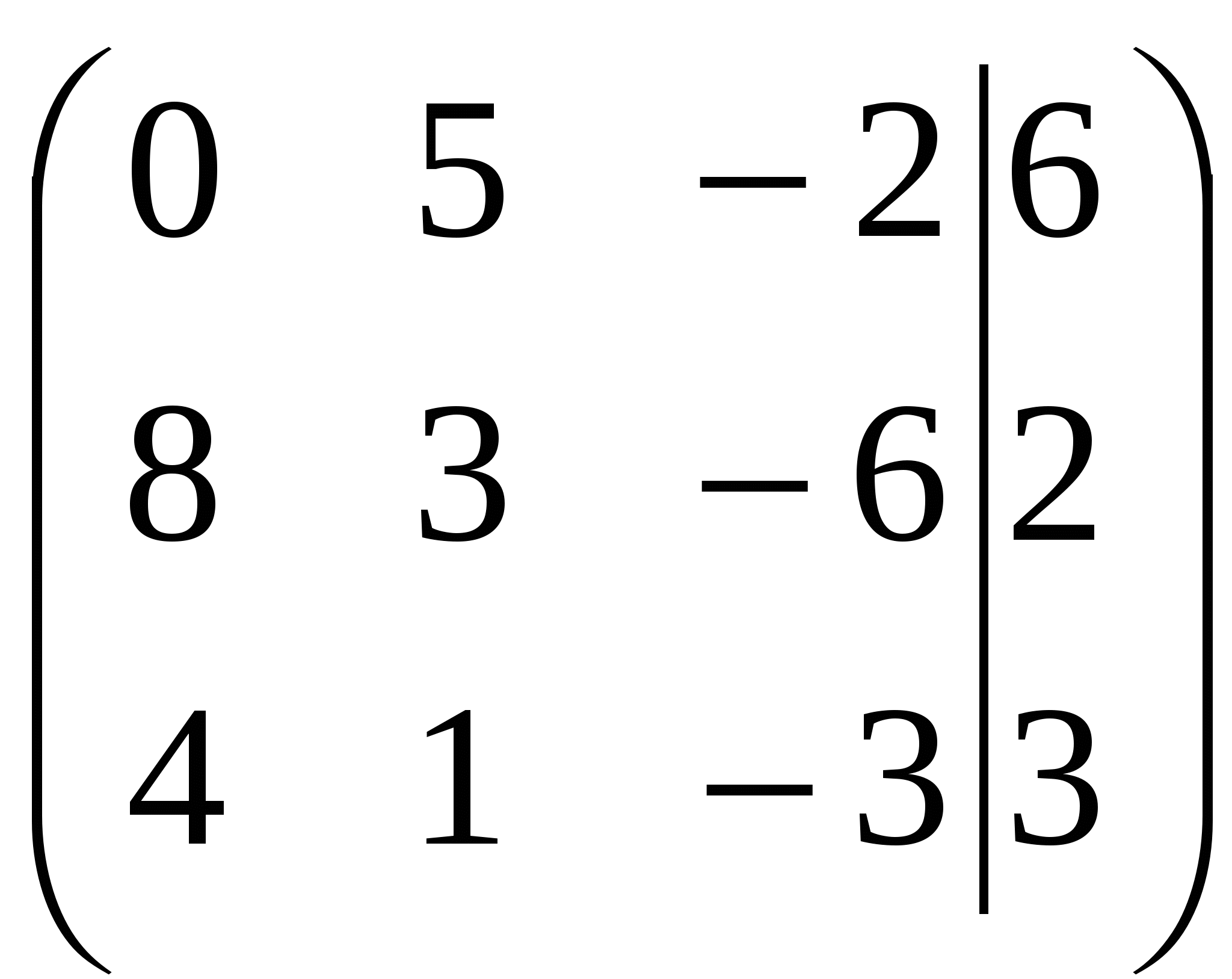

;

5. Умножим третью строку на :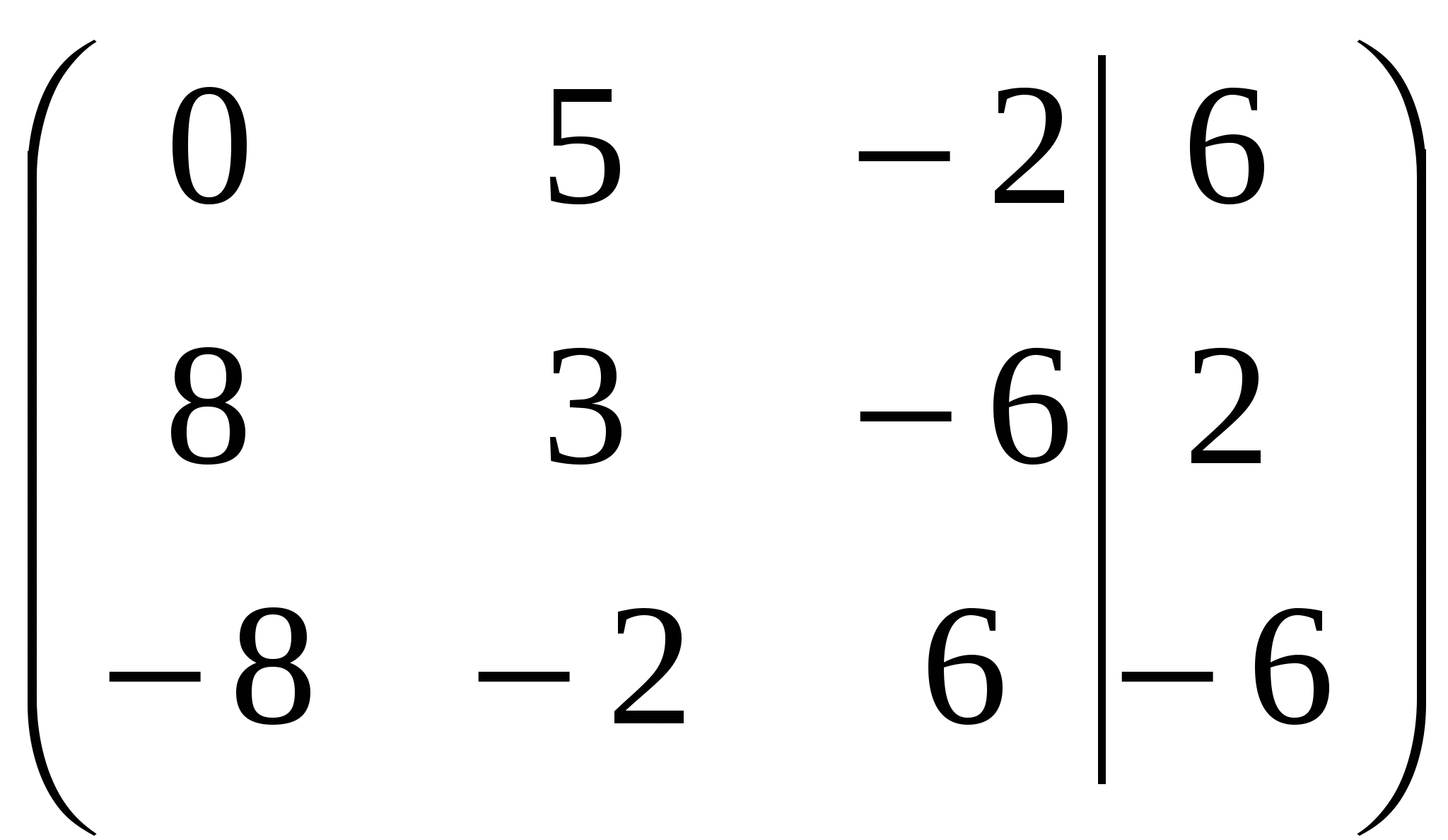

;

6. Прибавим третью строку ко второй строке: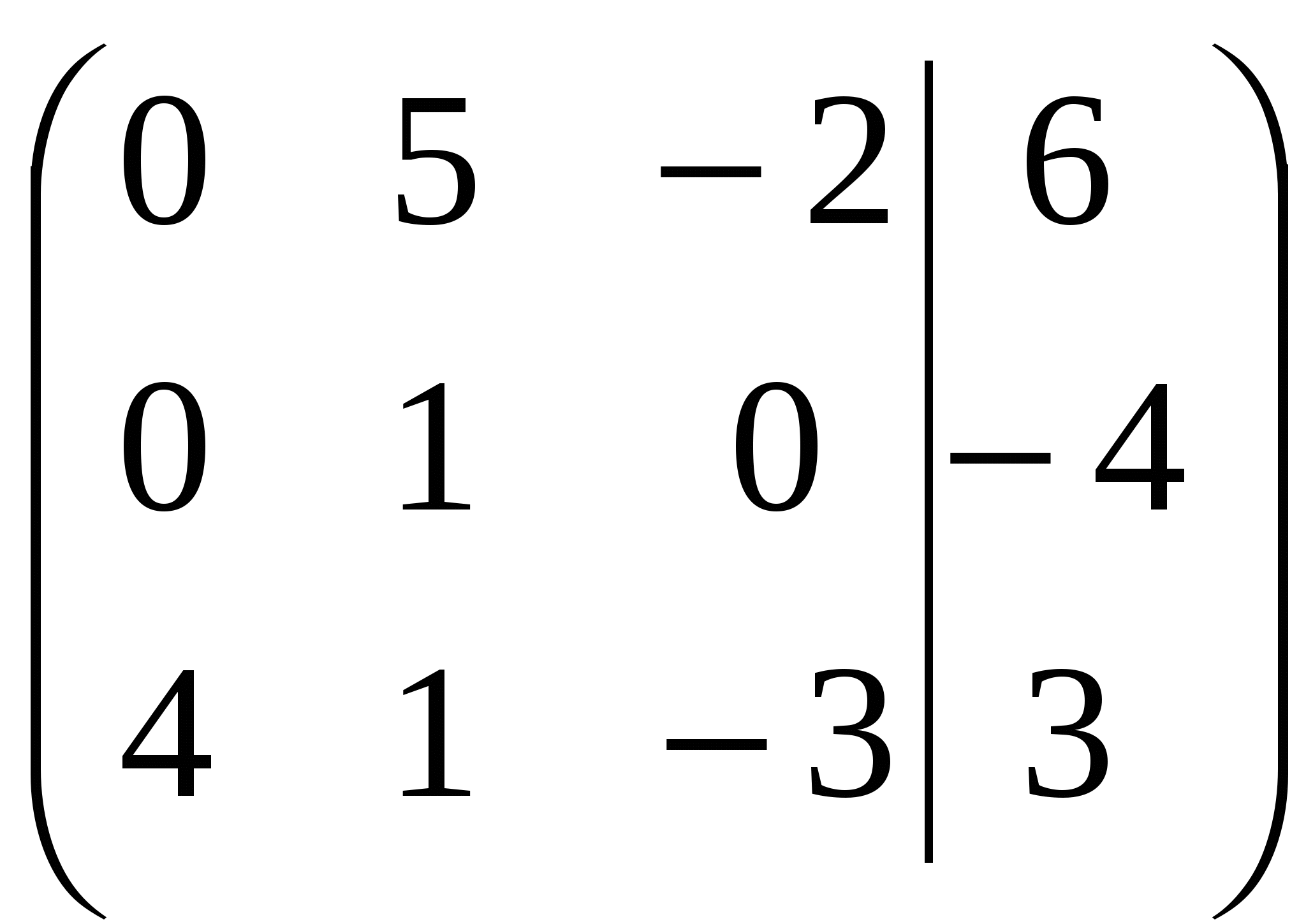

;
7. Умножим вторую строку на :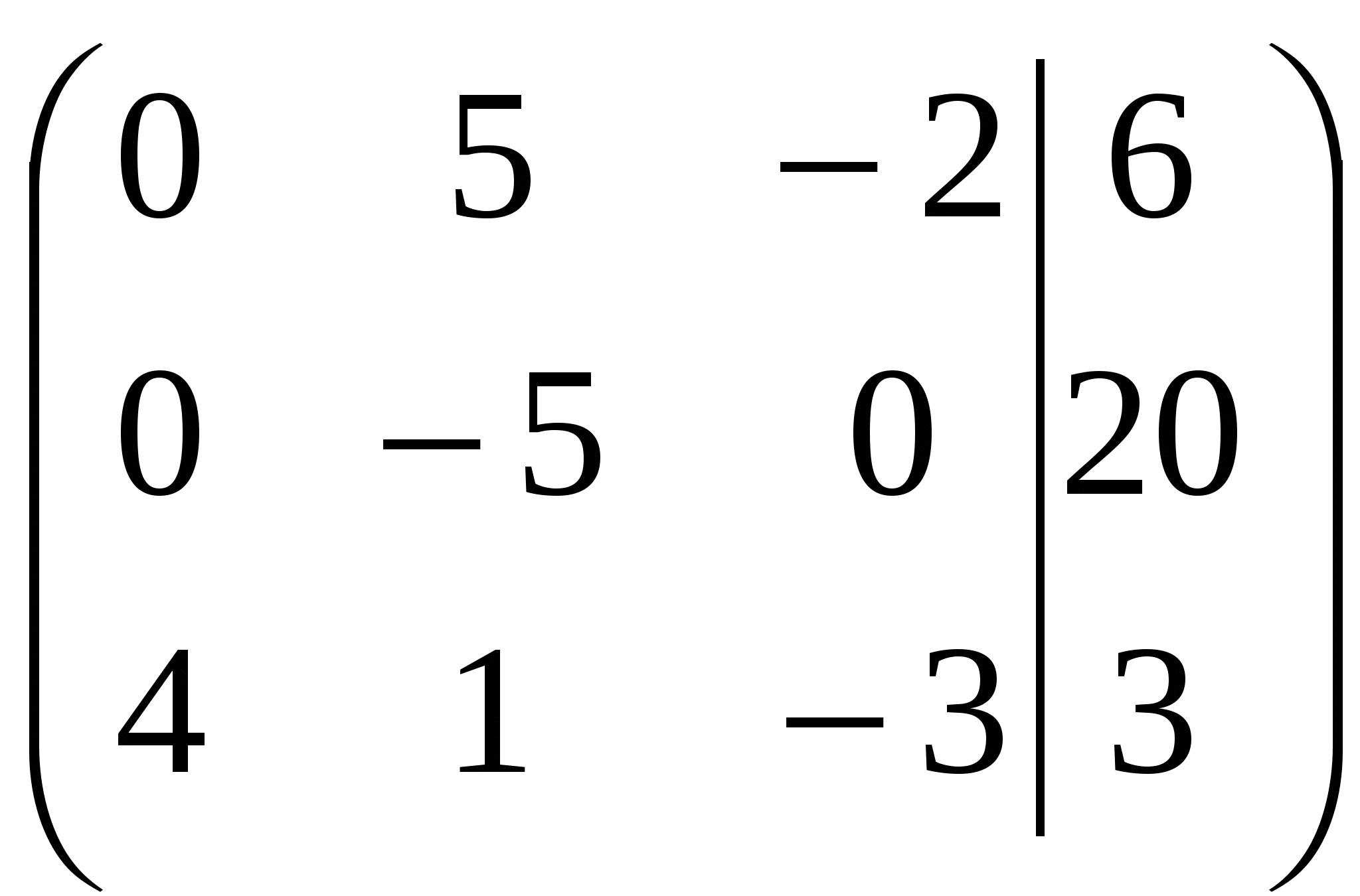
;
8. Прибавим вторую строку к первой строке: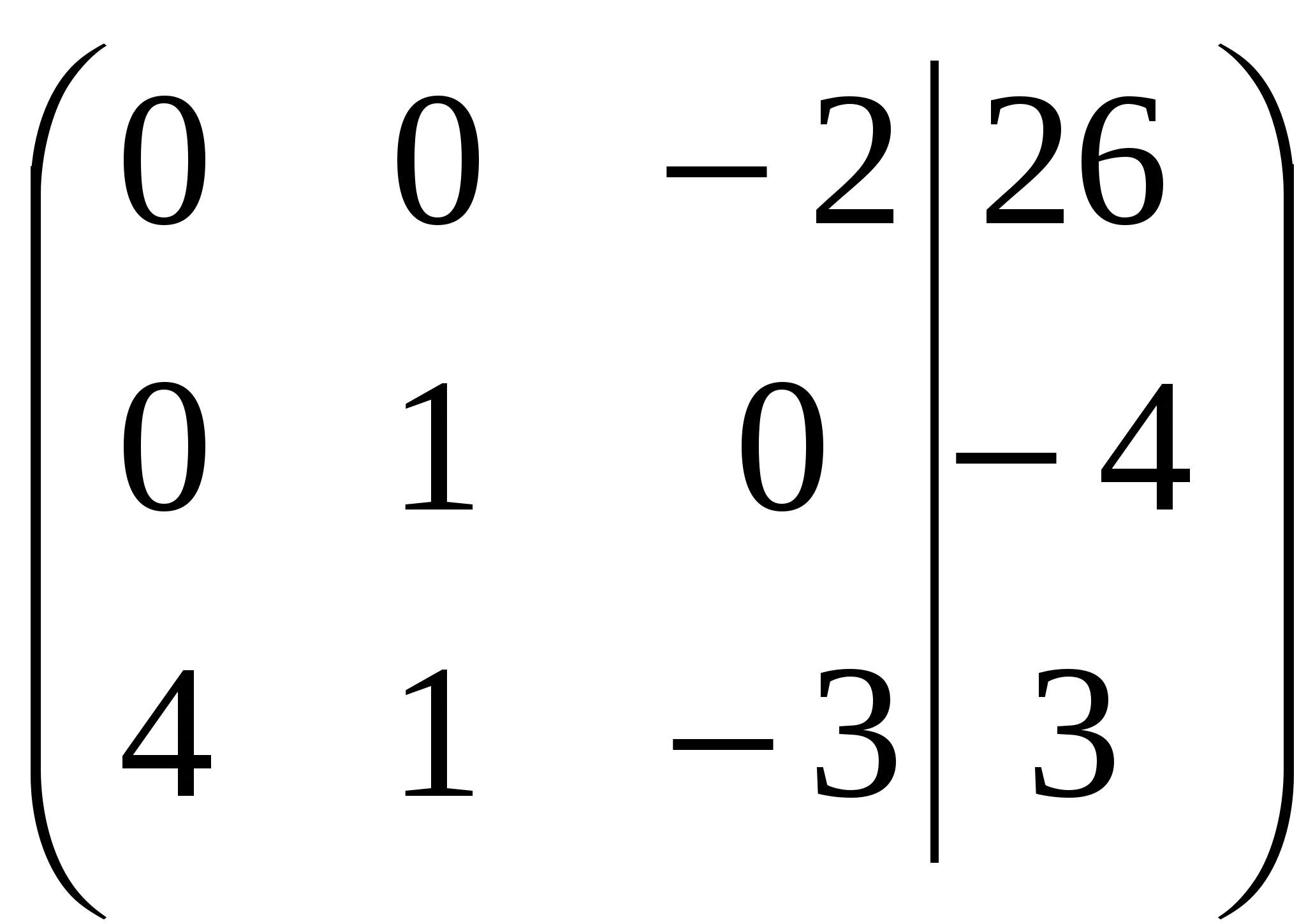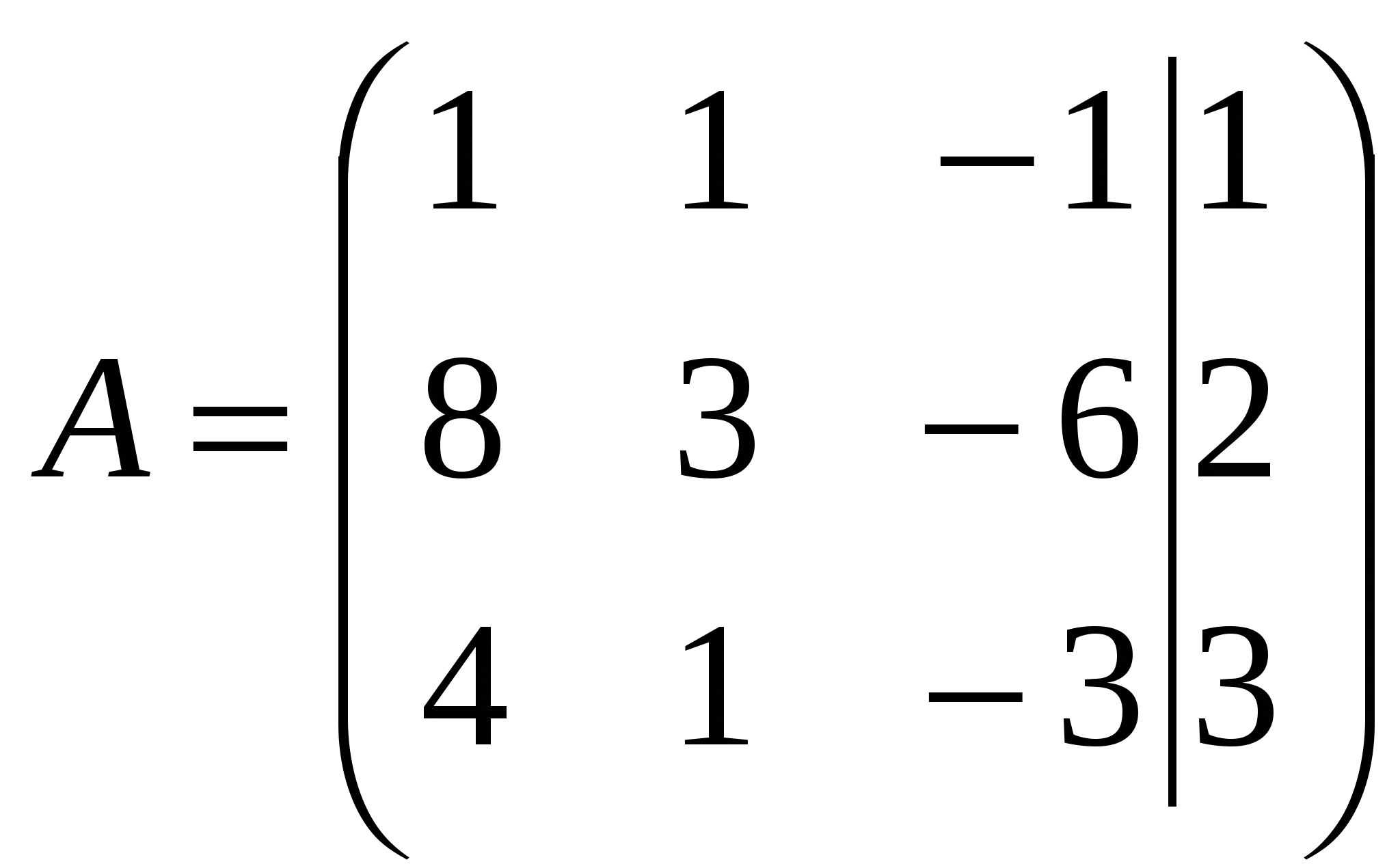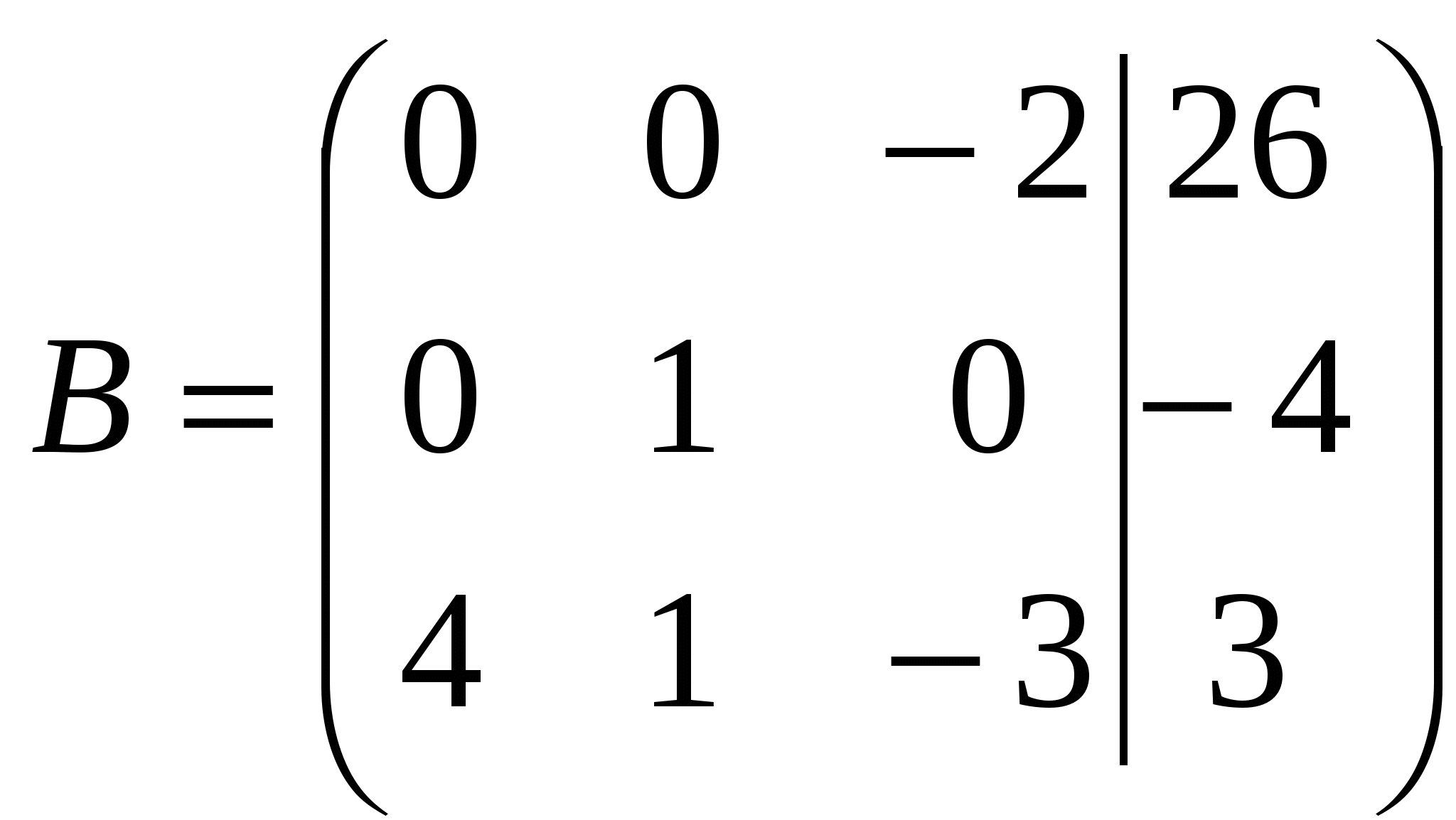
;
;;

Так как , то по теореме Кронекера-Капелли система является совместной.

Система является определённой, так как имеет одно решение.
1) Метод Гаусса
Запишем исходную систему в виде матрицы :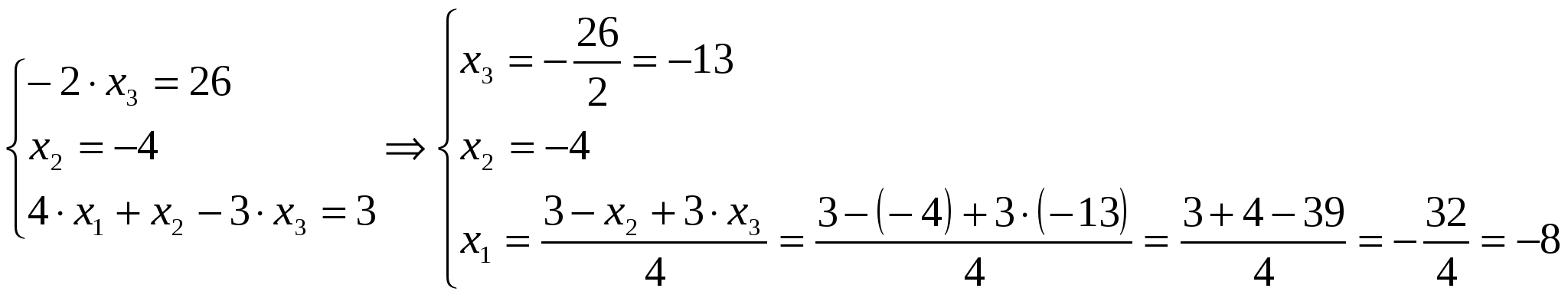


Проверка: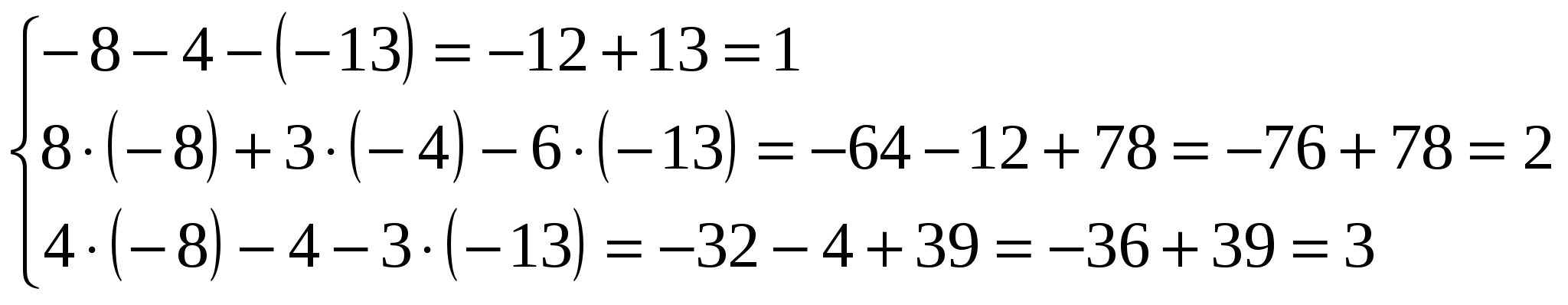


2) Матричный метод.

1. Вычислим определитель матрицы.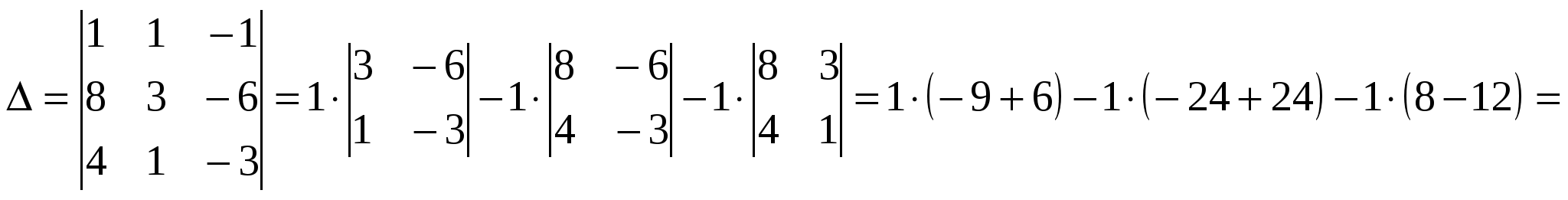



. Следовательно, обратная матрица существует.
2.Найдём алгебраические дополнения матрицы.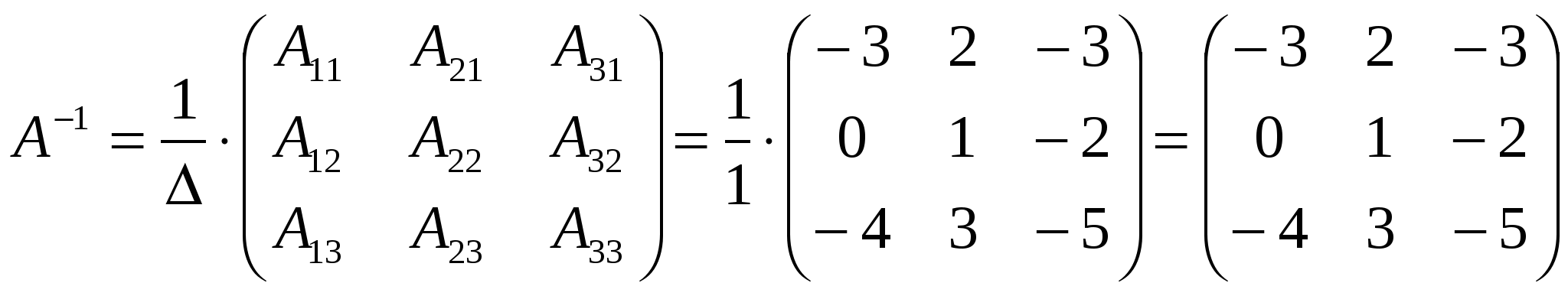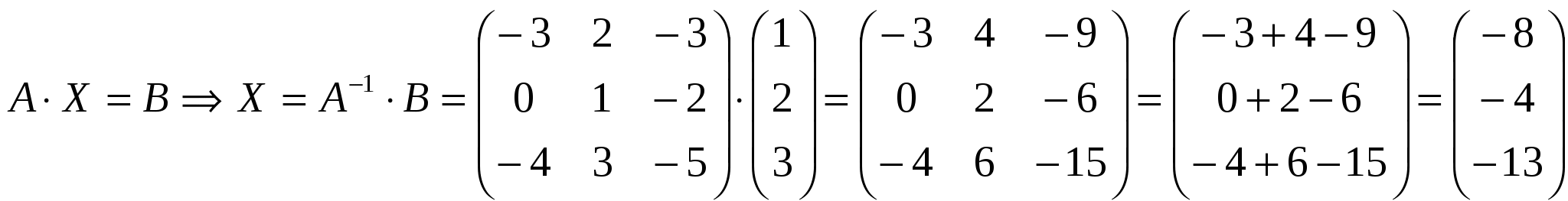

;

;

;

;

;

;

;
;

;

;

.

Следовательно: ,, .
17. Даны координаты вершин пирамиды , , , . Найти 1) длину ребра ; 2) Угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объём пирамиды; 6) уравнение прямой ; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань . Сделать чертёж.

, , , .

Решение:

; ;

;

1) ;

2)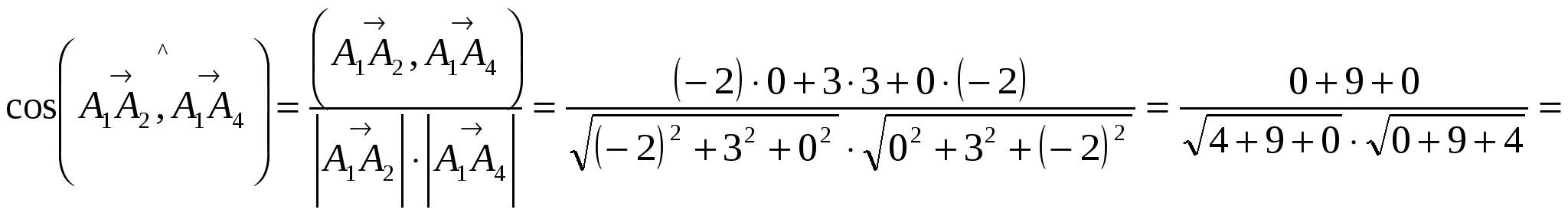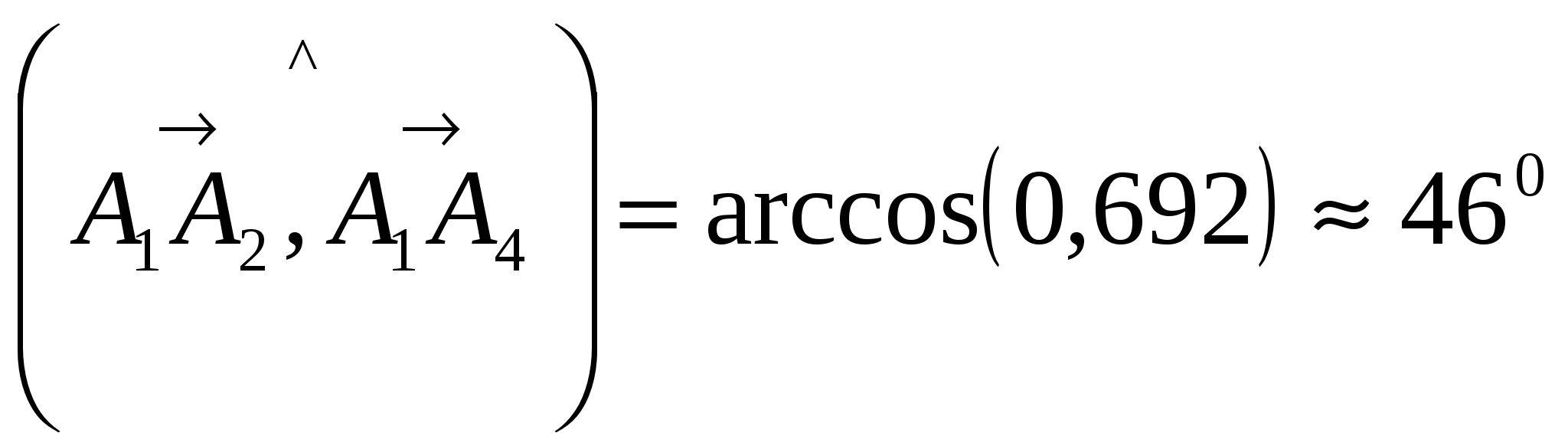

; ;

3)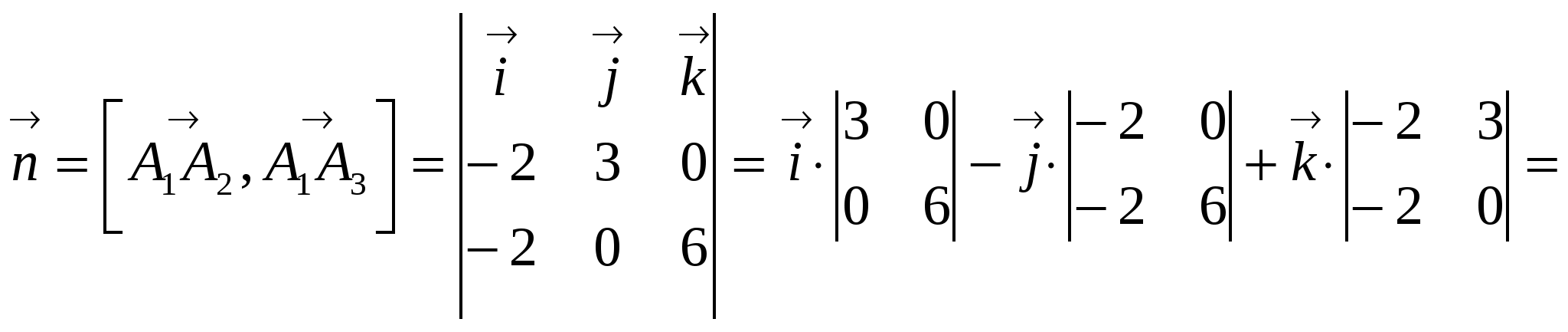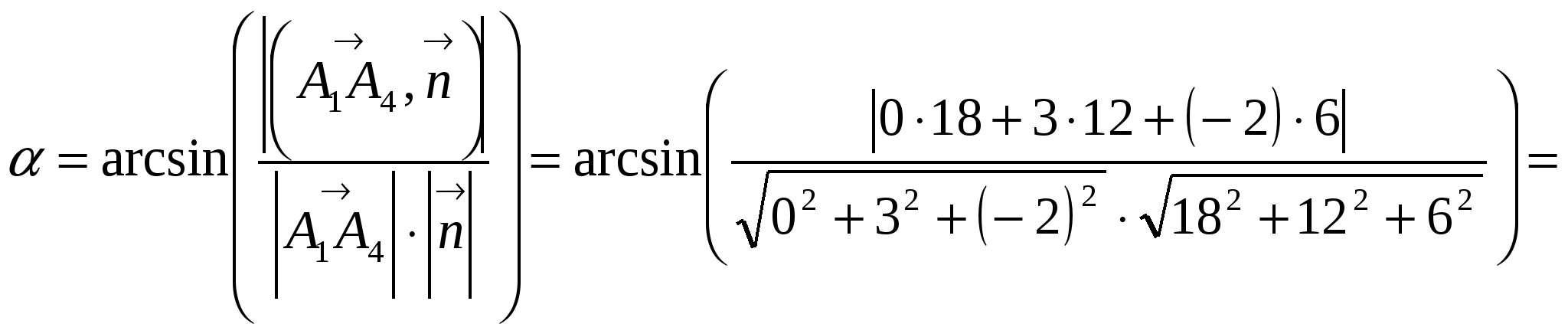

;;







;
4) ;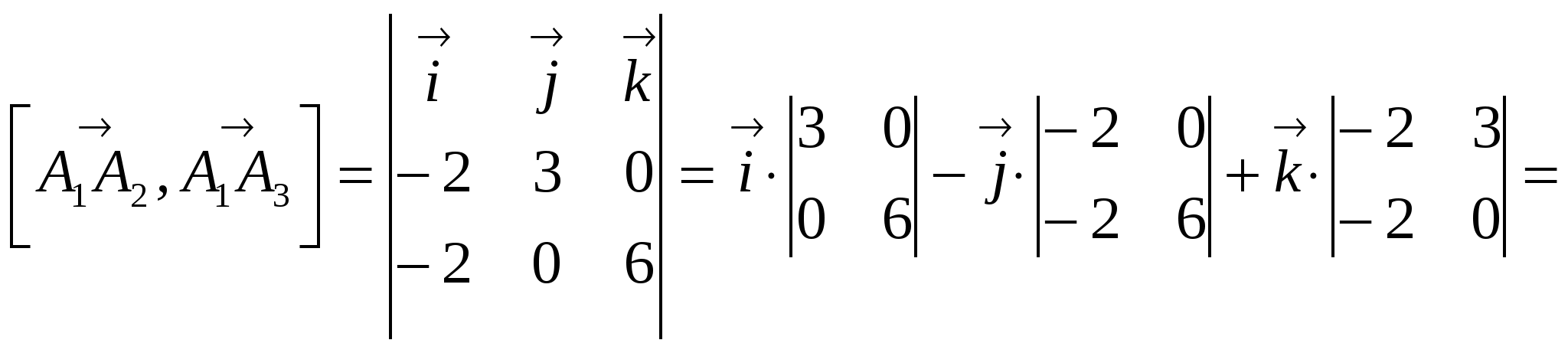

;

; ;

5) ;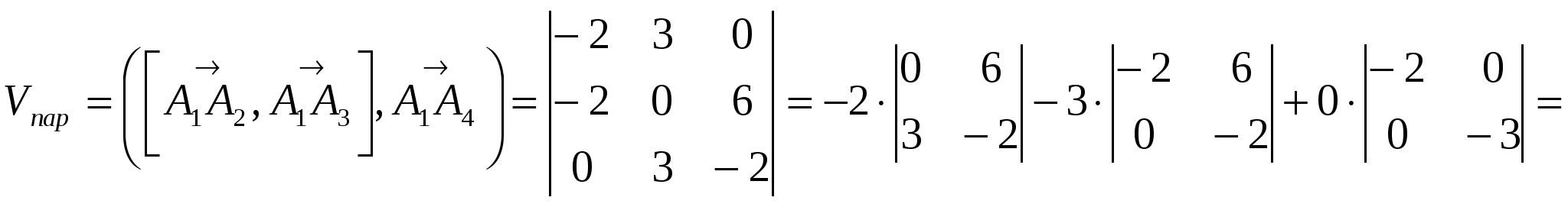



; ;

6) ; ; ;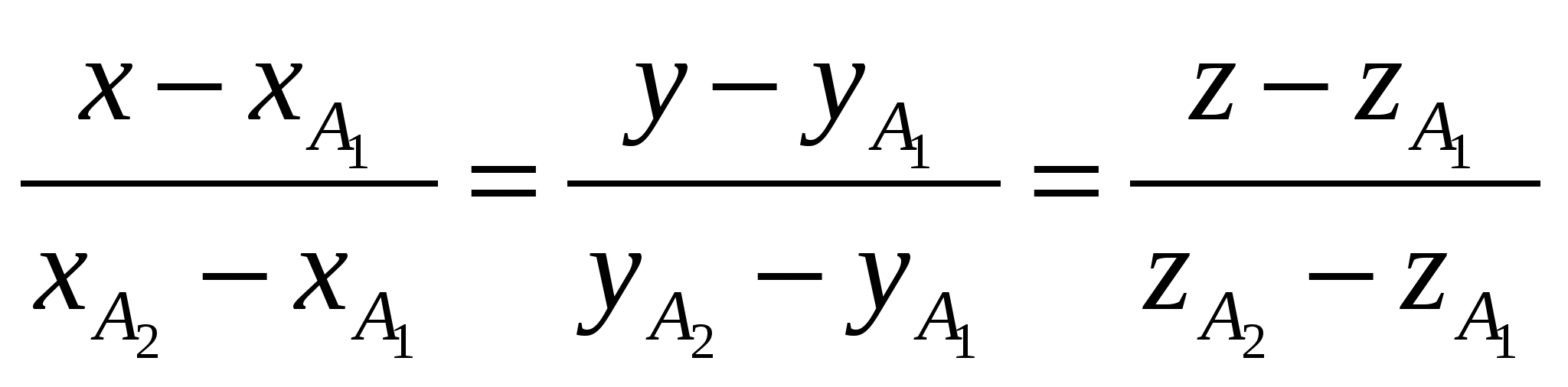
7) Уравнение плоскости, проходящее через три точки, имеет вид: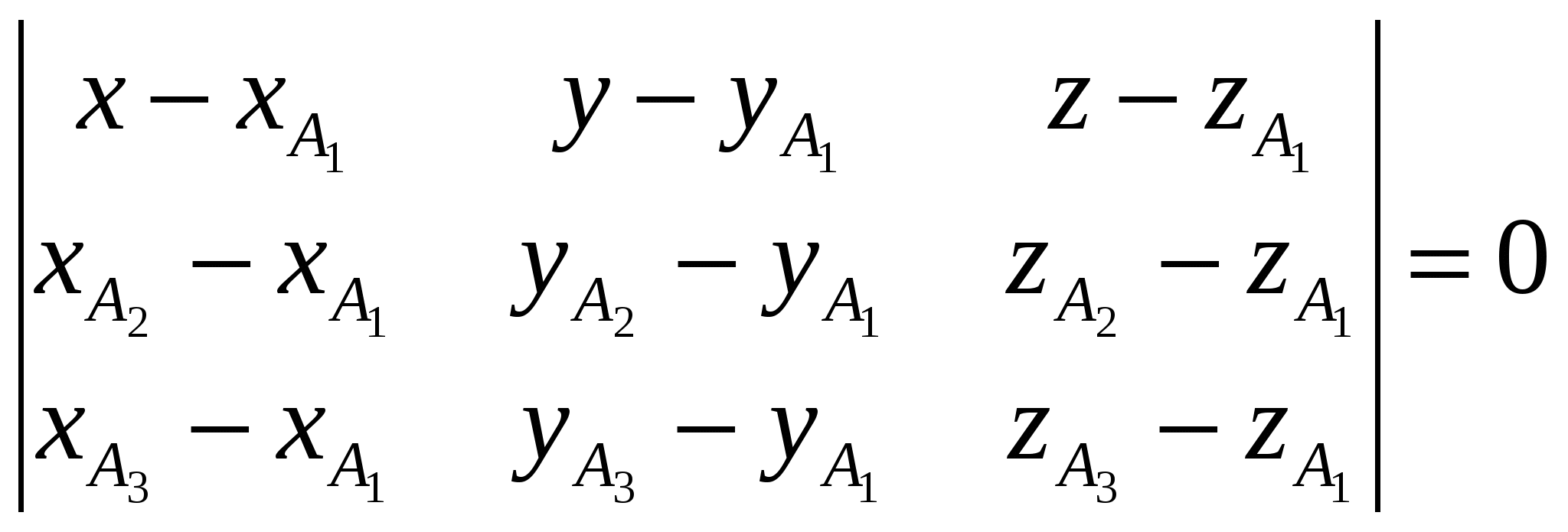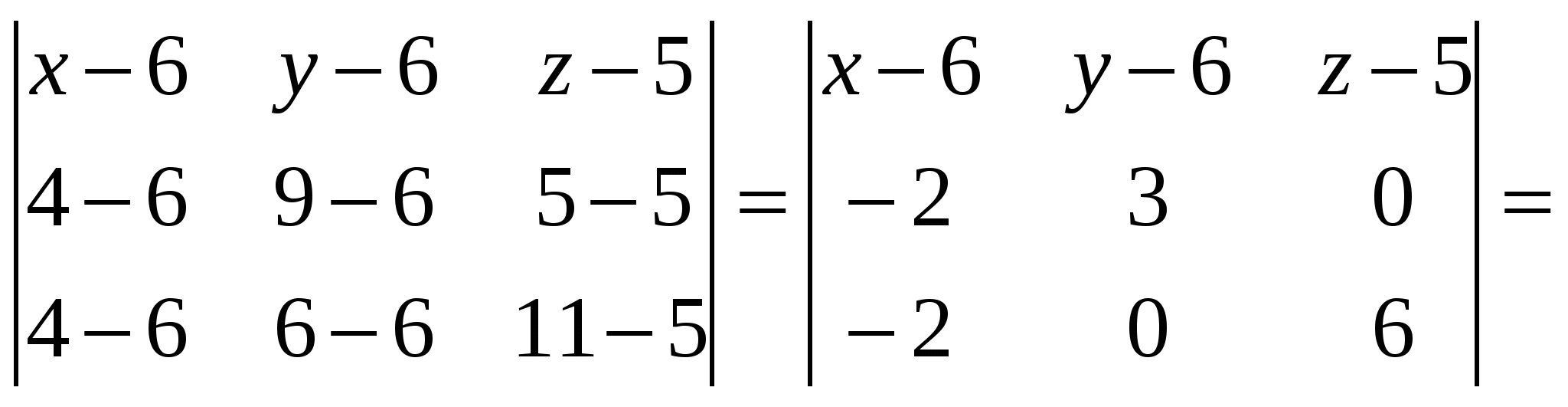

;




; ; ;
8) Уравнения высоты 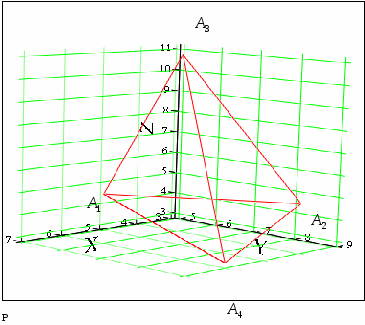, опущенной из вершины  на грань , составим по точке   и направляющему вектору :;


27. Линия задана уравнением в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от до, придавая через промежуток;

2) найти уравнение в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;

3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.


1) ;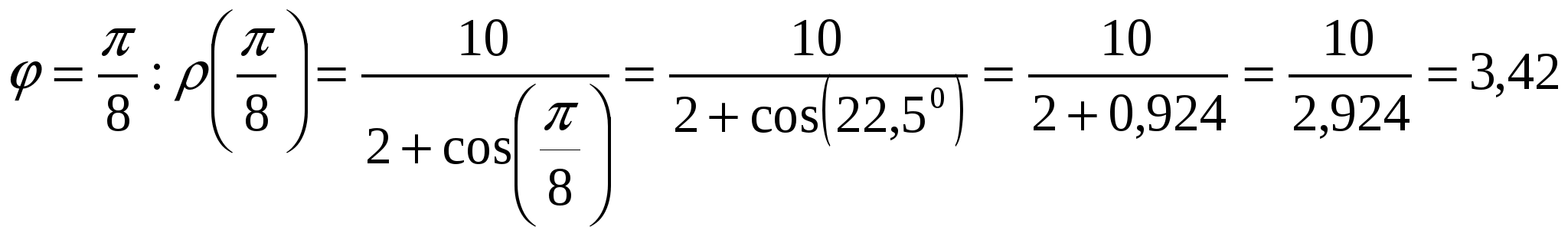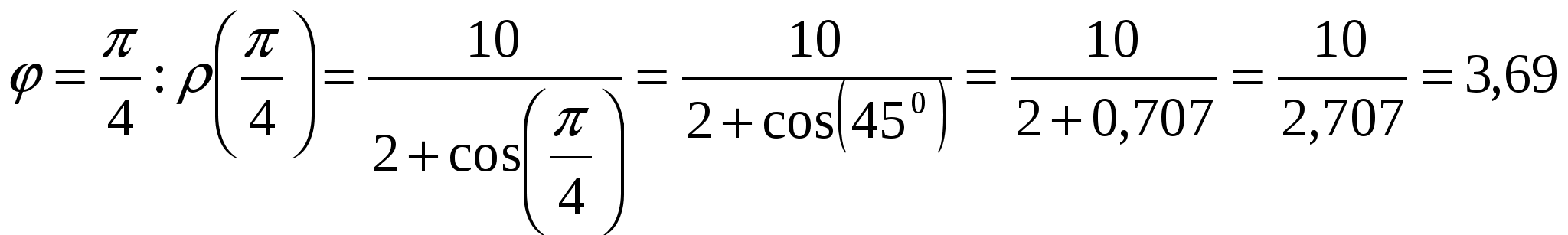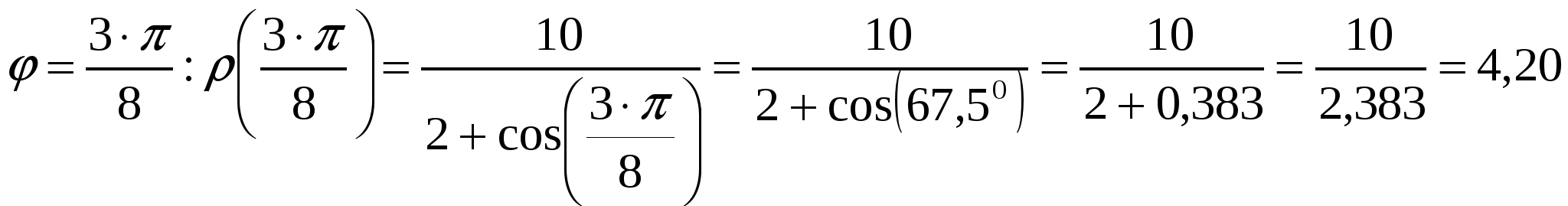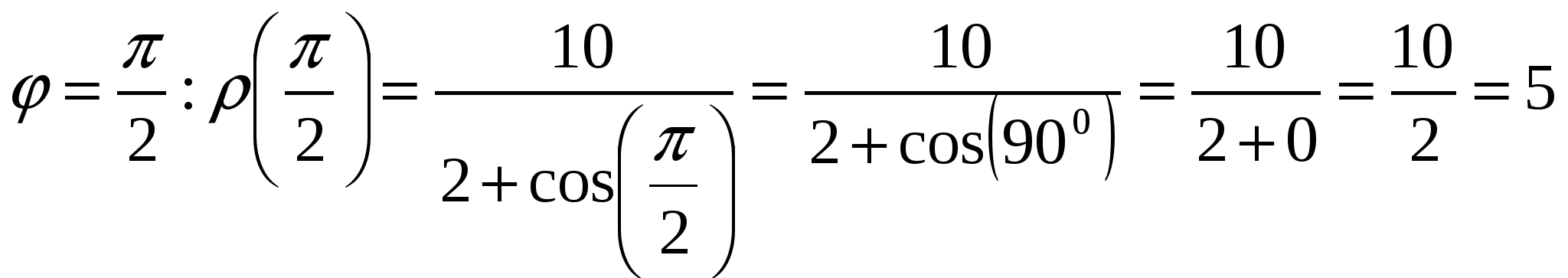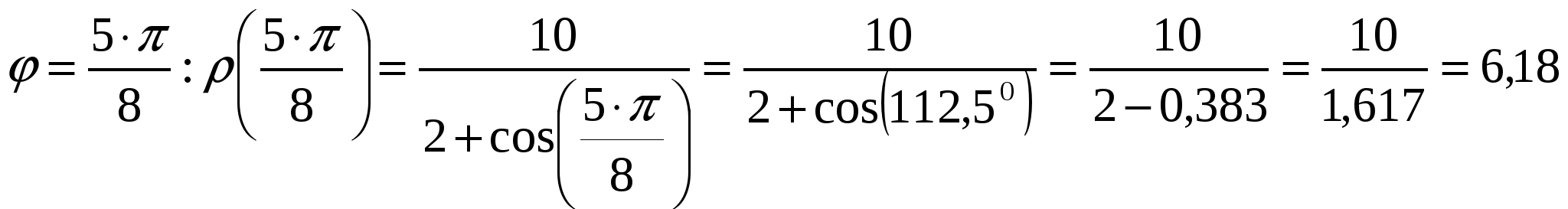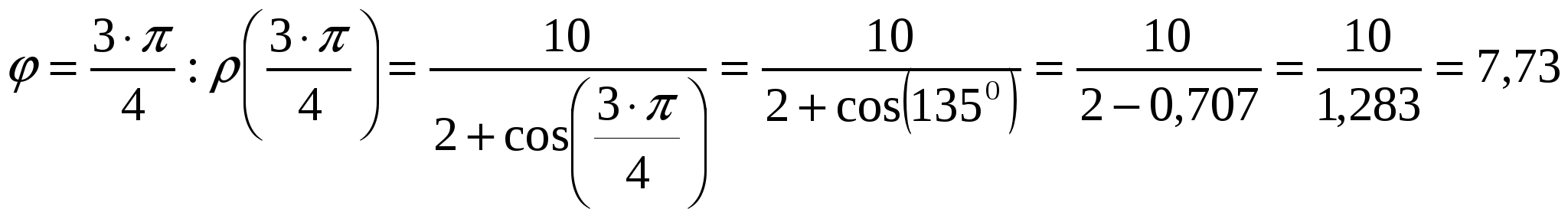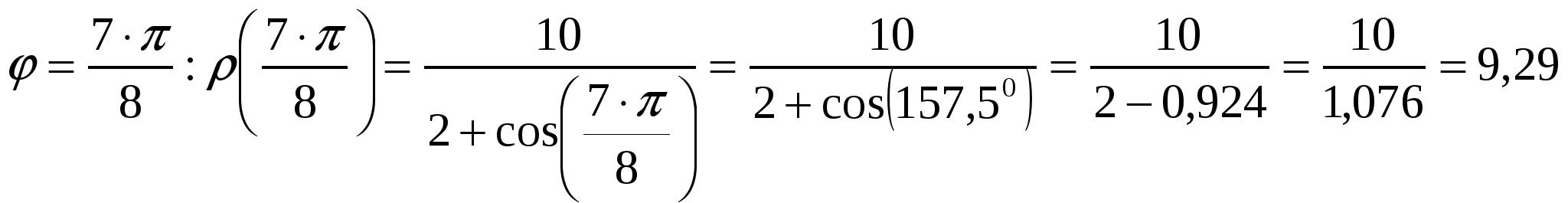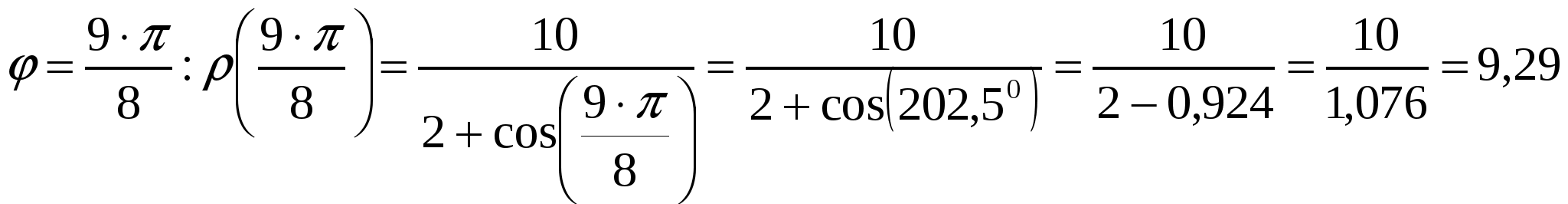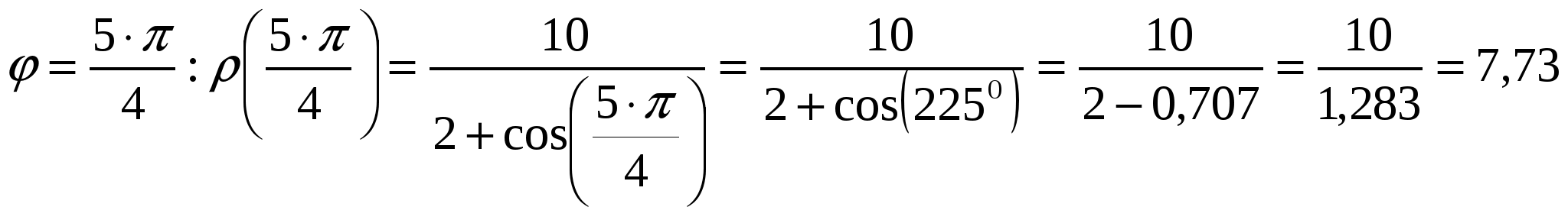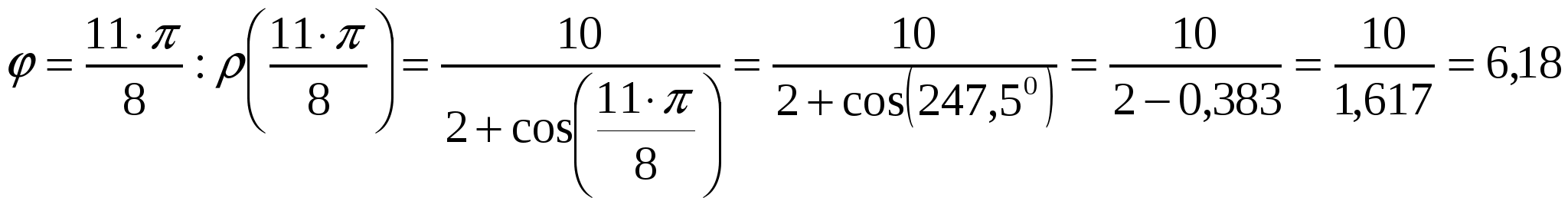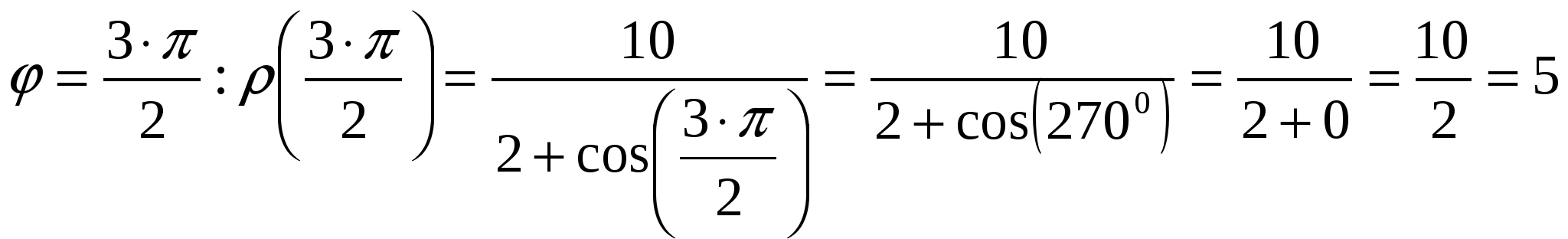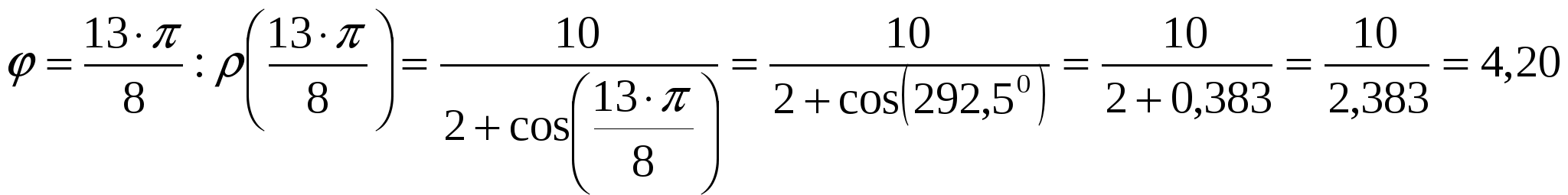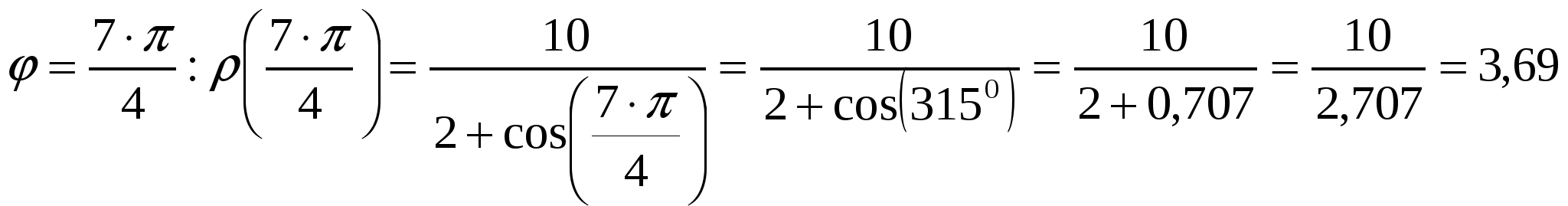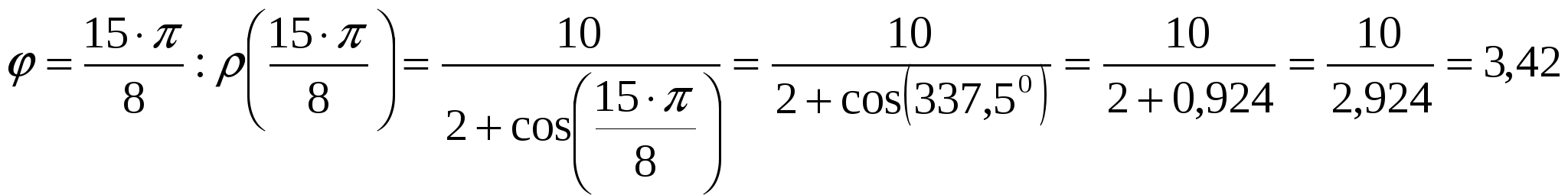

;

;

;

;

;

;

;

;
;

;
;

;

;
;

;

;

2) ; ;

;

;

;

;
;
;
;
;
;
;
; ; ;
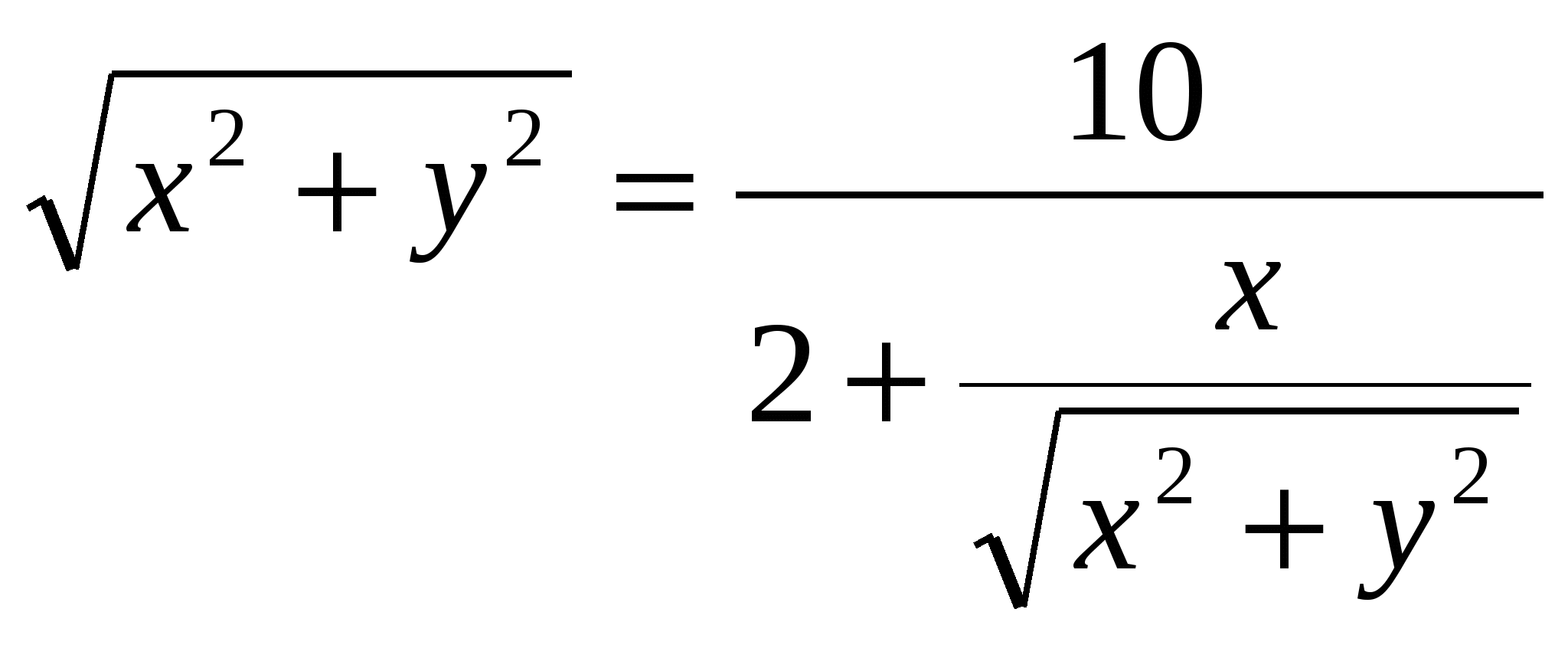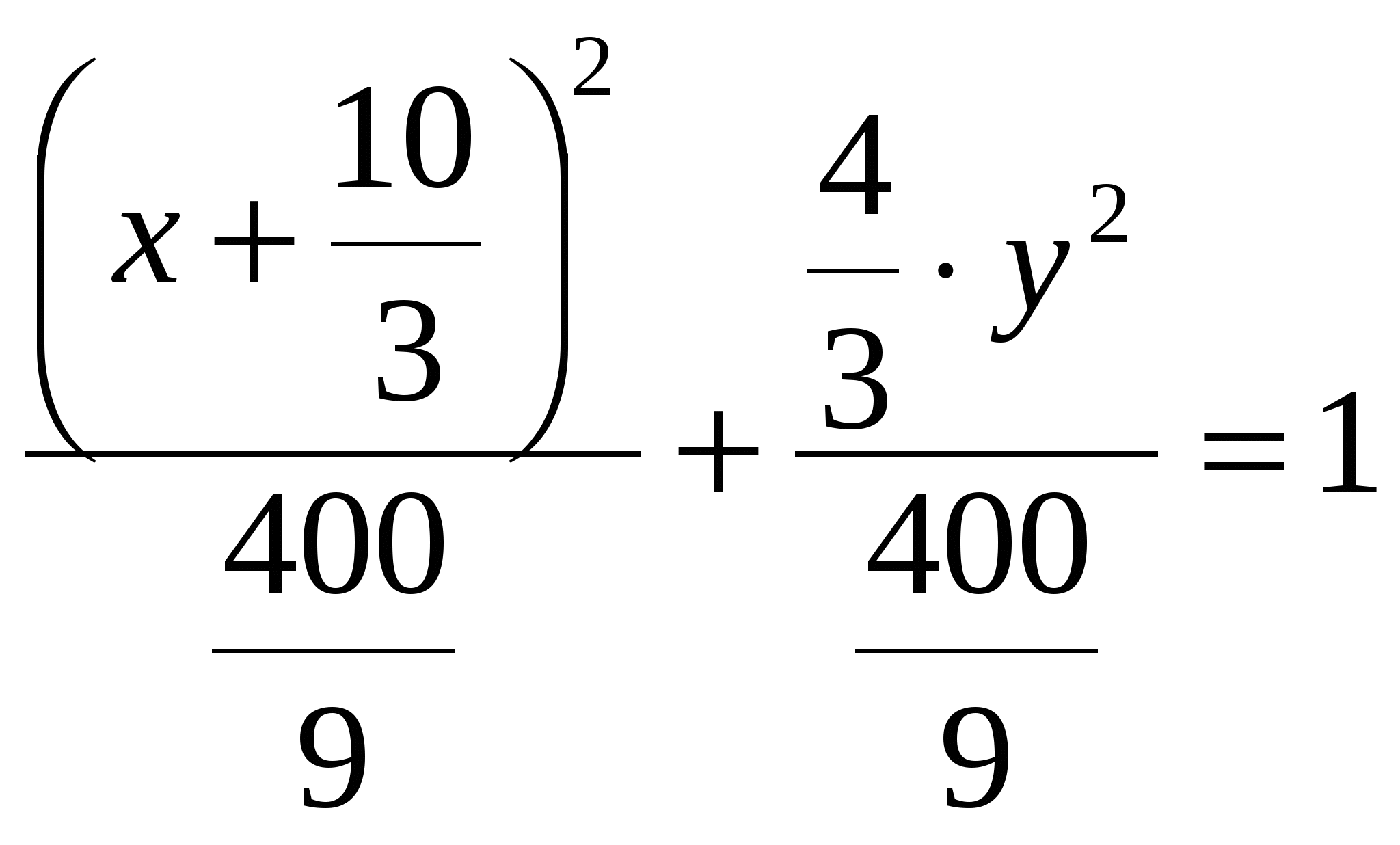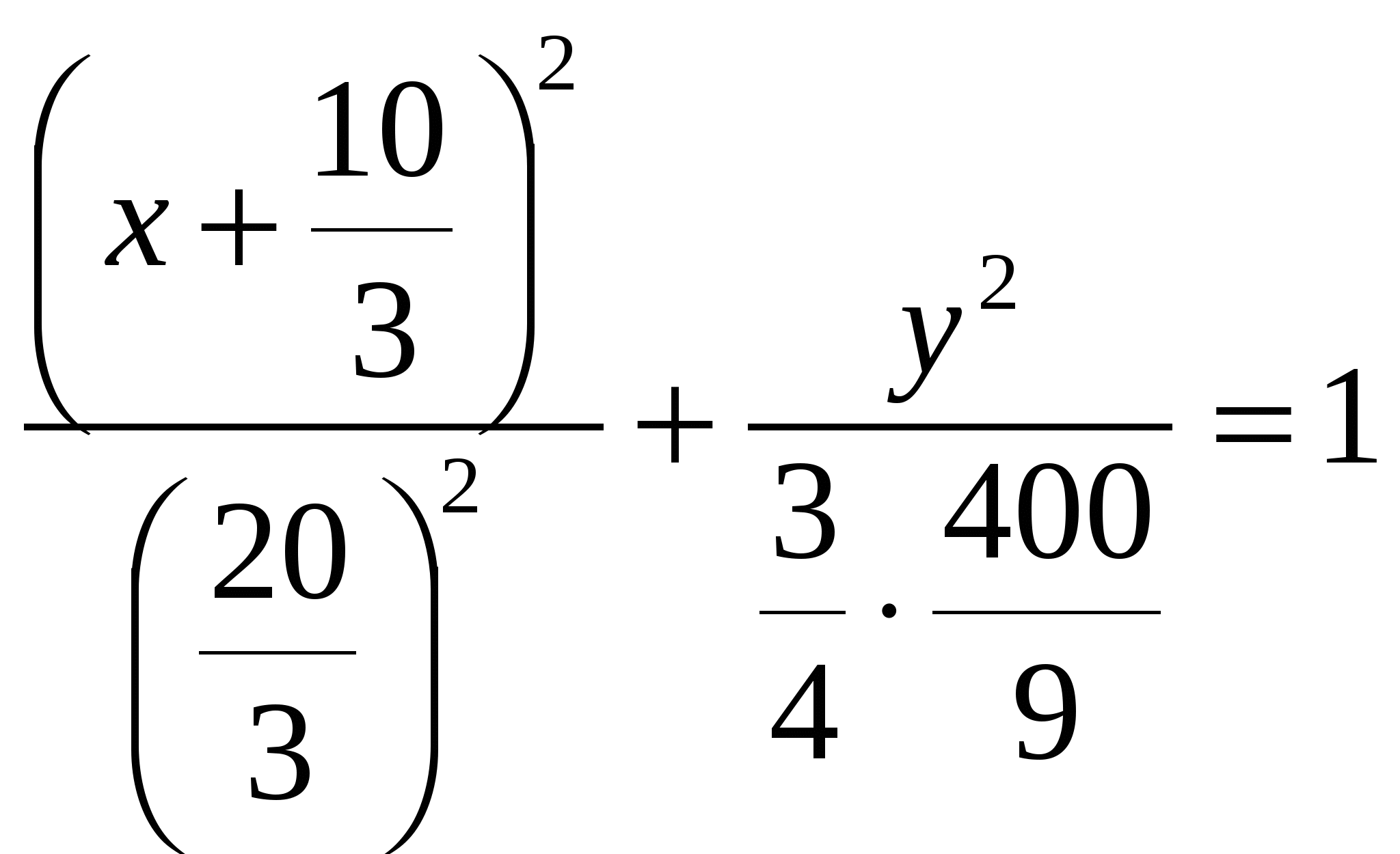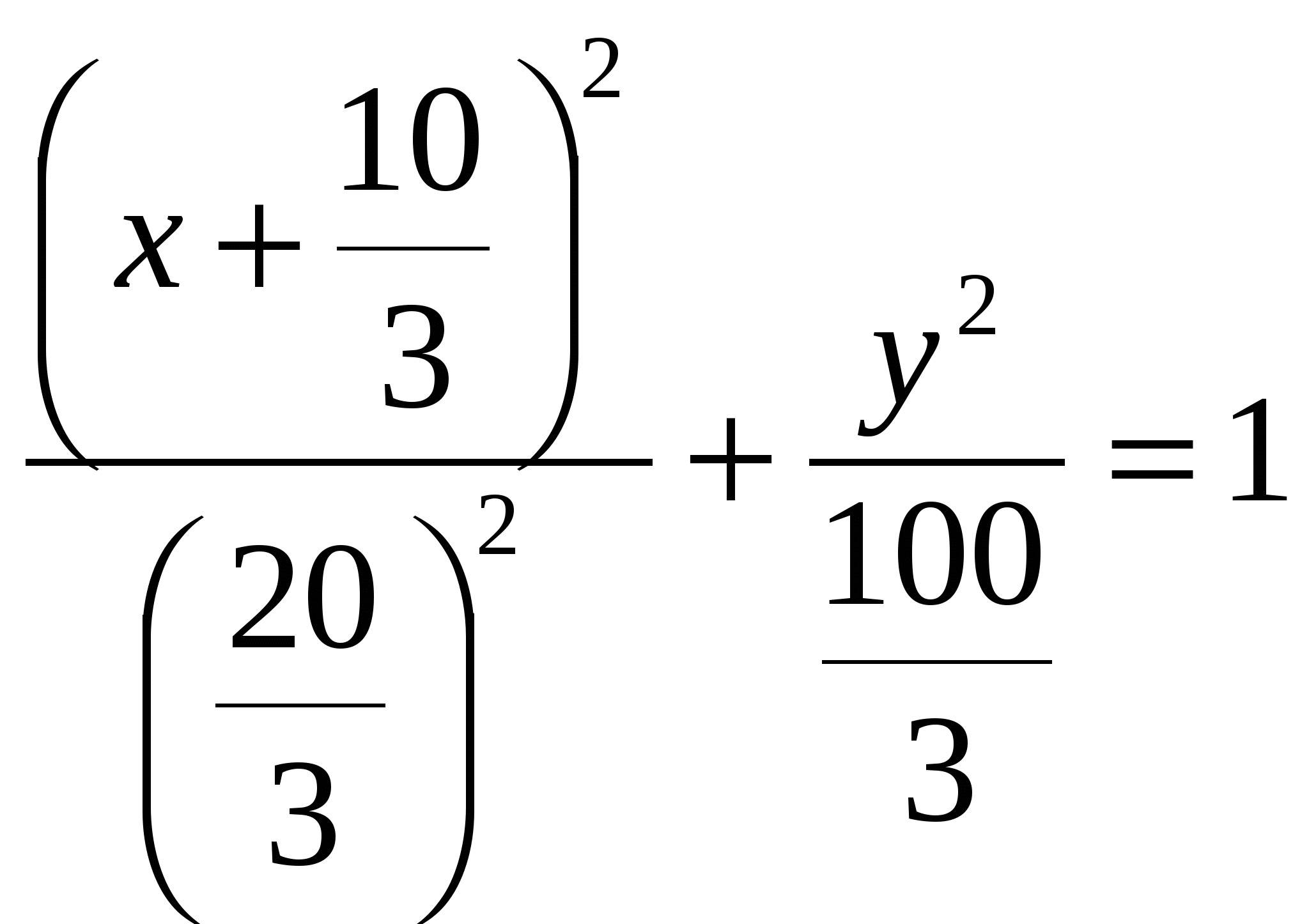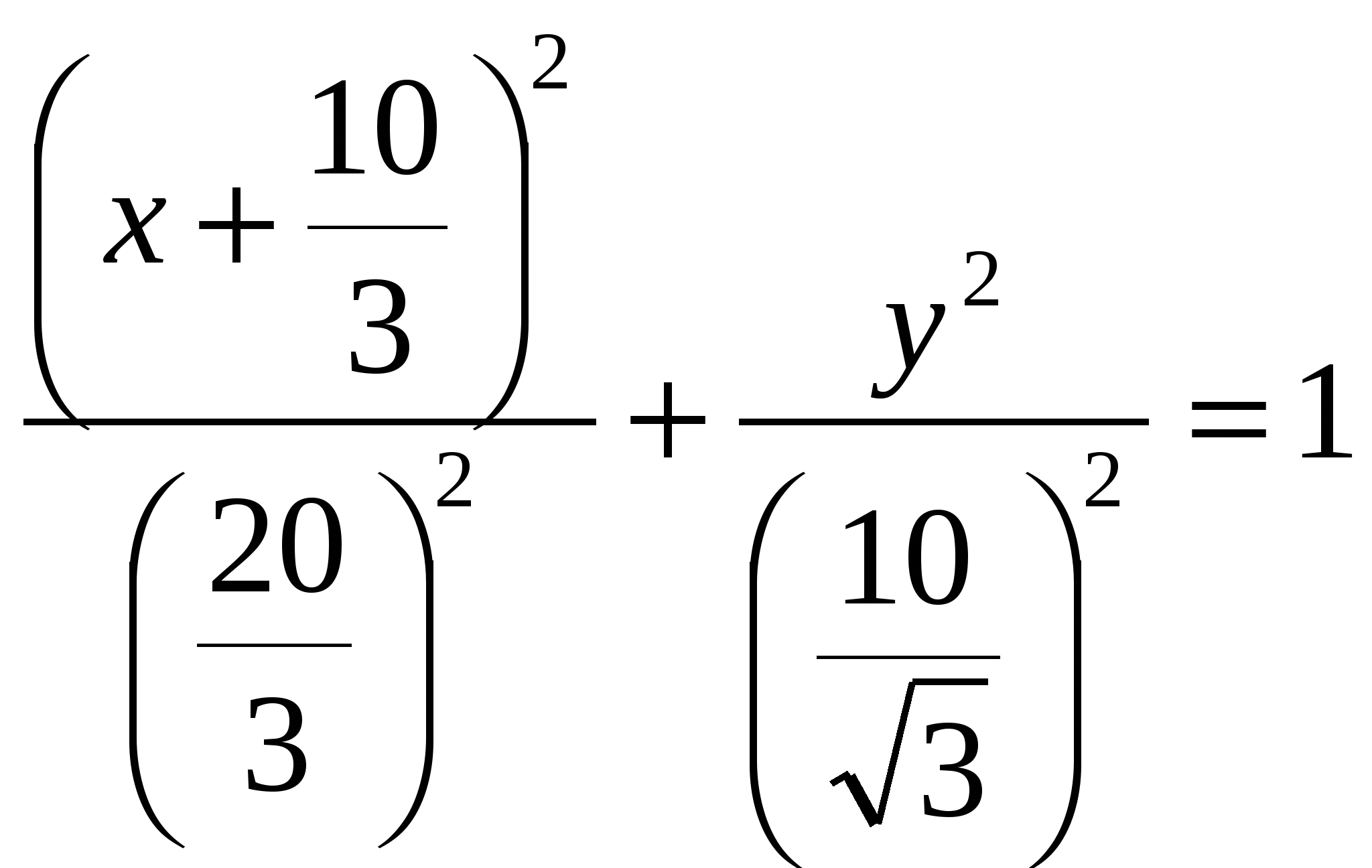3) 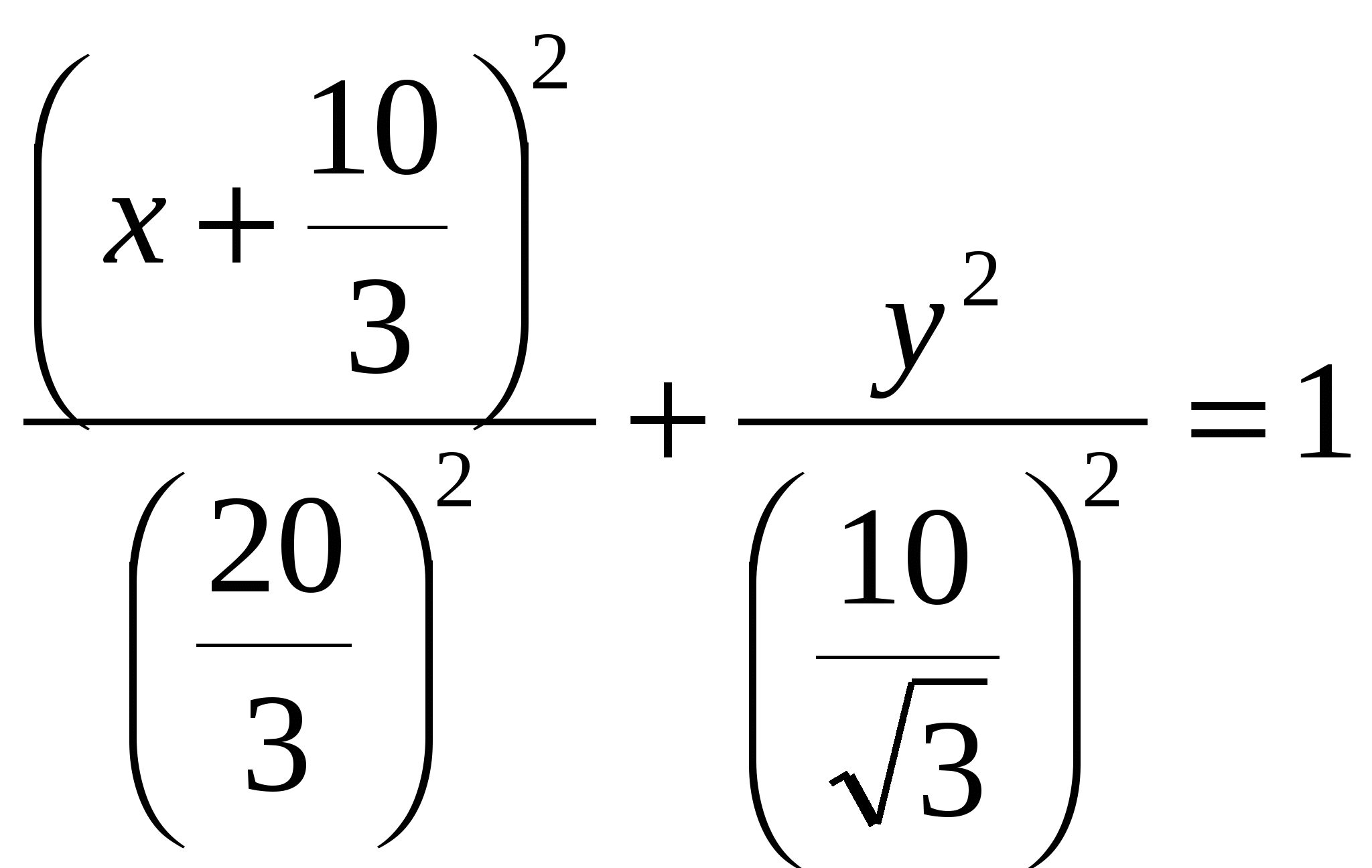- каноническое уравнение эллипса, где - большая полуось,
- малая полуось.

37. Найти пределы функции, не пользуясь правилом Лопиталя.

а) ;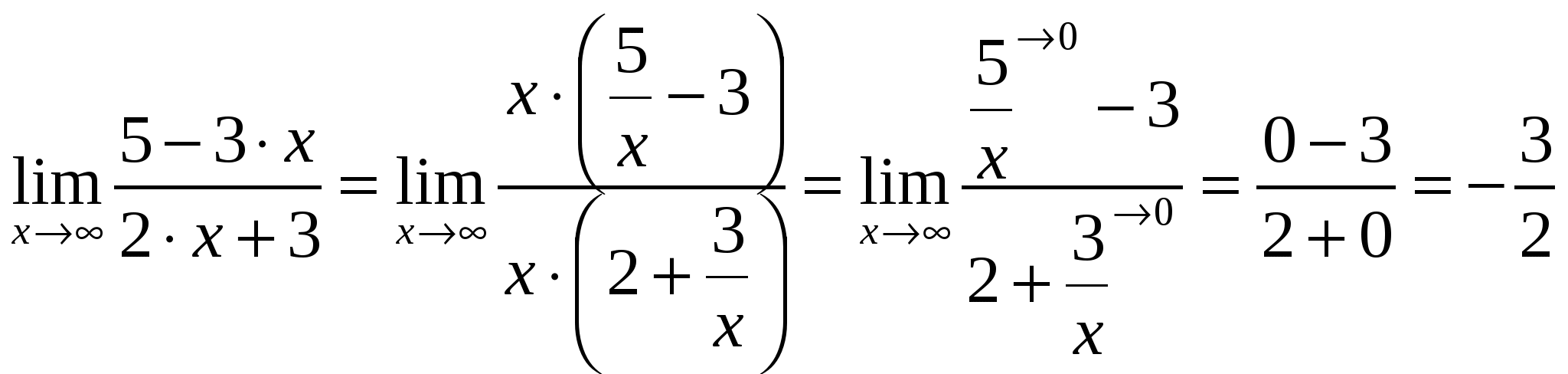

б) ; ; ;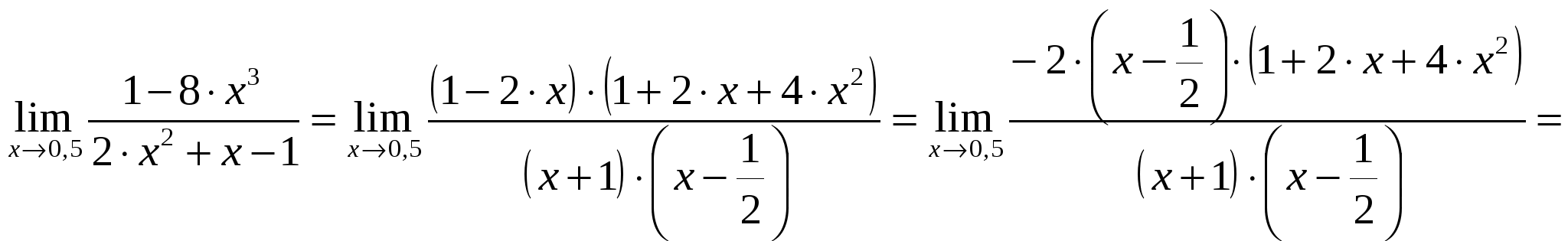
; . Следовательно:

;
в) . Используем свойство эквивалентности:

при : ; . Следовательно:
47. Найти производные д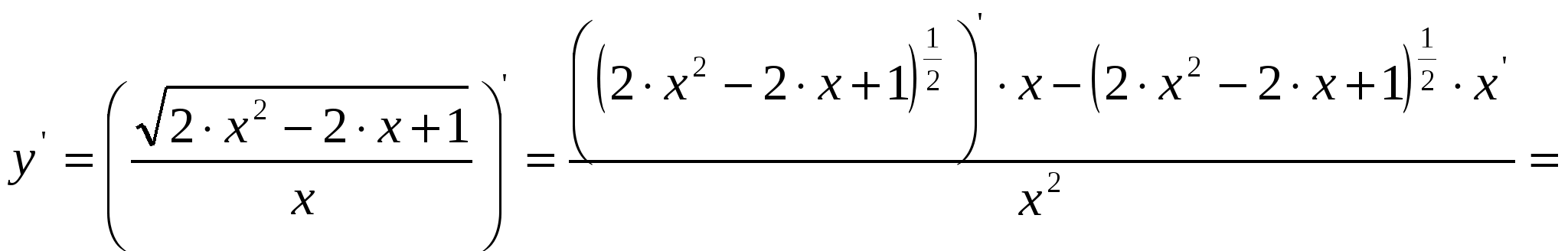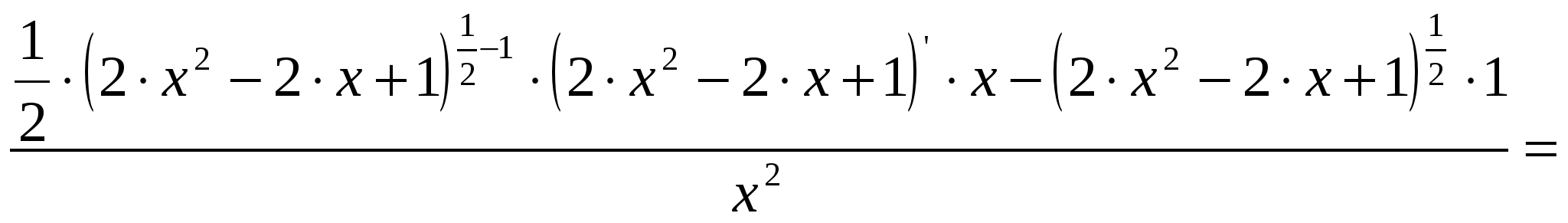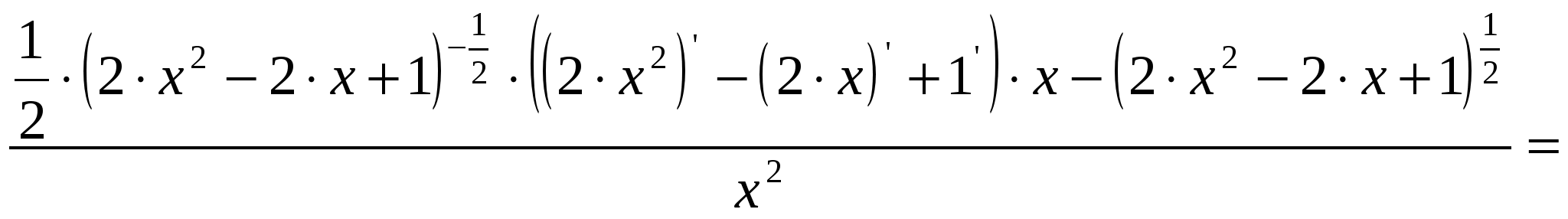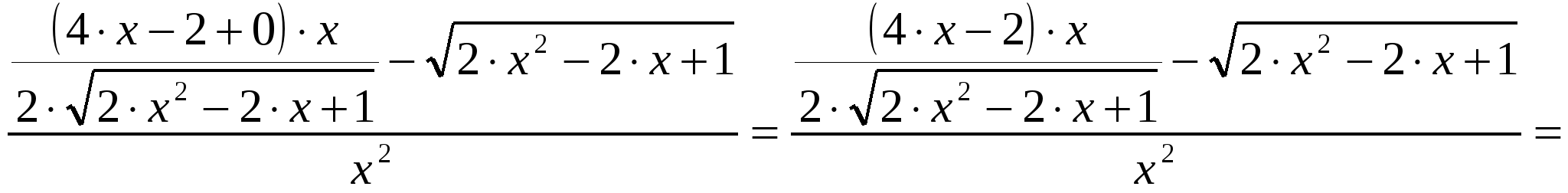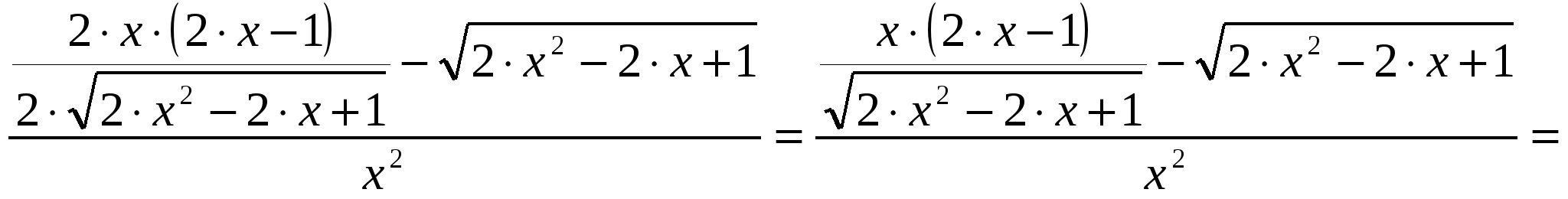анных функций.

а) ;








;
б) ;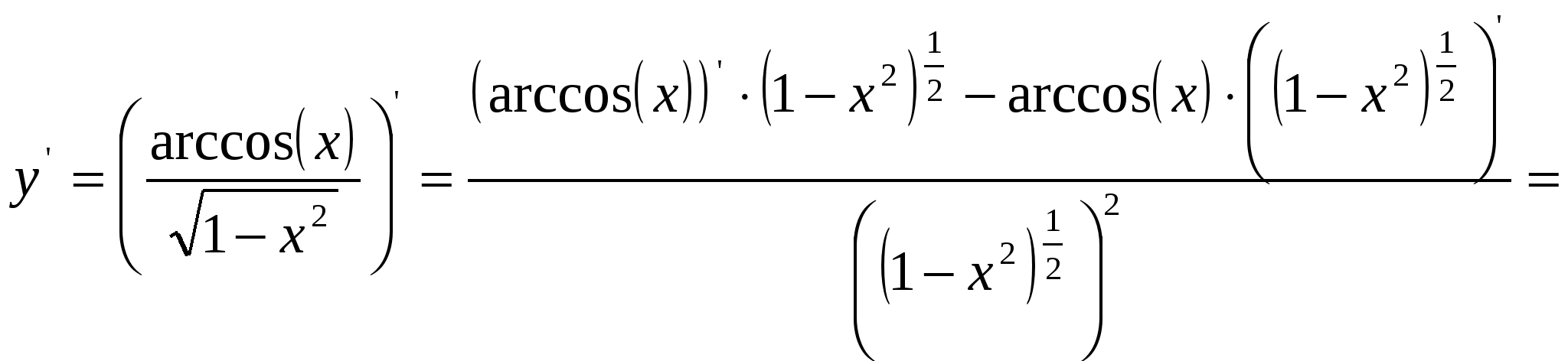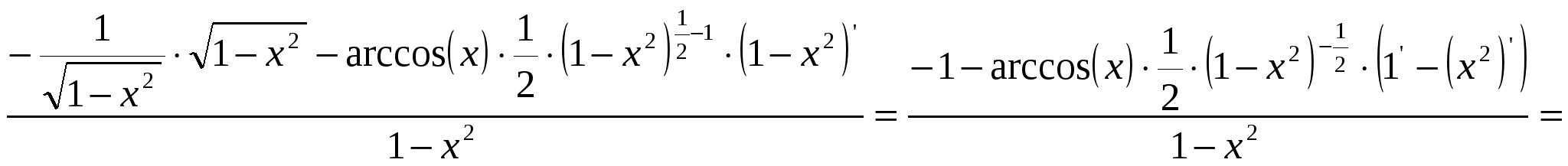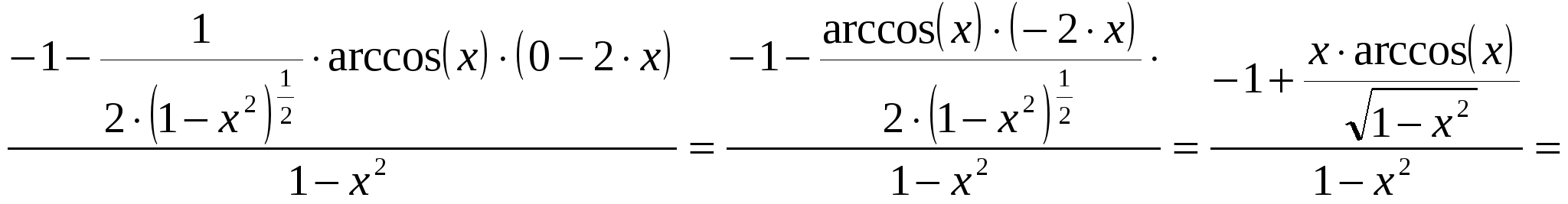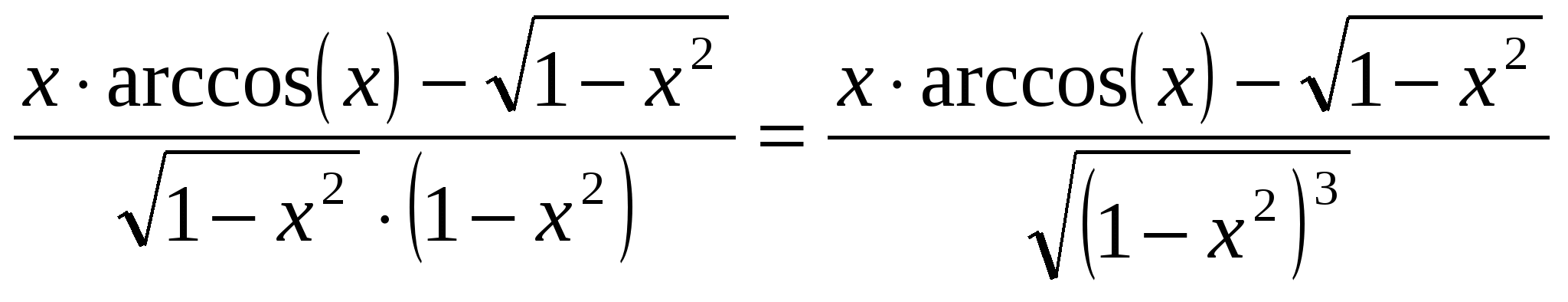



;

в) ;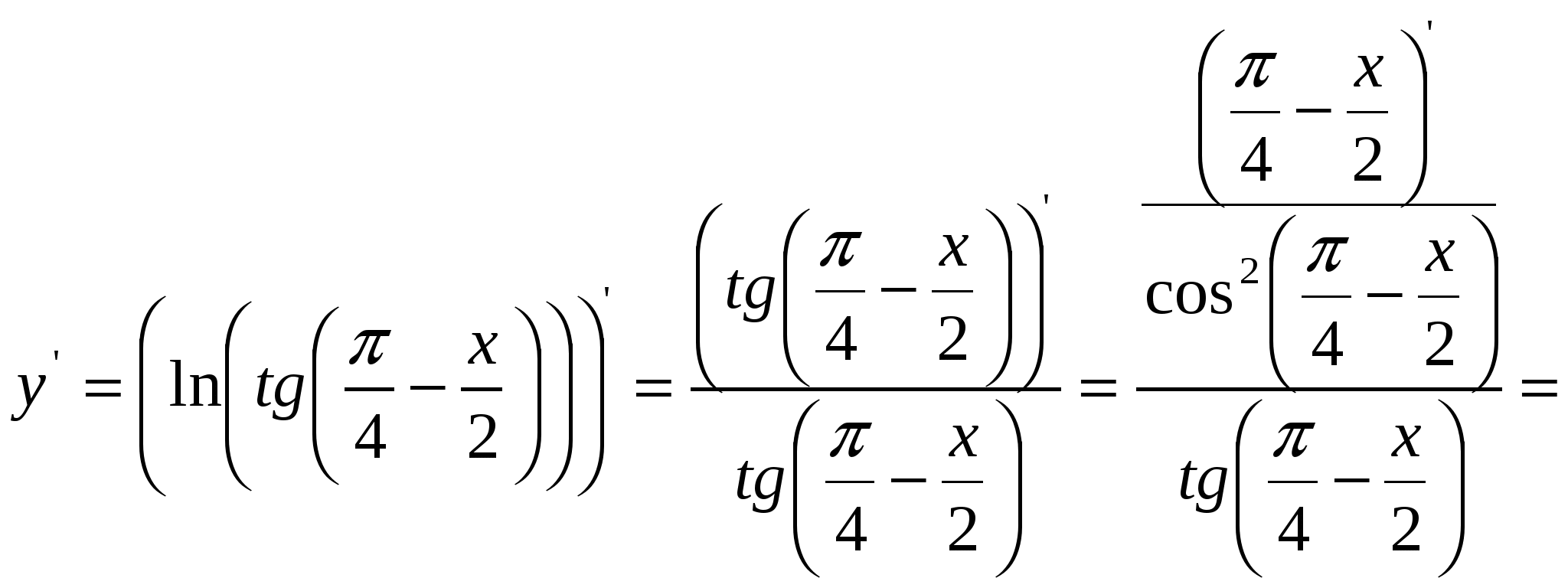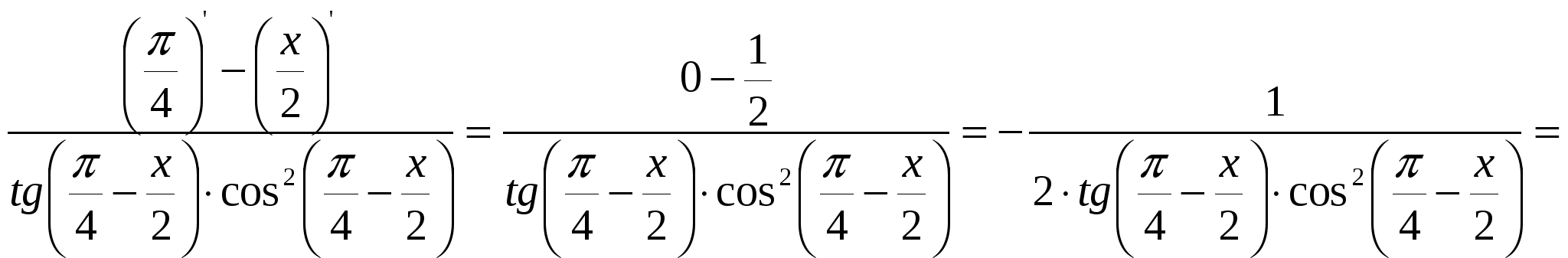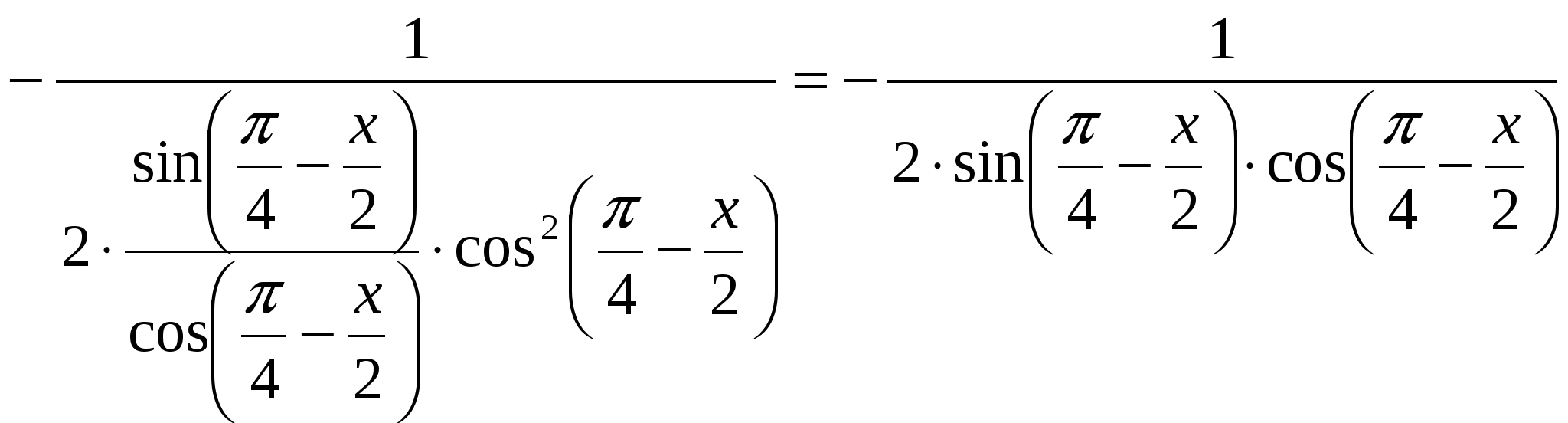


;
г)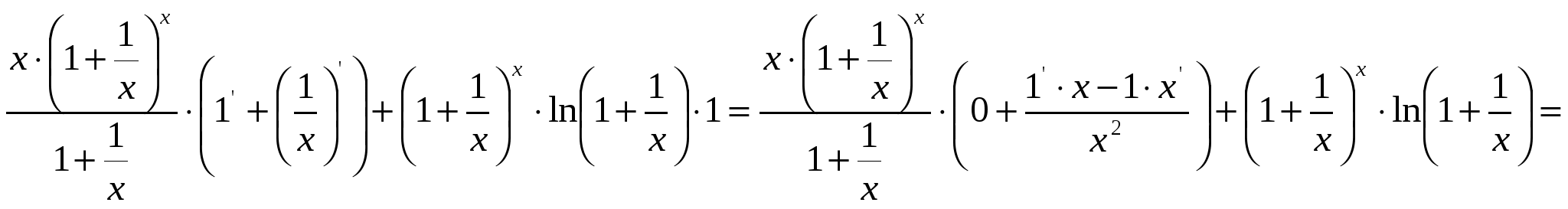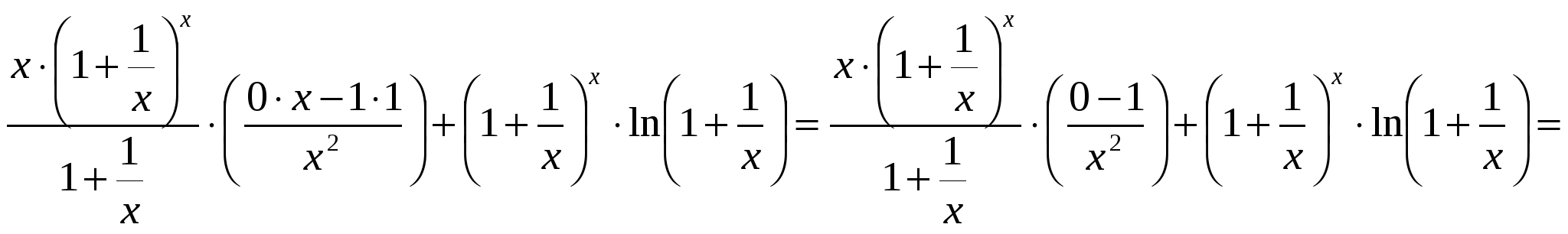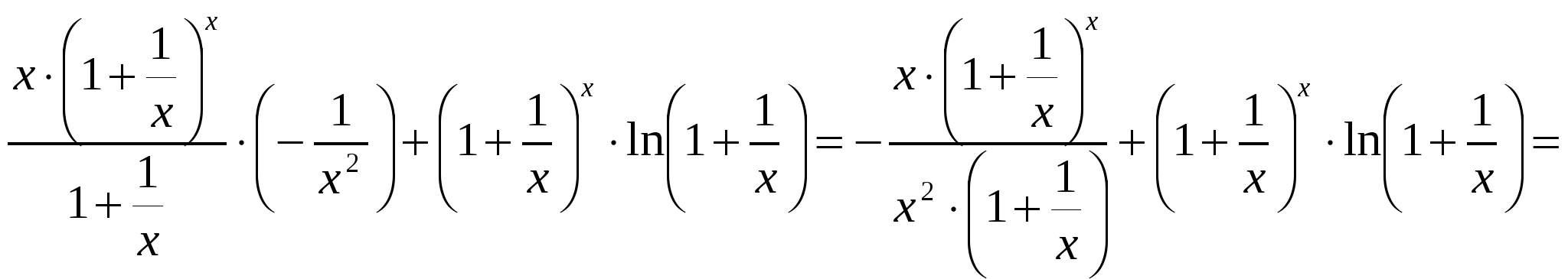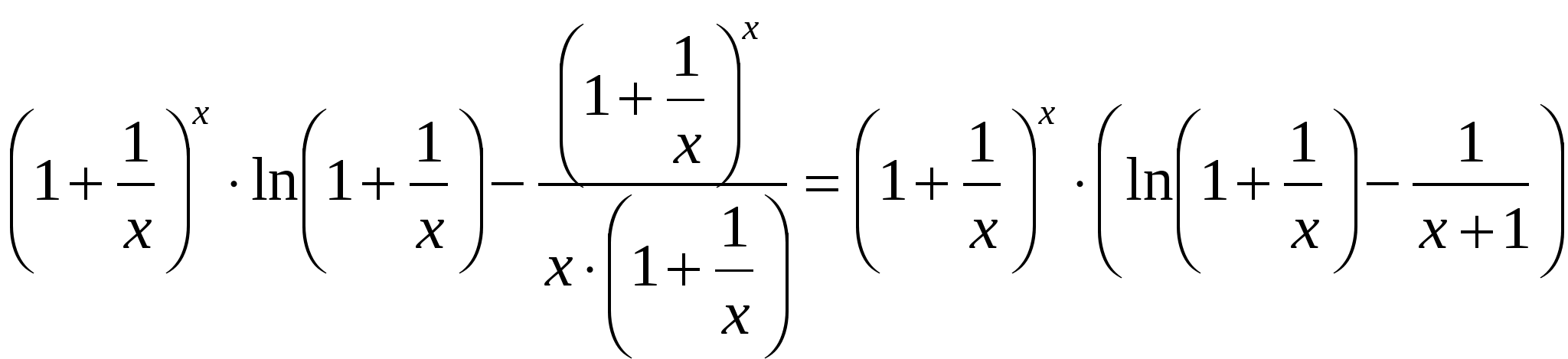





;

д) ; ; ;
; ;
;
; ;
;


57. Найти наибольшее и наименьшее значение функции на указанном отрезке.
.
1) Найдём производную функции: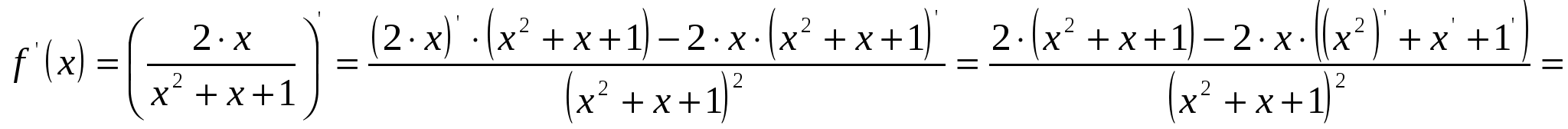




;

2) Найдём критические точки:
; ; ; ; ; ;;
3) Найдём значения функции в критических точках и на концах интервала:
;
;
;
;
Следовательно: ; .
67. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить график.

.

1) Область определения функции: ; ;; ;

2) Чётность, нечётность функции:

; . Следовательно, функция не является ни чётной, ни нечётной – общего вида.

3) Пересечение с осями координат:

- С :; ; ;

- С : ; . Точка является пересечением с осями координат.

4) Экстремумы функции.

Для нахождения точек экстремума найдём производную от функции и приравняем её к нулю.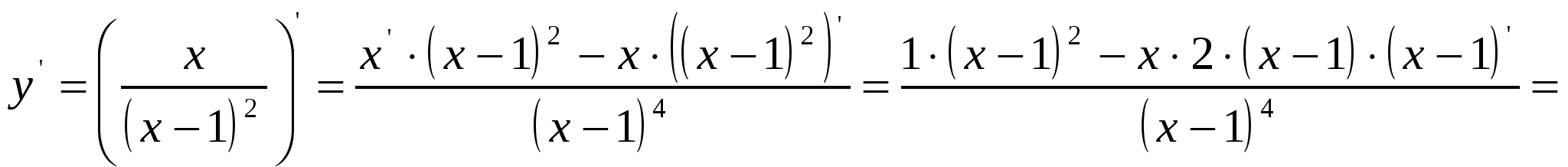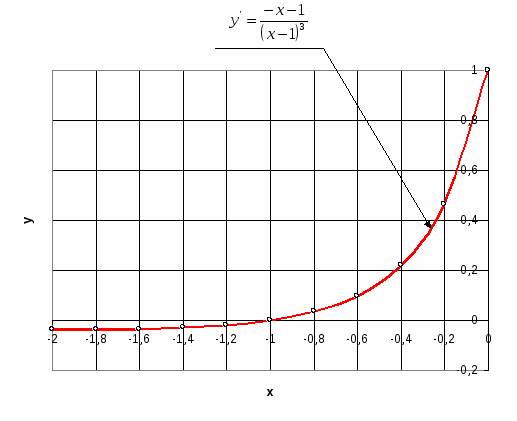





; ; ; ;

.



.

		0

При переходе через точку производная меняет свой знак с «-» на «+». Значит, точка является точкой минимума. Функция возрастает на интервалах: и убывает на промежутке: .
5) Выпуклость, вогнутость функции.
Для нахождения точек перегиба найдём вторую производную от функции и приравняем её к нулю.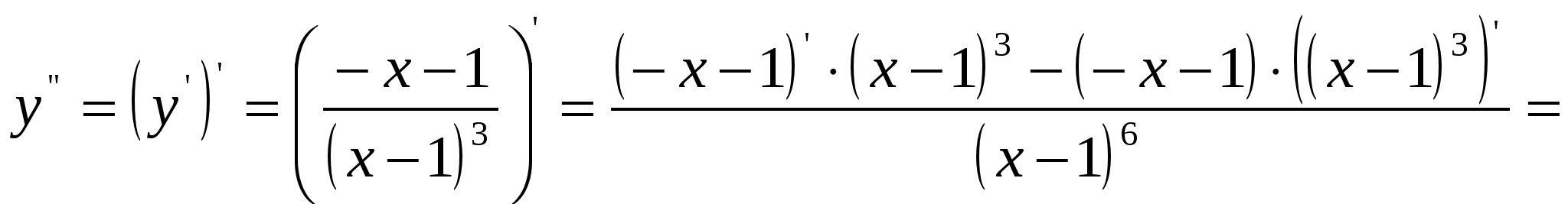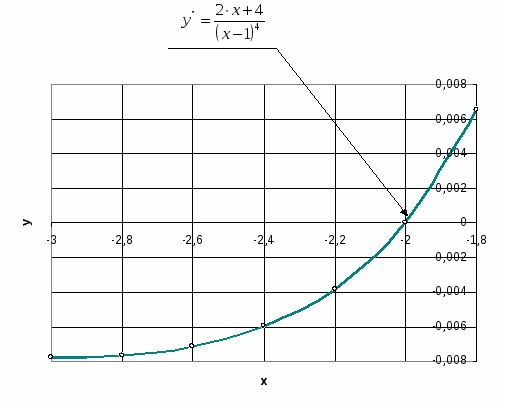








; ; ;; ; .

		0
	выпуклая	точка перегиба	вогнутая

Функция выпуклая на интервале: и вогнутая на интервале: .
6) Асимптоты:

Горизонтальные асимптоты: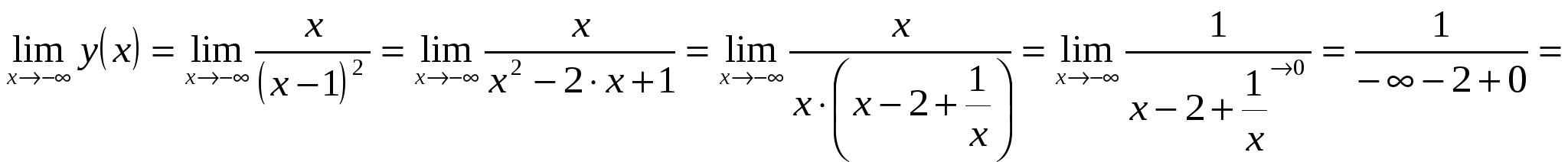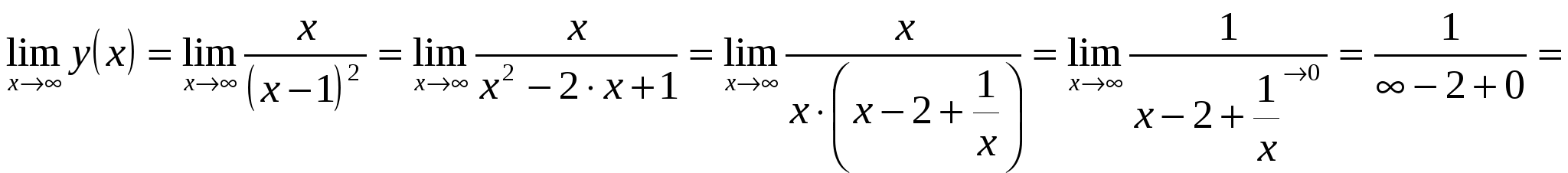

;


;

Следовательно, горизонтальных асимптот нет.
Вертикальные асимптоты:
Найдём вертикальные асимптоты графика функции с помощью односторонних пределов:
;

.

Следовательно: - вертикальная асимптота графика функции.

Наклонные асимптоты:
Уравнение наклонной асимптоты имеет вид: 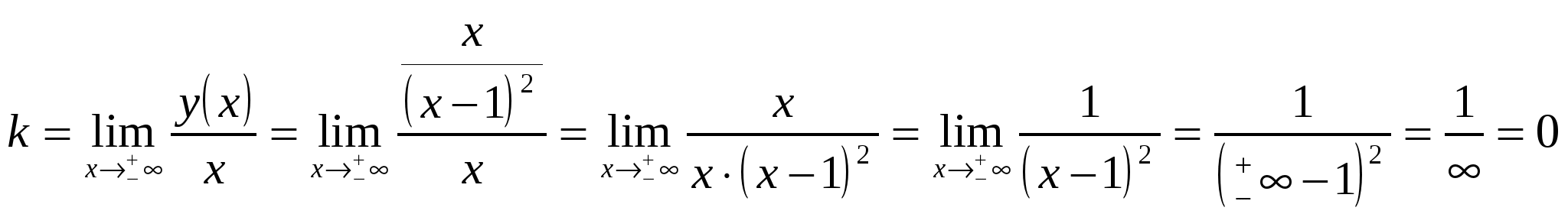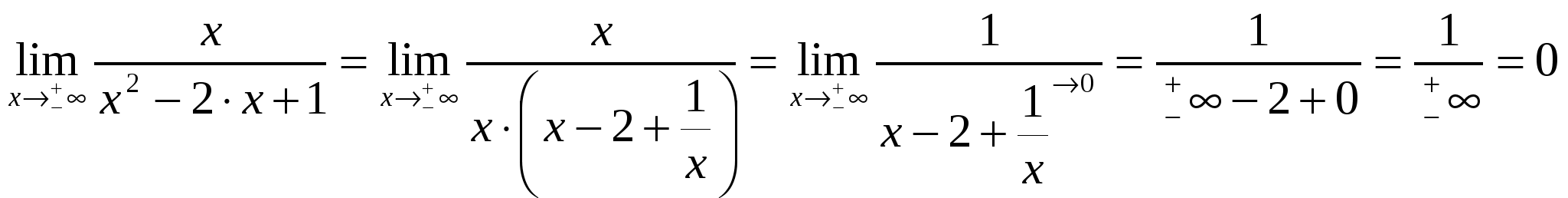, где

;



.
Следовательно: - уравнение наклонной асимптоты.

7) График функции: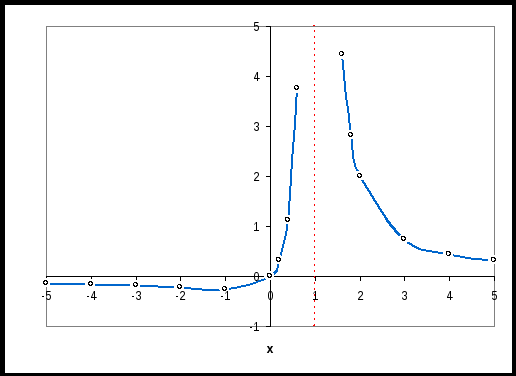



77. Вычислить полный дифференциал , если .

1) Найдём частные производные первого порядка: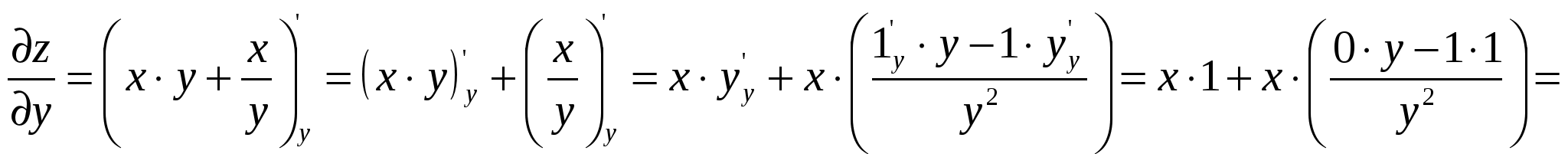
;

;

2) Найдём частные производные второго порядка: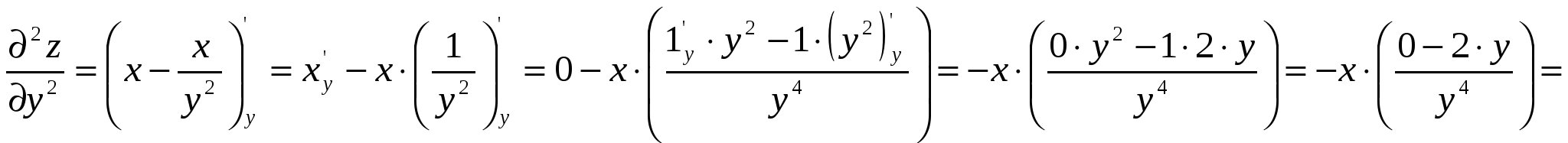
;

;


. Следовательно:
.
87. Даны функция , точка и вектор . Найти:
1) в точке ;

2) Производную в точке 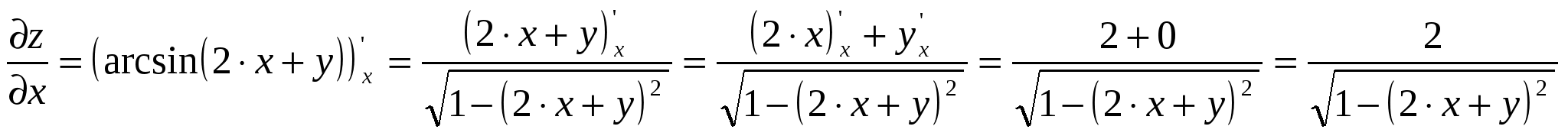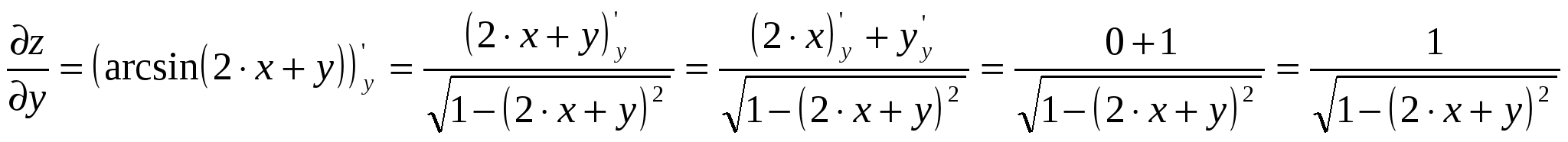по направлению вектора .

1) ;

;

;
;
;
;
2) . Найдём направляющие косинусы:

; ;
. Следовательно, функция в точке по направлению вектора возрастает.

97. Экспериментально получены пять значений искомой функции при пяти значениях аргумента, которые записаны в таблице:

	1	2	3	4	5
	5,3	4,2	4,0	3,2	2,3

Методом наименьших квадратов найти функцию вида , выражающую приближённо (аппроксимирующую) функцию . Сделать чертёж, на котором в прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции .
Решение:
По методу наименьших квадратов коэффициенты 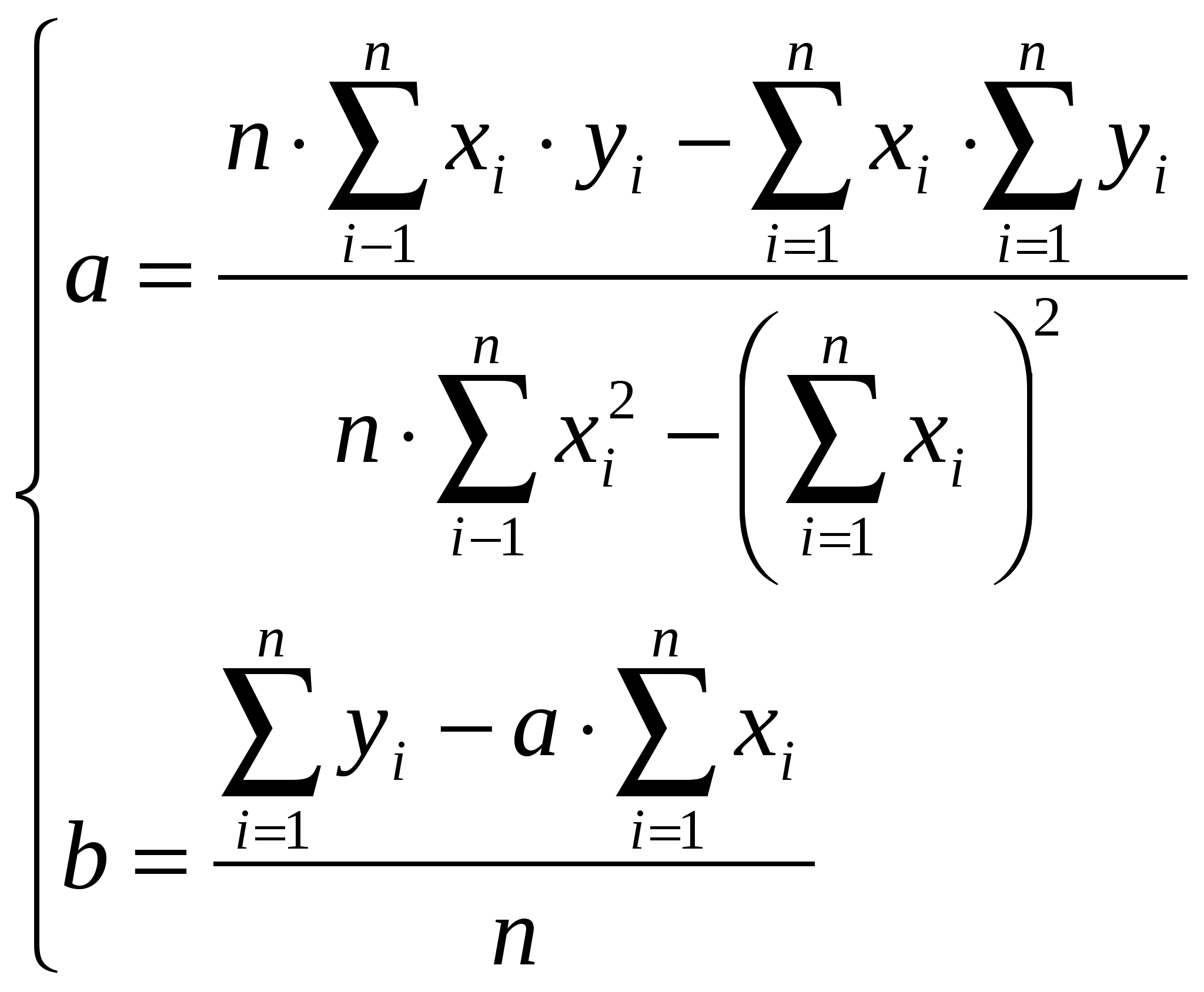и находятся по формулам.



Составим таблицу:

	1	2	3	4	5	15
	5,3	4,2	4,0	3,2	2,3	19
	5,3	8,4	12	12,8	11,5	50
	1	4	9	16	25	55

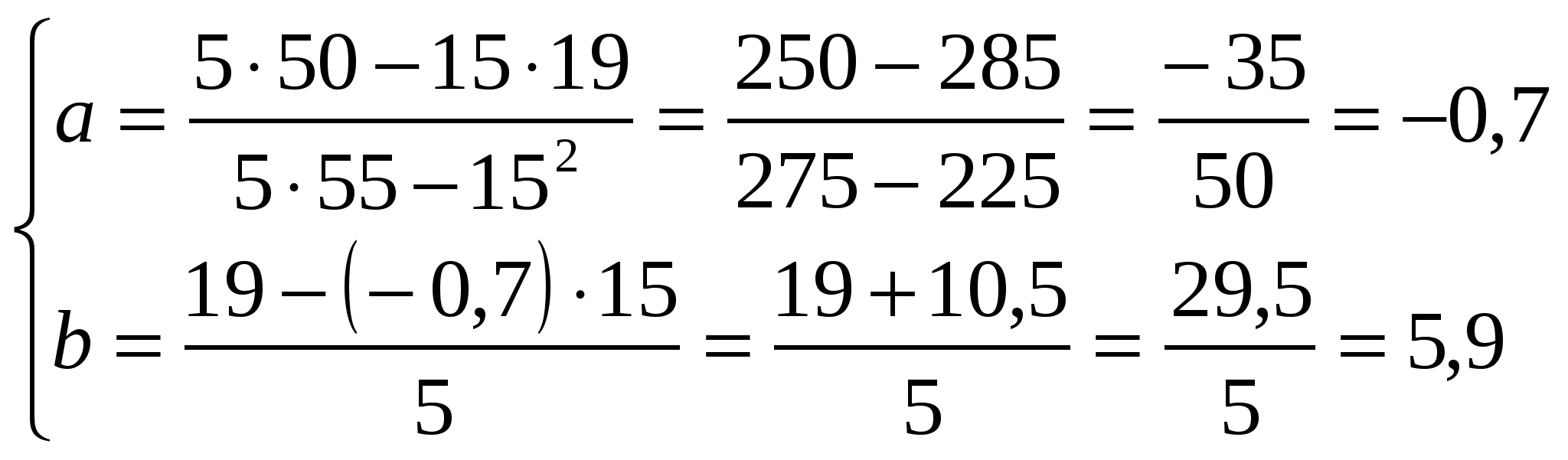Следовательно: 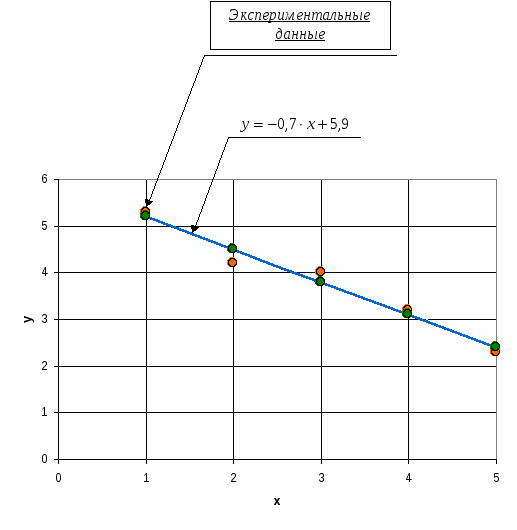.