Контрольная по сопромату. Документ Microsoft Office Word. Литература 14 Здание 1. Тест. Прочность конструкции это
 Скачать 139.79 Kb.
|
|
Содержание Здание №1. Тест. 2 Здание №2. Контрольные вопросы к зачету. 8 Здание №3. 10 Литература 14 Здание №1. Тест.1. Прочность конструкции это: А. способность нагруженной конструкций сопротивляться разрушению; Б. способность конструкции сопротивляться деформациям; В. способность конструкции восстанавливать форму после снятия нагрузки. 2. Гипотеза изотропности описывает материал, свойства которого: А. описаны законом Гука Б. зависят от способа приложения нагрузки; В. не зависят от направления рассмотрения; 3. Материал относят к упругим, если: А. он полностью восстанавливается после снятия внешней нагрузки; Б. не разрушается при произвольной нагрузке; В. имеет остаточные деформации. 4. Метод сечений позволяет определить: А. внутренние усилия внутри тела; Б. моменты инерции сечения; В. прочность тела в заданном сечении. 5. Нормальные напряжения это: А. сила, действующая на единицу площади, направленная перпендикулярно проведенному сечению; Б. усилие вдоль приложенной внешней силы; В. сумма всех напряжений в точке. 6. Касательные напряжения это: А. напряжения в плоскости сечения; Б. деформации в плоскости сечения; В. усилия в касательной плоскости. 7. Нормальное напряжение при растяжении стержня равно: А. М/W; Б. p*cosα; В. P/F 8. Наибольшие нормальные напряжения при одноосном растяжении достигаются под углом: А. α=0; Б. α=350; В. α=450. 9. Главные напряжения определяются как: А. нормальные напряжения на площадках, где касательные напряжения равны 0; Б. наибольшие касательные напряжения; В. сумма нормальных напряжений. 10. Для решения статически неопределимых задач кроме уравнений равновесия необходимо: А. уравнение совместности деформаций; Б. условие прочности; В. условие жесткости. 11. При положительном изгибающем моменте верхние волокна балки испытывают: А. сжатие; Б. растяжение; В. кручение. 12. Чтобы найти экстремум на эпюре моментов, надо: А. приравнять Q нулю; Б. составить уравнение равновесия; В. экстремум всегда на опоре балки. 13. Скачок на эпюре моментов в балках наблюдается в местах: А. где приложен внешний момент; Б. где действует минимальная распределенная нагрузка; В. в обоих случаях. 14. Нормальные напряжения в балках максимальны на участках действия: А. максимальной перерезывающей силы; Б. максимального изгибающего момента; В. максимального крутящего момента. 15. Максимальные напряжения при изгибе равны: А. M/W Б. Q/W В. Q/F 16. Момент сопротивления прямоугольного сечения шириной b и высотой h равен: А. bh/6 Б. bh2/6 В. bh3/6 17. Момент инерции прямоугольного сечения шириной b и высотой h равен: А. bh/12 Б. bh3/12 В. bh3/6 18. Какие внутренние силовые факторы возникают в брусе при чистом сдвиге: А. поперечная сила; Б. изгибающий момент; В. поперечная сила и изгибающий момент. 19. Что означает выражение σ≤[σ] А. закон Гука; Б. условие прочности; В. коэффициент запаса. 20. Способность материала сопротивляться деформациям называется: А. прочность; Б. жесткость; В. устойчивость. 21. Что такое момент силы? Момент силы - векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. 22. Охарактеризуйте основные типы опор. Существуют виды опор (рисунок 1). 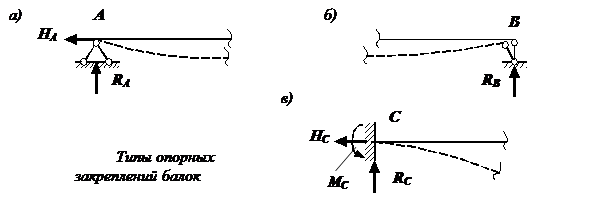 Рисунок 1 – Виды опор: а) шарнирно неподвижная опора; б) шарнирно подвижная опора; в) жесткая заделка. Шарнирно неподвижная опора (рис. а, опора А) - это закрепление конца балки, при котором балка может поворачиваться, но не может перемещаться ни в горизонтальном (влево или вправо), ни в вертикальном (вверх или вниз) направлениях, то есть не может перемещаться ни в каком направлении. В шарнирно неподвижной опоре может возникнуть реакция, которую удобно представить в виде двух составляющих: вертикальной (  ) и горизонтальной ( ).Шарнирно неподвижная опора на расчетной схеме условно изображается посредством двух стерженьков. Нижние их концы шарнирно прикреплены к «земле», а верхние концы соединены между собой и с балкой шарниром. Шарнирно подвижная опора Шарнирно подвижная опора (рис. б, опора B) - это устройство, в котором конец балки может свободно перемещаться в горизонтальном направлении, может поворачиваться при изгибе, но не может перемещаться в вертикальном направлении. Со стороны шарнирно подвижной опоры может возникнуть только вертикальная реакция (  ). Шарнирно подвижная опора изображается посредством одного стерженька, шарнирно соединенного и с землей, и с балкой.Жесткая заделка Жесткая заделка - это закрепление (рис. в), при котором конец балки не может ни поворачиваться, ни перемещаться. В заделке могут возникнуть реактивный момент  (момент жесткой заделки) и реакции  и  . Балка при жестком закреплении показывается заделанной в часть стены, которая штрихуется.23. Что называется вектором полного перемещения точки? Вектором полного перемещения точки деформируемого тела называется вектор, соединяющий две точки деформированного тела. имеющий начало в точке недеформированного тела, а конец в той же точке деформированного тела. 24. Что называется коэффициентом поперечной деформации (коэффициентом Пуассона) и в каких пределах он изменяется? Коэффициентом Пуассона называется отношение относительных деформаций поперечной e x к продольной e z, взятое с обратным знаком, в случае, если действуют только вертикальные напряжения s z (напряжения s x и s y в этом случае отсутствуют). Коэффициент Пуассона изменяется теоретически от 1 до +0,5, а практически от 0 до +0,5. Коэффициент Пуассона не может быть более 0,5, так как в этом случае при всестороннем сжатии (s x=s y=s z) должен был бы увеличиваться объем грунта, что физически невозможно. 25. Что такое устойчивость в сопротивлении материалов? Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях. Обычно потеря устойчивости системы сопровождается большими перемещениями, возникновением пластических деформаций или разрушением. Возможны также случаи, когда система, потеряв устойчивость, переходит в режим незатухающих колебаний. Здание №2. Контрольные вопросы к зачету.Блок №1 Вар.11 (21). Что называется жесткостью поперечного сечения при растяжении? Жесткость поперечного сечения - это способность сечения (стержня с заданным сечением) сопротивляться деформированию. Для четырех основных видов деформаций жесткость сечения определяется так: EAEA - растяжение - сжатие GAGA - сдвиг EJxEJx - изгиб GJρGJρ - кручение Блок №2 Вар.11 (21). Что называется хрупкостью? Хрупкость - способность материала разрушаться без заметных пластических деформаций. Xрупкость противоположна пластичности; факторы, повышающие пластичность, уменьшают хрупкость и наоборот. Хрупкие материалы разрушаются без заметной пластической деформации уже при статических испытаниях (напр., стекло, чугуны и др.). Если материал пластичен при статических испытаниях и хрупко разрушается при динамиески, говорят об ударной хрупкости. Такие материалы, как свинец, медь и др., пластичны при всех испытаниях. Иногда считают, что причиной ударной хрупкости является различное влияние скорости деформации на изменение сопротивления деформации и изменение сопротивления разрушению, причем первое из них есть предел текучести, а второе — предел прочности при данной температуре, скорости и степени деформации, а также схеме напряженного состояния. Если сопротивление деформации окажется равным или больше сопротивления отрыву, это приведет к хрупкому разрушению материала. Если сопротивление деформации при некоторой скорости деформации растет быстрее сопротивления разрушению, пластичность материала уменьшается. Хрупкое состояние зависит от многих факторов. Большое влияние на хрупкость оказывает напряженное состояние: чем неоднороднее напряженное состояние, тем легче переход от пластичности к хрупкости. Однородное напряженное состояние способствует увеличению пластичности. Размеры и форма тела также влияют на хрупкость: чем больше размеры тела, тем вероятнее в нем наличие пустот, пузырей и других дефектов, которые также являются концентраторами напряжений. Существ, влияние на хрупкость оказывают микро- и макроструктура. Например, у металлов чем сложнее сплав и неоднороднее структура, тем меньше пластичность. Литая структура обнаруживает большую хрупкость в сопротивлении материалов, чем деформированная. Хрупкость бетона зависит от размеров формы камневидной составляющей и водоцементного отношения. Поведение некоторых материалов зависит от направления деформирования (дерево, отливки из цинка). Изменение температуры может существенно влиять на хрупкость в сопротивлении материалов, т. к. с ее изменением связаны структурные преобразования (у металлов, пластмасс), изменение влажности, появление внутренних напряжений и, вследствие этого, неоднородности напряженного состояния. Понижение температуры приводит к увеличению хрупкости., т. к. при этом предел текучести увеличивается быстрее, чем предел прочности. С повышением температуры хрупкость в сопротивлении материалов уменьшается, но при этом всегда необходимо учитывать возможные структурные преобразования, изменение влажности, напряженного состояния и др. Здание №3.Решить задачу (вариант 11). Дан изгибаемый стержень, имеющий длину l (принимается по вариантам в таблице 1). К середине стержня приложена вертикальная сосредоточенная нагрузка F = 10кН. 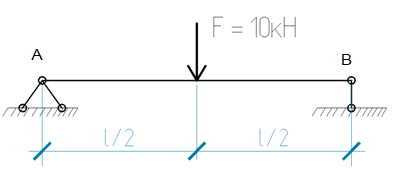 Таблица 1 Исходные данные
Требуется: - определить значение максимального изгибающего момента; - определить значение перерезывающих сил; - построить эпюру изгибающих моментов; - построить эпюру поперечных сил. Решение Перерезывающая сила Q, действующая в каком-либо сечении балки, является равнодействующей внутренних касательных усилий и численно равна сумме внешних сил, действующих по одну сторону от рассматриваемого сечения. Изгибающий момент М, образованный системой сжимающих и растягивающих внутренних нормальных усилий, численно равен алгебраической сумме моментов внешних сил, действующих по одну сторону от рассматриваемого сечения 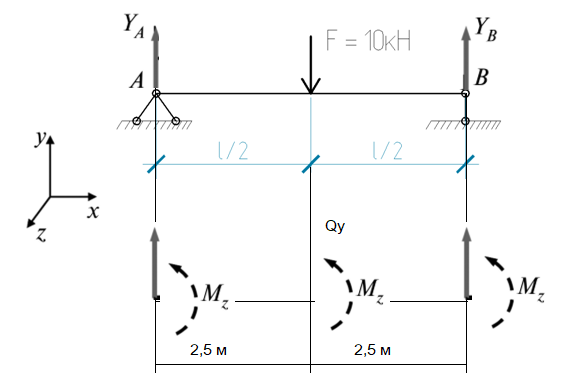  Составим уравнения равновесия для определения реакций опор Σ MA = F · 2,5 - RC · 5= 10 · 2,5 - RC · 5=0 Σ MC = - F · 2,5 + RA · 5= - 10 · 2,5 + RA · 5=0 Σ MA =2,5·F-5·RC=25-5·RC=0 Σ MC =-2,5·F+5·RA=-25·RA+5·RA=0 Из этих уравнений находим реакции опор RA = 5 кН. RC = 5 кН. Проверка ΣY = + RA + RC - F = + 5 + 5 - 10 = 0 Записываем уравнения поперечных сил и изгибающих моментов на участках стержня, используя метод сечений На участке AB: (0 ≤ z1 ≤ 2,5 м ) Q(z1) = + RA = + 5 = 5 кН M(z1) = + RA · z = + 5 · z M(0) = 0 кНм M(2,5) = 15 кНм На участке BC: (3 ≤ z2 ≤ 6 м ) Q(z2) = + RA - F = + 5 - 10 = -5 кН M(z2) = + RA · z - F·(z - 3) = + 5 · z - 10·(z - 3) M(2,5) = 15 кНм M(5) = 0 кНм Максимальный момент в балке составляет Mmax = 15 кНм. Перерезающая сила 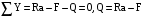 Q=5-10=-5 кН Проверка: Q=5-10+5=0 Эпюра изгибающих моментов и поперечных сил показана на рисунке 2. 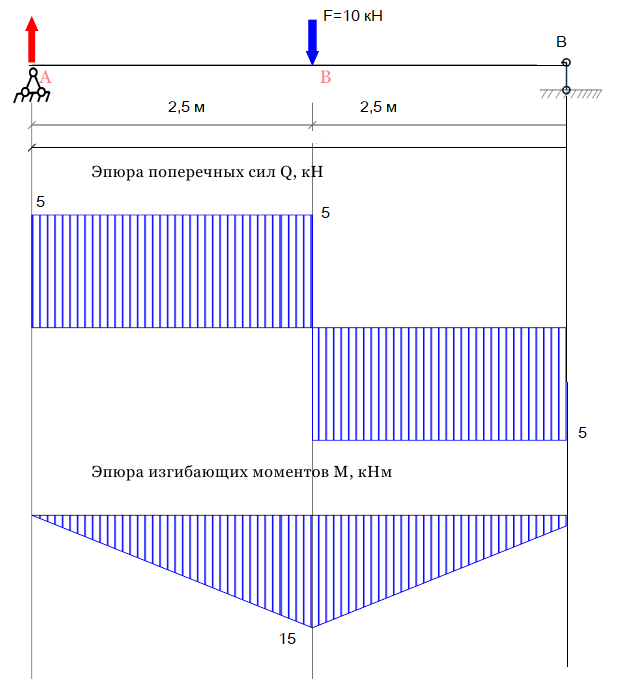 Рисунок 2 – Эпюра изгибающих моментов и поперечных сил Литература1. Кузьмин, Л.Ю. Строительная механика. [Электронный ресурс] :Учебные пособия / Л.Ю. Кузьмин, В.Н. Сергиенко. — Электрон, дан. — СПб.:Лань, 2016. — 296 с. - ЭБС Лань. 2. Васильков, Г.В. Строительная механика. Динамика и устойчивость сооружений. [Электронный ресурс] :Учебные пособия / Г.В. Васильков, З.В. Буйко. — Электрон, дан. — СПб. : Лань, 2013. — 256 с. - ЭБС Лань. 3. Сопротивление материалов: Учеб. Для вузов/А.В. Александров А. В., В.Д. Потапов, Б.П. Державин; Под ред. А.В. Александрова. – 3-е изд. Испр. – М.: Высш. Шк. 2003 – 560 с. 4. Вансович, К. А. Строительные конструкции: учеб. пособие : в 2 ч. / К. А. Вансович. -Омск : Изд-во ОмГТУ. - 2012. - Ч. 2. - 91 с. 5. Дарков А.В., Шапиро Г.С. Сопротивление материалов. 5-е изд., перераб. — М.: Высшая школа, 1989. — 624 с. 6. Костенко Н.А. и др. Сопротивление материалов. – М.: Высшая школа, 2004. – 430c. |