курсач дифференциальные уравнения в физике. Литература 16 Введение. Дифференциальные уравнения
 Скачать 58.03 Kb. Скачать 58.03 Kb.
|
|
План План 2 Введение 3 Задачи 4 Заключение 15 Литература 16 Введение. «Дифференциальные уравнения» как дисциплина содержит в себе не только обучение решению уравнений, но и включает в себя большой спектр практического применения дифференциальных уравнений. Разные науки (биология, химия, физика) имеют задачи, основными методами решения которых является составление и решение дифференциальных уравнений. Довольно часто при изучении многих процессов, протекающих в природе, бывает сложно установить зависимость между функциями, характеризующими те или иные величины. Но зато, в некоторых случаях, возможно установить связь между теми же функциями и их производными. Это приводит к уравнениям, содержащим неизвестные функции под знаком производной, то есть к дифференциальным уравнениям (с их помощью процесс может быть описан проще и полнее). Изучая те или иные процессы, ученые могут составить соответствующие им дифференциальные уравнения. А затем, решая это уравнение, удается вывести функциональный закон описания изучаемого вопроса. Практически любой биологический процесс подчиняется тому или иному дифференциальному уравнению. Например: процесс размножения бактерий, явление органического роста, изменение давления при подъеме над уровнем моря. Можно также написать дифференциальные уравнения движения планеты вокруг Солнца, искусственного спутника вокруг Земли. Цель этой курсовой работы – рассмотреть некоторые физические задачи и процессы, при решении которых необходимы дифференциальные уравнения. Задача 1. Линейное движение частицы в жидкостях и газах. Составить уравнение скорости для тела, погружающегося в жидкость. Решение. [3] Когда анализируется механическая система, чтобы определить уравнение движения, часто ссылаются на предположение, что в системе нет трения или диссипативных сил. Обычно, это описание реалистично только в определенной степени, а иногда и совершенно нереалистично, но дифференциальное уравнение, описывающее динамику системы, может быть решено только в некоторых случаях, когда диссипативные силы (возникающие от трения или вязкости) не зависят от скорости. Последнее относится к тому случаю, когда твердые материалы перемещаются относительно друг друга. Сначала мы рассмотрим тело (шар), которое погружается в жидкость (воду) под действием силы тяжести. Если скорость не слишком велика (а для малых тел это так), мы имеем так называемое ламинарное течение, и в этом случае мы можем предположить, что сопротивление движению пропорционально скорости тонущего тела. Если скорость движения становится больше, сопротивление превращается в турбулентный поток, где сопротивление движению более заметно, но эмпирически предполагается, что оно пропорционально квадрату скорости. Турбулентность лучше всего описывается появлением вихрей в жидкости или в воздухе. Кстати, турбулентность все еще является одной из частично нерешенных проблем гидродинамики, поскольку уравнения Навье-Стокса (второй закон Ньютона для гидродинамики) не допускают перехода от ламинарного потока к турбулентному потоку, хотя оба явления появляются как решение уравнений. Теоретическое выражение для вязкой силы, действующей на шар в ламинарном потоке, впервые дано Стоксом и называется законом Стокса. Если r - радиус шара, v - скорость, = вязкость жидкости, то: 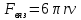 В следующих примерах мы сократим константы  до единицы, а затем запишем пропорциональность между силой и скоростью следующим образом: до единицы, а затем запишем пропорциональность между силой и скоростью следующим образом: 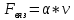 . .Эта формула фактически не зависит от формы падающего тела, если поток ламинарный. Для движения вдоль оси x у нас есть хорошо известные формулы. Скорость: 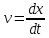 , ,ускорение: 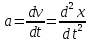 и второй закон Ньютона: 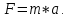 На тело, погруженное в жидкость, действуют следующие силы: Выталкивающая сила: 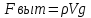 где 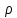 - плотность жидкости, а - плотность жидкости, а 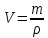 - объем тела с массой m и плотностью - объем тела с массой m и плотностью 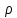 . .Сила тяжести: 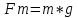 Сила вязкости: 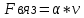 Следовательно, результирующая сила, действующая на тело, равна: 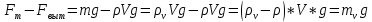 Где 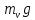 - сила тяжести тела, без силы выталкивания. - сила тяжести тела, без силы выталкивания.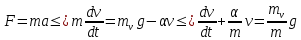 Для большей простоты запишем: 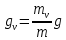 Уравнение решается методом умножения на 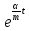 и перестановки. и перестановки.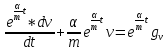 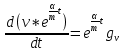 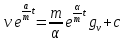 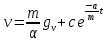 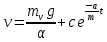 Добавляя начальное условие 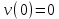 , мы находим , мы находим 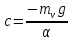 , что в решении дает: , что в решении дает: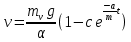 Мы видим, что скорость асимптотически приближается к: 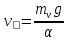 . .Период «полураспада» скорости можно определить традиционным способом: 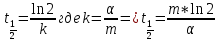 Для большинства движений в жидкостях конечная скорость достигается довольно быстро. Уравнение можно интегрировать, чтобы получить расстояние x. 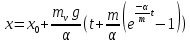 Если тело имеет начальную скорость 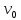 , противоположную силе тяжести, мы должны изменить знак члена mg и , противоположную силе тяжести, мы должны изменить знак члена mg и 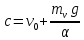 . . В этом случае мы находим решение: 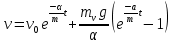 . .Скорость снова асимптотически приближается к: 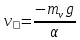 . .Ответ: 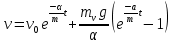 Задача 2. Материальная точка массы m замедляет своё движение под действием силы сопротивления среды, пропорциональной квадрату скорости v. [1] Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если 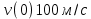 , а , а 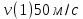 . . Решение. Примем за независимую переменную время t , отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки v будет функцией t , т.е. 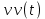 . Для нахождения . Для нахождения 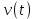 воспользуемся вторым законом Ньютона: F ma , где a v(t) есть ускорение движущегося тела, F – результирующая сила, действующая на тело в процессе движения. воспользуемся вторым законом Ньютона: F ma , где a v(t) есть ускорение движущегося тела, F – результирующая сила, действующая на тело в процессе движения. В данном случае, 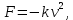 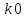 – коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция v v(t) является решением дифференциального уравнения: – коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция v v(t) является решением дифференциального уравнения: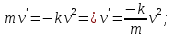 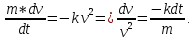 Интегрируем: 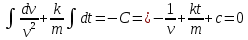 Отсюда 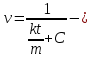 общее решение дифференциального уравнения в явном виде. общее решение дифференциального уравнения в явном виде.Найдем параметры 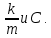 Согласно условию задачи, имеем: Согласно условию задачи, имеем: и и 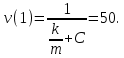 Отсюда 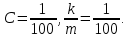 Следовательно, скорость точки изменяется по закону 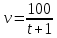 . .Поэтому 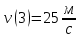 . .Ответ: 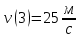 . .Задача 3. Вещество переходит в раствор. Написать уравнение перехода вещества в раствор. Решение. [1] Пусть количество вещества, переходящего в раствор, пропорционально интервалу времени и разности между максимально возможной концентрацией P и концентрацией x в данный момент времени: 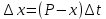 . .В форме дифференциального уравнения этот закон выглядит так: 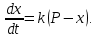 Разделим в этом уравнении переменные и проинтегрируем: 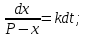 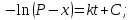  . .Если  . .График этой функции представлен на рисунке:  Задача 4. Уравнение движения груза. [2]Найти уравнение движения груза массой 200 г, закрепленного на легкой вертикальной пружине с коэффициентом жесткости 5 кг/с2, если первоначально груз был отклонен от положения равновесия на 2 см и затем отпущен без начальной скорости. Известно, что при движении данного груза со скоростью 10 м/с сопротивление воздуха составляет 1 Н. Решение. Пусть  — это отклонение груза от положения равновесия в момент времени — это отклонение груза от положения равновесия в момент времени  . На груз действуют сила упругости пружины . На груз действуют сила упругости пружины  и сила сопротивления воздуха, которую будем считать пропорциональной скорости груза, т.е. и сила сопротивления воздуха, которую будем считать пропорциональной скорости груза, т.е.  , где , где  . .Получим дифференциальное уравнение: 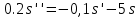 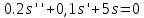 . .Характеристическое уравнение имеет корни: 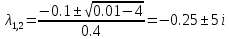 , ,поэтому общее решение выглядит следующим образом: 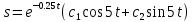 Дифференцируя, найдем скорость: 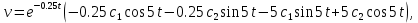 и из начальных условий 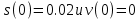 вычислим константы: 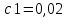 и и  . .Следовательно, окончательно уравнение движения груза приобретает вид: 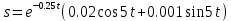 Ответ: 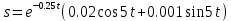 . .Задача 5. Реактивное движение. [2] Ракета с нулевой начальной скоростью движется прямолинейно под действием отдачи от струи газа, исходящей со скоростью 2 км/с. Масса ракеты с полным запасом топлива равна 400 т, без топлива — 50 т. Найти скорость движения ракеты после сгорания всего топлива, пренебрегая силой тяжести и сопротивлением воздуха. Решение. Пусть m(t) и v(t) — это масса и скорость ракеты соответственно в момент времени t. Тогда уравнение Мещерского запишется в виде: 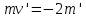 или или 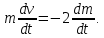 Домножив обе части равенства на dt и введя в рассмотрение функцию v(m), получим дифференциальное уравнение с разделяющимися переменными 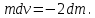 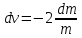 , ,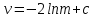 - общее решение. - общее решение.Из условия v(400) = 0 находим, что 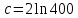 и и 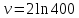 — частное решение. — частное решение.Подставив m = 50 , получим, что после сгорания топлива скорость корабля достигнет значения  . .Ответ: 4,16 км/с. В ходе решения данной задачи мы фактически вывели формулу скорости космического аппарата  , которая впервые была получена Циолковским в 1897 году и сейчас носит его имя. В этой формуле через M и m обозначены начальная и конечная (после выработки топлива) массы космического аппарата, через u — скорость газовой струи. Скорость ракеты v, вычисляемую по формуле Циолковского, называют характеристической. Реальная же скорость, как правило, ниже характеристической из-за влияния сил гравитации и сопротивления среды, а также из-за потерь, вызванных затратами на управление движением космического корабля. , которая впервые была получена Циолковским в 1897 году и сейчас носит его имя. В этой формуле через M и m обозначены начальная и конечная (после выработки топлива) массы космического аппарата, через u — скорость газовой струи. Скорость ракеты v, вычисляемую по формуле Циолковского, называют характеристической. Реальная же скорость, как правило, ниже характеристической из-за влияния сил гравитации и сопротивления среды, а также из-за потерь, вызванных затратами на управление движением космического корабля. Задача 6. Нагревание и охлаждение. [2] Тело охладилось за 10 мин от 70 до 40 °C. Температура окружающей среды поддерживается равной 25 °C. Сколько еще минут понадобится, чтобы тело остыло до 30 °C? Решение. Пусть  — это температура тела в момент времени t, где температура измеряется в градусах Цельсия, а время — в минутах. Тогда по закону Ньютона — это температура тела в момент времени t, где температура измеряется в градусах Цельсия, а время — в минутах. Тогда по закону Ньютона - уравнение с разделяющимися переменными. - уравнение с разделяющимися переменными.Решаем его: 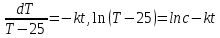 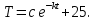 Из условий 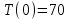 и и 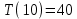 находим, что находим, что 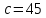 и и 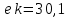 , и закон охлаждения приобретает вид , и закон охлаждения приобретает вид 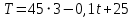 . . Подставив в этот закон 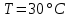 , получим , получим 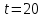 мин. Так как требуется найти время, прошедшее с момента охлаждения тела до 40 °C, то окончательный ответ 20−10 =10 мин. мин. Так как требуется найти время, прошедшее с момента охлаждения тела до 40 °C, то окончательный ответ 20−10 =10 мин.Ответ: 10 мин. В задачах на охлаждение или нагревание тела при взаимодействии с окружающей средой температуру окружающего пространства 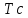 принято считать постоянной. Согласно закону, установленному Ньютоном, скорость охлаждения или нагревания тела пропорциональна разности температур тела и окружающей среды, т.е. принято считать постоянной. Согласно закону, установленному Ньютоном, скорость охлаждения или нагревания тела пропорциональна разности температур тела и окружающей среды, т.е. 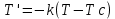 , при этом если в начальный момент времени температура тела T больше температуры окружающего пространства Tc, то происходит охлаждение и скорость T′ отрицательна, а если , при этом если в начальный момент времени температура тела T больше температуры окружающего пространства Tc, то происходит охлаждение и скорость T′ отрицательна, а если 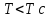 , — нагревание и , — нагревание и 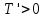 . Сделанное замечание объясняет, почему коэффициент пропорциональности k обычно записывают со знаком минус. Само значение величины k зависит как от физических свойств тела, так и от его геометрической формы. Для нахождения коэффициента, как правило, измеряют температуру тела в некоторый промежуточный момент времени. . Сделанное замечание объясняет, почему коэффициент пропорциональности k обычно записывают со знаком минус. Само значение величины k зависит как от физических свойств тела, так и от его геометрической формы. Для нахождения коэффициента, как правило, измеряют температуру тела в некоторый промежуточный момент времени. Заключение. В данной курсовой работе приведены примеры физических задач, приводящиеся к дифференциальным уравнениям. Были составлены дифференциальные уравнения, удовлетворяющие условиям задач. Опыт развития различных наук показывает, что многие далёкие друг от друга по содержанию задачи приводят к сходным дифференциальным уравнениям. Теория дифференциальных уравнений представляет собой очень богатый содержанием стремительно развивающийся раздел математики. Возможность описать многие процессы, интересующие человека, обеспечивает теории дифференциальных уравнений почетное место в современной науке. Литература Кузьмиченко М. В. Спецкурс для студентов физико-математических факультетов «Приложения дифференциальных уравнений в физике и науках естественно-математического цикла» Научно-методический электронный журнал «Концепт». – 2014. – № 9 (сентябрь). – С. 156–160. Гриншпон Я.С. Геометрические, физические и экономические задачи, сводящиеся к дифференциальным уравнениям: учеб. пособие, 2011 – 74 с. Ole Witt-Hansen, Examples of the Differential equations of Physics, 2008 http://www.olewitthansen.dk/. |
