Литература Ерохин Чернышов, Козырев Антенно фидерные устройства и распространения радиоволн
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
Круглый волновод.Основные понятия.Круглые волноводы наряду с прямоугольными получили достаточно широкое применение. Например, отрезки круглого волновода применяются как элементы вращающихся сочленений предназначенных для передачи электромагнитной энергии от неподвижных волноводов к подвижным, кроме того отрезки круглого волновода могут использоваться как облучатели антенн. Закороченный с двух сторон отрезок круглого волновода применяется как электро магнитный резонатор. Так как фактически круглый волновод является цилиндрической направляющей системой то для описания составляющих электромагнитного поля в нем применяется цилиндрическая система координат (Рис.23). 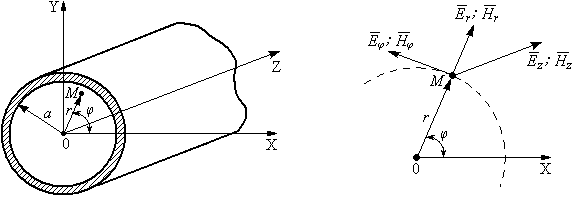 Рис. 23. Круглый волновод в цилиндрической системе координат: 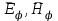 - тангенциальные составляющие векторов электрического и магнитного полей; - тангенциальные составляющие векторов электрического и магнитного полей; 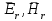 - нормальные составляющие векторов электрического и магнитного полей; - нормальные составляющие векторов электрического и магнитного полей; 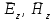 - продольные составляющие векторов электрического и магнитного полей - продольные составляющие векторов электрического и магнитного полейВ круглых волноводах так же как и в прямоугольных могут существовать волны 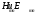 . Продольные составляющие векторов напряженности электромагнитного поля ( . Продольные составляющие векторов напряженности электромагнитного поля (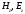 ) так же будут являтся решением мембранного уравнения но в цилиндрической системе координат. ) так же будут являтся решением мембранного уравнения но в цилиндрической системе координат.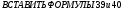 Поскольку распределение по 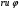 независят друг от друга то выражения для продольных составляющих векторов напряженности магнитного и электрического полей можно выразить через функции Бесселя. независят друг от друга то выражения для продольных составляющих векторов напряженности магнитного и электрического полей можно выразить через функции Бесселя.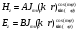 где, где,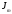 - функция Бесселя первого рода m-го порядка - функция Бесселя первого рода m-го порядка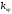 -критическое волновое число -критическое волновое число 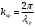 По известным 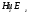 используя приведенное ранее соотношение электродинами (20) можно рассчитывать остальные составляющие поля. При некоторых значениях r составляющие используя приведенное ранее соотношение электродинами (20) можно рассчитывать остальные составляющие поля. При некоторых значениях r составляющие 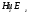 могут обращаться в 0. Из этого условия при могут обращаться в 0. Из этого условия при 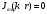 рассчитываются корни функции Бесселя. Примеры граффиков функции Бесселя приведены на (Рис.24) рассчитываются корни функции Бесселя. Примеры граффиков функции Бесселя приведены на (Рис.24)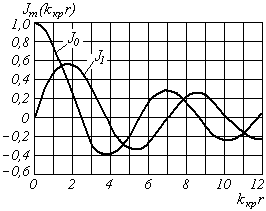 Рис. 24. Функции Бесселя 0-го и 1-го порядка Из графиков на Рис.24 вытекает математический смысл индексов m и n волн 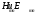 . Индекс m показывает порядок функции Бесселя и определяет число стоячих волн поля укладывающихся вдоль окружности волновода. Индекс n соответсвует номеру корня функции Бесселя и определяет число стоячих полуволн поля укладывающихся вдоль радиуса волновода. . Индекс m показывает порядок функции Бесселя и определяет число стоячих волн поля укладывающихся вдоль окружности волновода. Индекс n соответсвует номеру корня функции Бесселя и определяет число стоячих полуволн поля укладывающихся вдоль радиуса волновода.Волны типа |

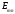 в круглом волноводе.
в круглом волноводе.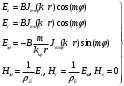
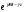 ……… Причем для случая в круглых волновода
……… Причем для случая в круглых волновода 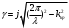 . Граничные условия для волн типа
. Граничные условия для волн типа 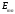 в круглом волноводе определим из общих граничных условий, а именно около проводящей поверхности тангенциальная составляющая электрического поля должна быть равна 0 т.е.
в круглом волноводе определим из общих граничных условий, а именно около проводящей поверхности тангенциальная составляющая электрического поля должна быть равна 0 т.е. 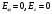 . Критерием простейшей волны в волноводе является не обращение в 0 продольной составляющей а именно
. Критерием простейшей волны в волноводе является не обращение в 0 продольной составляющей а именно 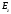 для данного случая. Из выражения 44 следует, что простейшими волнами в круглом волноводе могут быть волны типа
для данного случая. Из выражения 44 следует, что простейшими волнами в круглом волноводе могут быть волны типа 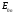 . Согласно граничным условиям при r=a, Ez=0
. Согласно граничным условиям при r=a, Ez=0 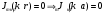 . Для волн типа
. Для волн типа 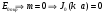
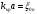 где
где 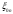 это n-ый корень функции Бесселя нулевого порядка. Таким образом критическое волновое число будет равно
это n-ый корень функции Бесселя нулевого порядка. Таким образом критическое волновое число будет равно 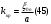 . С учетом выражения 43 найдем критическую длину волны.
. С учетом выражения 43 найдем критическую длину волны.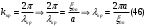 . Как видно из графиков функции Бесселя Рис.24 наименьшее значение корня
. Как видно из графиков функции Бесселя Рис.24 наименьшее значение корня 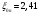 , таким образом из волн типа
, таким образом из волн типа 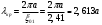 обладает волна
обладает волна 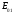 . Для волн
. Для волн 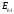 составляющие поля будут определятся выражениями:
составляющие поля будут определятся выражениями: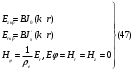
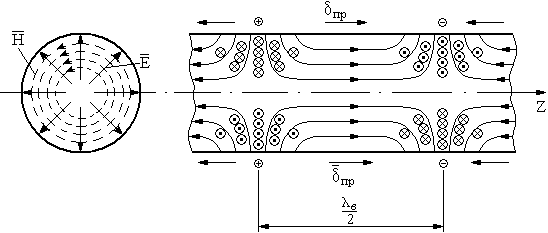
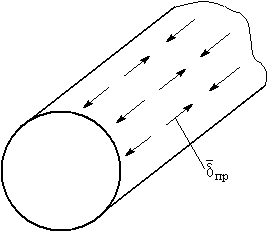
 т.е. продольные токи.
т.е. продольные токи.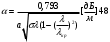 . Предельная мощность пропускаемая волноводом с волной
. Предельная мощность пропускаемая волноводом с волной 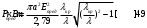 допустимая передаваяемая мощность определяется из выражения 9.
допустимая передаваяемая мощность определяется из выражения 9.