Алгебра логики. Таблицы истинности. Литература по теме урока Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень учебник для 10 класса М. Бином. Лаборатория знаний, 2017 (с. 174197)
 Скачать 111.5 Kb.
|
|
Тема — Алгебра логики. Таблицы истинности Перечень вопросов, рассматриваемых в теме: высказывание, логическая переменная, логические операции (отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция), логические выражения, предикаты и их множества истинности, таблицы истинности и их анализ. Глоссарий по теме: импликация, эквиваленция, предикат, примеры законов алгебры логики. Основная литература по теме урока: Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2017 (с.174—197) Открытые электронные ресурсы по теме: http://lbz.ru/metodist/authors/informatika/3/eor10.php http://kpolyakov.spb.ru/school/ege.htm Теоретический материал для самостоятельного изучения: Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними. Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем.Логическое высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, предложение «Джордж Буль — основоположник алгебры логики» истинно, а «Солнце — спутник Земли» ложно. Употребляемые в обычной речи логические связки «не», «и», «или», «если…то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным. Например, из двух простых высказываний (каких?) можно получить следующее составное высказывание: «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач». Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями). Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С). Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь». Для логических значений «истина» — «ложь» могут использоваться следующие обозначения: И — Л, true — false, да — нет, 1 — 0. Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний. В алгебре логики имеется шесть логических операций. Из курса информатики 8—9 классов вам знакомы три из них: — отрицание (инверсия, логическое НЕ) Высказыванию ставится в соответствие новое высказывание, значение которого противоположно исходному.  — конъюнкция (логическое умножение, логическое И) Высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.  — дизъюнкция (логическое сложение, логическое ИЛИ) Высказывание ложно тогда и только тогда, когда ложны оба исходных высказывания.  Рассмотрим новые логические операции. — Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией (от лат. implicatio — сплетение, тесная связь) или логическим следованием. Операция импликации обозначается символом  и задается следующей таблицей истинности: В разговорной речи импликации соответствуют предложения, содержащие связку «если…, то». Как правило, эту связку мы используем, когда хотим показать зависимость одного события от другого. Импликацию можно заменить на выражение, использующее ранее изученные операции НЕ и ИЛИ:  — Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией. Строгая дизъюнкция обозначается символом  и задается следующей таблицей истинности: В русском языке строгой дизъюнкции соответствует связка «либо». Например, в пословице «Либо пан, либо пропал», выполнение обоих условий одновременно невозможно. В отличие от обычной дизъюнкции в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдет только одно событие. Строгую дизъюнкцию можно представить через базовые операции следующим образом:  Чтобы доказать это равенство, достаточно для всех возможных комбинаций  и  вычислить значения выражения, стоящего в правой части равенства, и сравнить их со значениями выражения  для тех же исходных данных.— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью. В логике эквиваленция обозначается символом  и задается следующей таблицей истинности: В разговорной речи эквивалентности соответствует связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно». Если посмотреть внимательно на таблицы истинности для двух последних логических операций, то можно заметить, что эквивалентность — это обратная операция для операции «исключающее ИЛИ», т. е.  Можно заменить эквивалентность выражением, которое включает только базовые логические операции:  Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок. Для логического выражения справедливо: всякая логическая переменная, а также логические константы (0,1) есть логическое выражение; если  — логическое выражение, то и  — логическое выражение;если A и B — выражения, то связанные любой бинарной операцией, они также представляют собой логическое выражение. При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом: отрицание; конъюнкция; дизъюнкция, строгая дизъюнкция; импликация, эквиваленция. Операции одного приоритета выполняются в порядке их следования, слева направо. Как в математике, скобки меняют порядок выполнения операций. Пример 1. Дан фрагмент таблицы истинности выражения F.
Какое выражение соответствует F? 1) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8 2) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8 3) ¬(x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8 4) (x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8 Решение: обратим внимание, что среди значений функции только одна единица, как у операции «И», поэтому ищем правильный ответ среди вариантов, содержащих «И», «НЕ» и импликацию (варианты 1 и 3) вариант 1 не подходит, потому что при x6=0 в третьей строке получаем 0, а не 1 вариант 3 подходит во всех строчках но давайте убедимся, что варианты 2 и 4 неправильные: — вариант 2 исключаем, потому что при x4=1 во второй строке получаем 1, а не 0 — вариант 4 исключаем, потому что при x5=1 в первой строке получаем 1, а не 0 Ответ: 3 Пример 2. Сколько различных решений имеет уравнение ((K L) → (L M N)) = 0 где K, L, M, N — логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов. Решение Вариант 1 (разделение на части): — из таблицы истинности операции «импликация» следует, что это равенство верно тогда и только тогда, когда одновременно K ˅ L = 1 и L M N = 0 — дизъюнкция ложна, только если обе переменные равны 0, поэтому для первого уравнения рассмотрим три случая: - если K = 1 и L = 0, то второе равенство выполняется при любых М и N; поскольку существует 4 комбинации двух логических переменных (00, 01, 10 и 11), имеем 4 разных решения; - если K = 1 и L = 1, то второе равенство выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения; - если K = 0, то обязательно L = 1 (из первого уравнения); при этом второе равенство выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения; — таким образом, всего получаем 4 + 3 + 3 = 10 решений. Вариант 2 (составление таблицы истинности, достаточно трудоемкий способ): — выражение X = ((K L) → (L M N)) зависит от четырех переменных, поэтому в таблице будет 24 = 16 строчек
— в последнем столбце 10 нулей; это значит, что есть 10 разных комбинаций, при которых выражение X равно нулю, то есть исходное уравнение имеет 10 решений. Ответ: 10 решений Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х<12 становится истинным высказыванием при х=5 и ложным при х=15. Предложения такого рода называют высказывательными формами или предикатами. Предикат — это утверждение, содержащее одну или несколько переменных. Предикаты позволяют задать множество, не перечисляя всех его элементов. Например, множество истинности предиката P(x)=(x<0) — множество отрицательных чисел; множество истинности предиката P(x,y)=(x2+y2=1) – множество точек окружности единичного радиуса в центре в начале координат. Пример 3. Рассмотрим предикат (50 < X·X) → (50 > (X+1)·(X+1)), определенный на множестве целых чисел. Найдем наибольшее число из множества истинности этого предиката. Решение: — задана операция импликации между двумя отношениями  и , решим неравенства — обозначим эти области на оси X: 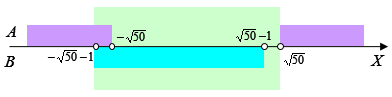 на рисунке фиолетовые зоны обозначают область, где истинно выражение A, голубая зона — это область, где истинно B — исходя из таблицы истинности операции «импликация», заданное выражение истинно везде, кроме областей, где A = 1 и B = 0; область истинности выделена зеленым цветом — поэтому наибольшее целое число, удовлетворяющее условию — это первое целое число, меньшее  , то есть, 7Ответ: 7 |