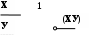лекционный материал. Логические элементы компьютера
 Скачать 134.72 Kb.
|
4. Логические основы ЭВМ. Базовые логические элементы.Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”. Из этого следует два вывода: Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных; На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера. Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Базовыми логическими элементами компьютеров для реализации логических функций являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ (называемые также вентилями). С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от одного до восьми входов и один или два выхода. Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”). Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов также описывают с помощью таблиц истинности. И (конъюнктор)Схема И реализует конъюнкцию двух или более логических значений.
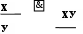 Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x . y Операция конъюнкции на структурных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and. ИЛИ (дизъюнктор)Схема ИЛИ реализует дизъюнкцию двух или более логических значений.
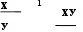 Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица. Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y Знак "1" на схеме — от устаревшего обозначения дизъюнкции как ">=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). НЕ (инвертор)Схема НЕ реализует операцию отрицания (инверсию). |
| x | х |
| 0 | 1 |
| 1 | 0 |
Связь между входом x этой схемы и выходом z можно записать соотношением z = х (читается как "не x" или "инверсия х").
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0.
И—НЕ (элемент Шеффера)
| x | y | (x . y) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И.
Связь между выходом z и входами x и y схемы записывают следующим образом: z = (x . y), где x . y читается как "инверсия x и y".
ИЛИ—НЕ (элемент Пирса)
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.
Связь между выходом z и входами x и y схемы записывают следующим образом: z = (x y), (читается как "инверсия x или y ").
| x | y | (x y) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Пример:
Построить схему, реализующую данную функцию:
F(a, b, c) = a · (b c) ( b · c)
Р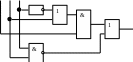
ешение: а в с
F(a, в, c)
Упражнение:
Упростите логические формулы и постройте соответствующие им схемы:
F = a · (b c) a · b a · c
F = ( a · b a · (b c)
F = (a b c) · ( a b c) · (a b c)
F = a · ( b c) (a e · d) · ( a b · c)
F = a · b · c a · b · c a · b · c · d
F = a a · (b c) ( a d g) · (b d) · (c d g · h)