лекционный материал. Логические элементы компьютера

• Название: Логические элементы компьютера
• Дата: 03.10.2022
• Размер: 134.72 Kb.
• Имя файла: лекционный материал.docx
• Тип: Закон; #711623
• страница: 5 из 5

5. Логические элементы компьютера. Триггер и сумматор.

Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю
Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.

Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс).

S Q

R  Q

Он имеет два симметричных входа S и R и два симметричных выхода Q и  Q, причем выходной сигнал Q является логическим отрицанием сигнала Q.

На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов.

Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.

Реализация триггера с помощью вентилей ИЛИ—НЕ и соответствующая таблица истинности.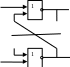

S	R	Q	 Q
0	0	запрещено
0	1	1	0
1	0	0	1
1	1	хранение бита

S Q

R  Q

Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ—НЕ

1. 
   Если на входы триггера подать S=“1”, R=“0”, то (независимо от состояния) на выходе Q верхнего вентиля появится “0”. После этого на входах нижнего вентиля окажется R=“0”, Q=“0” и выход  Q станет равным “1”.
   
2. 
   Точно так же при подаче “0” на вход S и “1” на вход R на выходе  Q появится “0”, а на Q — “1”.
   
3. 
   Если на входы R и S подана логическая “1”, то состояние Q и  Q не меняется.
   
4. 
   Подача на оба входа R и S логического “0” может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.
   

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 2¹⁰ = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

В целях максимального упрощения работы компьютера все многообразие математических операций сводится к сложению двоичных чисел.

Вспомним, что при сложении двоичных чисел образуется сумма в данном разряде, а также возможен перенос в старший разряд.

Слагаемые		Перенос	Сумма
A	B	P	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Из этой таблицы видно, что перенос реализуется с помощью логического элемента «И».

Ч то касается суммы, то наиболее подходящим логическим элементом является элемент «ИЛИ». Однако при сложении четвертой пары чисел в результате должен получаться 0, а не 1. Для того чтобы достичь необходимого результата, можно подать сигнал переноса на логический элемент «НЕ», а затем с его выхода и выхода элемента «ИЛИ» подать сигнал на элемент «И». На выходе элемента «И» мы получим требуемый сигнал.

A (0,0,1,1) P (0,0,0,1)

B(0,1,0,1)

0,0,0,1 1,1,1,0 S(0,1,1,0)

0,1,1,1

Данная схема называется полусумматором, т.к. реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.

Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел

Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.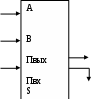

a_i

b_i

p_i

p_i-1

c_i

При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:

1. цифра a_i первого слагаемого;

2. цифра b_i второго слагаемого;

3. перенос p_i–1 из младшего разряда.

В результате сложения получаются две цифры: цифра c_i для суммы; перенос p_i из данного разряда в старший.

Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:

Входы				Выходы
Первое слагаемое	Второе слагаемое	Перенос	Сумма		Перенос
ai	bi	pi-1	ci		pi
0	0	0	0		0
0	0	1	1		0
0	1	0	1		0
0	1	1	0		1
1	0	0	1		0
1	0	1	0		1
1	1	0	0		1
1	1	1	1		1

Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.

Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров.

Например, схема вычисления суммы C = (с₃ c₂ c₁ c₀) двух двоичных трехразрядных чисел A = (a₂ a₁ a₀) и B = (b₂ b₁ b₀), где с₀ – младший разряд суммы, с₃ – старший разряд суммы, может иметь вид: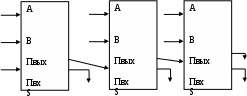




a₀ a₁ a₂
b₀ b₁ b₂

0 с₃
с₀ с₁ с₂

Таким образом, можно сделать вывод, что логические элементы являются строительными «кирпичиками», из которых путем конструирования логических схем строится «здание» любого современного компьютера.

Вопросы для самоконтроля:

1. 
   Что изучает логика, математическая логика, алгебра логики?
   
2. 
   Дайте определение следующих понятий: высказывание, утверждение, рассуждение, умозаключение, логическое выражение.
   
3. 
   Основные логические связки, элементарное и составное высказывания.
   
4. 
   Перечислите основные логические операции и способы их записи.
   
5. 
   Дайте определение логической формулы.
   
6. 
   Объясните смысл следующих понятий: выполнимая логическая формула, тавтология, противоречие, равносильное преобразование формулы.
   
7. 
   Запишите формулы замены импликации и эквиваленции на комбинацию остальных основных логических операций.
   
8. 
   Понятие таблицы истинности логической формулы. Таблицы истинности элементарных формул.
   
9. 
   Что такое упрощение формулы?
   
10. 
    Основные законы алгебры логики.
    
11. 
    Перечислите и охарактеризуйте основные способы решения логических задач.
    
12. 
    Дайте определение логической функции.
    
13. 
    Понятие эквивалентных логических функций.
    
14. 
    Правило построения логической функции по таблицам истинности.
    
15. 
    Определение логического элемента компьютера. Базовые логические элементы.
    
16. 
    Триггер и сумматор. Соответствующие таблицы истинности и логические схемы.