Вариант. Документ Microsoft Word. Лось, хомяк, косуля, кенгуру, капибара, бинтуронг, гиппопотам животные

• Название: Лось, хомяк, косуля, кенгуру, капибара, бинтуронг, гиппопотам животные
• Анкор: Вариант
• Дата: 06.03.2021
• Размер: 72.83 Kb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Документы; #182398

1. Задание В одной из кодировок UTF-16 каждый символ кодируется 16 битами. Гриша написал текст (в нём нет лишних пробелов):

 

«Лось, хомяк, косуля, кенгуру, капибара, бинтуронг, гиппопотам — животные».

 

Ученик вычеркнул из списка название одного из животных. Заодно он вычеркнул ставшие лишними запятые и пробелы — два пробела не должны идти подряд.

При этом размер нового предложения в данной кодировке оказался на 22 байта меньше, чем размер исходного предложения. Напишите в ответе вычеркнутое название животного.

2. Задание Валя шиф­ру­ет рус­ские слова (последовательности букв), за­пи­сы­вая вме­сто каж­дой буквы её код:

А	Д	К	Н	О	С
01	100	101	10	111	000

Некоторые це­поч­ки можно рас­шиф­ро­вать не одним способом. Например, 00010101 может озна­чать не толь­ко СКА, но и СНК. Даны три ко­до­вые цепочки:

100101000

101111100

100111101

 Найдите среди них ту, ко­то­рая имеет толь­ко одну расшифровку, и за­пи­ши­те в от­ве­те рас­шиф­ро­ван­ное слово.

3. Задание Напишите наибольшее целое число x, для которого истинно высказывание:

 

НЕ (X чётное) И НЕ (X >= 7).

 

4. ЗаданиеМежду населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны дороги, протяжённость ко­то­рых (в километрах) при­ве­де­на в таблице: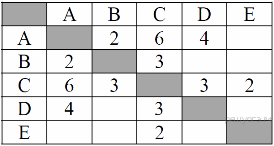



 

Определите длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по дорогам, протяжённость ко­то­рых указана в таблице.

5. Задание У исполнителя Омега две команды, которым присвоены номера:

1. прибавь 4;

2. раздели на b

(b — неизвестное натуральное число; b ≥ 2).

Выполняя первую из них, Омега увеличивает число на экране на 4, а выполняя вторую, делит это число на b. Программа для исполнителя Омега — это последовательность номеров команд. Известно, что программа 12111 переводит число 41 в число 17. Определите значение b.

6. Задание Ниже приведена программа, записанная на пяти языках программирования.

 

Паскаль	Алгоритмический язык
var s, t: integer; begin     readln(s);     readln(t);     if (s > 8) and (t > 8)         then writeln('ДА')         else writeln('НЕТ') end.	алг нач цел s, t ввод s ввод t если s > 8 и t > 8     то вывод "ДА"     иначе вывод "НЕТ" все кон

 

Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:

 

(9, 10); (11, 5); (–2, 8); (9, 9); (2, 8); (–1, 3); (–4, 5); (10, 9); (4, –3).

 

Сколько было запусков, при которых программа напечатала «НЕТ»?

7. Задание

Почтовый ящик teacher находится на сервере shkola1.mos.ru. В таблице фрагменты адреса электронной почты закодированы цифрами от 1 до 6. Запишите последовательность цифр, кодирующую этот адрес.

 

1) @

2) .ru

3) shkola1

4) .

5) teacher

6) mos

8. Задание

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

 

Запрос	Количество страниц (тыс.)
фрегат & эсминец	500
фрегат | эсминец	4500
эсминец	2500

 

Сколько страниц (в тысячах) будет найдено по запросу фрегат?

9. Задание На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город П, проходящих через город Н?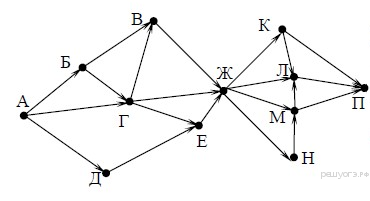



10. Задание

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

 

14₁₆, 17₈, 10011₂.

Задание 1 № 10857 тип 1 (решено неверно или не решено)

Решение.

Поскольку один символ кодируется двумя байтами, из текста удалили 11 символов. Заметим, что лишние запятая и пробел занимают четыре байта. Значит, название животного, которое удалили из списка, должно состоять из девяти букв, поскольку (22 − 4) : 2 = 9 символов. Из всего списка только одно название животного состоит из 9 букв — бинтуронг.

 

Ответ: бинтуронг.


Ваш ответ: нет ответа. Правильный ответ: бинтуронг
Дополнительно

↑ Задание 2 № 27 тип 2 (решено неверно или не решено)

Решение.

Проанализируем каж­дый ва­ри­ант ответа:

 

1) «100101000» может озна­чать как «ДКС» так и «НААС».

2) «101111100» может озна­чать толь­ко «КОД».

3) «100111101» может озна­чать как «ДОК» так и «НАОА».

 

Следовательно, ответ «КОД».


Ваш ответ: нет ответа. Правильный ответ: КОД
Дополнительно

↑ Задание 3 № 10643 тип 3 (решено неверно или не решено)

Решение.

Логическое «И» ложно тогда, когда ложно одно из высказываний. За­пи­шем выражение в виде

 

(X нечётное) И (X < 7).

 

Значит, наибольшее число, для которого высказывание будет истинным — 5.

 

Ответ: 5.


Ваш ответ: нет ответа. Правильный ответ: 5
Дополнительно

↑ Задание 4 № 203 тип 4 (решено неверно или не решено)

Решение.

Найдём все ва­ри­ан­ты маршрутов из A в E и вы­бе­рем самый короткий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пунк­ты D, E.

 

A—B—C—E: длина марш­ру­та 7 км.

A—С—E: длина марш­ру­та 8 км.

A—D—C—E: длина марш­ру­та 9 км.

 

Самый ко­рот­кий путь: A—B—C—E. Длина марш­ру­та 7 км.

 

Ответ: 7.


Ваш ответ: нет ответа. Правильный ответ: 7
Дополнительно

↑ Задание 5 № 10885 тип 5 (решено неверно или не решено)  

 

Ответ: 9.

↑ Задание 6 № 10470 тип 6 (решено неверно или не решено)

Решение.

Заметим, что программа напечатает «НЕТ», если одна из введённых переменных s и t будет меньше или равна 8. Значит, было 6 запусков, при которых программа напечатала «НЕТ». В качестве значений переменных s и t в этих случаях вводились следующие пары чисел:

 

(11, 5); (–2, 8); (2, 8); (–1, 3); (–4, 5); (4, –3).

 

Ответ: 6.

↑ Задание 7 № 5276 тип 7 (решено неверно или не решено)

Решение.

Напомним, как формируется почтовый адрес в сети Интернет. Сначала указывается имя почтового ящика, потом «@», потом сервер, на котором находится почтовый ящик. Таким образом, искомый адрес будет следующим: [e-mail].

 Ответ: 513462.


↑ Задание 8 № 10488 тип 8 (решено неверно или не решено)

Решение.

По формуле включений и исключений имеем:

 

m(фрегат | эсминец) = m(фрегат) + m(эсминец) − m(фрегат & эсминец) =

= m(фрегат) + 2500 − 500 = 4500.

 

Откуда получаем, что m(фрегат) = 4500 − 2500 + 500 = 2500.

↑ Задание 9 № 11017 тип 9 (решено неверно или не решено)

А = 1

Б = А = 1

Д = А = 1

Г = А + Б = 1 + 1 = 2

В = Б + Г = 1 + 2 = 3

Е = Г + Д = 2 + 1 = 3

Ж = В + Г + Е = 3 + 2 + 3 = 8

Н = Ж = 8

М = Н = 8 (так как ищем пути проходящие через город Н)

Л = М = 8

П = Л + М = 16.

↑ Задание 10 № 10333 тип 10 (решено неверно или не решено)

Решение.

Переведём все числа в десятичную систему счисления:

1. 14₁₆ = 20₁₀;

2. 17₈ = 15₁₀;

3. 10011₂ = 19₁₀.

Таким образом, наименьшим среди этих трёх чисел является число 15.

 

Ответ: 15.