ЛР № 1
Распознавание типов формальных языков и грамматик
Цели работы:
- закрепить понятия «алфавит», «цепочка», «формальная грамматика», «формальный язык», «выводимость цепочек», «эквивалентная грамматика»;
- сформировать умения и навыки распознавания типов формальных языков и грамматик по классификации Хомского, построения эквивалентных грамматик.
Постановка задачи к работе № 1
При выполнении работы следует реализовать следующие действия:
1) составить несколько грамматик (по возможности разных типов), порождающих формальный язык, заданный в соответствии с вариантом;
2) определить тип формальных грамматик и языка по классификации Хомского;
3) привести примеры вывода нескольких цепочек в соответствии с правилами грамматик.
Варианты индивидуальных заданий представлены в таблице 1.
Таблица 1 − Варианты индивидуальных заданий к работе №1.
Вариант Формальный язык
1 L(G)={anbmck| n, m, k>0}
2 L(G)={(ab)n(cb)m| n, m0}
3 L(G)={0n(10)m| n, m0}
4 L(G)={wcwcw | w{a, b}+}
5 L(G)={c2ndn| n>0}
6 L(G)={l+l-l | l {a, b}+}
7 L(G)={(10)n-1(01)n+1 | n>0}
8 L(G)={(ac)n| n>0, a{b, d}, c{+, -}}
9 L(G)={(010)n | n>0}
10 L(G)={a1a2…anan…a2a1 | ai{0, 1}}
11 L(G)={a1a2…ana1a2…an | ai{c, d}}
12 L(G)={ab.b | ai{+, -}, b
ЛР № 2.
Построение конечного автомата по регулярной грамматике
Цели работы:
- закрепить понятия «регулярная грамматика», «недетерминированный и детерминированный конечный автомат»;
- сформировать умения и навыки построения конечного автомата по регулярной грамматике и преобразования недетерминированного конечного автомата к детерминированному конечному автомату.
Постановка задачи к работе № 2
При выполнении работы реализовать следующие действия:
1) выполнить проверку заданной грамматики на принадлежность к классу регулярных грамматик;
2) построить по заданной регулярной грамматике конечный автомат;
3) преобразовать недетерминированный конечный автомат к детерминированному конечному автомату;
4) построить графы получившихся конечных автоматов.
Варианты индивидуального задания представлены в таблице 2.
Таблица 2 − Варианты индивидуального задания к работе № 2
Вариант Регулярная грамматика
1 G=({S, C, D}, {0, 1}, P, S), где P:
1) S1C | 0D; 2) C0D | 0S | 1; 3) D1C | 1S | 0.
2 G=({S, A, B, C}, {a, b, c}, P, S), где P:
1) SaA | bB | aC; 2) AbA | bB | c; 3) BaA | cC | b; 4) CbB | bC |a.
3 G=({K, L, M, N}, {a, b, +, -, }, P, K), где P:
1) KaL | bM; 2) L-N | -M; 3) M+N; 4) NaL | bM | .
4 G=({X, Y, Z, W, V}, {0, 1, , #, &}, P, X), где P:
1) X0Y | 1Z | ; 2) Y0Z |
W | #; 3) Z1Y | 1W | 0V;
4) W0W | 1W | #; 5) V&Z.
5 G=({K, L, M, N, Q, P, R, S}, {0, 1, *, $, /}, V, K), где V:
1) K1L | 0N; 2) L0M | 0P | /Q; 3) N1R | 1M | *S; 4) Q1P;
5) P*L | $; 6) M$; 7) S0R; 8) R/N | $.
6 G=({E, A, B, C, D}, {0, 1, a, b, c}, P, E), где P:
1) E0A | ; 2) AaB | aD; 3) BbB | 1C | c; 4) DaD | 0C | c.
7 G=({X, Y, Z, V, W}, {0, 1, x, y, z}, P, X), где P:
1) XyY | zZ; 2) Y1V; 3) Z0W | 0Y; 4) VxZ | xW | 1; 5) W1Y | 0.
8 G=({S, A, B, C, D}, {a, b, c, d, }, P, S), где P:
1) SaA | bB; 2) AcC | ; 3) CcC | cA; 4) BdD | ; 5) DdD |dB.
9 G=({K, L, M, N, P}, {0, 1, &, %, a, b}, C, K), где C:
1) K1M | ; 2) M0L | &N | &P; 3) L1L | 0L | %P;
4) NaN | bN | %P; 5) P1P | aP | 0.
10 G=({I, J, K, M, N}, {0, 1,
, !}, P, I), где P:
1) I0J | 1K | 0M; 2) J
K | 0M; 3) K
M | 0J | 0N; 4) M1K | !;
5) N0I | 1I | !.
11 G=({S, A, B, C, D, E}, {a, b, c, d, e, $, }, P, S), где P:
1) SaA | bB | cC; 2) AdD; 3) B#D | $E; 4) DdD | dB | ;
5) CcE; 6) EeE | eB | .
12 G=({X, Y, Z, V}, {(, ), y, z, v}, P, X), где P:
1) X(Y | ; 2) YyY | zY | zZ; 3) ZzZ | vZ | vV; 4) VvV |).
ЛР № 3.
Минимизация конечных автоматов
Цели работы:
- закрепить понятия «недостижимые состояния автомата», «эквивалентные состояния автомата», «минимальный конечный автомат»;
- сформировать умения и навыки минимизации детерминированного конечного автомата.
Постановка задачи к работе № 3
При выполнении работы реализовать следующие действия:
1) устранить недостижимые состояния конечного автомата;
2) исключить эквивалентные состояния конечного автомата;
3) построить граф минимального конечного автомата;
4) разработать серию контрольных примеров и провести тестирование КА.
Варианты индивидуальных заданий к работе № 3 представлены на рисунке.
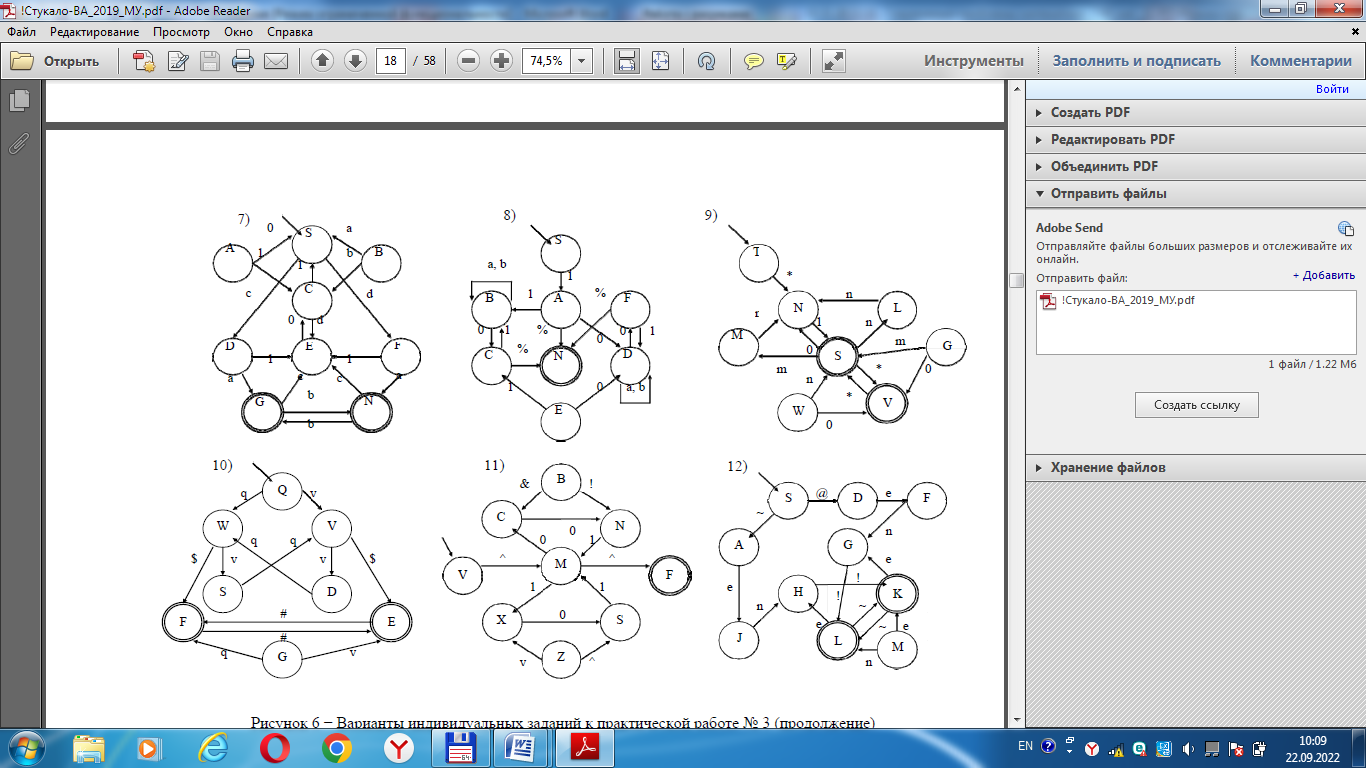 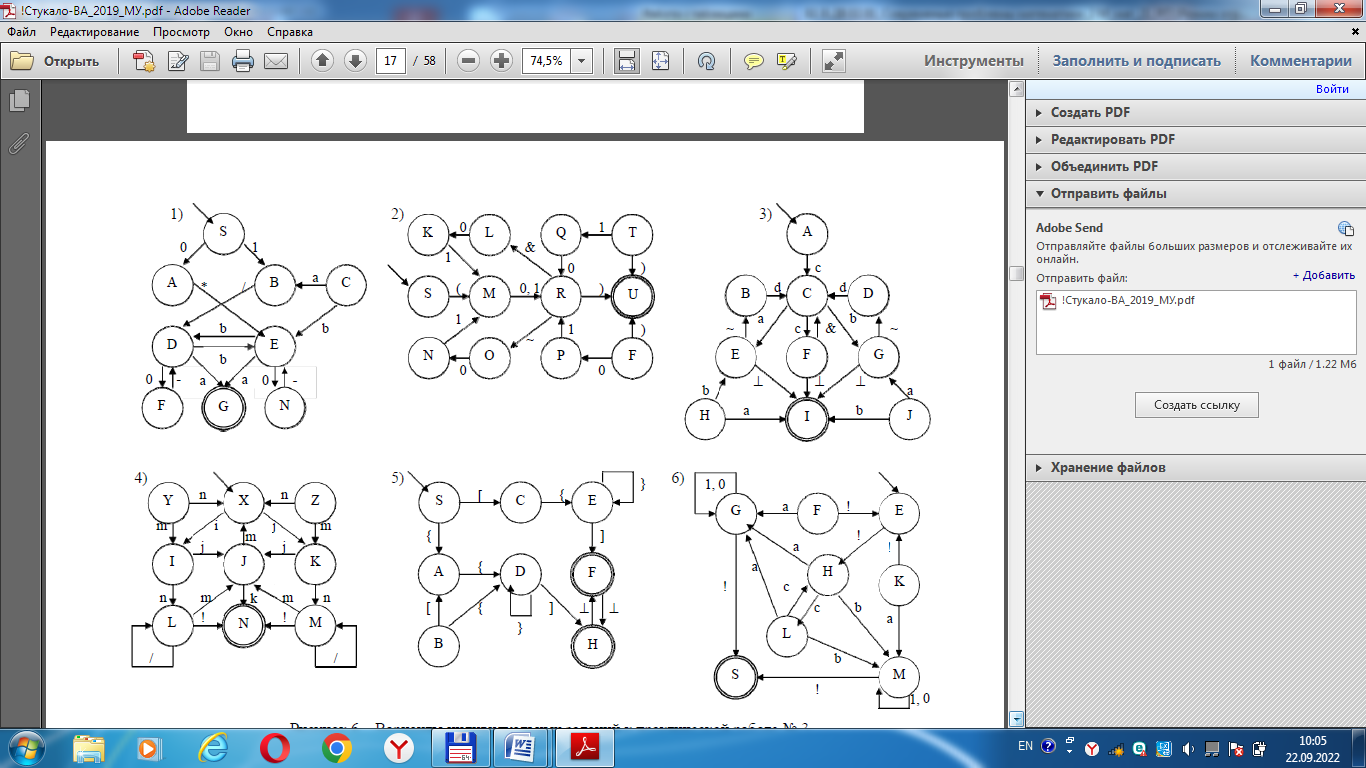
ЛР № 4
Эквивалентные преобразования контекстно-свободных грамматик
Цели работы:
- закрепить понятия «эквивалентные грамматики», «приведенная КС-
грамматика»;
- сформировать умения и навыки эквивалентных преобразований контекстно-свободных грамматик.
Постановка задачи к работе № 4
При выполнении работы следует реализовать следующие действия:
1 проверить грамматику на принадлежность к классу КС-грамматик;
2 проверить существование языка КС-грамматики;
3 выполнить эквивалентные преобразования грамматики, направленные
на удаление:
а) бесполезных символов;
б) недостижимых символов;
в) ε-правил;
г) цепных правил;
д) левой факторизации правил;
е) прямой левой рекурсии.
Варианты индивидуальных заданий представлены в таблице 9
Варианты индивидуальных заданий к работам № 4 и 5
1
G=({S, A, B, D, E},{a, b, c, e}, P, S), где P:
1) SAB | ε; 2) AAa | S | a; 3) BbD | bS | b; 4) DccD;
5) EeE |e
25
2
G=({E, T, F, G, H}, {+, -, *, /, n, m, h}, P, E), где P:
1) ET | E+T | E-T | ε; 2) TF | F*T | F/T | ε;
3) FG | Fn | n; 4) GGm; 5) HHh | h
3
G=({S, R, T, X, Y}, {a, b, p, g, y}, P, S), где P:
1) S R | T; 2) R pX | paR | paT| ε; 3) T Tg | g;
4) XaXb; 5) Y aYa | y
4
G=({Q, A, B, C, D}, {a, b, c, d}, P, Q), где P:
1) Q acA | acB | ε; 2) B A | Cb | ε; 3) A Aa | Ab | a;
4) C dCc; 5) D dc
5
G=({R, T, F, G, K}, {m, i, j, k, ^,
, }, P, R), где P:
1) RR
T | R^T |ε; 2) TF | Fi | Fj | Gk | ε;
3) GGkG; 4) KKi | Km | m
6
G=({S, X, Y, Z, K}, {x, y, z, k, #, $}, P, S), где P:
1) SX | Y | Z; 2) Xx#X | x#Y | ε; 3) YYy$ |Yz$ | $ |ε;
4) ZZz$; 5) KKk$ | k$
7
G=({S, L, M, P, N}, {n, m, l, p, @, }, V, S), где V:
1) S@nL | @mM | P; 2) LM | Ll | Lm |ε;
3) ML | Mm | mm; 4) NpN@ | @; 5) PnmP
8
G=({X, Y, Z, K, L}, {a, b, l, =, <, >, , , }, V, X), где V:
1) XY | Y=Y | Y<Y | Y>Y | K; 2) YYZ | Y Z | ε;
3) Z __________a | b | ε; 4) K K; 5) L l | a | b
9
G=({Q, A, B, C, D}, {0, 1, -}, P, Q), где P:
1) Q01A | 01B | A; 2) A 0B1 | B | 1 | ε; 3) BBA0 | B1 | C | ε;
4) C0C11; 5) D - D1 | -0 | -1
10
G=({R, T, U, W, V}, {0, 1, +, -, *, /}, P, R), где P:
1) RT1T | T1U | W | ε; 2) TU | T01 | T10 |ε;
3) U+U | +0 | +1; 4) WW-W | W+W; 5) V*0 | /1
11
G=({S, R, T, F, E}, {a, b, k, {, [, }, ], }, P, S), где P:
1) S{R | [ R; 2) RRa} | Ra] | a | T | F | ε;
3) F{F} | bb; 4) T[T]; 5) Ek
12
G=({Y, K, M, L, S}, {a, b, *, /, ^}, P, Y), где P:
1) YKS | KM; 2) KK* | K/ | S; 3)SSa/ | Sb/ | ε;
4) M*M*; 5) LL^ | ^a
ЛР № 5
Построение автомата с магазинной памятью по контекстносвободной грамматике
Цели работы:
- закрепить понятия «автомат с магазинной памятью (МП-автомат)»,
«расширенный МП-автомат», «конфигурация МП-автомата»; «строка и язык, допускаемые МП-автоматом»;
- сформировать умения и навыки построения МП-автомата и расширенного МП-автомата по КС-грамматике, разбора входной строки с помощью МП-автомата.
Постановка задачи к работе № 5
При выполнении работы следует реализовать следующие действия:
а) проверить грамматику на принадлежность к классу КС-грамматик;
б) построить МП-автомат по КС-грамматике;
в) построить расширенный МП-автомат по КС-грамматике;
г) продемонстрировать разбор некоторой входной строки с помощью построенных автоматов для случая:
- входная строка принадлежит языку исходной КС-грамматики и допускается МП-автоматом;
- входная строка не принадлежит языку исходной КС-грамматики и не допускается МП-автоматом.
Индивидуальные варианты заданий представлены в ЛР №4.
ЛР № 6
Функционирование распознавателя для LL(1)-грамматик
Цели работы:
- закрепить понятие «LL(k)-грамматика», необходимые и достаточные условия LL(k)-грамматики;
- сформировать умения и навыки построения множеств FIRST(k, ) и
FOLLOW(k, ), распознавателя для LL(1)-грамматик.
Постановка задачи к работе № 6
При выполнении практической работы следует реализовать следующие действия:
- построить множества FIRST(1, A) и FOLLOW(1, A) для каждого нетерминального символа грамматики;
- проверить необходимое и достаточное условия LL(1) для КС-грамматики;
- проиллюстрировать функционирование распознавателя для LL(1)-грамматик, составив набор контрольных примеров для случаев:
а) введенная КС-грамматика не является LL(1)-грамматикой;
б) исходная КС-грамматика является LL(1)-грамматикой, но входная строка не принадлежит языку грамматики;
в) заданная КС-грамматика является LL(1)-грамматикой, и введенная строка принадлежит языку грамматики.
Разбор цепочек показать с помощью таблицы, строки вывода и дерева вывода.
Вариантами индивидуальных заданий к лабораторной работе № 6 являются выходные данные лабораторной работы № 4. |
 Скачать 0.55 Mb.
Скачать 0.55 Mb.

