ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ. 1932_Артамонова_ЛР4_ОТУ. М. С. Брунов должность, уч степень, звание подпись, дата инициалы, фамилия
 Скачать 196.5 Kb. Скачать 196.5 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ» КАФЕДРА №31 ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ_____________________ ПРЕПОДАВАТЕЛЬ
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ № 4 ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ по курсу: Основы теории управления
Санкт-Петербург, 2021 1 Цель работы Изучения основных методов определения устойчивости замкнутых систем по годографу Найквиста. Определение запасов устойчивости по ЛАЧХ и ЛФЧХ. Задание 1: для систем wr1, wr2, wr3, wr4 построить карту полюсов и нулей и диаграмму Найквиста. Исследовать устойчивость исходной (разомкнутой) и соответствующей замкнутой (единичной, отрицательной обратной связью). Результат проверить, построив переходную характеристику замкнутой системы. Задание 2: для системы wr5 построить диаграммы Боде (ЛАЧХ и ЛФЧХ). Исследовать устойчивость исходной (разомкнутой) и соответствующей замкнутой (единичной, отрицательной обратной связью) систем. Определить запасы устойчивости по амплитуде и фазе. 2 Теоретическая часть Устойчивость САУ является одним из основных условий ее работоспособности и включает требование затухания во времени переходных процессов. Система является устойчивой, если при ограниченном входном сигнале её выходной сигнал также является ограниченным. Если система устойчива, то она противостоит внешним воздействиям, а выведенная из состояния равновесия возвращается снова к нему. Система с расходящимся переходным процессом будет неустойчивой и неработоспособной. Условием устойчивости системы является расположение всех полюсов в левой комплексной полуплоскости. Тогда все полюсы будут давать затухающую реакцию. Выше сформулированное условие устойчивости справедливо как для линейных, так и для линеаризованных систем. Однако в случае нулевых или чисто мнимых корней характеристического уравнения вопрос об устойчивости линеаризованной системы может быть решен только на основании исследования ее нелинейных уравнений. Критерии устойчивости разделяют на алгебраические и частотные. В частности, к алгебраическим критериям относится критерий Гурвица, к частотным критерия – критерий Найквиста. Частотный критерий устойчивости Найквиста анализирует АФЧХ разомкнутой системы. Пусть имеется ПФ разомкнутой системы W(jω). Передаточная функция приобретает вид Основные свойства АФЧХ разомкнутой системы: 1. Если разомкнутая система не имеет интегрирующих звеньев, то при ω= 0 ее АФЧХ начинается на вещественной оси в точке P(ω)=K (где K – коэффициент усиления разомкнутой системы). Заканчивается АФЧХ в начале координат при ω→ ∞ (рис. 1, а). 2. Если разомкнутая система имеет одно интегрирующее звено, то ее АФЧХ начинается при ω= 0в бесконечности на отрицательной мнимой полуоси, а заканчивается в начале координат при ω→ ∞ (рис. 1, б).  Рисунок 1 - АФЧХ разомкнутой системы Критерий устойчивости Найквиста формулируется так: 1. Если разомкнутая система устойчива или находится на границе устойчивости, то для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты ω от 0 до ∞ не охватывала точку с координатами –1,j. 2. Если разомкнутая система неустойчива, а ее передаточная функция имеет m полюсов справа от мнимой оси на комплексной плоскости, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от ω от – ∞ до + ∞ охватывала m раз точку с координатами –1, j. При использовании этого критерия нужно учитывать две особенности: 1. Если разомкнутая система находится на границе устойчивости, то ее АФЧХ уходит в бесконечность. Для проверки критерия Найквиста нужно мысленно соединить конец АФЧХ дугой бесконечно большого радиуса с положительной вещественной полуосью. 2. На практике АФЧХ может строиться только для положительных частот (0 ≤ ω < + ∞). При применении критерия Найквиста считается, что ветвь АФЧХ для отрицательных частот симметрична относительно вещественной оси. Для проверки устойчивости САУ по Найквисту сначала нужно выяснить, является ли устойчивой разомкнутая система. 3 Практическая часть 3.1 Критерий Найквиста Для варианта 1: m = 1/100. 3.1.1 Скрипт для системы wr1 будет выглядеть следующим образом: m=1/100 %первые два графика - исследование разомкнутой системы figure (1) subplot(221) wr1=tf([1] , [1 1-m]) %ПФ разомкнутой системы pole(wr1) pzmap(wr1) % Нули полюсы разомкнутой системы subplot(222) step(wr1);grid %диаграмма subplot(223) nyquist(wr1) subplot(224) wr1z=feedback(wr1,1) %ПФ замкнутой системы impulse(wr1z); grid Замкнутая и разомкнутая системы заданы передаточными функциями  Результаты выполнения команды представлены на рисунке 2. 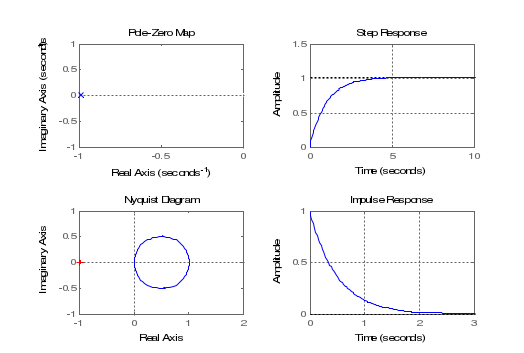 Рисунок 2 - Разомкнутая – устойчива, замкнутая – устойчива Из критерия устойчивости: если разомкнутая система устойчива или находится на границе устойчивости, то для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты ω от 0 до ∞ не охватывала точку, как видно из графика на рисунке 2. Импульсная характеристика затухающая, стремится к 0. 3.1.2 Для системы wr2 аналогично. Замкнутая и разомкнутая системы заданы передаточными функциями 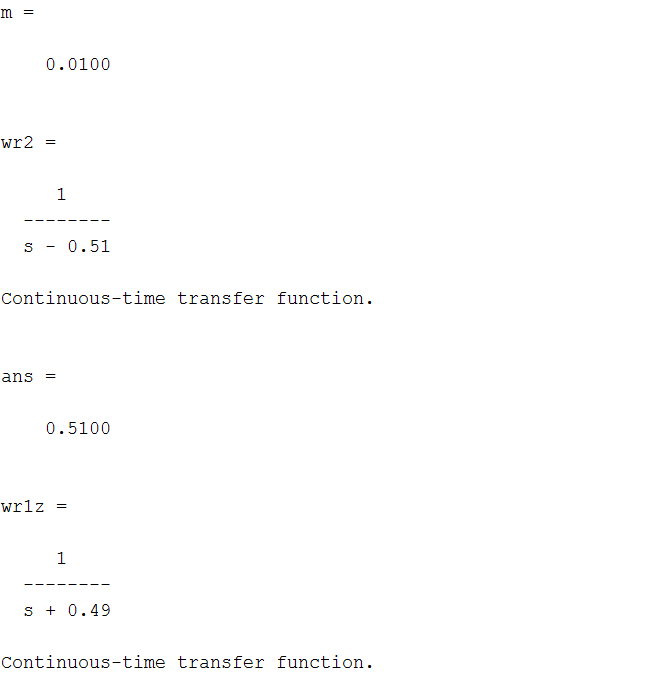 Результаты выполнения команды представлены на рисунке 3.  Рисунок 3 - Разомкнутая – неустойчива, замкнутая – устойчива Полюс справа - система неустойчива. Годограф неустойчивой разомкнутой системы при изменении охватывает точку -1 на оси абсцисс в положительном направлении m/2 раз, значит, что замкнутая система будет устойчивой. Импульсная характеристика затухающая, стремится к 0. 3.1.3 Для системы wr3. Замкнутая и разомкнутая системы заданы передаточными функциями  Результаты выполнения команды представлены на рисунке 4. 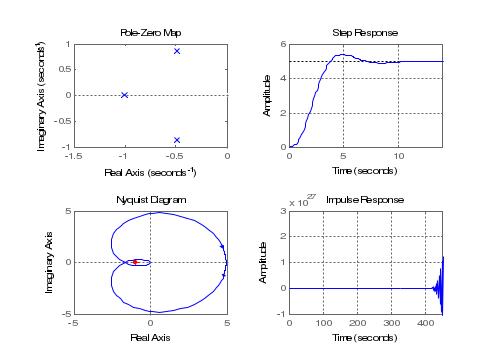 Рисунок 4 - Замкнутая– неустойчива, разомкнутая – устойчива Замкнутая система неустойчива, так как точка -1 охватывается кривой годографа разомкнутой системы, что видно на рисунке 4. Переходная характеристика стремится к постоянному значению. 3.1.4 Аналогично для системы wr4 Замкнутая и разомкнутая системы заданы передаточными функциями 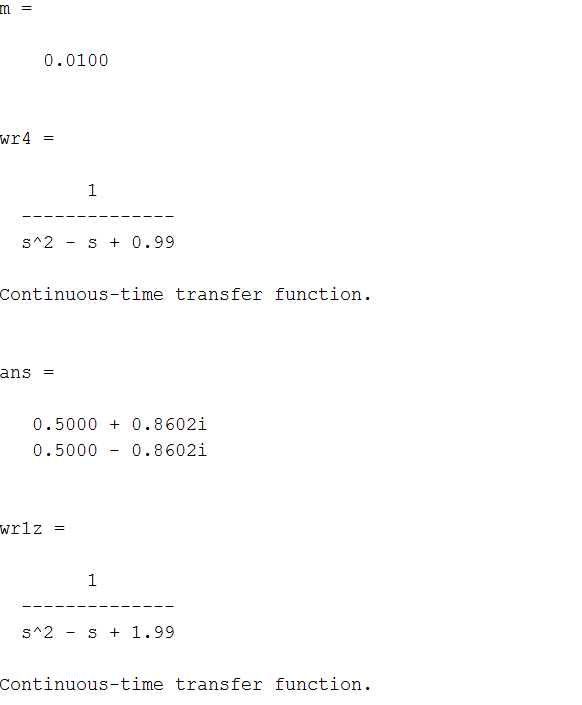 Результаты выполнения команды представлены на рисунке 5. 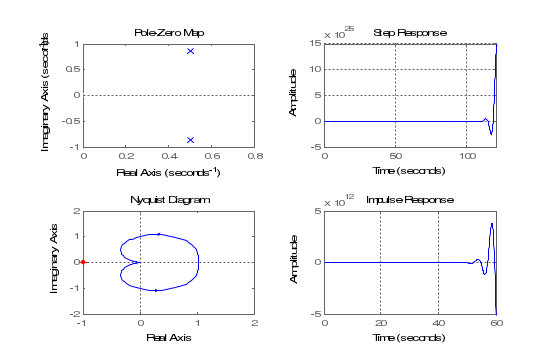 Рисунок 5 - Замкнутая – неустойчива, разомкнутая – неустойчива Годограф неустойчивой разомкнутой системы при изменении не охватывает точку -1 на оси абсцисс. Значит, замкнутая система будет неустойчивой. 3.2 Исследование запаса устойчивости Убедимся, что система минимально-фазовая (все нули и полюсы разомкнутой системы должны находятся в левой полуплоскости комплексной плоскости), запустив скрипт: m=1/100 %figure (5) wr6=tf([1.7+m] , [1 2 3 1]) %полюсы разомкнутой pole(wr6) %итог - все отрицательны w6z=feedback(wr6,1) %полюсы замкнутой pole(w6z) %итог - все отрицательны В командном окне получим значения полюсов:  Нули (корни числителя ПФ) отсутствуют, действительные части всех полюсов (корней знаменателя ПФ) отрицательны. Система минимальнофазовая, и можно применить критерий Найквиста, формулируемый для логарифмических частотных характеристик. Построим диаграммы Боде: %АЧХ и ФЧХ в логарифмическом масштабе bode(wr6); grid Результаты выполнения команды представлены на рисунке 6. 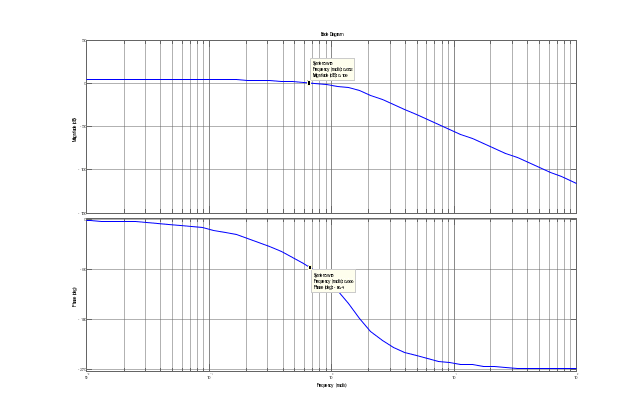 Таким образом, получаем следующие значения для запасов устойчивости: запас по амплитуде: 8.19 дБ; запас по фазе: 86.4 град. Увеличение коэффициента усиление приводит к потере устойчивости замкнутой системы. 4 Вывод В ходе лабораторной работы были изучены основные методы определения устойчивости замкнутых систем по годографу Найквиста: для систем wr1, wr2, wr3, wr4 были карта полюсов и нулей и диаграмма Найквиста, исследована устойчивость исходной (разомкнутой) и соответствующей замкнутой (единичной, отрицательной обратной связью). А также определены запасы устойчивости по ЛАЧХ И ЛФЧХ для системы wr5. | ||||||||||||||||||||||||
